Может ли быть определитель матрицы отрицательным: Определитель матрицы меньше нуля то. Методы вычислений определителей

11. Преобразования определителя не изменяющие его величины.

Определитель не меняется при транспонировании. IAI=IAI стТ. Если один определитель получен из другого перестановкой двух строк, то все члены первого определителя будут членами и во втором, но с обратными знаками, т. е. от перестановки двух строк определитель лишь меняет знак.Определитель не меняется, если к элементам одной из его строк прибавляются соответственные элементы другой строки, умноженные на одно и то же число. Так как число k может быть и отрицательным, то определитель не меняется и при вычитании из одной его строки другой строки, умноженной на некоторое число. Вообще, определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк.

Св-ва определителей:1) Постоянный множитель из элементов какого либо ряда можно выносить за знак определителя. 2) Определитель равен нулю, если все элементы какого-либо

ряда равны нулю.3) Определитель равен нулю, если все элементы какого-либо

ряда равны нулю.

12. Преобразования определителя изменяющие его величину. Если одна из строк определителя состоит из нулей, то определитель равен нулю. Если один определитель получен из другого перестановкой двух строк, то все члены первого определителя будут членами и во втором, но с обратными знаками, т. е. от

перестановки двух строк определитель лишь меняет знак.Определитель, содержащий две одинаковые строки, равен нулю. 5) Если все элементы некоторой строки определителя умножить на некоторое число k,

то сам определитель умножится на k. Определитель, содержащий две пропорциональные строки, равен нулю. Если все элементы i-й строки, определителя n-го порядка представлены в виде, суммы двух слагаемых: aij = bj + cj ,то определитель равен сумме двух определителей, у которых все строки, кроме i-й, — такие же, как и в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом — из элементов cj. 8) Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен нулю.

Определитель не меняется, если к элементам одной из его строк прибавляются

соответственные элементы другой строки, умноженные на одно и то же число. Так как число k может быть и отрицательным, то определитель не меняется и при вычитании из одной его строки другой строки, умноженной на некоторое число. Вообще, определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк.

13. Лемма о миноре. Пусть дан определитель d порядка n. Берем целое число k, удовлетворяющее

условию 1 ≤ k ≤ n — 1, и в определителе d выбираем произвольные k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов, т. е. принадлежащие к одной из выбранных строк и к одному из выбранных столбцов, составляют, очевидно, матрицу порядка k. Определитель этой матрицы называется минором k-го порядка определителя d.

Произведение любого минора М k-го порядка на его алгебраическое

дополнение в определителе d является алгебраической суммой, слагаемые, которой получающиеся от умножения членов минора М на взятые со знаком (-1)^S m члены

дополнительного минора М’, будут некоторыми членами определителя d, причем их знаки

в этой сумме совпадают с теми знаками, с какими они входят в состав определителя. i+j M’.

Утверждение. Определитель d равен сумме произведений всех элементов

произвольной его строки на их алгебраические дополнения. (Аналогичное разложение

определителя можно получить и по любому его столбцу.) d = аi1Аi1 + ai2Ai2 + … + ainAin.

14. Теорема Лапласса. Пусть в определителе d порядка n произвольно выбраны k строк

(или k столбцов), 1 ≤ k ≤ n — 1. Тогда сумма произведений всех миноров k-го порядка,

содержащихся в выбранных строках, на их алгебраические дополнения равна

определителю d.

Число миноров, по которым берётся сумма в теореме Лапласа, равно числу способов выбрать k столбцов из n, то есть биномиальному коэффициенту (n/k) .

Доказательство. Рассмотрим сумму произведений всех элементов произвольной k-ой строки матрицы А на алгебраические дополнения соответствующих элементов любой другой, скажем, i-ой строки матрицы А. Пусть A′ – матрица, у которой все строки, кроме i-ой, такие же, как у матрицы А, а элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матрицы А. Тогда у матрицы A′ две одинаковые строки и, следовательно, по свойству матрицы об одинаковых строках имеем, что |A′| = 0 . С другой стороны, по следствию 1 определитель |A′| равен сумме произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения. Заметим, что алгебраические дополнения элементов i-ой строки матрицы A′ совпадают с алгебраическими дополнениями соответствующих элементов i-ой строки матрицы А. Но элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матри- цы А. Таким образом, сумма произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения с одной стороны равна нулю, а с другой стороны равна сумме произведений всех элементов k-ой строки матрицы А на алгебраические дополнения соответствующих элементов i-ой строки матрицы А.

Так как строки и столбцы матрицы равносильны относительно свойств определителя, теорему Лапласа можно сформулировать и для столбцов матрицы.

15. Разложение определителя по строке или столбцу. Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.

Пусть A = (aij) — квадратная матрица размера n*n . Пусть также задан некоторый номер строки i либо номер столбца j матрицы A. Тогда определитель A может быть вычислен по следующим формулам: разложение по i-ой строке:det A=E(от n до j=1)aijAij. Разложение по j-ому столбцу: detA=E(от n до i=1 )aijAij

, где Aij — алгебраическое дополнение к минору, расположенному в строке с номером i и столбце с номером j. Aij также называют алгебраическим дополнением к элементу aij.

Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить k равным 1 и выбрать i-ую строку, тогда минорами, расположенными в этой строке будут сами элементы.

Следствие 2.Сумма произведений всех элементов некоторой строки (столбца) матрицы А на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.

16. Правило Крамера. Вспомогательным определителем Dj для 1<= j<=n называется пределитель поучаемый из D заменой j-го порядка на столбец свободных членов системы. Справедливы следующие неравенства: biA1j+b2A2j+…+bnAnj=Dj; a1iA1j+a2iA2j+…+anjAnj={ D если i=j,0 в противном случае.

Лемма2.Другими словами эта формула говорит, что сумма произведений элементов столбца определителя алгебраические дополнения элементов другого столбца этого определителя равна нулю , а на свои алгебраические дополнения равна определителю. Аналогично формулируется строчный вариант этой леммы.

Th.Правило Крамера : Если главный опрделитель квадратной СЛАУ отличен от нуля,то эта система имеет единственное решение: x1=D1/D, x=D2/D, . . ., xn=Dn/D.

Метод Крамера требует придлизительно в n раз больше арифметических операций, чем метод Гаусса.

Но в приложениях к дифференциальным уравнениям любят пользоваться этой рядовой теоремой линейной алгебры для формулировки единственности решения некоторых систем дифференциальных уравнений.

Следствие 1:Квадратная однородная СЛАУ имеет ненулевое решение тогда и только тогда , когда главный определитель системы равен нулю.

Определитель — матрица — коэффициент

Cтраница 1

Определитель матрицы коэффициентов этой системы уравнений, составленный из коэффициентов при первых трех неизвестных, отличен от нуля.  [1]

Обратимость предполагает отличный от нуля определитель матрицы коэффициентов.  [2]

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю.

В этом случае соблюдается лишь необходимое, но недостаточное условие идентификации.  [3]

Уравнение для критических сил МГЭ является определителем матрицы коэффициентов решения задачи Коши, который формируется без привлечения сложных аналитических преобразований и не содержит точек разрыва второго рода.  [4]

После ряда нагружений может оказаться, что определитель матрицы коэффициентов cfj окажется равным нулю или, перейдя через нуль, станет отрицательным. Это будет означать, что несущая способность системы превышена.  [5]

Ненулевое решение этой системы существует при обращении определителя матрицы коэффициентов в нуль.  [6]

Любые т переменных системы т линейных уравнений с п неизвестными ( тп) называются основными или базисными, если

определитель матрицы коэффициентов при них не равен нулю.  [7]

Любые т переменных системы / я-линейных уравнений с п неизвестными ( т п) назьюаются основными, или базисными, если определитель матрицы коэффициентов при них не равен нулю. Тогда остальные п — т переменных назьюаются небазисными.  [8]

Аг — определитель, полученный из определителя А заменой его i — ro столбца столбцом свободных членов системы; А — определитель матрицы коэффициентов системы уравнений; п — число уравнений и неизвестных.  [9]

Докажите, что однородная система линейных уравнений с квадратной матрицей коэффициентов имеет ненулевое ( только нулевое) решение тогда и только тогда, когда определитель матрицы коэффициентов равен ( не равен) нулю.  [10]

Максимального правдоподобия метод ( maximum likelihood): метод статистического оценивания, в котором определяется значение переменных генеральной совокупности с использованием выборочного распределения; в факторном анализе — метод получения первоначального факторного решения, его варианты включают канонический факторный анализ и метод минимизации

определителя матрицы остаточных коэффициентов корреляции.  [11]

Определитель этого графа является определителем матрицы коэффициентов передачи, которая была введена в гл.  [12]

Уравнение лишь тогда имеет одно решение для 71 и 72 когда матрица выплат является обратимой. Обратимость предполагает отличный от нуля определитель матрицы коэффициентов.  [13]

Достаточным условием того, что крайние точки X ( А, Ъ) будут целочисленными при любом целочисленном векторе Ь, является унимодулярность базиса. Пользуясь правилом Крамера, можно решить систему относительно всех xi, и, так как

определитель матрицы коэффициентов, стоящий в знаменателе, равен 1, а Ь имеет целочисленные компоненты, xt должны быть целочисленными. Докажем теперь, что унимодулярность является и необходимым условием.  [14]

Для этого часть неизвестных необходимо зафиксировать. Число фиксируемых неизвестных равно разности между общим числом неизвестных и рангом матрицы. Поскольку фиксируемые переменные могут принимать бесконечное количество значений, система не будет иметь единственного решения. Для того чтобы неоднородная система п уравнений с п неизвестными имела единственное решение, необходимо и достаточно, чтобы определитель матрицы коэффициентов был отличен от нуля.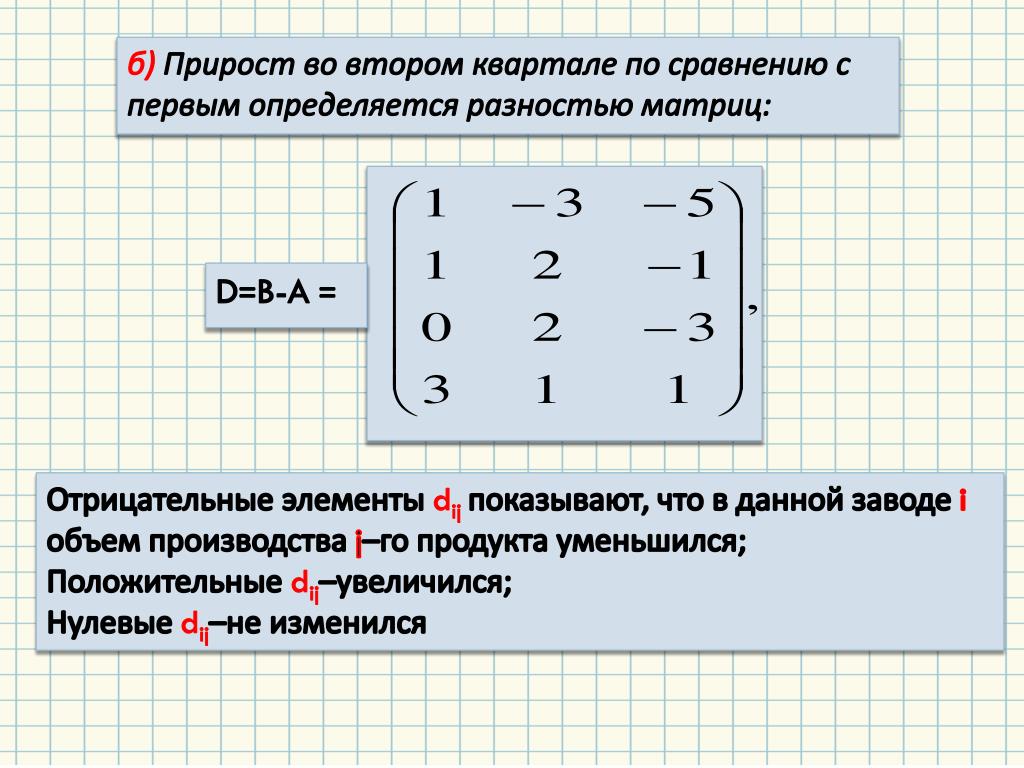  [15]

Страницы:      1

линейная алгебра — Каков геометрический смысл отрицательного определителя?

спросил

6 лет, 11 месяцев назад

Изменено 2 года, 7 месяцев назад

Просмотрено 29 тысяч раз

$\begingroup$

Геометрически определитель матрицы представляет собой объем единичного куба со знаком после применения преобразования, определяемого матрицей. Однако мне трудно понять, что здесь означает «подписанный». Поскольку на самом деле объемы только положительные (или нулевые, но пока не будем об этом беспокоиться). Итак, каков геометрический смысл отрицательного определителя? Как я должен понимать отрицательный объем, полученный при применении такого преобразования? 92$ с базисными элементами $(1,0)$ и $(0,1)$.

Мы можем считать, что $(1,0)$ указывает «вправо», а $(0,1)$ указывает «вперед».

Помещение $(1,0)$ и $(0,1)$ в матрицу дает единичную матрицу, определитель которой, конечно же, равен $1$.

Теперь поменяйте местами два базовых элемента. Представьте, что плоскость вращается вокруг линии $y=x$. Теперь $(1,0)$ указывает вперед, а $(0,1)$ указывает влево.

Конечно, если мы переставим строки в единичной матрице, результирующая матрица будет иметь определитель $-1$.

$\endgroup$

1

$\begingroup$

Я не понимаю, что здесь означает слово «подписано».

Под объемом со знаком понимают скалярное тройное произведение векторов ребер куба.

Итак, каков геометрический смысл отрицательного определителя?

Матрица имеет зеркальный компонент. Превращает левые руки в правые. Когда такая матрица преобразует треугольную сетку, она меняет порядок намотки треугольников.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

линейная алгебра — Что означает отрицательный определитель

спросил 2 года, 1 месяц назад

Изменено 7 месяцев назад

Просмотрено 2к раз

$\begingroup$

Я смотрел видео 3b1b по линейной алгебре. Я наткнулся на следующие моменты;

1. Отрицательный определитель означает, что ориентация пространства обратная. Если вы присваиваете своим пальцам измерения и если после преобразования эти присвоения остаются в силе, то это означает, что ориентация пространства не изменилась и определитель положителен.
2. Если после преобразования присваивание сохраняется на другой руке, то ориентация в пространстве меняется на противоположную, а это означает, что определитель отрицательный.

Мои сомнения

Q1. Может ли быть только два назначения, одно в левую руку, а другое в правую?
Q2. Если нет, то могут ли другие присваивания также означать перестановку пространственной ориентации и отрицательный определитель? То есть после преобразования, если присваивания не выполняются (ни слева, ни справа), значит ли это, что ориентация в пространстве обратная и определитель отрицательный? 92=1$, т.е. $\det R=\pm1$. Правые варианты осей связаны матрицами, удовлетворяющими $\det R=1$, как и левые, но для перехода от одного к другому используется матрица с $\det R=-1$. В частности, $\det R$ меняет знак всякий раз, когда мы меняем направление одной оси или меняем местами две оси.

$\endgroup$

$\begingroup$

Возможны только два назначения: правостороннее и левостороннее. Отрицательный определитель означает именно то, что он говорит.