N 1 факториал равен 1: 0! = 1? или почему факториал нуля равен единице / Хабр

Рекурсия | Ефремов А.А.

Мы уже сталкивались с тем, что функция может вызывать другую функцию. Но функция также может вызывать и саму себя! В этом случае она будет называться рекурсивной.

Рассмотрим в качестве примера функцию, которая вычисляет факториал числа n, то есть произведение чисел от 1 до n. Факториал числа n обозначается как n!, n! = 1 ⋅ 2 ⋅ … ⋅ n. Сначала напишем нерекурсивную реализацию этой функции:

def factorial(n):
     res = 1
     for i in range(2, n + 1):
          res *= i
     return res

Эта функция будет работать верно для всех неотрицательных значений n. При n, равном 0 или 1, цикл не выполнится ни разу, и функция, как и положено, будет возвращать число 1.

Теперь напишем

рекурсивную реализацию функции factorial().

Нам известно, что 0!=1, 1!=1. А как вычислить величину n! для большого n? Если бы мы могли вычислить величину (n — 1)!, то тогда легко вычислили бы n!, поскольку n! = n ⋅ (n — 1)! Но как вычислить (n — 1)!? Если бы мы вычислили (n — 2)!, то смогли бы вычислить (n — 1) != (n — 1) ⋅ (n — 2)! А как вычислить (n — 2)!? Если бы… В конце концов, мы дойдём до величины 0!, которая равна 1. Таким образом, для вычисления факториала мы можем использовать значение факториала для меньшего числа, а если n = 0, то сразу выводить ответ, равный 1:

def factorial(n):
     if n == 0:
          return 1
     else:
          return factorial(n — 1) * n

Давайте напишем рекурсивную функцию print_n(), которая печатает все числа от 1 до n для заданного числа n. Такая функция не будет ничего возвращать, а результатом её действий будут напечатанные ею числа. Сначала приведём нерекурсивную реализацию с использованием цикла for:

def print_n(n):
     for i in range(1, n + 1):
          print(i)

Теперь напишем рекурсивную реализацию. Для этого обратим внимание на то, что если n = 1, то нужно напечатать число 1. Если же n > 1, то нужно напечатать числа от 1 до n — 1 (а это умеет делать наша функция, если её вызвать с параметром n — 1), а затем напечатать число n. Получается, что при рекурсивном способе написания мы можем обойтись без цикла:

def print_n(n):
     if n == 1:
          print(1)
     else:
          print_n(n — 1)
          print(n)

Давайте попробуем в этой функции переставить две последние строки местами:

def print_n(n):
     if n == 1:
          print(1)
     else:
          print(n)
          print_n(n — 1)

Что будет делать такая функция? Так как сначала мы будем печатать число n, а потом вызывать функцию с параметром n — 1, то такая функция будет печатать числа от n до 1, то есть печатать то же самое, но в обратном порядке. Обратим внимание на то, что момент остановки рекурсии можно сделать другим. Мы переставали делать рекурсивные вызовы при условии n = 1. Но можно делать остановку рекурсии при n = 0. Тогда при n = 0 нам не нужно вообще ничего печатать. Тогда получим вот такую реализацию нашей функции:

def print_n(n):
     if n > 0:
          

print_n(n — 1)
          print(n)

Важно помнить, что при разработке рекурсивной функции необходимо прежде всего оформлять условие завершения рекурсии и думать, почему рекурсия когда-либо завершит работу. Если же у нас нет случая, при котором рекурсия прекращается, или этот случай не всегда достигается, то мы получим бесконечную рекурсию.

Задача 1

Не запуская код, ответьте на вопрос: что выведет на экран данная программа?

def f(x):
     if x > 0:
          g(x — 1)
def g(x):
     print(‘*’, end = ‘#’)
     if x > 1:
          f(x — 3)
f(11)

ОТВЕТ:
*#*#*#

Задача 2

Разворот последовательности

Дана последовательность натуральных чисел, заканчивающаяся числом 0. Выведите эту последовательность в обратном порядке.

При решении этой задачи нельзя пользоваться массивами и прочими динамическими структурами данных.

Входные данные

Вводится последовательность целых чисел, оканчивающаяся числом 0.

Выходные данные

Выведите ответ на задачу.

Примеры

Ввод	Вывод
1 2 3 0	0 3 2 1

ОТВЕТ:
def razvorot():
     x = int(input())
     if x != 0:
          razvorot()
     print(x)
razvorot()

Быстрое возведение в степень

Рассмотрим задачу о возведении числа в целую неотрицательную степень.

Напишем рекурсивную функцию, которая решает эту задачу:

def power(a, n):
     if n == 0:
          return 1
     else:
          return power(a, n — 1) * a

Такая функция будет работать очень долго, если степень n является большим числом. Например, для n = 100 такая функция сделает 100 вызовов самой себя. Чтобы вычислить степень числа быстрее, можно использовать следующее наблюдение. Для того чтобы вычислить a¹⁰⁰, можно сначала вычислить a⁵⁰, а затем возвести результат в квадрат. Аналогично, для вычисления a⁵⁰ нам потребуется a²⁵. Вычислить a²⁵ таким же способом не получится, так как число 25 — нечётное. Поэтому для вычисления a²⁵ используем значение a²⁴, как мы это делали в предыдущей реализации. В итоге получим вот такую рекурсивную функцию:

def power(a, n):
     if n == 0:
          return 1
     elif n % 2 == 1:
          return power(a, n — 1) * a
     else:
          a2 = power(a, n // 2)
          return a2 * a2

Можно заметить, что такая реализация будет работать значительно быстрее. Так, для n = 100 наша функция уже не 100 раз, а только 9 раз вызовет саму себя: a⁵⁰, a²⁵, a²⁴, a¹², a⁶, a³, a², a¹, a⁰.

Задача 3

Быстрое возведение в степень

Возводить в степень можно гораздо быстрее, чем за n умножений! Для этого нужно воспользоваться следующими рекуррентными соотношениями:

• aⁿ = (a²)^n/2 при чётном n,
• aⁿ = a ⋅ a^{n — 1} при нечётном n.

Реализуйте алгоритм быстрого возведения в степень. Если вы всё сделаете правильно, то количество умножений будет иметь порядок log₂n.

Нельзя использовать операцию возведения в степень.

Входные данные

Вводится действительное число a и целое неотрицательное число n.

Выходные данные

Выведите ответ на задачу.

Примеры

Ввод	Вывод
2 7	128

Ввод	Вывод
1. 00001 100000	2.71827

ОТВЕТ:
def f(a, n):

     def k(n):
          if n % 2 == 0:
               return True
          return False
     if n == 0:
          return 1
     if k(n):
          res = f(a, n / 2)
          return res * res
     return a * f(a, n — 1)
a = float(input())
n = int(input())
print(f(a, n))

Задача 4

Рекурсивный перевод

Напишите рекурсивную процедуру для перевода десятичного числа в P-‍ичную систему счисления.

В данной задаче запрещено использовать циклы и массивы.

Входные данные

На вход программе сначала подается значение P (1

Выходные данные

Вывод осуществляйте следующим образом: сначала выведите введённое число в десятичной системе счисления, за ним укажите его систему счисления в круглых скобках, то есть (10), затем поставьте знак «=», после чего выведете результат работы вашей программы — число в P-‍ичной системе счисления, за ним укажите его систему счисления в круглых скобках.

Весь вывод осуществляется без пробелов.

Примеры

Ввод	Вывод
3 123	123(10)=11120(3)

ОТВЕТ:
p, d = 0, 0
p = int(input())
d = int(input())
def pSys(d, p):
     if p > d:
          return str(d)
     return pSys(d // p, p) + str(d % p)
print(str(d) + ‘(10)=’ + pSys(d, p) + ‘(‘ + str(p) + ‘)’)

Задача *

Количество разбиений на слагаемые

Дано натуральное число N. Найдите количество его разбиений на натуральные слагаемые. Два разбиения, отличающиеся только порядком слагаемых, будем считать за одно.

Например, для N = 5 существует 7 различных разбиений:

5 = 5
5 = 4 + 1
5 = 3 + 2
5 = 3 + 1 + 1
5 = 2 + 2 + 1
5 = 2 + 1 + 1 + 1
5 = 1 + 1 + 1 + 1 + 1

Входные данные

Задано единственное число N ⩽ 30.

Выходные данные

Выведите количество различных разбиений на слагаемые.

Примеры

Ввод	Вывод
5	7

Видеоразбор

ОТВЕТ:
def num(n, k):
     if n == 0:
          return 1
     ans = 0
     for d in range(1, min(n, k) + 1):
          ans += num(n — d, d)
     return ans
n = int(input())
print(num(n, n))

Задача 5

Лесенки

Лесенкой называется набор кубиков, в котором каждый следующий горизонтальный слой содержит меньше кубиков, чем слой под ним.

Требуется подсчитать количество различных лесенок, которые могут быть построены ровно из N кубиков.

Входные данные

Вводится одно число N(1 ⩽ N ⩽ 50).

Выходные данные

Выведите искомое количество лесенок.

Примеры

Ввод	Вывод
3	2

ОТВЕТ:
def stairway(k, n):
     ans = 0
     if n == 0:
          return 1
     elif k           for i in range(k + 1, n + 1):
               ans += stairway(i, n — i)
          return ans
     else:
          return ans
n = int(input())
print(stairway(0, n))

Рекурсия. Подключение стандартных модулей

В языке Python имеется ограничение на максимальную глубину рекурсии. Допустим, мы вызвали функцию для вычисления факториала числа n. Эта функция вызовет себя с параметром n — 1, а внутри этого вызова будет вызвана функция с параметром n — 2, и так пока значение параметра не дойдёт до значения 0. Таким образом, возникнет цепочка рекурсивных вызовов, которая уходит на глубину n. Если, например, n = 1000, то мы получим ошибку исполнения, связанную с превышением максимально допустимой глубины рекурсии.

Внутри языка Python есть счётчик, который хранит глубину рекурсии. Если значение глубины рекурсии превышает максимально допустимое значение, то программа получает ошибку во время исполнения. Это сделано для того, чтобы избежать ошибок, связанных с условием завершения рекурсии, которые приводят к бесконечной рекурсии и переполнению памяти компьютера. Бывают ситуации, когда ограничение на максимальную допустимую глубину рекурсии требуется увеличить. Например, если мы хотим вычислить факториал числа больше 1000 с использованием рекурсивной функции. Для этого есть специальная функция в языке Python, которая называется setrecursionlimit(). Для того чтобы её использовать, требуется подключить модуль sys, в котором она лежит. Чтобы увеличить максимально допустимую глубину рекурсии до миллиарда, надо написать:

import sys
sys.setrecursionlimit(10 ** 9)

В этом примере мы подключили модуль sys и после этого использовали функцию setrecursionlimit() из этого модуля, при этом мы должны указывать перед именем функции название модуля и разделять эти имена точкой: sys.setrecursionlimit().

Однако, даже после этого мы можем получить ошибку выполнения программы. Дело в том, что у операционной системы есть своё ограничение на размер стека, которое может зависеть от различных факторов, и мы его превысили. Но нескольких миллионов глубина рекурсии достигать может.

В языке Python имеется много полезных модулей, которые можно подключить и использовать функции, которые в них имеются. Например, можно подключить модуль random для работы со случайными числами:

import random

Можно подключить модуль math, в котором лежат различные математические функции:

import math

В модуле math есть такие функции, как sqrt() для вычисления квадратного корня, factorial() для вычисления факториала числа, тригонометрические функции, экспонента, логарифм и многие другие.

Для копирования вложенных списков или других сложных объектов может понадобиться модуль copy:

import copy

Если мы подключили модуль math и хотим использовать функцию квадратного корня из этого модуля, то мы должны не забыть через точку указать название модуля перед названием функции:

math.sqrt(2)

С одной стороны, это удобно. Потому что мы можем написать свою функцию sqrt(), и это не приведёт к ошибке, так как функции sqrt() и math.sqrt записываются различным образом.

С другой стороны, не всегда хочется писать название модуля каждый раз перед вызовом функции. Чтобы этого не делать, можно использовать другой способ импортировать функции из модуля:

from math import sqrt
sqrt(2)

Можно импортировать сразу несколько функций из модуля:

from math import sqrt, factorial
print(sqrt(2), factorial(5))

Также можно импортировать сразу все функции из модуля следующей строчкой:

from math import *

Задача 6

Функция Аккермана

Требуется вычислить значение A(m,n) — где A это функция Аккермана.

Функция Аккермана определяется рекурсивно для неотрицательных целых чисел m и n следующим образом:

• A(m, n) = n + 1, при m = 0
• A(m, n) = A(m — 1, 1), при m > 0, n = 0
• A(m, n) = A(m — 1, A(m, n — 1)), при m > 0, n > 0

Входные данные

Даны два целых числа m и n (0 ⩽ m ⩽ 3, 0 ⩽ n ⩽ 7).

Выходные данные

Выведите одно число — A(m, n).

Примеры

Ввод	Вывод
1 1	3

Ограничения

Время выполнения: 2 секунды

ОТВЕТ:
import sys
sys.setrecursionlimit(10 ** 9)
m, n = 0, 0
s = {}
def a(m, n):
     if not(m, n) in s:
          if m == 0:
               ans = n + 1
          if m > 0 and n == 0:
               ans = a(m — 1, 1)
          if m > 0 and n > 0:
               ans = a(m — 1, a(m, n — 1))
          s[(m, n)] = ans
     return s[(m, n)]
m, n = map(int, input(). split())
print(a(m, n))

Задача *

Ханойские башни

Головоломка «Ханойские башни» состоит из трёх стержней, пронумерованных числами 1, 2, 3. На стержень 1 надета пирамидка из n дисков различного диаметра в порядке возрастания диаметра дисков, если рассматривать их сверху вниз. Диски можно перекладывать с одного стержня на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку со стержня 1 на стержень 3, используя стержень 2 как вспомогательный, за минимальное число перекладываний.

Напишите функцию, которая решает головоломку: для данного числа дисков n печатает последовательность перекладываний в формате a b c, где a — номер перекладываемого диска, b — номер стержня, с которого снимается данный диск, c — номер стержня, на который надевается данный диск.

Например, строка 1 2 3 означает перемещение диска номер 1 со стержня 2 на стержень 3. В одной строке печатается одна команда.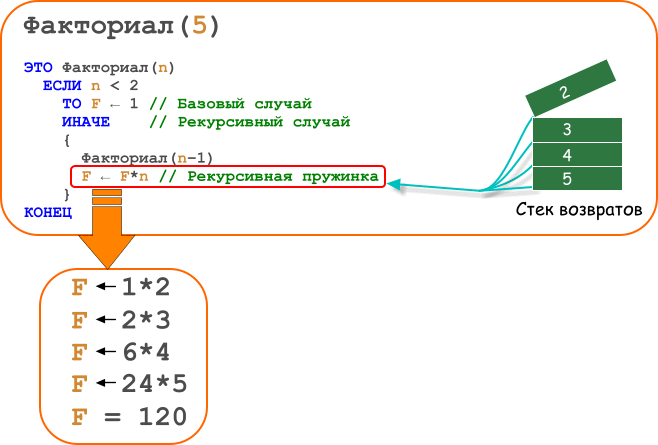 Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.

Входные данные

Задано натуральное число n ⩽ 10 — размер пирамидки.

Выходные данные

Программа должна вывести минимальный (по количеству произведённых операций) способ перекладывания пирамидки из данного числа дисков.

Примеры

Ввод	Вывод
3	1 1 3 2 1 2 1 3 2 3 1 3 1 2 1 2 2 3 1 1 3

Видеоразбор

ОТВЕТ:
n = 0
def move(n, start, finish):
     if n > 0:
          tmp = 6 — start — finish
          move(n — 1, start, tmp)
          print(n, start, finish)
          move(n — 1, tmp, finish)
n = int(input())
move(n, 1, 3)

Задача *

Циклические башни

На дорогах Ханоя было введено одностороннее круговое движение, поэтому теперь диск со стержня 1 можно перекладывать только на стержень 2, со стержня 2 — на 3, а со стержня 3 — на 1.

Решите головоломку с учётом этих ограничений. Вам не нужно находить минимальное решение, но количество совершённых перемещений не должно быть больше 200000 при условии, что количество дисков не превосходит 10.

Входные данные

Задано натуральное число n ⩽ 10 — размер пирамидки.

Выходные данные

Программа должна вывести способ перекладывания пирамидки из данного числа дисков со стержня 1 на стержень 3.

Примеры

Ввод	Вывод
3	1 1 2 1 2 3 2 1 2 1 3 1 2 2 3 1 1 2 1 2 3 3 1 2 1 3 1 1 1 2 2 3 1 1 2 3 1 3 1 3 2 3 1 1 2 1 2 3 2 1 2 1 3 1 2 2 3 1 1 2 1 2 3

Видеоразбор

ОТВЕТ:
def move(n, start, finish):
     if n > 0:
          tmp = 6 — start — finish
          if (finish — start) % 3 == 1:
               move(n — 1, start, tmp)
               print(n, start, finish)
               move(n — 1, tmp, finish)
          else:
               move(n — 1, start, finish)
               print(n, start, tmp)
               move(n — 1, finish, start)
               print(n, tmp, finish)
               move(n — 1, start, finish)
move(int(input()), 1, 3)

Задача 7

Фишки

Дана полоска из клеток, пронумерованных от 1 до N слева направо. Разрешено:

• Снимать или ставить фишку на клетку с номером 1.
• Ставить фишку на клетку, следующую за самой левой из установленных фишек (правее неё), если она пуста.
• Удалять фишку на клетке, следующей за самой левой из установленных фишек (правее неё), если она занята.

Изначально полоска пуста. Нужно разместить фишки во всех клетках.

Входные данные

Программа получает на вход количество клеток в полоске N(1 ⩽ N ⩽ 10).

Выходные данные

Программа должна вывести последовательность номеров клеток, с которыми совершается действие. Если фишка снимается, то номер клетки должен выводиться со знаком минус. Количество действий не должно превышать 10⁴. Если существует несколько возможных решений задачи, то разрешается вывести любое.

Примеры

Ввод	Вывод
3	1 2 -1 3 1

ОТВЕТ:
n = 0
def a(n):
     if n           return list(range(-n, 0))
     return a(n — 2) + [-n] + b(n — 2) + a(n — 1)
def b(n):
     if n           return list(range(1, n + 1))
     return b(n — 1) + a(n — 2) + [n] + b(n — 2)
print(*b(int(input())))

 

Рекурсия.

Декораторы. Генераторы — Основы Python

Рассмотрим задачу получения факториала числа. В математике он обозначается «!» и функция факториала описывается так:

1. 0! = 1.
2. n! = 1 * 2 * … * n, n > 0.

Напишем функцию, вычисляющую факториал числа n.

def fact(n):
    factorial = 1
    for i in range(2, n + 1):
        factorial *= i
    return factorial
print(fact(5))

Давайте немного перепишем определение факториала:

1. 0! = 1.
2. n! = (1 * 2 * … * (n — 1)) *n = (n — 1)! * n

Мы видим, что для вычисления n! нам нужно найти (n - 1)! и умножить результат на n. Таким образом, мы используем функцию для вычисления нового значения функции. Функции, в которых происходит вызов самих этих функций называют рекурсивными.

Давайте напишем рекурсивную функцию для вычисления факториала. При создании рекурсивных функций необходимо:

1. Написать, что вернёт функция при начальном значении аргумента.
2. Написать правило получения нового значения на основе уже вычисленных на предыдущих шагах.

def fact(n):
    if n == 0:  # 0! = 1
        return 1
    return fact(n - 1) * n  # n! = (n - 1)! * n
print(fact(5))

Вывод программы:

120

Обратите внимание, что рекурсивный вариант функции выполняет действия, которые описаны правилом вычисления факториала. Такой стиль программирования называется декларативным. Данный подход описывает сам результат. Функции, которые мы писали ранее, основаны на императивном стиле, и отвечают на вопрос о способе получения результата.

Рассмотрим применение рекурсивной функции для вычисления n-го числа последовательности Фибоначчи. Числа Фибоначчи — последовательность чисел, вычисляемых по следующему правилу:

1. Первые два числа последовательности равны 1.
2. n-ое число Фибоначчи равно сумме двух предыдущих, то есть fib(n) = fib(n — 1) + fib(n — 2).

Программа с рекурсивной функцией вычисления n-го числа Фибоначчи запишется так:

def fib(n):
    if n in (0, 1):
        return 1
    return fib(n - 1) + fib(n - 2)
print(fib(35))

Вывод программы:

14930352

При запуске программы, можно заметить, что вычисление 35-го числа последовательности происходит с небольшой задержкой. Проверим, сколько времени занимают вычисления. Выполним вычисления 10 раз и выведем среднее время вычисления с точностью 1 мс. В тестировании скорости работы кода нам помогает стандартный модуль timeit.

from timeit import timeit
def fib(n):
    if n in (0, 1):
        return 1
    return fib(n - 1) + fib(n - 2)
print(f"Среднее время вычисления: "
      f"{round(timeit('fib(35)', number=10, globals=globals()) / 10, 3)} с.")

Вывод программы:

Среднее время вычисления: 2.924 с.

Проверим, сколько времени займут те же вычисления у императивной версии функции.

from timeit import timeit
def fib(n):
    f_1, f = 1, 1
    for i in range(n - 1):
        f_1, f = f, f_1 + f
    return f
print(f"Среднее время вычисления: "
      f"{round(timeit('fib(35)', number=10, globals=globals()) / 10, 3)} с.")

Вывод программы:

Среднее время вычисления: 2e-06 с.

Получили результат 2 микросекунды у императивной функции против почти 3 секунд у рекурсивной. В чём же причина?

Проблема рекурсивной функции заключается в том, что внутри неё происходит два вызова самой себя для каждого значения. И так до тех пор, пока не функция не дойдет до начальных значений аргументов (1 и 1). В итоге появляется несколько рекурсивных веток, которые образуют рекурсивное дерево. Покажем его часть на рисунке.

Числа на схеме показывают номер числа Фибоначчи. Цветом показаны числа с одинаковым номером. Из схемы дерева становится понятно, что рекурсивная реализация функции выполняет много одинаковых вычислений. Давайте добавим счётчик количества вызовов нашей рекурсивной функции:

def fib(n):
    global count
    count += 1
    if n in (0, 1):
        return 1
    return fib(n - 1) + fib(n - 2)
count = 0
print(f"35-ое число Фибоначчи равно: {fib(35)}.")
print(f"Количество вызовов рекурсивной функции равно: {count}.")

Вывод программы:

35-ое число Фибоначчи равно: 14930352.
Количество вызовов рекурсивной функции равно: 29860703. 

Для ускорения вычислений нужно запоминать уже посчитанные числа последовательности, а затем использовать их при необходимости. Такой подход называют кэшированием или мемоизацией.

Напишем рекурсивную функцию с кэшированием, использовав для сохранения вычисленных значений словарь, в котором ключами будут номера чисел последовательности, а значения — сами числа.

def fib(n):
    global count
    count += 1
    if n not in cash:
        cash[n] = fib(n - 1) + fib(n - 2)
    return cash[n]
count = 0
cash = {0: 1, 1: 1}
print(f"35-ое число Фибоначчи равно: {fib(35)}.")
print(f"Количество вызовов рекурсивной функции равно: {count}.")

Вывод программы:

35-ое число Фибоначчи равно: 14930352.
Количество вызовов рекурсивной функции равно: 69.

За счет кэширования количество вызовов рекурсивной функции существенно сократилось. Проверим скорость работы нашей функции.

from timeit import timeit
def fib(n):
    global count
    count += 1
    if n not in cash:
        cash[n] = fib(n - 1) + fib(n - 2)
    return cash[n]
count = 0
cash = {0: 1, 1: 1}
print(f"Среднее время вычисления: "
      f"{round(timeit('fib(35)', number=10, globals=globals()) / 10, 6)} с. ")

Вывод программы:

Среднее время вычисления: 2e-06 с.

Скорость работы также существенно увеличилась. Попробуем вычислить число Фибоначчи с номером 1000:

from timeit import timeit
def fib(n):
    if n not in cash:
        cash[n] = fib(n - 1) + fib(n - 2)
    return cash[n]
cash = {0: 1, 1: 1}
print(f"Среднее время вычисления: "
      f"{round(timeit('fib(1000)', number=10, globals=globals()) / 10, 6)} с.")

Вывод программы:

RecursionError: maximum recursion depth exceeded

Программа выдала ошибку по превышению глубины рекурсии. В Python по умолчанию максимальный размер глубины рекурсии равен 1000. Для изменения глубины рекурсии для вашей программы нужно вызвать функцию setrecursionlimit() из стандартного модуля sys и передать новое значение для предела глубины.

from timeit import timeit
from sys import setrecursionlimit
def fib(n):
    if n not in cash:
        cash[n] = fib(n - 1) + fib(n - 2)
    return cash[n]
setrecursionlimit(2000)
cash = {0: 1, 1: 1}
print(f"Среднее время вычисления: "
      f"{round(timeit('fib(1000)', number=10, globals=globals()) / 10, 6)} с. ")

Вывод программы:

Среднее время вычисления: 0.000132 с.

Обратите внимание: максимально возможное значение глубины рекурсии зависит от операционной системы. Поэтому бесконечно его увеличивать не получится.

Итак, наша рекурсивная функция с кэшированием стала работать быстро. Однако есть и недостаток: её код стал читаться сложнее. Поручим процесс запоминания промежуточных значений функции интерпретатору. Для этого в Python в стандартном модуле functools есть функция lru_cache. Её следует использовать так, как показано в следующем примере:

from timeit import timeit
from functools import lru_cache
@lru_cache(maxsize=1000)
def fib(n):
    if n in (0, 1):
        return 1
    return fib(n - 1) + fib(n - 2)
    
print(f"Среднее время вычисления: "
      f"{round(timeit('fib(35)', number=10, globals=globals()) / 10, 6)} с.")

Вывод программы:

Среднее время вычисления: 2e-06 с.

Благодаря автоматическому кэшированию, наша функция снова приобрела «декларативный» вид и при этом работает быстро.

Функция lru_cache в примере используется как декоратор. Подробнее о них можно почитать в этом материале

Как может $0!=1$, если определение факториала $n!=n\times (n-1)!$

спросил 7 лет, 9 месяцев назад

Изменено 7 лет, 9 месяцев назад

Просмотрено 507 раз

$\begingroup$

Довольно простой вопрос.

Если определение факториала $n!= n\times(n-1)!$, то как может $0!=1$, поскольку если мы подставим $0$ в уравнение, мы получим $0!=0\times (-1)!$?

Это происходит после видео Numberphile, в котором они объясняют, что вы можете написать $4!=\frac{5!}5$, тогда вы можете сказать, что $0!=\frac{1!}1$, что равняется $1$.

Еще говорят, что есть один способ ничего не устраивать, но я бы сказал, что есть $0$ способов ничего не устраивать, так как нечего устраивать.

• факториал

$\endgroup$

3

$\begingroup$

Хорошее определение $n!$ — это количество биекций из $\{1,2,\dots,n\}$ в себя. Таким образом, $0!$ — это количество биекций из пустого множества в себя. Есть одна такая карта, которую можно рассматривать как своего рода пустой продукт.

$\endgroup$

2

$\begingroup$

Насчет того, почему существует один способ расставить нулевые объекты, я однажды прочитал очень хорошее объяснение: чтобы подсчитать количество способов упорядочить что-либо, вы фотографируете все возможные варианты расположения предметов, а затем подсчитываете количество отчетливых картинок. Для нулевых элементов в аранжировках не будет элементов, но у вас все равно будет одна единственная картина ничего, представляющая единую аранжировку. 90 = 1 $$

$\endgroup$

$\begingroup$

Примечание: Я сочувствую вашему вопросу, потому что раньше он меня тоже беспокоил. Казалось абсурдным, что некоторые авторы учебников могли обойтись, допуская $0!=1$, потому что это было «удобно определить, чтобы это было так» (не могу точно вспомнить, из какой книги это произошло). Во-первых, обратите внимание, что заголовок вашего вопроса не имеет большого смысла в контексте определений, потому что $0!$ на самом деле 9н к $$ и $$ п!= \begin{случаи} 1 & \text{если $n=0$},\\ (n-1)!\cdot n & \text{если $n>0$}. \end{случаи} $$ Таким образом, вы действительно не можете доказать , что $0!=1$. Это не имеет никакого смысла. Тем не менее, может быть некоторая интуиция, которую можно получить с помощью комбинаторики.

Немного интуиции через комбинаторику: Возможно, вы когда-то встречали обозначение $\binom{n}{r}=\frac{n!}{r!(n-r)!}$. Когда $r\leq n$, запись $\binom{n}{r}$ представляет количество способов выбрать объекты $r$ из объектов $n$ независимо от их порядка. Теперь предположим, что $r=n$. Что это значит? Это означает, что вы выбираете все объекты одновременно, и есть несколько способов сделать это. $$\требовать{отмена} \binom{n}{r} = \frac{n!}{n!(n-n)!} = \frac{\cancel{n!}}{\cancel{n!}\cdot 0!} = \frac{ 1}{0!} = 1. $$ Следовательно, $0!=1$.

Это , а не доказательство — просто некоторая возможная интуиция.

$\endgroup$

5

$\begingroup$

Уравнение $n! = n \cdot (n-1)!$ выполняется только для $n \geq 1$, поэтому вам не разрешено вставлять $n=0$, как в вопросе.

Попробуйте вместо этого вставить $n=1$. Получаем:

$$1! = 1 \cdot 0!$$

Отсюда

$$1! = 0!$$

Итак, если вы согласны с тем, что $1!$ равно $1$, тогда:

$$1 = 0!$$

$\endgroup$

$\begingroup$

Мы просто определяем 0! быть равным 1. Кроме того, это определение хорошо сочетается с гамма-функцией.

$\endgroup$

4

$\begingroup$

Если мы подставим $0$ в уравнение, мы получим $0!=0\раз(-1)!$

А? В чем проблема? $(-1)!~$ равно $~\pm\infty,~$ или, выражаясь более строго, равно

undefined. Более того, $~\displaystyle\lim_{x\to0}x\cdot(x-1)!~=~\lim_{x\to0}x\cdot\Gamma(x)~=~1$.

$\endgroup$

0

$\begingroup$

Потому что мы сначала получаем 0 на 1! = 1*0!, и это дает 0! = 1.

Когда мы пытаемся добраться до -1!, мы получили 0! = 0*(-1)! что, по наивности, Говорит, что $(-1)! = \infty$.

Фактически это означает, что (-н)! не определено для целого числа n < 0.