Графический метод решения системы уравнений с двумя переменными
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Математика уступает
Свои крепости лишь
Сильным и смелым
А.П. Конфорович
‘Графический метод решения
системы уравнений с двумя
переменными’
2. Цель урока: Научить решать систему уравнений с двумя переменными графическим методом. Рассмотреть частные случаи решения
системы линейных уравнений.
3. Что называют системой уравнений? Рассмотрим два линейных уравнения: 1) y – 2x = – 3 2) x + y = 3
Системой уравнений называется некотороеколичество уравнений, объединенных фигурной
скобкой. Фигурная скобка означает, что все
уравнения должны выполняться одновременно.
a1 x b1 y c1 ,
a2 x b2 y c2 .
y – 2x = – 3
x+y=3
Каждая пара значений переменных, которая
одновременно является решением всех
уравнений системы, называется решением
системы.
Решением системы уравнений с двумя
переменными называется пара значений
переменных, обращающая каждое уравнение
системы в верное равенство.
Решить систему уравнений — значит найти все её
решения или установить, что их нет.
Решение системы графическим способом
у – х = 2,
у + х = 10;
Выразим у
через х
y
y=x+2
10
у = х + 2,
у = 10 – х;
Построим график первого уравнения
6
у=х+2
х 0 -2
у 2 0
y=10 — x
2
1
Построим график второго уравнения
у = 10 – х
х 0 10
у 10 0
-2
0
1
Ответ: (4; 6)
4
10
x
6.
Алгоритм решения системы уравнений графическим способом1. Приводим оба уравнения к виду линейной функцииy = k x + m.
2. Составляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной плоскости.
4. Определяем число решений:
Если прямые пересекаются, то одно решение пара чисел (х ; у) –
координаты точки пересечения;
Если прямые параллельны, то нет решений;
Если прямые совпадают, то бесконечно много решений.
5. Записываем ответ.
7. Графический метод решения системы x + y = 3 y – 2x = – 3
Графический метод решения системыу =3–x
x
y
0
3
3
0
A(0;3)
M(2;1)
у =1
у = 2x – 3
D(3;3)
B(3;0)
X=2
x
y
0
3
–3
3
C(0; – 3)
Ответ: (2; 1)
x+y=3
y – 2x = – 3
Решим
систему
уравнений:
Y= 0,5x+2
Y= 0,5x-1
Y=0,5x+2
x y
0
2
2
3
B(2;3)
A(0;2)
D(2;0)
Y=0,5x-1
x y
0 -1
2 0
C(0;-1)
Графики функций
параллельны и не
пересекаются.
Ответ: Система не имеет решений.
Y=x+3
x
y
0
3
-3
0
D(1;4)
Система
Y=x+3
A(0;3)
Y=x+3
C(-1;2)
B(-3;0)
Y=x+3
x y
1
4
-1
2
Графики функций
совпадают.
Ответ: система имеет бесконечное множество решений
Если графиками уравнений, входящих в систему линейных уравнений,
являются прямые, то количество решений этой системы зависит от
взаимного расположения двух прямых на плоскости:
Прямые
Общие точки
Система
имеет
О системе говорят
Пересекаются
Одна общая точка Одно решение
Имеет решение
Параллельны
Нет общих точек
Не имеет
решений
Несовместна
Совпадают
Много общих
точек
Много решений Неопределена
Частные случаи пересечения графиков линейных
функций (памятка)
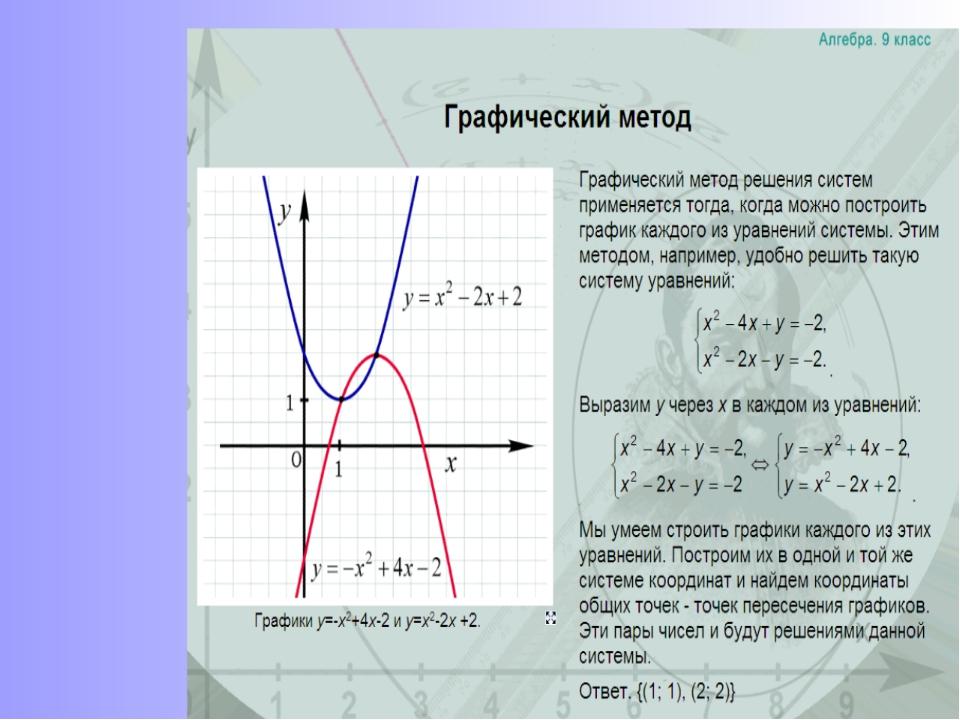
2) Решите систему уравнений:
х у 1,
2 х у 4.
у
1) х – у = -1,
у=х+1
х у
0 1
2 3
2) 2х + у = 4,
у = 4 — 2х
х у
0 4
2 0
Ответ: х = 1, у = 2.
4
3
2
1
1
1
2
3
х
1) Решите систему уравнений:
1) 3х +2у = 7,
2у = 7 — 3х,
у = (7 — 3х):2,
у = 3,5 -1,5х,
у = -1,5х + 3,5.
у х
1 2
3 -1
Ответ: х = 3, у = -1.
3х 2 у 7,
2 х 4 у 2.
2) 2х + 4у = 2,
4у = 2 — 2х,
у = (2 — 2х):4,
у = 0,5 – 0,5х.
х
1
3
у
0
-1
у
4
3
2
1
1
1
2
3
х
14. Решите систему уравнений графическим способом
1 варианту = 2х — 3
у=-х+3
2 вариант
у = 3х — 4
у = 0,5х + 1
Проверь себя!
Правильное решение систем уравнений графическим способом:
.
у
.
.
. А(2;1)
.
у
х
Ответ: А ( 2; 1)
.
.
.
.
.В(2;2)
х
Ответ: В ( 2; 2)
16. Домашнее задание:
§ 26, выучить материал со слайдов3, 4, 6,10 (переписать в рабочую
тетрадь)
№ 1008, 1010(1)
English Русский Правила
урок «Графический метод решения системы уравнений с двумя переменными» | Презентация урока для интерактивной доски по алгебре (7 класс) по теме:
Слайд 1
«Графический метод решения системы уравнений с двумя переменными« 7 класс Абраменкова Валентина Борисовна МОУ «СОШ № 21 с УИОП» г.
Ухта, Республика Коми 2014 год
Слайд 2
Цель урока: Научить решать систему уравнений с двумя переменными графическим методом. Рассмотреть частные случаи решения системы линейных уравнений.
Слайд 3
1. у = 5 х – 3 2 . у = – 0,2 х + 7 3. у = х + 1,3 Назовите угловые коэффициенты линейных функций. Что является графиком линейной функции? Какие прямые образуют с осью Х острый угол? Тупой угол? От чего это зависит? Назовите координаты точки пересечения первой прямой с осью У . Найдите значение второй функции в точке с абсциссой 5.
Слайд 4
Что называют системой уравнений ? Рассмотрим два линейных уравнения: 1) y – 2 x = – 3 2) x + y = 3 Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно. y – 2 x = – 3 x + y = 3
Слайд 5
Решить систему уравнений — значит найти все её решения или установить, что их нет. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы.
Слайд 6
Способы решения линейных уравнений
Слайд 7
Алгоритм решения системы уравнений графическим способом 1 . Приводим оба уравнения к виду линейной функции y = k x + m . 2. Составляем расчётные таблицы для каждой функции. 3. Строим графики функций в одной координатной плоскости. 4. Определяем число решений: Если прямые пересекаются, то одно решение пара чисел ( х ; у) – координаты точки пересечения; Если прямые параллельны, то нет решений; Если прямые совпадают, то бесконечно много решений. 5. Записываем ответ.
Слайд 8
1 0 1 2 10 x 4 6 10 -2 y y=10 — x y=x+2 у – х = 2, у + х = 10; у = х + 2, у = 10 – х ; Построим график первого уравнения х у 0 2 -2 0 у = х + 2 Построим график второго уравнения у = 10 – х х у 0 10 10 0 Ответ: (4; 6) Решение системы графическим способом Выразим у через х
Слайд 9
у = 3 – x у = 2x – 3 x y 0 3 x y 0 3 3 0 – 3 3 A(0;3) B(3;0) C(0; – 3) D(3;3) M(2;1) X=2 у =1 Ответ: (2; 1) Графический метод решения системы x + y = 3 y – 2 x = – 3
Слайд 10
Y=0,5x-1 Y=0,5x+2 x x y y 0 2 2 3 0 -1 2 0 A(0;2) B(2;3) C(0;-1) D(2;0) Решим систему уравнений : Y= 0 ,5 x+2 Y= 0,5x-1 Графики функций параллельны и не пересекаются.
Ответ: Система не имеет решений.
Слайд 11
Y=x+3 Y=x + 3 x y 0 — 3 x y 1 -1 3 0 4 2 A(0;3) B( — 3;0) C( -1 ; 2 ) D( 1 ; 4 ) Система Y=x+3 Y=x+3 Графики функций совпадают. Ответ: система имеет бесконечное множество решений
Слайд 12
Прямые Общие точки Система имеет О системе говорят Одна общая точка Одно решение Имеет решение Нет общих точек Не имеет решений несовместна Много общих точек Много решений неопределена
Слайд 13
Частные случаи пересечения графиков линейных функций (памятка)
Слайд 14
Решите систему уравнений графическим способом (памятка) Х 0 2 У у = 3 х + 4 у = 3 х — 2 х 0 -2 у у = 3 х — 2 у = 3 х + 4
Слайд 15
1 вариант Решите систему уравнений графическим способом у = 2 х — 3 у = — х + 3 2 вариант у = 0,5 х + 1 у = 3 х — 4
Слайд 16
вывод: 1) угловые коэффициенты не равны , 2) прямые пересекаются. у х х у . . . . А(2;1) . . . . . . В(2;2) У = 2х — 3 У = — х + 3 У = 0,5 х + 1 У = 3 х — 4 Ответ: А ( 2; 1) Ответ: В ( 2; 2)
Слайд 17
Найдём координаты точек пересечения графиков 2х – 3 = — х + 3, 2х + х = 3 + 3, 3х = 6, х = 2, у = 2 • 2 — 3, у = 1.
Ответ: А ( 2; 1). 3х – 4 = 0,5х + 1, 3х – 0,5х = 1 + 4, 2,5х = 5, х = 2, у = 3 • 2 – 4, у = 2. Ответ: В ( 2; 2).
Слайд 18
Решите систему уравнений графическим способом Х 0 2 У у = 3 х + 4 у = 3 х — 2 х 0 -2 у у = 3 х — 2 у = 3 х + 4
Слайд 19
Домашнее задание: 1. Решите с помощью графиков систему уравнений: 2 . Подберите если возможно, такое значение к , при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений: а) б) в)
Слайд 20
3 4 1 2 Научился ли я решать систему графическим методом; понял ли я алгоритм решения систем линейных уравнений графическим методом; смогу ли я использовать при решении частные случаи; могу ли я по виду системы узнать о количестве решений системы.
Слайд 21
Спасибо за урок
Решение квадратных уравнений с помощью графиков
Давайте изучим, как решать квадратные уравнения, глядя на их графики.
Стандарты TEKS и ожидания учащихся
A(1) Стандарты математических процессов. Студент использует математические процессы, чтобы приобрести и продемонстрировать математическое понимание. Студент должен:
A(1)(C) выбор инструментов, включая реальные объекты, манипуляции, бумагу и карандаш, а также соответствующие технологии, а также приемы, включая ментальную арифметику, оценку и чувство чисел, для решения задач
A(1)(D) сообщать математические идеи, рассуждения и их последствия, используя различные представления, включая символы, диаграммы, графики и соответствующий язык
A(8) Квадратичные функции и уравнения. Учащийся применяет стандарты математического процесса для решения квадратных уравнений с помощью технологий и без них и оценивает обоснованность их решений. Студент формулирует статистические зависимости и оценивает их обоснованность на основе реальных данных.
Студент должен:
A(8)(A) решать квадратные уравнения, имеющие действительные решения, путем разложения на множители, извлечения квадратных корней, завершения квадрата и применения квадратной формулы
Цель(и) ресурсов учащийся будет использовать графические методы для решения уравнения.
Основные вопросы
Как решить квадратное уравнение, глядя на график?
Как узнать, сколько решений имеет квадратное уравнение?
- Коэффициент
- y -Перехват
- Квадратное уравнение
- Функция
- x -Перехват
- Нули
- Корень
- Константа
Давайте рассмотрим способы использования графика для представления и определения решения квадратного уравнения.
График и таблица ниже показывают точки для квадратичной функции y = х ² − х − 6.
Как график, так и таблицу значений можно использовать для решения уравнения x ² − x – 6 = 0, которое связано с функцией y = x ² – x − 6.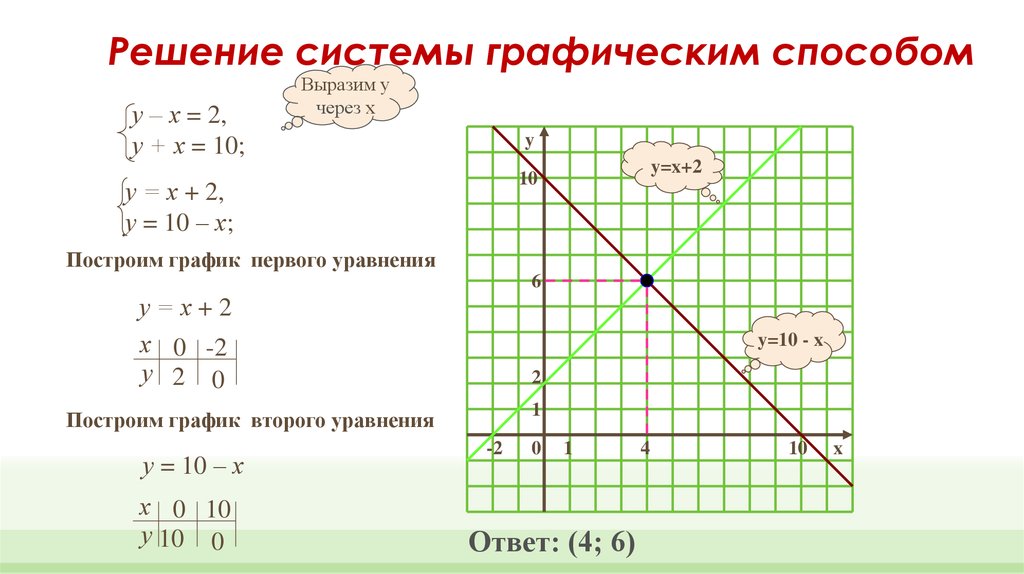
Вы можете найти, когда y = 0 в таблице, и значение x в этой точке решит функцию. Значение x , где график пересекает ось x , также можно использовать для решения квадратного уравнения. Вы будете использовать аналогичный подход для поиска точек на графиках, удовлетворяющих определенным условиям.
Хотя все квадратичные функции имеют решение, оно не всегда может быть действительным числом. Следовательно, квадратичная функция может иметь два действительных корня, один действительный корень или ноль действительных корней.
Изучите три графика ниже. Нажмите на знак «плюс» у кнопки «Пуск», чтобы узнать больше об их решениях.
График — это изображение точек, которые делают функцию истинной. Например, на графике и в таблице ниже показаны точки для квадратичной функции y = x 9.0054 ² – х – 6.
Как график, так и таблица значений могут быть использованы для решения уравнения Нажимайте на каждый вопрос, чтобы проверить свой ответ.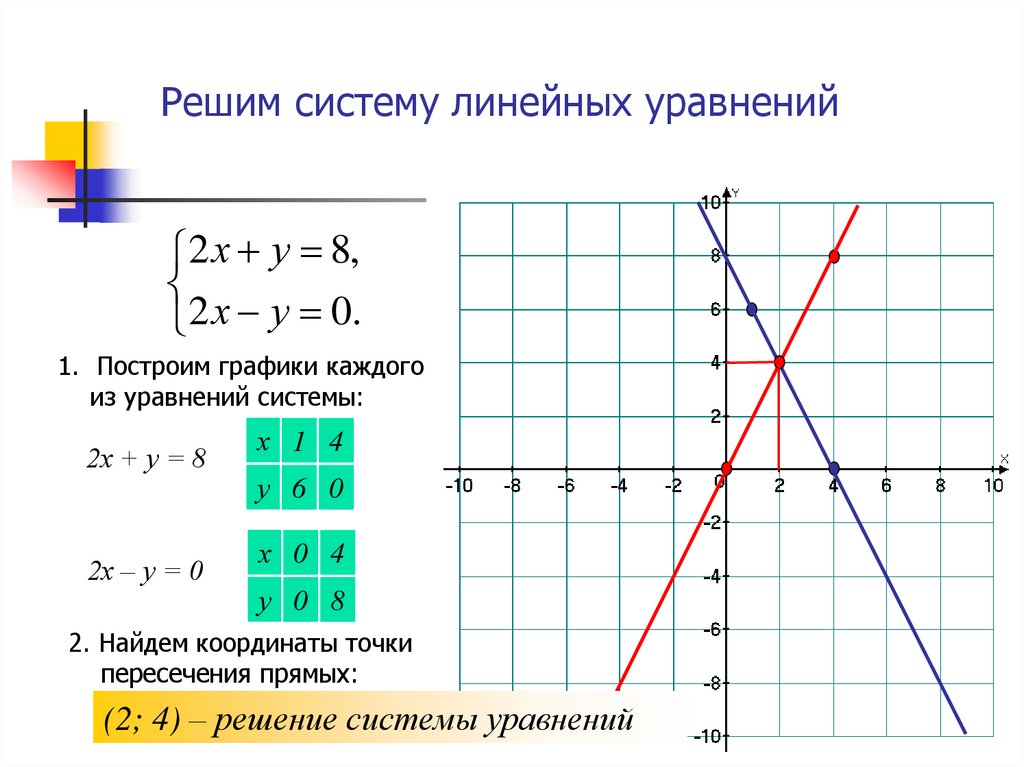
y = x ² – x – 6. Красная линия представляет график г = к. Сопоставьте каждый график с уравнением, перетащив график в соответствующий слот. Затем укажите правильные решения, представленные на графике, перетащив правильные упорядоченные пары в поле решения.
Видео
Просмотрите следующее видео, чтобы узнать больше о решении квадратного уравнения.
Источник
Оценка функций с помощью графического калькулятора, Gdawy Enterprises, You Tube
Практика
Найдите решение каждого квадратного уравнения с помощью графика.
График представляет собой полезное представление для определения решения квадратного уравнения. Чтобы лучше использовать график, представьте, что квадратное уравнение состоит из двух частей: a x ² + b x + c = k
Нарисуйте график каждой части квадратного уравнения: a x ² + b x + с = к и y = k
Найдите пересечение двух графиков. Координаты точек пересечения x сообщат вам значения x , которые являются решениями исходного уравнения.
Например, график f( x ) = −0,25 x ² + 0,5 x + 3,75 показан ниже. Вы можете использовать график для определения решений связанного уравнения −0,25 x ² + 0,5 x
Вы также можете использовать график для решения уравнения -0,25 x ² + 0,5 x + 3,75 = 0 путем определения точки пересечения x , поскольку ось x совпадает с линией y = 0.
- Печать
- Поделиться
| |||||
| | |||||
| Графическое решение Если есть пара цифр, которые можно заменить на x и y в двух разных уравнениях, пара образует координаты точки, лежащей на графике. каждый уравнение. Единственный способ, которым точка может лежать на двух линий одновременно, чтобы точка находилась на пересечении линий. Таким образом, графическое решение двух одновременные уравнения включают в себя рисование их графиков и найти точку, в которой линии графика пересекаются.Например, когда мы рисуем уравнения x+y=33 и x-y = 5, как и на рисунке 12-5, мы видим, что они пересекаются в одной точке. Есть одна пара значения, содержащие координаты этого точка (19, 14), и эта пара значений удовлетворяет обоим уравнениям следующим образом:Рисунок 12-5.-График x + y = 33 и x — y = 5. Эта пара чисел удовлетворяет каждому уравнению. Это единственная пара чисел, удовлетворяющая двум уравнения одновременно. Перекресток выглядит так
точка (4, 7). Подставляя x = 4 и y = 7 в
уравнений показывает, что это фактическая точка
пересечение, так как эта пара чисел удовлетворяет обоим уравнениям.Рисунок 12-6 – График x + у = 11 и х — у = -3. Уравнения 7x — 8y = 2 и 4x + 3y = 5 являются изображено на рис. 12-7. Линии пересекаются там, где у примерно 1/2, а x примерно 5/6. Практические задачи. Решите графически следующие одновременные системы: Метод добавления Метод сложения решения систем уравнений показано в следующем примере: Получен результат предыдущего примера добавлением левого члена первого уравнения к левому члену второго и прибавляя правый член первого уравнения справа член второй. Найдя значение x, подставляем это значение в любом из исходных уравнений к найдите значение y следующим образом: Обратите внимание, что основная цель дополнения
метод заключается в устранении (временно) одного
переменных. | |||||
