Как найти периметр квадрата 4 класс формула: Как найти периметр квадрата 🟩 формула

Периметр квадрата и периметр прямоугольника в 1-4 классах

Во многих задачах для правильного решения очень важно построить схематический чертеж. В Задаче 1 с ребенком обязательно стоит обсудить, почему квадраты нужно располагать именно таким образом. Что за фигура получится, если взаимное расположение квадратов будет иным (прямоугольника вообще не выйдет!)? При вычислении периметра полученного прямоугольника обязательно обратите внимание ученика на то, то вычисления в уме можно произвести более рационально, если сначала прибавить 12 и 18 (получится 30), а потом просто удвоить результат.

Важно вовремя научить ребенка считать устно, чтобы он мог видеть быстрые и легкие способы вычислений. Как правило, взрослому человеку привить такое умение гораздо сложнее. Если школьник сам не заметил, как рациональнее делаются вычисления, то не стоит прерывать его подсчеты. Только когда ребенок назовет ответ, нужно показать ему этот замечательный способ. Если вдруг у ученика самостоятельные подсчеты вызывают затруднения ,то стоит уму показывать только один способ, а потом, когда тот его усвоит, нужно научить школьника и второму. Это позволит избежать путаницы в вычислениях у ученика.

В Задаче 2 можно обсудить с ребенком вопрос о том, когда квадрат превращается в прямоугольник. Что такое квадрат, что такое прямоугольник? Чем квадрат похож на прямоугольник? В чем их существенная разница.

Задача 3 очень хороша тем, что дает возможность поразмышлять, рассмотреть разные способы, которыми можно отрезать квадрат от прямоугольника. При разрезе могло получиться 2 фигуры – квадрат 6х6 и прямоугольник 2х6, а могло получиться и 3 фигуры — квадрат 6х6 и 2 прямоугольника с длиной 6, а ширина будет завесить от того в каком месте вырезали квадрат.

Задача 1: Прямоугольник составлен из трех квадратов, стороны которых равны 6 см, 12 см и 6 см. Найдите периметр этого прямоугольника.

Решение: opened=0

Из трех квадратов, которые подходят в условие задачи, можно составить прямоугольник так, как показано на рисунке.

Получается, сто его стороны будут 6 см + 6 см = 12 см и 6 см + 12 см = 18 см.

Периметр такого прямоугольника 12 см + 12 см + 18 см + 18 см = 12 см + 18 см + 12 см + 18 см = 30 см + 30 см = 60 см.

Задача 2: Сравните периметры прямоугольника и квадрата, если сторона квадрата.   Причем эта сторона больше ширины прямоугольника на 2 см и меньше его длины на 3 см.

Решение: opened=0

Найдем периметр квадрата 6 см + 6 см + 6 см + 6 см 24 см.

Найдем ширину прямоугольника 6 см – 2 см = 4 см.

Найдем длину прямоугольника 6 см + 3 см = 9 см.

Найдем периметр прямоугольника 4 см + 4 см + 9 см + 9 см = 26 см.

Периметр прямоугольника больше, чем периметр квадрата на 26 см – 24 см = 2 см.

Задача 3: От прямоугольника со сторонами 8 см и 6 см отрезали квадрат со стороной 6 см. Чему равен периметр оставшейся фигуры.

Задача 4: Периметр квадрата 28 см. Найти периметр такого прямоугольника, ширина которого равна стороне этого квадрата, а его длина в 2 раза больше его ширины?

Задача 5: Ширина прямоугольника 10 см, а его длина 16 см. Начертите квадрат, с периметром в 2 раза меньше периметра прямоугольника.

Если вы желаете узнать, как решаются эти, другие более сложные или легкие задачи по геометрии для школьников, то обращайтесь к администратору сайта Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.. Мы поможем вам совершенно бесплатно!

Памятка «Площадь и периметр квадрата и прямоугольника» | Методическая разработка по математике (2 класс) по теме:

Опубликовано 14.03.2013 — 19:25 — Черненко Анна Анатольевна

Памятка «Площадь и периметр квадрата и прямоугольника»

Скачать:

Предварительный просмотр:

Площадь прямоугольника S=a*b где  S – площадь,        а – длина,        b – ширина Отсюда:                         а = S : b                         b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2           Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4

Площадь прямоугольника S=a*b где  S – площадь,        а – длина,        b – ширина Отсюда:                         а = S : b                         b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2           Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4

Предварительный просмотр:

Площадь прямоугольника S=a*b где  S – площадь,        а – длина,        b – ширина Отсюда:                         а = S : b                         b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2           Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4

Площадь прямоугольника S=a*b где  S – площадь,        а – длина,        b – ширина Отсюда:                         а = S : b                         b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2           Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4

Предварительный просмотр:

Площадь прямоугольника S=a*b где  S – площадь,        а – длина,        b – ширина Отсюда:                         а = S : b                         b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2           Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4

Площадь прямоугольника S=a*b где  S – площадь,        а – длина,        b – ширина Отсюда:                         а = S : b                         b = S : a Периметр прямоугольника P=a+a+b+b=a*2+b*2 или Р=(а+b)*2           Отсюда: а = (Р — b) : 2 b= (P — a) : 2 Периметр и площадь квадрата S=a*a P= a*4

По теме: методические разработки, презентации и конспекты

Периметр квадрата и прямоугольника.

Сценарий урока.

Сценарий урока математики по теме: «Периметр квадрата и прямоугольника» 2 класс по программе «Школа 2100″….

Периметр квадрата и прямоугольника. Презентация.

Презентация к уроку по математике по теме: «Периметр квадрата и прямоугольника» 2 класс программа «Школа 2100″…

Урок математики во 2 классе.Периметр квадрата и прямоугольника.

Цели урока (Ц): обобщить, систематизировать, открыть новые знания о квадрате и прямоугольнике, о нахождении периметра этих фигур.Ожидаемые результаты урока:Предметный: формирование навыка изображения …

Урок математики во 2 классе Тема: Периметр квадрата и прямоугольника

Урок математики во 2 классе Тема: Периметр квадрата и прямоугольника…

Технологическая карта урока математики по теме «Формулы периметра квадрата и прямоугольника»

Технологическая карта урока математики по теме «Формулы периметра квадрата и прямоугольника»УМК системы развивающего обучения Л.В. Занкова, 2 классРазработка включает в себя технологиче. ..

Задачи «Периметр квадрата и прямоугольника»

Данный материал позволяет  учащимся закрепить и твёрдо усвоить тему «Периметр  квадрата и прямоугольника». Тренажёр можно использовать для проведения проверочных работ по данной те…

Периметр квадрата и прямоугольника

Конспект урока  математики ….

Поделиться:

 

Рабочие листы по периметру квадратов

Пусть наши бесплатные печатные рабочие листы по периметру квадратов станут вашим надежным маяком, пока вы выполняете ряд упражнений по нахождению периметра квадратов. Учащиеся могут не только решать иллюстративные задачи, включающие целые числа, десятичные числа или дробные длины сторон, но и мгновенно проверять результаты, используя прилагаемые ключи ответов. Наши рабочие листы по периметру квадрата доступны как в обычных, так и в метрических единицах измерения.

Эти инструменты в формате PDF настоятельно рекомендуются для учащихся 2-х, 3-х, 4-х и 5-х классов.

Выберите единицы измерения Традиционные единицы США Метрические единицы

Периметр квадратов — целые числа | Уровень 1. Рабочий лист №1

Сложите длины всех сторон, чтобы найти периметр квадрата. Поскольку все четыре стороны квадрата имеют одинаковую длину, периметр в четыре раза больше длины данной стороны.

Периметр квадратов — Целые числа | Уровень 1 — Рабочий лист № 2

Нахождение периметра квадрата конституционно просто! Этот удобный для начинающих рабочий лист с целыми числами < 20 единиц в качестве боковых мер делает его еще проще для детей 2-го и 3-го классов!

Периметр квадратов — Целые числа | Уровень 2. Рабочий лист №1

Попросите учащихся заменить «а» на заданную длину стороны в формуле периметр квадрата = 4а. Дети будут стремиться к большему, как только они решат этот печатный периметр квадратного листа.

Периметр квадратов — Целые числа | Уровень 2. Рабочий лист №2

Найти длину контура квадрата несложно! Доступный для бесплатного использования, этот умеренно сложный PDF-инструмент позволяет ребенку сохранять спокойствие, когда он сталкивается с целыми числами до 100 единиц в качестве дополнительных мер.

Периметр квадратов — дроби | Рабочий лист №1

Помогите учащимся 4 и 5 классов определить заданную длину стороны, выраженную в виде дробей, по соответствующей формуле и с точностью вычислить периметр квадрата.

Периметр квадратов — дроби | Рабочий лист № 2

Позвольте детям обосновать свое обучение, решив все 9 упражнений на этом периметре квадратного рабочего листа в формате PDF. С нашими искусно проиллюстрированными задачами процесс вряд ли будет казаться рутиной.

Периметр квадратов — Десятичные дроби | Рабочий лист №1

Посмотрите, как нетерпеливые бобры собираются толпами, чтобы решить этот печатный ресурс! Дети решают задачи с размерами сторон, представленными десятичными знаками, и изучают веревки.

Периметр квадратов — Десятичные дроби | Рабочий лист № 2

Учащиеся 5-го класса получают дополнительную практику и учатся умножать заданную длину стороны на четыре, чтобы определить периметр каждого квадрата, используя эту распечатку.

Найдите длину стороны квадрата по периметру. Рабочие листы

Эта эксклюзивная коллекция бесплатных рабочих листов в формате PDF добавит детям массу удовольствия и ценности. Посмотрите, как юные гении вычисляют длину стороны квадрата, используя заданный периметр в каждом упражнении.

Площадь и периметр квадратов Рабочие листы

Этот раздел наших печатных рабочих листов помогает лучше понять концепцию периметра квадрата. Попробуйте и посмотрите, как дети уверенно решают задачи на площадь и периметр квадратов.

Как найти периметр квадрата (3 вещи, которые нужно знать) — JDM Educational

Периметр квадрата говорит нам, как далеко нам придется пройти, чтобы обойти квадрат, идя вдоль каждой стороны и поворачиваясь на 90 градусов в углы. Полезно знать, как найти периметр квадрата, зная информацию о квадрате.

Итак, как найти периметр квадрата? Квадрат со стороной S имеет периметр 4S (это получается из сложения всех четырех сторон, каждая из которых имеет длину S).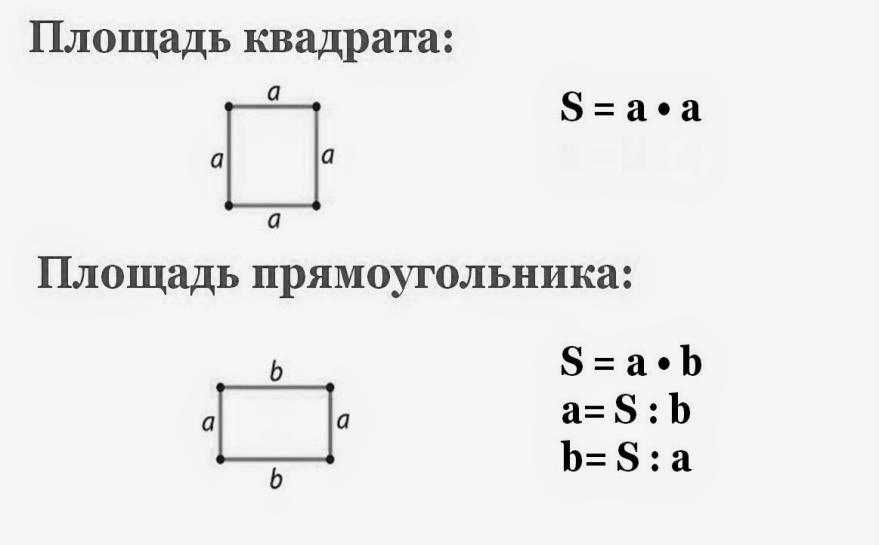 Длина стороны и периметр всегда указываются в линейных единицах (например, в футах или дюймах). Чтобы найти длину стороны S квадрата с периметром P, мы делим P на 4, чтобы получить S = P/4.

Конечно, мы также можем найти периметр квадрата, зная его площадь, диагональ или другую информацию.

В этой статье мы поговорим о том, как найти периметр квадрата и рассмотрим несколько примеров. Мы также ответим на некоторые распространенные вопросы о периметрах квадратов.

Начнем.

Как найти периметр квадрата

Чтобы найти периметр квадрата, нам нужно знать длину стороны или найти ее по имеющейся у нас информации.

Если мы знаем длину стороны квадрата S (или если мы можем найти ее из предоставленной нам информации), то мы можем найти периметр P.

Помните: у квадрата четыре стороны одинаковой длины и четыре угла по 90 градусов. Это означает, что нам нужна только длина одной стороны квадрата, и мы знаем длины всех сторон.

Начнем с самого простого случая: нахождения периметра квадрата по длине его стороны.

Как найти периметр квадрата с длиной стороны

Если у нас есть длина стороны квадрата, то легко найти периметр. Для квадрата со стороной S периметр P определяется по формуле:

• P = 4S [формула для периметра квадрата]

Квадрат со стороной S имеет периметр 4С.

Обратите внимание, что S (длина стороны квадрата) и P (периметр квадрата) даны в линейных единицах, например:

• Футы (футы)
• Дюймы (дюймы)
• Метры (м)

Рассмотрим на примере, как найти периметр квадрата, зная длину стороны.

Пример: Найдите периметр квадрата по длине стороны

Допустим, у нас есть квадрат со стороной 5 футов.

Тогда S = 5 футов, и мы можем использовать это в формуле для периметра P квадрата:

• P = 4S   [формула для периметра квадрата]
• P = 4(5) [единицы для S — футы]
• P = 20 футов

Итак, периметр квадрата со стороной 5 футов равен 20 футам.

Квадрат со стороной 5 футов имеет периметр 20 футов (4*5 = 20).

Как найти периметр квадрата с площадью

Помните, что квадрат со стороной S имеет площадь A = S ² . Это получается путем умножения ширины на высоту (каждая из них имеет одинаковую длину S):

• A = S*S = S ²

Квадрат со стороной S имеет площадь S ² .

Мы также можем работать в обратном порядке, чтобы найти длину стороны S из площади A. Все, что нам нужно сделать, это извлечь квадратный корень:

• A = S ²
• √A = S
9
9 Поскольку мы знаем периметр P через S, мы можем найти периметр и через площадь:
• P = 4S   [формула для периметра квадрата]
• P = 4(√A)   [решено для длины стороны, S, через площадь, A]
• P = 4√A

квадрат с площадью A.

Обратите внимание, что мы также можем работать в обратном порядке, чтобы найти площадь A из периметра P, решив:

• P = 4√A   [формула для периметра P через площадь A]
• P ² = 16A
• P ² /16 = A

Давайте рассмотрим пример того, как найти периметр квадрата, зная его площадь.

Пример: Найдите периметр квадрата площадью

Допустим, у нас есть квадрат площадью 36 квадратных футов.

Тогда A = 36 квадратных футов, и мы можем использовать это в формуле для периметра P квадрата, которую мы нашли выше:

• P = 4√A   [формула для периметра P в единицах площади A]
• P = 4√(36)   [единицы измерения А — футы]
• P = 4*6 футов
• P = 24 фута

Итак, периметр квадрата площадью 36 квадратных футов равен 24 футам.

Квадрат площадью 36 квадратных футов имеет длину стороны 6 футов и, следовательно, периметр 4*6 = 24 фута.

Мы также можем проверить нашу работу, найдя длину стороны S. Для квадрата площадью 36 футов длина стороны будет S = √A = √36 = 6 футов.

Квадрат со стороной S = 6 футов будет иметь периметр P = 4S = 4(6) = 24 фута. Это соответствует тому, что мы нашли выше.

Как найти периметр квадрата с диагональю

Помните, что квадрат со стороной S имеет диагональ D = S√2.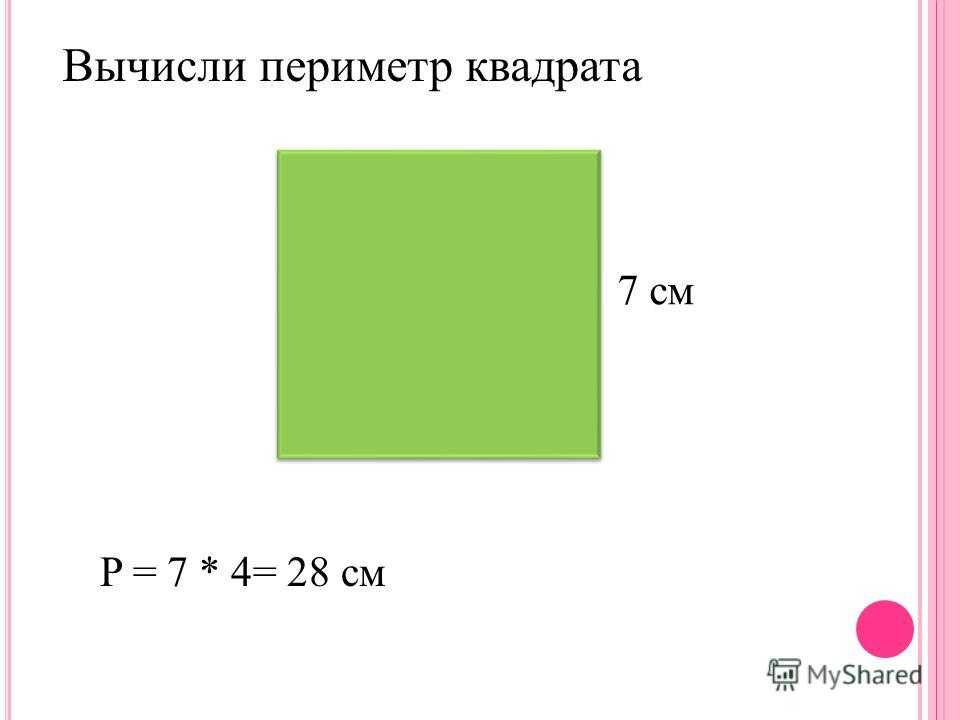 Это происходит из использования теоремы Пифагора для одного из прямоугольных треугольников (половина квадрата с диагональю в качестве гипотенузы):

Квадрат с диагональю D и длиной стороны S
удовлетворяет уравнению D = S√2.
• а ² + b ² = с ²   [Теорема Пифагора]
• S ² + S ² = D ²   [катеты a и b — длина стороны S квадрата, а c — диагональ D]
• 2S ² = D ²  [соединить подобные термины]
• √(2S ² ) = D [извлечь квадратный корень из обеих сторон]
• S√2 = D   [упрощенно]

Это также означает, что мы можем найти длину стороны S найти:

• S√2 = D
• S = D/√2

Поскольку мы знаем периметр P через S, мы можем найти периметр и через диагональ:

• P = 4S   [формула для периметра квадрата]
• P = 4 (D/√2)   [решено для длины стороны, S, через диагональ, D]
• P = 4√2(D/2)  [рационализировать знаменатель]
• P = (2√2 )D

В предыдущей строке находится формула периметра P квадрата с диагональю D.

Обратите внимание, что мы также можем работать в обратном порядке, чтобы найти диагональ D из периметра P, решив:

• P = (2√2)D [формула для периметра P через диагональ D]
• P/ (2√2) = D
• √2P/(2*2) = D [рационализировать знаменатель]
• √2P/4 = D

Давайте посмотрим на примере, как найти периметр квадрата по диагонали.

Пример: Найдите периметр квадрата по диагонали

Допустим, у нас есть квадрат с диагональю 10 футов.

Тогда D = 10 футов, и мы можем использовать это в формуле для периметра P квадрата, которую мы нашли выше:

• P = (2√2)D D]
• P = (2√2)(10)  [единицы для D — футы]
• P = 20√2 фута

Итак, — диагональ квадрата с периметром 10 футов это 20√2 футов (около 28 футов).

Квадрат с диагональю 10 футов и длиной
имеет периметр 20√2 фута.

Мы также можем проверить нашу работу, найдя длину стороны S. Для квадрата с диагональю 10 футов длина стороны будет S = D/√2 = 10/√2 = (10√2)/2 = 5. √2 фута.

Квадрат со стороной S = 5√2 фута будет иметь периметр P = 4S= 4(5√2) = 20√2 фута. Это соответствует тому, что мы нашли выше.

Как найти периметр квадрата, вписанного в круг

Когда вы вписываете квадрат в круг, вы действительно ищете самый большой квадрат, который едва помещается внутри круга. Вы также можете думать об этом как о наименьшем возможном круге, который едва содержит квадрат.

Этот сценарий показан на изображении ниже.

Здесь мы видим самый большой квадрат, который может поместиться внутри круга
(или самый маленький круг, который может содержать квадрат).

Мы можем найти взаимосвязь между этими двумя формами и их размерами следующим образом.

Пусть S — длина стороны квадрата, а R — радиус окружности.

Сначала проведем диаметр от левого нижнего угла квадрата до левого верхнего угла. Это дает нам диагональ с длиной R + R = 2R (диаметр круга).

Обозначим стороны квадрата буквой S (как показано на схеме ниже).

Диагональ квадрата в два раза больше радиуса (диаметра) круга, или 2R. Длины сторон также отмечены на прямоугольном треугольнике.

На данный момент у нас есть прямоугольный треугольник, две короткие стороны (катеты) которого имеют длину S и S, с гипотенузой 2R (диаметр окружности). Используя теорему Пифагора, получаем:

• a ² + b ² = c ²   [a и b — длины сторон, c — гипотенуза]
+
S ² = (2R) ²   [длины обеих сторон равны S, а гипотенуза или диагональ равны 2R, диаметру круга]
• 2S ² = 4R ² [Combine Like Terms]
• S ² = 2R ² [раздел на 2]
98
• 9005 3 9005

2 ² . обеих сторон]

Это уравнение дает нам связь между радиусом R круга и длиной стороны S квадрата.

Это говорит нам о том, что длина стороны квадрата S будет примерно на 41% больше, чем радиус круга (√2 составляет около 1,41 в виде десятичной дроби).

Периметр квадрата равен P = 4S = 4 ( R√2) = (4√2)R.

Давайте рассмотрим пример.

Пример: как найти периметр квадрата с вписанным в него кругом

Предположим, что у нас есть квадрат, вписанный в круг, как указано выше. Круг имеет диаметр 12 футов.

Это означает, что радиус (половина диаметра) равен 12/2 = 6 футов. Итак, R = 6 футов.

Теперь мы можем использовать найденную выше формулу для периметра P квадрата, вписанного в круг:

• P = (4√2)R   [площадь квадрата, вписанного в круг радиуса R]
• P = (4√2)(6)   [R = 6 футов]
• P = 24√2 фута
• P ~ 34 фута

Квадрат, вписанный в круг диаметром 12 футов
, имеет периметр 24√2 квадратных фута.

Как найти длину стороны квадрата, зная периметр

Чтобы найти длину стороны квадрата, зная периметр, нам просто нужно разделить периметр на 4.

Помните, что периметр квадрата со стороной S равен P = 4S.

Разделив обе части уравнения на 4, мы получим P/4 = S.

Пример. Найдите длину стороны квадрата по периметру

Допустим, у нас есть квадрат с периметром 84 фута.

Тогда P = 84, и мы можем найти длину стороны S по формуле, которую мы нашли выше:

• S = P/4
• S = 84/4  [P = 84 фута]
• S = 21 фут

Квадрат с периметром 84 квадратных фута
имеет длину стороны 21 фут.

Что означает периметр квадрата?

Периметр квадрата в основном говорит нам о расстоянии вокруг внешнего края квадрата. Другими словами, сколько вам придется пройти, чтобы обойти площадь.

Могут ли периметр и площадь квадрата быть одинаковыми?

В некоторых случаях периметр и площадь квадрата могут иметь одно и то же числовое значение.

Однако единицы всегда разные, так как:

• Периметр имеет линейные единицы (футы, дюймы, метры и т. д.)
• Площадь имеет квадратные единицы (квадратные футы, квадратные дюймы, квадратные метры и т. д.)

Используем формулу для периметра и площадь квадрата, чтобы узнать, когда они имеют одинаковое значение.

Вспомните, что для квадрата со стороной S:

• Периметр = P = 4S
• Площадь = A = S ²

Таким образом, когда площадь и площадь равны:

• Perimeter = Area
• 4S = S ²
• 0 = S ² – 4S
• 0 = S(S – 4)
• S = 0 or S = 4

Итак, возможны два случая, когда периметр и площадь квадрата имеют одно и то же значение:

• S = 0 (тривиальный квадрат без площади, с нулевыми длинами сторон и периметром)
• S = 4 (квадрат со стороной 4 единицы)

Итак, квадрат со стороной 4 фута будет иметь периметр 4*4 = 16 футов и площадь 4 ² = 16 квадратных футов.

No related posts.