Теория игр: Введение / Хабр
Что это такое, и с чем его едят.
Теория игр — это раздел математической экономики, изучающий решение конфликтов между игроками и оптимальность их стратегий. Конфликт может относиться к разным областям человеческого интереса: чаще всего это экономика, социология, политология, реже биология, кибернетика и даже военное дело. Конфликтом является любая ситуация, в которой затронуты интересу двух и более участников, традиционно называемых игроками. Для каждого игрока существует определенный набор стратегий, которые он может применить. Пересекаясь, стратегии нескольких игроков создают определенную ситуацию, в которой каждый игрок получает определенный результат, называемый выигрышем, положительным или отрицательным. При выборе стратегии важно учитывать не только получение максимального профита для себя, но так же возможные шаги противника, и их влияние на ситуацию в целом.
Краткая история развития.
Основы теории игр зародились еще в 18 веке, с началом эпохи просвящения и развитием экономической теории.
Впервые математические аспекты и приложения теории были изложены в классической книге 1944 года Джона фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение». Первые концепции теории игр анализировали антагонистические игры, когда есть проигравшие и выигравшие за их счет игроки. Не смотря на то, что теория игр рассматривала экономические модели, вплоть до 50-х годов 20 века она была всего лишь математической теорией. После, в результате резкого скачка экономики США после второй мировой войны, и, как следствие, большего финансирования науки, начинаются попытки практического применения теории игр в экономике, биологии, кибернетике, технике, антропологии. Во время Второй мировой войны и сразу после нее теорией игр серьезно заинтересовались военные, которые увидели в ней мощный аппарат для исследования стратегических решений. В начале 50-х Джон Нэш (на фото) разрабатывает методы анализа, в которых все участники или выигрывают, или терпят поражение. Эти ситуации получили названия «равновесие по Нэшу».
Как это работает
Как мне кажется, смысл теории игр проще всего пояснить на «Дилемме заключенного», классическая формулировка которой звучит так:
Двое преступников, А и Б, попались примерно в одно и то же время на сходных преступлениях.Есть основания полагать, что они действовали по сговору, и полиция, изолировав их друг от друга, предлагает им одну и ту же сделку: если один свидетельствует против другого, а тот хранит молчание, то первый освобождается за помощь следствию, а второй получает максимальный срок лишения свободы (10 лет). Если оба молчат, их деяние проходит по более лёгкой статье, и они приговариваются к 6 месяцам. Если оба свидетельствуют против друг друга, они получают минимальный срок (по 2 года). Каждый заключённый выбирает, молчать или свидетельствовать против другого. Однако ни один из них не знает точно, что сделает другой. Что произойдёт?
Есть основания полагать, что они действовали по сговору, и полиция, изолировав их друг от друга, предлагает им одну и ту же сделку: если один свидетельствует против другого, а тот хранит молчание, то первый освобождается за помощь следствию, а второй получает максимальный срок лишения свободы (10 лет). Если оба молчат, их деяние проходит по более лёгкой статье, и они приговариваются к 6 месяцам. Если оба свидетельствуют против друг друга, они получают минимальный срок (по 2 года). Каждый заключённый выбирает, молчать или свидетельствовать против другого. Однако ни один из них не знает точно, что сделает другой. Что произойдёт?
Представив игру в виде матрицы мы получим:
| Преступник Б Стратегия «молчать» |
Преступник Б Стратегия «предать» |
|
|---|---|---|
| Преступник А Стратегия «молчать» |
Пол года каждому | 10 Лет преступнику А Отпустить преступника Б |
| Преступник А Стратегия «предать» |
10 Лет преступнику Б Отпустить преступника А |
2 года каждому |
А теперь представим развитие ситуации, поставив себя на место заключенного А.
Типы игр
Кооперативная\некооперативная игра
Кооперативной игрой является конфликт, в котором игроки могут общаться между собой и объединяться в группы для достижения наилучшего результата. Примером кооперативной игры можно считать карточную игру Бридж, где очки каждого игрока считаются индивидуально, но выигрывает пара, набравшая наибольшую сумму. Из двух типов игр, некооперативные описывают ситуации в мельчайших деталях и выдают более точные результаты. Кооперативные рассматривают процесс игры в целом. Не смотря на то, что эти два вида противоположны друг другу, вполне возможно объединение стратегий, которое может принести больше пользы, чем следование какой-либо одной.
С нулевой суммой и с ненулевой суммой
Игрой с нулевой суммой называют игру, в которой выигрыш одного игрока равняется проигрышу другого. Например банальный спор: если вы выиграли сумму N, то кто-то эту же сумму N проиграл. В игре же с ненулевой суммой может изменяться общая цена игры, таким образом принося выгоду одному игроку, не отнимаю ее цену у другого. В качестве примера здесь отлично подойдут шахматы: превращая пешку в ферзя игрок А увеличивает общую сумму своих фигур, при этом не отнимая ничего у игрока Б. В играх с ненулевой суммой проигрыш одного из игроков не является обязательным условием, хотя такой исход и не исключается.
Параллельные и последовательные
Параллельной является игра, в которой игроки делают ходы одновременно, либо ход одного игрока неизвестен другому, пока не завершится общий цикл. В последовательной игре каждый игрок владеет информацией о предидущем ходе своего оппонента до того, как сделать свой выбор.
С полной или неполной информацией
Эти типы являются подвидом последовательных игр, и названия их говорят сами за себя.
Метаигры
Эти игры являются «леммами» теории игр. Они полезны не сами по себе, а в контексте какого-либо конфликата, расширяя его набор правил.
В любом конфликте типы объединяются, определяя таким образом правила игры, будь это кооперативная последовательная игра с нулевой суммой, или метаигра с неполной информацией.
Проблемы практического применения
Безусловно, следует указать и на наличие определенных границ применения аналитического инструментария теории игр. В следующих случаях он может быть использован лишь при условии получения дополнительной информации.
Во-первых, это тот случай, когда у игроков сложились разные представления об игре, в которой они участвуют, или когда они недостаточно информированы о возможностях друг друга.
Например, может иметь место неясная информация о платежах конкурента (структуре издержек). Если неполнотой характеризуется не слишком сложная информация, то можно применять опыт подобных случаев с учетом определенных различий.
Во-вторых, теорию игр трудно применять при множестве ситуаций равновесия. Эта проблема может возникнуть даже в ходе простых игр с одновременным выбором стратегических решений.
В-третьих, если ситуация принятия стратегических решений очень сложна, то игроки часто не могут выбрать лучшие для себя варианты. Например, на рынок в разные сроки могут вступить несколько предприятий или реакция уже действующих там предприятий может оказаться более сложной, нежели быть агрессивной или дружественной.
Экспериментально доказано, что при расширении игры до десяти и более этапов игроки уже не в состоянии пользоваться соответствующими алгоритмами и продолжать игру с равновесными стратегиями.
К сожалению, ситуации реального мира зачастую очень сложны и настолько быстро изменяются, что невозможно точно спрогнозировать, как отреагируют конкуренты на изменение тактики.
Тем не менее, теория игр полезна, когда требуется определить наиболее важные и требующие учета факторы в ситуации принятия решений в условиях конкурентной борьбы. Эта информация важна, поскольку позволяет учесть дополнительные переменные или факторы, имеющие возможность повлиять на ситуацию, и тем самым повысить эффективность решения.
Заключение
Если тема окажется интересной для сообщества, следующих статьях я попытаюсь подробнее раскрыть типы игр и их стратегии.
от холодной войны до пенальти — ECONS.ONLINE
Фрагмент картины Александра Дейнеки «Вратарь», 1934 г.
Фото: deineka.ru
Мнения
Экономика
Поведенческая экономика
Теория игр дает экономистам возможность браться за анализ самых разных областей, и хотя она далеко не всегда позволяет сделать точное предсказание, с ее помощью можно выявить стратегии действия и выигрыши участников в зависимости от того или иного исхода.
4 марта 2020 | Андрей Бремзен
Теория игр дает экономистам возможность браться за анализ самых разных областей, и хотя она далеко не всегда позволяет сделать точное предсказание, с ее помощью можно выявить стратегии действия и выигрыши участников в зависимости от того или иного исхода.
4 марта 2020 | Андрей Бремзен
Если спросить у непредвзятого человека: «Про что, как ты думаешь, теория игр?» – то почти наверняка все игры, которые он назовет, окажутся играми с нулевой суммой, они еще называются антагонистическими. Шахматы – классический пример игры с нулевой суммой. В шахматах разыгрывается одно очко, либо выигрывают белые 1:0, либо черные 0:1, либо ничья – по 1/2 очка. Все, что белые выиграли, черные проиграли: каждое очко, каждую половинку очка. Это всегда один против другого.
Равновесие по Нэшу
Равновесием по Нэшу называется такая ситуация, когда никому из игроков не выгодно менять свою стратегию в отдельности, то есть стратегия каждого – наилучшая реакция на решения других участников. Лауреат Нобелевской премии по экономике 1994 г. за исследования в области теории игр математик
Джон Нэш доказал, что такое равновесие существует в любой конечной игре, если игроки могут применять смешанные стратегии, то есть не придерживаться одного и того же выбора в любой ситуации, а обладать набором различных решений, из которых он может выбрать.
На основе биографии Джона Нэша «Игры разума», изданной в 1998 г., был поставлен одноименный фильм с Расселом Кроу в главной роли.
Такие игры хорошо исследованы: можно, например, доказать, что в каждом из равновесий Нэша (см. врез) тот или иной игрок получает один и тот же «платеж» (то есть условный выигрыш). То есть если в каком-то равновесии платеж первого игрока равен, например, двум, то и в любом другом равновесии он тоже равен двум. Таким образом, исход игры с нулевой суммой настолько предсказуем, насколько на предсказуемость вообще можно надеяться – ясно, кто из игроков в среднем выигрывает, а кто проигрывает, и сколько.
Игрой с нулевой суммой часто ошибочно считают международную торговлю. Например, американский обыватель часто считает, что если Китай богатеет благодаря торговле с США, если Китаю это выгодно, то по определению это означает, что Америка от этого теряет. «Если им выгодно с нами торговать, значит, они крадут у нас рабочие места», – так обычно говорят в таких случаях.
На самом деле международная торговля – это, конечно, игра с ненулевой суммой, то есть игра, в которой выигрыш могут получить оба игрока (и получают, в той мере, в которой участие в международной торговле является добровольным). В теории международной торговли легко доказать, что если вы «маленькая» страна на том или ином рынке – в том смысле, что у вас нет надежды повлиять на мировую цену на тот или иной товар, – то нужно немедленно отменить импортные пошлины на этот товар. Ими вы наказываете только себя.
С точки зрения экономической теории наибольший интерес представляют как раз игры с ненулевой суммой, но тут предсказания куда менее однозначны.
Как найти место встречи
Говорить о таких играх удобно начать с класса игр, которые можно назвать «играми координации», то есть такими играми, в которых интересы игроков полностью совпадают. В каком-то смысле это игры, противоположные по своим свойствам играм с нулевой суммой. Если в антагонистических играх выигрыш одного игрока всегда равен проигрышу другого (здесь и далее мы рассматриваем только игры с двумя игроками), то в координационных играх выигрыш одного равен выигрышу другого.
В самом простом случае эти выигрыши равны либо оба единице, либо оба нулю. Можно представить себе такую ситуацию: вам нужно встретиться с незнакомым человеком в Москве. Вы зафиксировали дату, но не успели договориться о времени и месте. У вас есть фотография этого человека и, главное, понимание, что он тоже хочет с вами встретиться. Куда и к которому часу следует прийти, чтобы с максимальными шансами встреча состоялась? У этого вопроса нет «правильного» ответа, нет «оптимальной» стратегии: мы считаем, что «платеж» будет одинаковым независимо от того, в какой точке и в какой момент игроки встретятся, – лишь бы они встретились.
Я много лет задаю эту задачу студентам – прошу написать время и место на листе бумаги. Подавляющее большинство выбирает полдень (на втором месте с большим отрывом – 18 часов). И опять же подавляющее большинство выбирает Красную площадь. В Москве, таким образом, легко идентифицируется так называемая «фокальная точка» – такое выделенное место, которое всем кажется наиболее подходящим для встречи.
К сожалению, эта особенность Москвы не транслируется автоматически на другие города, особенно такие, про которые игрок может мало что знать (или не ожидать от партнера, что тот много знает), – попробуйте, например, Якутск или Будапешт. Таким образом, даже для координационных игр предсказательная сила теории невелика. Тем более безнадежной выглядит задача в общем случае игры с ненулевой суммой.
Классический пример такой игры – «семейный спор». Муж и жена должны, не сговариваясь, выбрать одно из двух развлечений на вечер – футбол или балет. Выигрыш – два очка за компанию плюс одно очко за любимое развлечение. Таким образом, если оба выбирают футбол, жена получает 2 очка (только компания), а муж 2+1=3 очка (компания плюс любимое развлечение), если оба – балет, то наоборот. Если муж выбирает футбол, а жена – балет, то они получают по одному очку, а если наоборот – никто ничего не получает. Здесь сразу видны два равновесия (оба выбирают футбол, или оба – балет), но теория не дает никаких оснований предпочесть какое-то одно из них.
Теория игр с ненулевой суммой приобрела особенную актуальность во время холодной войны между СССР и США. Это очевидная игра с ненулевой суммой – с того момента, как каждая из сторон получила достаточное количество оружия, чтобы уничтожить жизнь на всей планете, стало ясно, что, несмотря на очевидное соперничество, обе стороны заинтересованы в том, чтобы избежать вооруженного конфликта, – в этом цели игроков совпадали. Но при этом каждая из сторон продолжала быть заинтересованной в том, чтобы максимально расширить сферу своего влияния, – и в этом цели игроков были противоположными. Ситуация осложнялась тем, что в случае обострения конфликта решение требовалось принимать практически моментально. Человечество впервые в своей истории оказалось поставленным в такие условия, что это спровоцировало рост интереса к теоретико-игровым исследованиям.
Важнейшей работой, посвященной теоретическому анализу холодной войны, является вышедшая в 1960 г. книга Томаса Шеллинга «Стратегия конфликта».
Впоследствии Шеллинг получил за нее Нобелевскую премию по экономике (потому что традиционно теория игр является частью именно экономической науки). Я всячески рекомендую эту книгу каждому, кто интересуется теорией стратегических взаимодействий, но ни в этой книге, ни в дальнейшем развитии теории игр не удалось добиться убедительных предсказаний исхода в играх с ненулевой суммой.
Обычно предсказания теории игр тестируют в лаборатории, и таких экспериментов сделано гигантское количество. Но со всеми этими экспериментами всегда возникают одни и те же проблемы. Люди могут плохо понять правила или иметь недостаточную мотивацию хорошо играть в лабораторных условиях – например, из-за скромного размера обещанного вознаграждения. Поэтому чрезвычайную ценность при тестировании предсказаний теории игр на данных, и в частности предсказаний о смешанных равновесиях, имеют ситуации, которые происходят за пределами лаборатории, но в которых люди играют в похожие игры.
Футбол – это такая ситуация. Причем не просто футбол – это слишком сложная игра. Конкретно один момент в нем, а именно 11-метровый удар. Один на один выступают игрок, пробивающий по воротам, и вратарь. В отличие от участников лабораторных экспериментов, и у тренеров, и у нападающих, и у вратарей есть достаточно времени, чтобы потренироваться, то есть «изучить правила». Во-вторых, у всех игроков крупных серьезных матчей, а мы говорим именно о таких, достаточно мотивации, так как часто на кону стоят большие суммы призовых. Наконец, пенальти проще изучать, потому что там не так уж много стратегий.
Можно предположить, что тот, кто бьет по воротам (особенно если речь идет о серии пенальти в конце матча), может ударить либо прямо, либо в левый угол, либо в правый, причем прямо – крайне редко, это можно игнорировать. Мяч летит со скоростью около 300 км/ч, время от нанесения удара до пересечения лицевой линии мячом – примерно 0,2 секунды. За это время у вратаря нет возможности проследить за направлением полета мяча и прыгнуть в нужную сторону, это подтверждают сами вратари в многочисленных интервью.
Нужно принимать решение, прыгать налево или направо, и определиться раньше, чем противник ударит по мячу. Таким образом, вырисовывается ясная картина: у одного есть возможность пробить в левый или в правый угол, у второго – броситься в левый или в правый угол. Получаем антагонистическую игру, близкую к «камень, ножницы, бумага».
Как я уже сказал выше, для игр с нулевой суммой как раз есть убедительное предсказание. Каждый, кто играл в «камень, ножницы, бумага», знает, как надо действовать: надо быть максимально непредсказуемым. На языке теории игр это называется «смешанной стратегией»: каждый из трех ходов надо выбирать с положительной вероятностью. Более того, можно доказать, что вероятность каждого хода должна быть одинаковой – по одной трети. Если вы будете выбирать что-то одно, вы проиграете.
Аналогично и с пенальти: если вы всегда бьете в левый от себя угол и вратарь это знает, он бросится туда. Конечно, забить гол все равно можно, при условии что вы ударили по мячу со страшной силой – тогда вратарь не спасет.
Но шансы намного больше, чем если вы ударите слабее, но в другой угол. То есть задача такая же, как в «камень, ножницы, бумага»: быть непредсказуемым.
Играют ли футболисты в смешанные стратегии, и если да, то с правильными ли весами? На эту тему почти одновременно (в 2002 и 2003 гг.) вышли две статьи в самых авторитетных экономических журналах, они популярно описаны в захватывающей книге «Футболономика» Саймона Купера и Стефана Шимански. Теория предсказывает, что с вероятностью 58% нужно бить в левый от себя угол, если вы правша. А в данных мы видим 57,7%. И так пробивают люди, которые никогда не изучали смешанные стратегии!
Один мой профессор (вероятно, цитируя кого-то из великих) высказал как-то поразившую меня мысль: экономика – скорее тип мышления, чем наука. Во всяком случае, экономисты смело берутся за такие разные области, как холодная война и футбол, главное – применять принятые стандарты метода, в данном случае – теории игр.
Статья основана на лекции «Почему экономика – это не только про экономический рост и совсем не про бухучет» из цикла лекций Совместного бакалавриата РЭШ и ВШЭ
«Больше, чем экономика».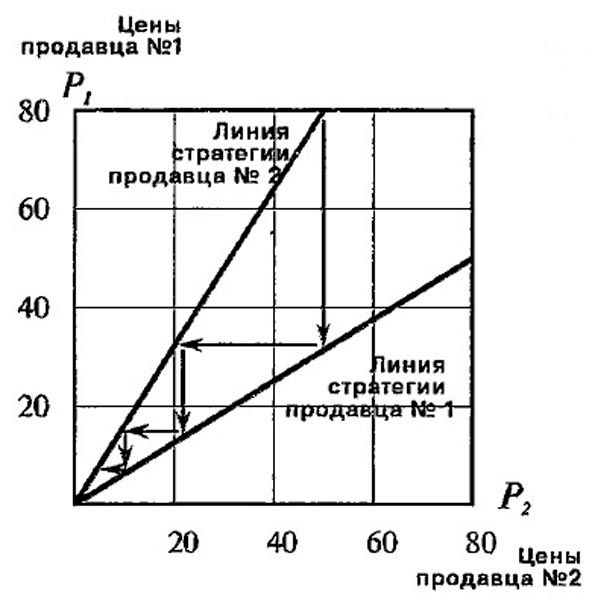
Андрей Бремзен
Профессор РЭШ
Самое популярное
Теория гравитации в экономике: выводы для России
Старые проблемы новых активов
Как предприятия Ирана адаптировались к санкциям
Юань: нетрадиционный путь к статусу резервной валюты
Мошенники и их жертвы: кто уязвим и почему
Сколько стоит время
Андрей Бремзен
Профессор РЭШ
Самое популярное
Теория гравитации в экономике: выводы для России
Старые проблемы новых активов
Как предприятия Ирана адаптировались к санкциям
Юань: нетрадиционный путь к статусу резервной валюты
Мошенники и их жертвы: кто уязвим и почему
Сколько стоит время
Примеры теории игр в экономике
Теджван Петтингер
Исследование игр — это изучение стратегического взаимодействия, когда решение одного игрока зависит от действий другого игрока. То, что делает противник, также зависит от того, что, по его мнению, сделает первый игрок.
- Доминирующая стратегия – когда один выбор дает лучший результат, чем другой
- Равновесие по Нэшу — когда каждый игрок ничего не выигрывает, меняя стратегию, учитывая выбор другого игрока. Равновесие Нэша не обязательно является эффективным по Парето. Оба игрока могут выиграть от сотрудничества.
Ценовая война
Это аналогичный результат, но для двух фирм, которые могут поддерживать высокие и стабильные цены или начать ценовую войну. Наилучший результат для обеих фирм: (а) 40 долл., 40 долл.
Однако, когда цены стабильны, если одна фирма снизит цены (начнет ценовую войну), ее прибыль вырастет до 60 долларов.
Однако другая фирма, поддерживающая высокие цены, потеряет долю рынка и получит нулевую прибыль. Следовательно, проигравшая фирма почти наверняка примет ответные меры, и результат изменится на (d), когда обе фирмы получат только 3 доллара прибыли. Следовательно, существует сильный стимул избегать ценовой войны.
- Координация плей-офф
- В этом примере, если ни одна из фирм не инвестирует, каждая из них получит по 50 долларов. Однако, если они оба инвестируют в новую технологию, которая станет новым рыночным стандартом, они оба получат значительно большую отдачу (а) по 200 долларов каждый.
- Однако, если одна фирма инвестирует в новую технологию, а другая нет, то у них останется 0 долл. (эта сумма широко не распределяется). В этом случае фирма, вероятно, тоже начнет инвестировать, так как им будет лучше.
- Однако ключевой вопрос заключается в том, готова ли одна фирма сделать решительный шаг и получить нулевую прибыль в краткосрочной перспективе. Это может быть не в состоянии позволить себе такой результат.
- Проблема с этой дилеммой по теории игр заключается в том, что сотрудничество приносит большие выгоды. Но в реальном мире по разным причинам сотрудничества может и не быть.
Это может быть не в состоянии позволить себе такой результат.Совпадающие монеты
- В этой игре участвуют два игрока. Они оба положили пенни на стол.
- Если монеты выпадают орлом/орлом или решкой/решкой, то игрок А выигрывает обе монеты. Он получает 1 (игрок Б теряет 1)
- Если монеты смешанные (орел/решка) или решка/орел, то при игре В выигрываются обе монеты.
- Это пример игры с нулевой суммой – чистый выигрыш всегда равен нулю. Для каждого, кто выигрывает, есть равный и противоположный проигрыш.
Игра с нулевой суммой
В этой ситуации мы имеем другую ситуацию с игрой с нулевой суммой. Если фирма входит или уходит, чистая выгода всегда равна нулю.
Основной стратегией фирмы А является выход на рынок, поскольку 1 больше -2.
Для фирмы B доминирующей стратегией также является выход на рынок, поскольку -1 больше, чем -3. Фирма B предпочла бы, чтобы обе фирмы ушли с рынка, чтобы она могла достичь нуля. Но в этой модели он не может этого сделать, потому что знает, что если А войдет, ему придется войти или столкнуться с затратами -3.
Тарифы или торговая война?
- В этом случае, если обе страны будут придерживаться низких тарифов, результатом будет 3 миллиона фунтов чистого благосостояния для каждой страны. Если А установит тариф, то ее чистое благосостояние составит 2 млн фунтов стерлингов, а страна Б, сохраняющая низкие тарифы, получит 1,5 млн фунтов стерлингов.
- Если B примет ответные меры и введет пошлины, это ухудшит положение самого себя – благосостояние упадет до 1 млн фунтов стерлингов, но это эффективно накажет А, чье благосостояние упадет с 2 млн фунтов стерлингов до 1 млн фунтов стерлингов.
- Если фирмы хотят максимизировать благосостояние, они будут придерживаться низких тарифов. Это их доминирующая стратегия и равновесие Нэша.
- Однако в реальном мире может иметь место политическое давление (например, защита отечественной промышленности даже за счет более высоких цен для потребителей, что побуждает страны устанавливать тарифы9).0012
Это их доминирующая стратегия и равновесие Нэша.Дилемма заключенного
Дилемма заключенного — классический пример теории игр.
- В одиночной камере содержатся двое заключенных. Они могут либо признаться в преступлении, либо промолчать (не признаться)
- Если оба будут хранить молчание, то оба получат легкий срок в 1 год.
- Если оба сознаются, каждый получает по 5 лет.
- Однако, если один сознается в преступлении и выдает другого, то тому, кто сознается, дается неприкосновенность за дачу информации. А тот, кто промолчал, получает 20 лет.
- Таким образом, заключенный предпочтет хранить молчание только в том случае, если он может гарантировать, что другой заключенный будет хранить молчание.
- Главной стратегией для обоих игроков является признание. В худшем — 5 лет, в лучшем — 0 лет.
- Равновесие Нэша – это признание/признание (по 5 лет каждый). Потому что, если бы игрок действовал в одностороннем порядке, ему было бы хуже.
Дерево решений
Другой способ описания теории игр — дерево решений.
- В этом примере фирма А может войти или выйти. Фирма B (затем действующий оператор может принять решение бороться (снижать цены) или приспособиться.
- В случае конфликта обе фирмы проигрывают (-4, -3). Таким образом, доминирующей стратегией фирмы В является приспособление, в результате чего обе фирмы получают (1,1) .
- Однако фирма B может сделать расчет, что стоит понести временные убытки, чтобы попытаться заставить новую фирму выйти из бизнеса. Кроме того, если фирма B будет бороться, это может отпугнуть других участников рынка.
- См. также: Теория игр – сдерживание входа
Дерево решений
В этом дереве решений игрок 1 может двигаться вверх или вниз.
- Если игрок 1 идет вверх, доминирующей стратегией для игрока 2 является повышение (3,5)
- Если игрок 1 опускается, доминирующая стратегия игрока 2 состоит в том, чтобы подняться выше (10,4)
- Следовательно, игрок 1 выберет низкий уровень, потому что он знает, что это лучший выбор.
Доминирующая стратегия
Доминирующая стратегия возникает, когда существует оптимальный выбор стратегии для каждого игрока независимо от того, что делает другой.
- Если P2 выберет лево, P1 выберет UP
- Если P2 сделает правильный выбор, P1 выберет UP
- Следовательно, UP является доминирующей стратегией для P1
- P2 всегда будет делать правильный выбор независимо от того, что делает P1
- Уникальное равновесие (вверху, влево). Это лучше для обоих.
Равновесие Нэша
Равновесие Нэша возникает, когда выигрыш первого игрока является наилучшим при выборе другого.
- В этом случае Если P1 выбирает вниз, P2 выбирает вправо
- Если P1 выберет ВВЕРХ, P2 выберет право. Но, если P2 выбирает правильно, P1 захочет выбрать вниз.
- Равновесие Нэша будет прямолинейным (5,5), несмотря на то, что ВВЕРХ слева является оптимальным исходом по Парето.
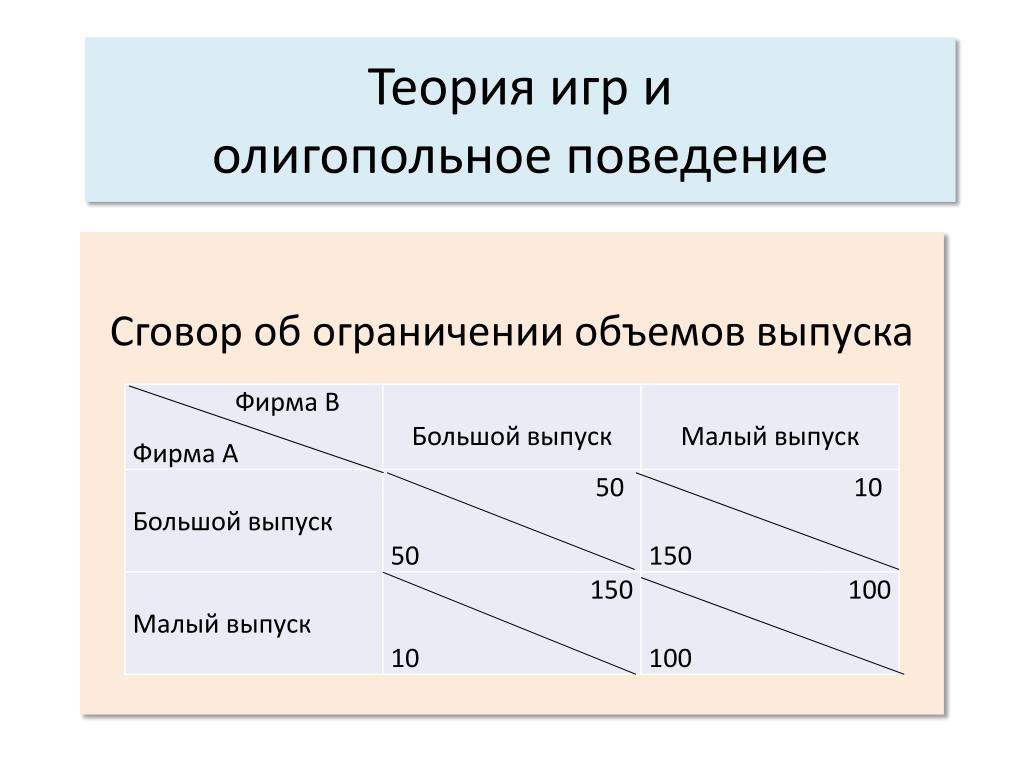
Сговор и теория игр
- Если фирмы конкурентоспособны и устанавливают низкие цены, они обе заработают по 4 млн.
- Если они вступят в сговор и установят высокую цену, то они оба удвоят свою прибыль и заработают 8 миллионов фунтов стерлингов.
- Однако, если во время сговора фирма А сбивает сговорившуюся цену и устанавливает низкую цену – она способна продать больше. В этом случае фирма А извлекает выгоду из лучшего из обоих миров. Цены высоки, потому что фирма B устанавливает высокую цену, но фирма A также продает большие объемы, потому что она уступает конкуренту. В этом случае фирма А зарабатывает 10 млн фунтов стерлингов, а фирма В — только 2 млн фунтов стерлингов.
- Следовательно, маловероятно, что фирма B будет поддерживать высокие цены, и рынок вернется к установлению низких цен обеими сторонами.
Оптимальным исходом для фирм является сговор (высокая цена, высокая цена)
Повторные игры и теория игр
Если игры повторяются, то есть возможность наказать людей за мошенничество, это даст стимул придерживаться Парето-оптимальный подход.
Однако, если они будут повторяться конечное число раз, появится стимул к обману. Если игра сыграна 10 раз, то игрок сбежит в 10-м раунде, так зачем сотрудничать. Таким образом, вы также можете дезертировать в 9-м раунде.и так 8 раунд тоже
Если играть бесконечное количество раз, то он будет другим. Тогда лучшая стратегия — играть «око за око». Если игрок отказывается в одном раунде, вы принимаете ответные меры в следующем раунде. Другими словами, вы делаете то, что делает ваш оппонент, и это является стимулом для усиления картеля.
Теория игр: игра сдерживания входа
Если на рынок выходит новая фирма, то выигрыш будет зависеть от того, будет ли действующая фирма сопротивляться или соглашаться. Если действующий оператор борется, они оба получают 0. Если он не борется, то действующий оператор получает 1, а новичок получает 2. Следовательно, равновесие состоит в том, что новая фирма входит, а действующий оператор принимает.
Однако, если действующий президент может дать правдоподобную угрозу, что он будет драться, он может убедить участника остаться в стороне. Он мог бы сделать это, инвестируя в дополнительные мощности, что дало бы ему больший выигрыш в ценовой войне. Это будет препятствовать входу. Таким образом, хотя монополист никогда не воспользуется этим, он предотвратит вход.
Теория игр и изогнутая кривая спроса
Теория игр может быть использована для стратегий ценообразования
В условиях олигополии фирмы могут решать, следует ли снизить цены, повысить цены или оставить их неизменными.
Модель изогнутой кривой спроса предполагает, что наиболее вероятным результатом будет стабильность цен. Это связано с тем, что
- Если фирмы повышают цену, а другие нет, то спрос значительно падает. (спрос эластичен)
- Если фирмы снизят цены, вы получите увеличение доли рынка. Другие фирмы не хотят этого допускать. Поэтому они и снижают цены. В основном вызывает ценовую войну, в которой все проигрывают.
Таким образом, в условиях олигополии важной характеристикой решений фирм является влияние взаимозависимости. Решения одной фирмы существенно влияют на другие.
Война против мира
В этом случае лучший результат для обеих сторон — Мир, Мир (a) — обе получают 100. Однако, если вы думаете, что может быть война, лучше нанести удар первым. Потому что, если вы нанесете удар первым и начнете войну, вы получите 50, а проигравший — 50. из лучшей стратегии для обоих.
Родственные
- Теория игр — снижение цен на PlayStation
Как это работает в теории игр, примеры, плюс дилемма заключенного
Что такое равновесие Нэша?
Равновесие по Нэшу — это концепция теории игр, согласно которой оптимальный исход игры достигается при отсутствии стимула отклоняться от первоначальной стратегии. В частности, равновесие по Нэшу — это концепция теории игр, согласно которой оптимальный результат игры — это такой, при котором ни у одного игрока нет стимула отклоняться от выбранной стратегии после рассмотрения выбора противника.
В целом, человек не может получить дополнительную выгоду от изменения действий, если предположить, что другие игроки остаются неизменными в своих стратегиях. В игре может быть несколько равновесий Нэша или вообще не быть ни одного.
Ключевые выводы
- Равновесие Нэша — это теорема принятия решений в рамках теории игр, которая утверждает, что игрок может достичь желаемого результата, не отклоняясь от своей первоначальной стратегии.
- В равновесии Нэша стратегия каждого игрока оптимальна при рассмотрении решений других игроков. Каждый игрок выигрывает, потому что каждый получает желаемый результат.
- Дилемма заключенных — распространенный пример из теории игр, который адекватно демонстрирует эффект равновесия Нэша.
- Равновесие Нэша часто обсуждается в связи с доминирующей стратегией, которая утверждает, что выбранная действующим лицом стратегия приведет к лучшим результатам из всех возможных стратегий, которые могут быть использованы, независимо от стратегии, используемой противником.
- Равновесие Нэша не всегда означает выбор наиболее оптимальной стратегии.
Равновесие Нэша
Понимание равновесия Нэша
Равновесие Нэша названо в честь его изобретателя Джона Нэша, американского математика. Это считается одним из наиболее важных понятий теории игр, которая пытается математически и логически определить действия, которые должны предпринять участники игры, чтобы обеспечить себе наилучшие результаты.
Причина, по которой равновесие Нэша считается таким важным понятием теории игр, связана с его применимостью. Равновесие Нэша может быть включено в широкий спектр дисциплин, от экономики до социальных наук.
Чтобы быстро найти равновесие Нэша или проверить, существует ли оно вообще, раскройте стратегию каждого игрока другим игрокам. Если никто не меняет свою стратегию, то равновесие Нэша доказано.
Равновесие Нэша против доминирующей стратегии
Равновесие Нэша часто сравнивают с доминирующей стратегией, поскольку обе стратегии являются стратегиями теории игр. Равновесие по Нэшу утверждает, что оптимальная стратегия для актора состоит в том, чтобы придерживаться курса своей первоначальной стратегии, зная стратегию противника, и что все игроки придерживаются одной и той же стратегии, пока все остальные игроки не изменят свою стратегию.
Доминирующая стратегия утверждает, что выбранная субъектом стратегия приведет к лучшим результатам из всех возможных стратегий, которые можно использовать, независимо от стратегии, используемой противником.
Все модели теории игр работают только в том случае, если вовлеченные игроки являются «рациональными агентами», что означает, что они желают конкретных результатов, действуют, пытаясь выбрать наиболее оптимальный результат, включают неопределенность в свои решения и реалистичны в своих вариантах.
Оба термина похожи, но немного отличаются. Равновесие Нэша утверждает, что ничего не выиграет, если один из игроков изменит свою стратегию, если все остальные игроки сохранят свою стратегию. Доминирующая стратегия утверждает, что игрок выберет стратегию, которая приведет к наилучшему результату, независимо от стратегий, выбранных другими игроками. Доминирующая стратегия может быть включена в равновесие Нэша, тогда как равновесие Нэша может быть не лучшей стратегией в игре.
Пример равновесия Нэша
Представьте себе игру между Томом и Сэмом. В этой простой игре оба игрока могут выбрать стратегию А, чтобы получить 1 доллар, или стратегию Б, чтобы проиграть 1 доллар. Логически оба игрока выбирают стратегию А и получают выигрыш в размере 1 доллара.
Если вы раскрыли стратегию Сэма Тому и наоборот, вы увидите, что ни один игрок не отклоняется от первоначального выбора. Знание хода другого игрока мало что значит и не меняет поведения ни одного из игроков. Результат A представляет собой равновесие Нэша.
Особые соображения
Дилемма заключенного — это обычная ситуация, анализируемая в теории игр, в которой может использоваться равновесие Нэша. В этой игре двое преступников арестованы, и каждый содержится в одиночной камере, не имея возможности общаться друг с другом. У прокуратуры нет улик, чтобы осудить эту пару, поэтому они предлагают каждому заключенному возможность либо предать другого, дав показания о том, что другой совершил преступление, либо сотрудничать, храня молчание.
Если оба заключенных предадут друг друга, каждый отбывает по пять лет тюрьмы. Если A предает B, но B хранит молчание, заключенный A освобождается, а заключенный B отбывает 10 лет тюрьмы или наоборот. Если каждый промолчит, то каждый отбывает всего по году тюрьмы.
Равновесие Нэша в этом примере состоит в том, что оба игрока предают друг друга. Хотя взаимное сотрудничество приводит к лучшему результату, если один заключенный выбирает взаимное сотрудничество, а другой нет, результат одного заключенного хуже.
Часто задаваемые вопросы о равновесии Нэша
Что такое равновесие Нэша в теории игр?
Равновесие Нэша в теории игр — это ситуация, в которой игрок будет продолжать придерживаться выбранной стратегии, не имея стимула отклоняться от нее, приняв во внимание стратегию противника.
Как найти равновесие Нэша?
Чтобы найти равновесие Нэша в игре, нужно смоделировать каждый из возможных сценариев, чтобы определить результаты, а затем выбрать оптимальную стратегию. В игре с двумя людьми это будет учитывать возможные стратегии, которые могут выбрать оба игрока. Если ни один из игроков не меняет свою стратегию, зная всю информацию, наступило равновесие Нэша.
Почему равновесие Нэша важно?
Равновесие Нэша важно, потому что оно помогает игроку определить наилучший выигрыш в ситуации, основываясь не только на своих решениях, но и на решениях других вовлеченных сторон. Равновесие Нэша можно использовать во многих сферах жизни, от бизнес-стратегий до продажи дома войне и социальных наук.
Как рассчитать равновесие Нэша?
Не существует конкретной формулы для расчета равновесия Нэша, но его можно определить путем моделирования различных сценариев в данной игре, чтобы определить выигрыш каждой стратегии и выбрать оптимальную стратегию.
Каковы ограничения равновесия Нэша?
Основное ограничение равновесия Нэша заключается в том, что оно требует, чтобы человек знал стратегию своего противника. Равновесие Нэша может возникнуть только в том случае, если игрок решит остаться со своей текущей стратегией, если он знает стратегию своего противника.
В большинстве случаев, например, на войне, будь то военная война или война на торгах, человек редко знает стратегию противника или то, каким он хочет видеть результат. В отличие от доминирующей стратегии, равновесие Нэша не всегда приводит к наиболее оптимальному результату, оно просто означает, что человек выбирает наилучшую стратегию на основе имеющейся у него информации.
Кроме того, в нескольких играх с одними и теми же противниками равновесие Нэша не принимает во внимание прошлое поведение, которое часто предсказывает будущее поведение.