Самостоятельные работы
Самостоятельная работа 9кл урок 8
Вариант 1
1. Начертите неколлинеарные вектора а, b, с . Постройте векторы а + с, с – b.
2. В равнобедренном треугольнике АВС точка В1 – середина основания АС.
а) Упростите выражение ВВ1 – АВ – В1С.
б) Найдите / ВВ1 – АВ – В1С / , если АВ=10см, ВВ1= 8см.
3. Найдите вектор РО – х = РМ
Самостоятельная работа 9кл урок 8
Вариант 2
1. Начертите неколлинеарные вектора p, k, с . Постройте векторы k+ с, k – p.
2. В равнобедренном треугольнике АВС , с основанием АВ проведена медиана СС1
а) Упростите выражение ВС1 – АС + АВ,
б) Найдите / ВС1— АС + АВ /, если АС=5см, АВ=6см.
3. Найдите вектор х – МА =РМ
Самостоятельная работа 9кл урок 10 стр 54
Вариант 1.
1. Начертите вектор х такой что, /х /= 2см. Постройте векторы 3 х, -2 х, 1/2х,
2. В параллелограмме АВСД на стороне АВ отмечена точка К так, что АК:КВ= 2:1, О- точка пересечения диагоналей. Выразите векторы ОС и СК через векторы а=АВ, и b= АД.
Самостоятельная работа 9кл урок 10 стр 54
Вариант 2.
1. Начертите вектор а , абсолютная величина которого равна 3см. Постройте векторы 2а , -а, 1/3а.
2. В параллелограмме АВСД на стороне ВС взята точка Р так, что ВР:РС=3:1 , О- точка пересечения диагоналей . Выразите векторы АО и РА через векторы х=АВ и у=АД.
Самостоятельная работа 9кл урок 8
Вариант 1
1. Начертите неколлинеарные вектора а, b, с . Постройте векторы а + с, с – b.
2. В равнобедренном треугольнике АВС точка В1 – середина основания АС.
а) Упростите выражение ВВ 1 – АВ – В1С.
б) Найдите / ВВ1 – АВ – В1С / , если АВ=10см, ВВ1= 8см.
3. Найдите вектор РО – х = РМ
Самостоятельная работа 9кл урок 8
Вариант 2
1. Начертите неколлинеарные вектора p, k, с . Постройте векторы k+ с, k – p.
2. В равнобедренном треугольнике АВС , с основанием АВ проведена медиана СС1
а) Упростите выражение ВС1 – АС + АВ,
б) Найдите / ВС1— АС + АВ /, если АС=5см, АВ=6см.
3. Найдите вектор х – МА =РМ
Самостоятельная работа 9кл урок 10 стр 54
Вариант 1.
1. Начертите вектор х такой что, /х /= 2см. Постройте векторы 3 х, -2 х, 1/2х,
2. В параллелограмме АВСД на стороне АВ отмечена точка К так, что АК:КВ= 2:1, О- точка пересечения диагоналей. Выразите векторы ОС и СК через векторы а=АВ, и b= АД.
Самостоятельная работа 9кл урок 10 стр 54
Вариант 2.
1. Начертите вектор а , абсолютная величина которого равна 3см. Постройте векторы 2а , -а, 1/3а.
Постройте векторы 2а , -а, 1/3а.
2. В параллелограмме АВСД на стороне ВС взята точка Р так, что ВР:РС=3:1 , О- точка пересечения диагоналей . Выразите векторы АО и РА через векторы х=АВ и у=АД.
Урок 21 Геометрия 9кл
Самостоятельная работа
1 вариант
1.Окружность задана уравнением (х+5)2+(у-4)2=49.
а) Укажите центр окружности
б) Какие из точек А(2;4), В(1;3), С(-5;-3) лежат на данной окружности.
в) Найдите точку с абциссой -12 , лежащей на данной окружности.
2. Напишите уравнение окружности с центром С и радиусом r: если
а) С(-3;2), r= √ 3 . б) С(0;-6) , r= 4√5.
Самостоятельная работа 9 класс 27урок
- Найдите sinA, если 1 вариант cosA= -1/3 2 вариант cosA=-1/4
2.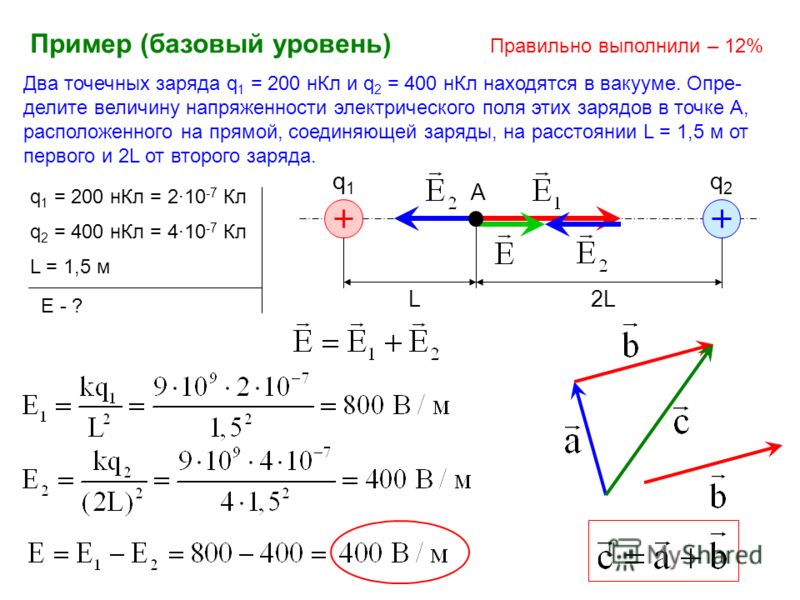 Найдите cosA, если 1 вариант sinA= 2/5 2вариант sinA=-2/3
Найдите cosA, если 1 вариант sinA= 2/5 2вариант sinA=-2/3
- Проверьте, лежат ли на единичной окружности точки:
1 вариант В(7;3),С(0,5;0,5) 2 вариант С(2;3), В(-0,5;0,5)
4. Угол между лучом ОМ, пересекающим единичную полуокружность, и положительной полуосью Ох равен А. Найдите координаты точки М, если
1 вариант ОМ=8, <А=30°
Самостоятельная работа 9кл
По теме : Решение треугольников
1. Дано: △АВС , <А=450 , < С=150 , ВС= 4√6 .
Найти: АВ , АС , < В
2. Дано : △MNK , MN=6см , MK=10см, <M=1200.
Найти : NK , <N , <K.
3. Дано : △ ОРТ , ОР=24 , РТ=30, ОТ=36.
Найти: <О , <Р, <Т.
Самостоятельная работа 9 кл урок 33
Тема Решение треугольников
1 вариант
1. Площадь параллелограмма равна 30V3 см2, а один из углов равен 600. Найдите его периметр, если длина одной из сторон равна 6см.
2. В треугольнике MNK MN=NK , MK=V2 , <M=30 0, MA- ,биссектриса. Найдите МА.
3. Стороны треугольника равны 8, 10 и 12см. Найдите угол, лежащий против меньшей стороны.
Самостоятельная работа 9 кл урок 33
Тема Решение треугольников
2 вариант
1. Площадь параллелограмма равна 40V2 см2 , а один из углов равен 450 . Найдите его периметр , если длина одной из сторон равна 10см.
2. В треугольнике СДЕ СМ- биссектриса , <ДСЕ=600 , МЕ= 3V2. Найдите СМ, если < СЕД =450.
3. Стороны треугольника равны 6, 9 и 10 см. Найдите угол , лежащий против большей стороны.
Найдите угол , лежащий против большей стороны.
Самостоятельная работа 9кл. по геометрии
По теме Правильный многоугольник
1. Найдите углы правильного шестнадцатиугольника .
2. Каждый угол правильного многоугольника равен 162
3. Чему равен внешний угол правильного восемнадцатиугольника .
4. Внешний угол правильного многоугольника равен 150.Найдите число его сторон.
5. Является ли равнобедренный треугольник с углом при вершине в 600 правильным.
6. Является ли ромб с равными диагоналями правильным четырехугольником .
Самостоятельная работа по геометрии 9кл
По теме Формулы для вычисления площади правильного многоугольника его стороны и радиуса вписанной окружности.
Вариант 1
1. Найдите углы правильного восемнадцатиугольника .
2. Угол правильного n-угольника равен 1080. Вычислите количество его сторон .
Вычислите количество его сторон .
3. Сколько сторон имеет правильный вписанный многоугольник , если дуга описанной окружности , которую стягивает его сторона , равна 45 0.
Урок 44 9класс стр 228
Самостоятельная работа
1 вариант
1. Найдите длину окружности с радиусом 5см. Чему равна длина ее дуги с градусной мерой 360.
2. Длина окружности, описанной около квадрата , равна 12П см. Найдите длину окружности, вписанной в этот квадрат.
Урок 44 9класс стр 228
Урок геометрии в 9-м классе
- Архипова Любовь Ивановна
Разделы: Математика
Тема: «Умножение вектора на число».
Цель урока: совершенствовать навыки решения задач на применение свойств умножения вектора на число, развивать логическое мышление.
Ход урока
Презентация
I. Организационный момент
II. Актуализация знаний обучающихся
1. Фронтальный опрос:
а) дайте определение вектора;
б) какие векторы называются коллинеарными;
в) какой вектор называется произведением данного вектора на данное число;
г) чему равно произведение , если: а) = ; б) k=0?
д) могут ли векторы а и ka быть неколлинеарными?
е) сформулируйте основные свойства умножения вектора на число.
2. Устное решение задач на готовых чертежах.
Карточки для индивидуальной работы
I уровень (карточка № 1)
1. Даны два неколлинеарных вектора и построить:
а) ; б) 2; в) + 2.
2. Дано: АВСD – параллелограмм, = , = . Выразите , , через и
II уровень (карточка № 2)
1. Дан треугольник АВС. Построить векторы:
а) + ; б) — — .
2 Дано: АВСD – параллелограмм, = , = . Выразите , ,, через и
III. Решение задач
1. Повторить свойства умножения вектора на число.
2. Решение задач:
а) № 781
б)
в)
IV.Самостоятельная работа
I уровень
Вариант 1
1. Начертит вектор такой, что ││= 2 см. Постройте векторы 3; -2; .
2. В параллелограмме АВСД на стороне АВ отмечена точка К так, что АК:КВ = 2:1 О – точка пересечения диагоналей. Выразите векторы и через векторы = и = .
Вариант 2
1. Начертите вектор , абсолютная величина которого равна 3 см. Постройте векторы 2; -; .
2. В параллелограмме АВСД на стороне ВС отмечена точка Р так, что ВР :РС = 3 :1 О – точка пересечения диагоналей. Выразите векторы и через векторы = и = .
Выразите векторы и через векторы = и = .
II уровень
1. Начертите два неколлинеарных вектора и так, что ││= 2 см. и ││= 3 см. Постройте вектор — 2.
2. На сторонах ВС и СД параллелограмма АВСД взяты соответственно точки М и Е так, что М – середина ВС, СЕ : ЕД =1 :3. Выразите векторы , , через векторы = и = .
V. Подведение итогов урока
Оценить работу учащихся на уроке.
VI. Домашнее задание
I уровень: № 782, 784(б), 787;
II уровень: № 782, 784(в), 785
ВЕКТОРОВ — КРАТКОЕ ОБУЧЕНИЕ
ВЕКТОРОВ — КРАТКОЕ ОБУЧЕНИЕ ВЕКТОРЫ — КРАТКОЕ РУКОВОДСТВОI. Вы можете описать вектор, за наших целей тремя способами, как показано ниже.
1. Опишите, указав величину (число и единицу измерения) и направление (угол, измеренный против часовой стрелки от оси + x ).
Здесь d = 3 см при 115 o .
( Примечание : «Хвост» вектора не обязательно должен располагаться в
источник.)
2. Опишите, указав координаты x и y . из «голова» и «хвост» вектора.
3. Опишите, указав компонентов вектора. Здесь:
d x = d cosq
= (3 см)(cos115 o ) = -1,27 см d y = д sinq
= (3 см)(sin115 о ) = 2,72 см
( d есть
модуль, то есть абсолютное значение, вектора d .)
Для ясности в
на векторной диаграмме две прямые проходят через вектор, когда он
заменены
по его компонентам.
II. минус вектор
имеет ту же величину, что и исходный вектор, но угол направления
поворачивается на 180 o .
В
пример, показанный выше, — d = 3 см при 295 o .
III. Добавление вектора.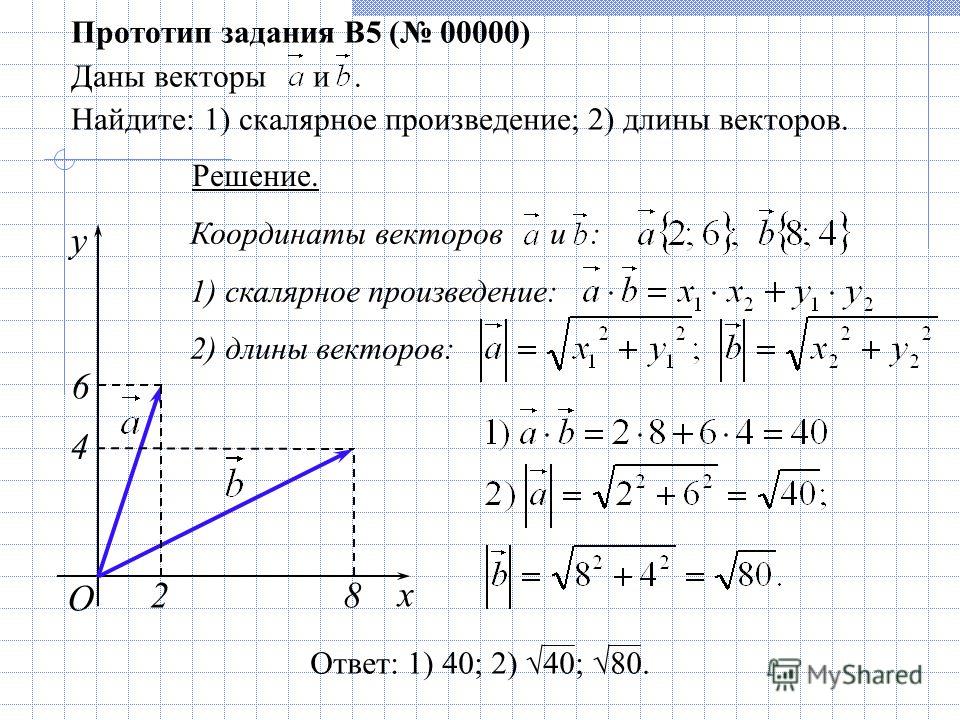
- 1. Чтобы добавить два или более вектора графически ,
использовать метод «голова к хвосту». Измерьте сумму (также называемую результирующий )
с линейкой и транспортир.
2. Чтобы добавить два или более
векторы аналитически ,
(а)
рассчитать компонента каждого вектора,
(b) найти
суммы компонентов x и y ,
(c) использование
теорема Пифагора, чтобы найти величину равнодействующей (суммы),
(d) использование
функция арктангенса, чтобы найти угол направления
результирующий.
Пример . Найдите сумму d 1 = 3 см при 115 o , д 2 = 4 см при 38 o , d 3 = 3 см при 180 o .
три
векторы нарисованы ниже вместе с векторной суммой. Ты это видишь
в
результат R можно получить
добавив
векторы в любом порядке: d 1 + d 2 + d 3 = d 3 + d 1 + д 2 .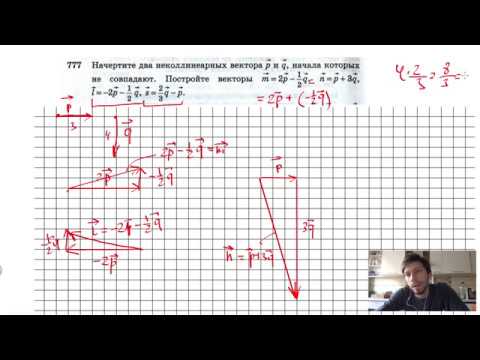 Вектор
добавление
является коммутативным.
Вектор
добавление
является коммутативным.
Аккуратное использование линейки и транспортира должен дать: R = 5,30 см на 102 o .
Сумма рассчитана . это хорошо идея нести дополнительную значащую цифру.
d 1 x = 3cos115 o =
-1,268 г 1 г = 3sin115 o = 2,719
d 2 x = 5cos38 o =
3.152 d 2 y = 5sin38 o = 2,463
d 3 x = 3cos180 o = -3 d 3 года = 3sin180 o = 0
R x 3
= S d х =
-1,116
см R г = С д г =
5,182 см
R = [(-1,116 см) 2 + (5,182 см) 2 ] 1/2 = 5,30 см
q R = тангенс -1 (5,182/-1,116) = 102 o
IV. Вычитание векторов
Вычитание векторов
S вычитание д 2 из d 1 то же, что и , добавив d 1 и — д 2 .
d 1 x = 3cos115 o знак равно
-1,268 D 1 Y = 3SIN115 O = 2,719
— D 2 x = 4COS218 O = 4COS218 O = 4COS218 O .
= — 3,152 — г 2 г = 4sin218 o = — 2,463
Ч х = —
4.420 Р у = 0,256
R = 4,43 см на 177 o
Если результирующая не находится в первом квадранте , как в этом
пример,
можно использовать следующую процедуру, чтобы найти угол результирующей
вектор.
1. Найдите арктангенс абсолютных значений из компоненты:
2. Найдите угол равнодействующей, q р ,
как указано в этой таблице.
| q Р | |||
| q Р = 180 o — q | |||
| q Р = 180 o + q | |||
| q Р = 360 o — q |
- В примере с вычитанием
выше, x -компонент отрицательный, а y -компонент
положительный.
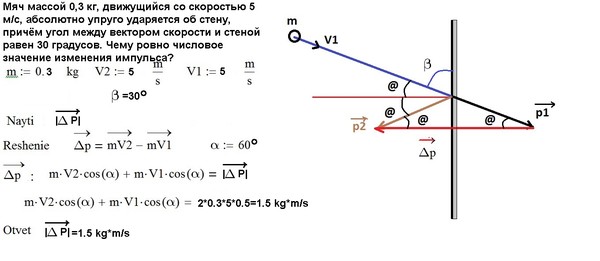 Вектор лежит во втором квадранте.
Вектор лежит во втором квадранте.ОБРАТНЫЙ TRIG-ФУНКЦИИ НА КАЛЬКУЛЯТОРЕ
Если вы настроите свой калькулятор на градусы и спросите его
найти
обратного синуса 0,5, то есть найти угол, у которого синус равен 0,5, ваш
Калькулятор должен отображать 30 или . Это,
угол, синус которого равен 0,5, равен 30 или . Теперь попросите его найти
грех(180 или –30 или ). Вы можете видеть, что sin(150 o ) также
0,5. По всей видимости,
Ваш калькулятор «умеет» вычислить синус большего угла
чем 90 или ,
но не будет возвращать значение обратного синуса больше 90 o .
Теперь посмотрим на sin -1 (-0,5). Ваш калькулятор даст вам –30 или .
В настоящее время
посмотрите на sin(210 o ) и sin(330 o ). Синусы
эти
углы также -0,5.
Похоже, ваш калькулятор всегда будет возвращать значения обратного синуса
между –90 или и 90 или для любых чисел от -1 до 1. Похожие проблемы
возникают, когда вы ищете арккосинус и арктангенс.
Похожие проблемы
возникают, когда вы ищете арккосинус и арктангенс.
Это ограничение калькулятора, который вы столкнется при работе с задачами, связанными с векторами. Вот пример. Предполагать в компоненты вектора смещения задаются как: d x = –3 и d у = –4. Если вы нарисуете эти компоненты, вы увидите, что соответствующие вектор d имеет звездную величину 5 единиц. Ты можешь также видим, что этот вектор лежит в третьем квадранте; направление угол между 180 o и 270 o . Однако, если вы запросите у калькулятора загар -1 (-4/–5)
вы увидите 53.1 o , угол в первом квадранте!
графики показаны
ниже указан рабочий диапазон (более темные участки
кривые)
калькулятор для взятия обратных триггерных функций. В таблице в предыдущем разделе показано, как
чтобы изменить угол, заданный вашим калькулятором, когда вектор в
вопрос не в первом квадранте. | |
В. Перемещение векторов в плоскости x-y.
Для удобства и пояснения схем допускается «двигаться» вектор, параллельный самому себе.
Предположим, что заданы две силы: F 1 = 3 Н в 20 o , F 2 = 5 N в 70 o .
Результирующая сила R = 7,55 Н при 55,2 o . (Вы должны быть в состоянии сделать этот расчет.)
Векторная диаграмма в этом случае более понятна, если обе
векторы
возникают в месте их применения.
Это хороший способ представления скоростей, ускорений или одновременных
сил.
Векторы соединяются хвост к хвосту, в результате получается диагональ параллелограмма, как показано здесь.
Как видите, эти два метода эквивалентны.
VI. Рабочий пример — компоненты вектора и равновесие
Кормушка для птиц весом 160 Н
поддерживается тремя кабелями, как показано здесь. Рассчитать напряжение в
каждый кабель. Рассчитать напряжение в
каждый кабель. | |
Возврат
Вектор-аддиция-слоя-прозвук-WorkSheet-Pdf-Google Suce
ALLBILDERVIDEOSBüchermapsNewshopping
Suconoptionen
Alle Anzeigen
All Anzeigen
9079Alle Anzeigen
All Anzeigen
9
. ..
ivanic1.weebly.com › загрузки › vectorworksheet4
Задачи на сложение векторов. Рабочий лист 1. Оцените с точностью до десятых. 1. а) Нарисуйте схему векторов (-3,5) и (7,1).
[PDF] Задания на векторные слова
www.npsd.k12.nj.us › Предмет › 8-2 Задания на векторные слова, примечания к классу
ВЕКТОРНОЕ СЛОВО. ПРОБЛЕМЫ. Урок 8-2. Страница 2. Общий процесс. Стр. 3. Пример 1. 7 м/с. 30 м/с. Фрисби: <30cos47, 30sin47>. = <20,46, 21,94>. Добавьте Силы:.
= <20,46, 21,94>. Добавьте Силы:.
[PDF] Задачи Vector Word
www.tamdistrict.org › cms › lib › Centricity › Domain › Vector Word…
Задачи Vector Word. Для каждой задачи нарисуйте и подпишите схему, а затем решите. Убедитесь, что все этапы четко показаны для получения полного балла.0009
[PDF] Глава 4: Добавление векторов
www.peekskillcsd.org › cms › lib › Centricity › Domain › Chap04
сумма двух или более векторов. • Решать задачи об относительной скорости. 4.1 Свойства векторов. 64. Сложение векторов. Два равных вектора. Два неравных вектора.
[PDF] HW3.2-Vector Addition Practice.pdf
www.livingston.org › cms › lib9 › Centricity › Domain › HW3.2-Vec…
Vector Addition Practice. Покажите всю свою работу на отдельных листах. Для каждой задачи нарисуйте схему ситуации и примените тригонометрию для решения …
[PDF] Таблица добавления векторов Направления
www. livingston.org › cms › lib9 › Centricity › Domain › HW3.1 Vec…
livingston.org › cms › lib9 › Centricity › Domain › HW3.1 Vec…
Таблица добавления векторов. Указания: Графически добавьте каждую пару векторов, показанных ниже, в соответствующие рамки, убедившись, что они показывают … Вектор Практика: ответы.
Задания на векторные слова с ответами Pdf — pdfFiller
www.pdffiller.com › 94795246-matchingpdf-vector…
Bewertung 4,0
(22)
Заполнить лист векторных задач с ответами Pdf, редактировать онлайн. Подписывайте, отправляйте по факсу и распечатывайте с ПК, iPad, планшета или мобильного телефона с помощью pdfFiller ✓ Мгновенно.
Марк Миракл — Средняя школа Вест Джессамин
www.jessamine.kyschools.us › папка olc ›
Глава 6 (Векторы). Примечания · Практические викторины … Ответы на лист с заданиями на самолет (лист ответов на текстовые задачи.pdf) · Практические задания на векторные задания 2 .

