Видео уроки по высшей математике: Линейная алгебра
Образовательные онлайн сервисы: теория и практика
- Главная
- Примеры
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика
- Видео-уроки
- Математический анализ
- Векторная алгебра и Аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование. Методы оптимизации
- Готовые работы
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика - Другое
- Контакты
Полезные материалы:
- Учебники
- Справочники
- Онлайн калькуляторы
- Помощь в решении
- Онлайн занятия в Zoom
Векторы
Понятие вектора 4:24
Проекция вектора 3:12
Действия над векторами 5:56
Разложение вектора по векторам (базису) 14:54
Скалярное произведение векторов 4:23
Векторное произведение векторов 5:44
Векторное произведение векторов в координатной форме 7:08
Смешанное произведение векторов 3:59
Смешанное произведение векторов в координатной форме 5:44
Определители и матрицы
Вычисление определителя 2 порядка 1:42
Определитель третьего порядка: метод треугольников и метод Саррюса 9:09
Вычисление определителя четвертого порядка 10:10
Определитель любого порядка 8:55
Умножение матриц 8:17
Миноры и алгебраические дополнение.
Урок 1. 6:04
Миноры и алгебраические дополнения. Урок 2. 12:21
Действия над матрицами 5:05
Обратная матрица 20:48
Обратная матрица. Метод алгебраических дополнений
Обратная матрица. Метод присоединенной матрицы
Системы линейных уравнений
Формулы Крамера для системы двух линейных уравнений 4:20
Метод Крамера (метод определителей) 4:20
Метод Гаусса 5:33
Метод Жордана-Гаусса (метод прямоугольников) 6:07
Метод обратной матрицы (матричный метод) 5:26
Неопределенные системы 6:19
Квадратичные формы. Кривые 2 порядка
Метод Лагранжа. Приведение квадратичной формы к каноническому и нормальному видам 6:27
Нахождение матрицы квадратичной формы в новом базисе. Матрица перехода от одного базиса к другому7:00
Задать вопрос
Заказать помощь
ОТЗЫВЫ
+7-911-7987704
vk.com/id286009794
Написать в Whatsapp
Написать в Viber
@matem96
Skype: matem96.
ru
Тест «Определители и матрицы»
«Математика – это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями»
Юджин Вигнер, американский физик и математик (1902-1995)
Часть I. Выберите один правильный ответ.
1. Раздел математики, изучающий определители и матрицы называется:
а) алгеброй
б) линейной алгеброй
в) высшей математикой
г) линейным программированием
2. Определитель – это:
а) число
б) матрица
в) таблица чисел
г) вектор
3. Чему не может быть равен определитель:
а) нулю
б) отрицательному значению
в) дробному значению
г) бесконечности
4. Порядок определителя – это:
а) диапазон значений его элементов
б) значение определителя
в) число его строк и столбцов
г) сумма индексов последнего элемента последней строки
5.
Минор определителя – это:
а) сумма элементов главной диагонали
б) произведение элементов главной диагонали
в) другой определитель, полученный из данного вычеркиванием строки и столбца
г) алгебраическое дополнение элемента определителя
6. Алгебраическое дополнение каждого элемента равно:
а) минору этого элемента, взятому с противоположным знаком
б) минору этого элемента, взятому со своим знаком
в) минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, нечетно, и с обратным знаком, если — четно
г) минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, четно, и с обратным знаком, если — нечетно
7. Разложением определителя по элементам строки называется:
а) нахождение определителя как суммы произведений элементов строки на их алгебраические дополнения
б) нахождение определителя как суммы произведений элементов столбца на их алгебраические дополнения
в) нахождение определителя как суммы произведений элементов строки на миноры этих элементов
г) нахождение определителя как суммы произведений элементов столбца на миноры этих элементов
8.
Матрица – это:
а) прямоугольная таблица чисел
б) определитель
в) отличный от нуля минор
г) неопределяемое понятие
9. Порядок может быть только у матрицы следующего вида:
а) прямоугольной
б) квадратной
в) матрицы-строки
г) любой
10. Диагональной называется матрица, у которой:
а) все элементы вне главной диагонали равны нулю
б) все элементы главной диагонали равны нулю
в) все элементы главной диагонали равны единице
г) все элементы на главной и побочной диагоналях равны нулю
11. Присоединённой матрицей к квадратной матрице может являться:
а) матрица того же порядка
б) матрица, определитель которой равен определителю данной матрицы
в) матрица порядка на один меньше, чем у данной матрицы
г) такая матрица, что произведение их определителей равно единице
12.
Чтобы вычислить произведение матрицы на число, нужно:
а) умножить элементы главной диагонали на это число
б) умножить элементы первой строки на это число
в) умножить элементы первого столбца на это число
г) умножить каждый элемент на это число
13. При умножении матрицы на единичную матрицу будет получена:
а) исходная матрица
б) транспортированная матрица
в) обратная матрица
г) единичная матрица
14. Операция умножения матриц не обладает свойством:
а) ассоциативности
б) коммутативности
в) дистрибутивности
15. Система линейных уравнений называется совместной, если она:
а) имеет единственное решение
б) не имеет решений
в) имеет бесконечное множество решений
г) имеет хотя бы одно решение
16. При решении систем уравнений методом Гаусса нельзя:
а) удалять равные или пропорциональные строки кроме одной
б) любую строку умножать или делить на некоторое число
в) переставлять местами строки
г) умножать любой столбец на некоторое число
17.
Если при решении системы уравнений методом Крамера все определители равны нулю, то:
а) система имеет единственное решение
б) система имеет ненулевые решения
в) система имеет бесконечное множество решений
г) система не имеет решений
18. Методом обратной матрицы может быть решена:
а) любая система линейных уравнений
б) система линейных уравнений, имеющая квадратную матрицу
в) система линейных уравнений, имеющая квадратную невырожденную матрицу
г) система как линейных, так и нелинейных уравнений
19. Для решения систем линейных уравнений методом Крамера в MS Excel ее главный и вспомогательные определители вычисляют с использованием функции:
а) МОБР
б) МОПРЕД
в) МУЛЬТИНОМ
г) МУМНОЖ
20. В MathCAD для нахождения определителя используют оператор Determinant на панели инструментов:
а) Calculator
б) Calculus
в) Matrix
г) Evaluation
Часть II.
Выберите несколько правильных ответов.
1. Свойства определителей:
а) определитель транспонированной матрицы равен определителю исходной матрицы
б) определитель обратной матрицы равен определителю исходной матрицы
в) умножение всех элементов строки или столбца определителя на некоторое число равносильно умножению определителя на это же число
г) если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный
д) если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю
е) если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен единице
ж) если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю
з) определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали
и) если все элементы k-ой строки (столбца) определителя представлены в виде сумм ak j + bk j, то определитель можно представить в виде произведения двух определителей
к) определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и то же число
л) определитель произведения двух квадратных матриц равен произведению определителей этих матриц
2.
К элементарным преобразованиям матриц относятся:
а) перестановка строк
б) умножение любой строки на число, отличное от нуля
в) прибавление к одной из строк любой другой строки, умноженной на любое число
г) приписывание к данной матрице единичной матрицы
д) умножение любой строки матрицы на другую строку
е) замена строк матрицы ее столбцами
3. К арифметическим действиям над матрицами относятся:
а) нахождение обратной матрицы
б) нахождение транспортированной матрицы
в) сумма матриц
г) произведение матрицы на число
д) произведение матриц
е) деление матриц
Часть III. Каждому элементу первого столбца поставьте в соответствие один или несколько элементов второго столбца.
1. Виды матриц.
Виды матриц: | Характеристики: |
1. | А. число строк матрицы совпадает с числом столбцов |
2. вырожденная | Б. матрица, составленная из алгебраических дополнений элементов данной матрицы, разделенных на величину определителя исходной матрицы |
3. квадратная | В. получена из данной матрицы заменой строк столбцами с соответствующим номером |
4. диагональная | Г. определитель матрицы равен нулю |
5. единичная | Д. не имеет обратной матрицы |
6. транспортированная | Е. |
| Ж. на главной диагонали стоят некоторые числа, а остальные элементы — нули |
| З. на главной диагонали стоят единицы, а остальные элементы — нули |
| И. является частным случаем диагональной матрицы |
| К. имеет определитель |
обратная
равна произведению исходной и обратной матриц2. Методы решения систем линейных уравнений.
Методы: | Характеристики: |
1. метод Гаусса | А. |
2. метод Крамера | Б. метод последовательного исключения неизвестных, приведение матрицы системы к ступенчатому виду |
3. матричный метод | В. неизвестные вычисляются как отношение определителей, полученных из определителя системы заменой соответствующих столбцов на столбец свободных членов, к определителю системы уравнений |
| Г. подходит для произвольной системы линейных уравнений |
| Д. подходит только для систем линейных уравнений, у которых число уравнений равно числу неизвестных |
| Е. |
матрица-столбец неизвестных вычисляется как произведении обратной матрицы на матрицу-столбец свободных членов
матрица системы должна быть невырожденной
Тест в интерактивной форме:
С выбором 1 ответа
Пазл «Классификация матриц»
дополнительных процентов | Мир математики Пасси
Источник изображения: http://wordpress.com
В Австралии насчитывается от 50 до 100 ядовитых видов пауков, но только два из них опасны для жизни человека: красноспинный и сиднейский. воронковый паук.
На основании этого можно сказать, что 3% австралийских пауков опасны для жизни человека.
Это означает, что 97% австралийских пауков не опасны для жизни.
9Цифра 7% была получена путем выполнения 100 – 3 = 97.
Это называется «дополнительными процентами» и является предметом этого короткого урока.
Дополнительные проценты
Дополнительные проценты в сумме составляют 100%, где 100% относится к общей сумме.
30% и 70% являются дополнительными процентами: (30 + 70 = 100) .
40% и 60% являются дополнительными процентами: (40 + 60 = 100) .
20% и 80% являются дополнительными процентами: (80 + 20 = 100) .
Дополнительные проценты полезны для нахождения недостающего процента, если мы знаем другой процент.
Например, если 70% людей любят шоколадное мороженое,
тогда 100 – 70 = 30% людей не любят шоколадное мороженое.
Если 60% учеников в классе — девочки,
, то мы можем вычислить, что 100 — 60 = 40% мальчиков.
Если 43% населения Индии проживает в городских районах,
, то 100 – 43 = 57% населения проживает за пределами городских районов.
Два процента всегда должны складываться в 100.
Итак, чтобы найти недостающий процент, мы делаем 100 — процент, который мы знаем.
Это может быть полезно помнить при решении вопросов по математике.
Дополнительные проценты Примеры
Источник изображения: http://mit.zenfs.com
Согласно Википедии, в Соединенных Штатах Америки проживает 4,52% населения Земли, где проживает более 307 000 000 человек.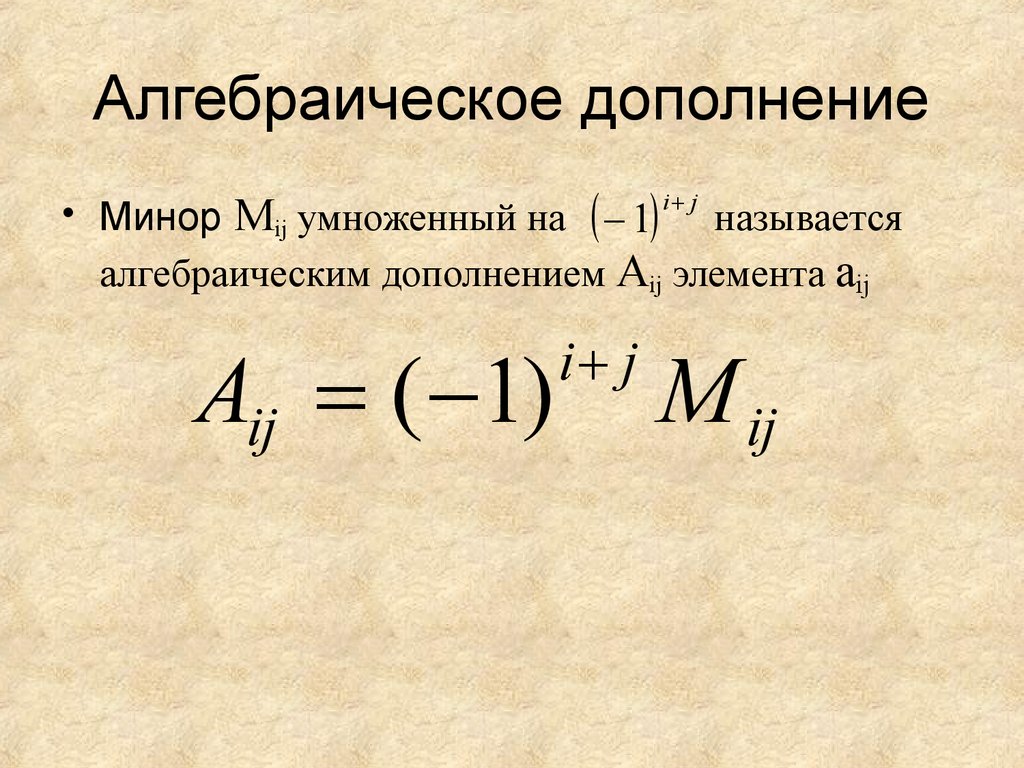
(по состоянию на 17.07.2010)
Какой процент населения мира проживает за пределами США?
Мы можем использовать дополнительные проценты, чтобы решить это, потому что люди либо живут в США, либо не живут в США.
Процент людей, не проживающих в США = 100 – 4,52 = 95,48%.
Источник изображения: http://www.howitoo.com
Если 80% из группы из 40 студентов сдали экзамен на получение водительских прав с первой попытки, то сколько студентов не сдали экзамен?
Мы знаем, что 80% успешно, поэтому 100 – 80 = 20% не прошли, потому что они не прошли.
20% от 40 = 20 разделить на 100 x 40
= 8 учащихся не сдали экзамен по вождению.
Источник изображения: http://eoimages.gsfc.nasa.gov
Идея добавления процентов к сумме 100 не ограничивается наличием двух элементов.
Воздух в земной атмосфере обычно содержит 78 % азота, 20 % кислорода, 1 % водяного пара, 0,93 % аргона и 0,04 % двуокиси углерода.
Остальное составляют другие газы.
Каков процент других газов?
Мы можем решить это, выполнив:
100 – 78 – 20 – 1 – 0,93 – 0,04
= 0,03% других газов. (Все типы)0003 Интересные проценты
Проценты и тренировки с отягощениями
Десятичные и процентные игры
Если вам понравился этот пост, почему бы не получить бесплатную подписку на наш сайт.
После этого вы сможете получать уведомления о новых страницах прямо на свой адрес электронной почты.
Перейдите в область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».
Чтобы узнать, как именно работает бесплатная подписка, нажмите на следующую ссылку:
Как работает бесплатная подписка
Если вы хотите предложить идею для статьи или стать приглашенным автором в нашем блоге, напишите нам по адресу горячей почты, указанному в правой части этой страницы.
Не стесняйтесь размещать ссылки на любые наши уроки, делиться ими в социальных сетях или использовать их в системах управления обучением в школах.
Enjoy,
Passy
Эта запись была опубликована в рубрике Без категорий и помечена Добавление процентов, дополнительные проценты, Дополнительные проценты, дополнительные проценты, итоги процентов, итоги процентов, проценты, решение процентов. Добавьте постоянную ссылку в закладки. 9\циркуляр??? угол друг к другу.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Эта идея «перпендикуляра» становится немного расплывчатой, когда мы пытаемся перенести ее в трехмерное пространство или ???n???-мерное пространство, но та же самая идея все еще существует в более высоких измерениях. Итак, чтобы уловить ту же идею, но для более высоких измерений, мы используем слово «ортогональный» вместо «перпендикулярный». Итак, два вектора (или плоскости и т.п.) могут быть ортогональны друг другу в трехмерном или ???n???-мерном пространстве. 9Ортогональное дополнение {\perp}???.
И это должно иметь для нас какой-то смысл.
В прошлом мы узнали, что два вектора ортогональны друг другу, когда их скалярное произведение равно ???0???. Например, если ???\vec{x}\cdot\vec{v}=0???, это говорит нам, что вектор ???\vec{x}??? ортогонален вектору ???\vec{v}???.
Мы хотим понять, что определение ортогонального дополнения на самом деле просто расширяет идею ортогональности с отдельных векторов на целые подпространства векторов. Таким образом, два отдельных вектора ортогональны, когда ???\vec{x}\cdot\vec{v}=0???, но два подпространства являются ортогональными дополнениями, когда каждый вектор в одном подпространстве ортогонален каждому вектору в другом подпространстве. 93\ | \ \vec{x}\cdot\begin{bmatrix}1\\ -3\\ 2\end{bmatrix}=0\ \quad\text{and}\quad\vec{x}\cdot\begin{bmatrix} 0\\ 1\\ 1\end{bmatrix}=0\}???
Если мы допустим ???\vec{x}=(x_1,x_2,x_3)???, мы получим два уравнения из этих скалярных произведений.
???x_1-3x_2+2x_3=0???
???x_2+x_3=0???
Поместите эти уравнения в расширенную матрицу,
, затем поместите его в уменьшенную форму строки-эшелона.