Математика Физика Информатика Программирование Химия Другие дисциплины Новости С Днем знаний 2017! 01/09/2017 Как всегда лето пролетело незаметно, осень наступила внезапно, и новый учебный год начался как всегда некстати. Однако с этим чередованием в «круге жизни» ничего не поделаешь, но облегчить страдания тружеников за партами в аудиториях естественно можно. С Новым 2017 годом, дорогие друзья! 30/12/2016 Дорогие друзья, как летит время! Снова пролетел еще один год, или «две сессии, две промежуточные аттестации и двое каникул». Близится Новый 2017 год! Neudoff.net — нам 7 лет! 05/11/2016 Время неумолимо несется вперед! Не успеваешь оглянуться, как пролетает не только месяц сессии, или летние каникулы, но и целый год. |
Вы нашли решение проблем! Мы вам поможем!О насАгентство Neudoff.net на протяжении многих лет работает на рынке образовательных услуг. Мы занимаемся решением задач и контрольных работ по линейной алгебре (и иным физмат дисциплинам) на заказ. У нас работают только лучшие специалисты. У каждого сотрудника нашей компании есть высшее физико-математическое образование и большой опыт работы в данной сфере. Мы поможем вам справиться с любыми проблемами, касающимися вашей учебы. Наши возможностиЛинейная алгебра довольно популярный предмет. Его изучают во всех высших учебных заведениях, в независимости от специальности. Он может проходиться как отдельная дисциплина, а может входить неявно в состав высшей математики. За время работы сервиса наши сотрудники успешно выполнили далеко не один десяток контрольных работ по линейной алгебре. Специалисты сервиса с радостью возьмут на себя часть вашей учебной нагрузки. К тому же, мы предлагаем услуги по онлайн помощи при решении задач по линейной алгебре, например на зачете. Как сделать заказ?Воспользуйтесь специальной «Формой отправки заказа» — так сделать нам заказ проще всего. С ее помощью вы отправляете нам информацию о правилах оформления, методические указания, сроки выполнения и, конечно, сами задания. Есть и другой способ. Просто свяжитесь с нами и перешлите нам задания любым удобным для вас способом. Таких способов достаточно много:
Наши гарантииNeudoff.net — серьезная организация, которая очень дорожит своей репутацией. Если вы заказываете у нас решение задач по линейной алгебре первый раз, то вы можете нас для начала проверить. Закажите решение не целой контрольной, а только нескольких задач. Ну и после получения решения можете смело заказать остаток.
Наши бонусыДрузья, наши клиенты, сделав у нас заказ всего один раз, потом неоднократно приходили к нам снова и снова. Они много раз заказывали у нас решение контрольных работ не только по линейной алгебре, но и по другим предметам. Так же многие из них советовали нас друзьям и это очень лестно для нас! Для своих постоянных клиентов мы предусмотрели ряд бонусов — скидок на заказы.
Если вам вдруг что-то стало не понятно, то не стоит тянуть — сразу напишите нам, и мы ответим на все вопросы! Способов связи достаточно! Мы всегда онлайн! |
Мы хотим, чтобы каждый клиент оставался доволен, чтобы каждый получал правильное решение точно в срок.Линейная алгебра
Активировать высокую контрастность К основному содержанию Линейная алгебра — это часть математики, касающаяся векторов, векторных пространств и линейных отображений между такими пространствами.
Система линейных уравнений
Что такое система линейных уравнений? Сколько у них решений и как их решить? В этом видео вы узнаете ответы на все эти вопросы. 9n, делать скалярные умножения и как проверить, является ли вектор линейной комбинацией других векторов.
Наборы решений линейных уравнений
В этом видео вы узнаете о решениях систем линейных уравнений. Вы узнаете, как ступенчатая форма строки матрицы связана с наборами решений.
Матричные преобразования
В этом видео вы узнаете о матричных преобразованиях. Вы узнаете, как записать функцию векторов в виде матричного преобразования.
Умножение матриц
Как перемножать матрицы? В этом видео вы узнаете, что такое линейные преобразования и что такое композиция из нескольких линейных преобразований. Это первый шаг в понимании умножения матриц.
Обратные матрицы
В этом видео вы узнаете об обратной матрице.
Вы узнаете, когда матрица обратима и как найти обратную матрицу 2×2.
Линейные подпространства
В этом видео вы узнаете о линейных подпространствах. Вы узнаете о принципе суперпозиции и увидите примеры важных линейных подпространств.
Размеры
В этом видео вы узнаете о пространствах высших измерений. Вы узнаете, как их описывать и сколько параметров для этого нужно.
Детерминанты
В этом видео вы узнаете об определителе матрицы. Вы научитесь вычислять определитель каждой квадратной матрицы.
Правило Крамера
В этом видео вы увидите, как можно использовать определители для решения системы n линейных уравнений с n переменными, если решение единственно. Этот метод называется правилом Крамера.
Внутренний продукт и ортогональность
Когда векторы ортогональны? В этом видео вы узнаете о внутреннем произведении векторов.
С помощью внутреннего продукта вы можете определить, ортогональны ли векторы. Вы также узнаете важные свойства внутренних продуктов.
Ортогональные проекции
В этом видео вы узнаете, как найти ортогональную проекцию вектора на плоскость в трехмерном пространстве.
Процесс Грама-Шмидта
Всегда ли существует ортогональный базис? И как найти такой базис для данного подпространства? Именно эти вопросы рассматриваются в этом видео. Это имеет прямое отношение к процессу Грама-Шмидта.
Задачи наименьших квадратов
Многие инженерные проблемы связаны с подгонкой данных. Вы узнаете, как использовать метод наименьших квадратов, чтобы найти наилучшее соответствие данных модели.
Собственные векторы и собственные значения
В этом видео вы узнаете, что такое собственные векторы и собственные значения матриц. Вы увидите примеры того, как можно проверить, является ли вектор собственным вектором, а скаляр — собственным значением матрицы.
Диагональные матрицы
В этом видео вы узнаете, что существует «волшебный трюк», позволяющий сделать матричные вычисления действительно простыми! Помните о диагональных матрицах, с ними легко работать. Вы узнаете, что некоторые недиагональные матрицы можно диагонализовать, чтобы упростить вычисления.
Комплексные собственные значения
В этом видео вы узнаете, как найти собственные значения и собственные векторы матрицы, даже если характеристическое уравнение не имеет действительных решений.
Системы линейных дифференциальных уравнений
В этом видео вы узнаете о дифференциальных уравнениях и о том, как линейная алгебра может помочь в решении дифференциальных уравнений.
Симметричные матрицы
Знаете ли вы, что каждая симметричная матрица ортогонально диагонализируема? В этом видео вы узнаете об этом подробнее.
Квадратичные формы
В этом видео вы узнаете о квадратичных формах. В дополнение к их интересным математическим свойствам квадратичные формы важны, потому что они возникают во многих областях применения, таких как экономика, статистика и физика.
Верные/неверные вопросы, часть I
Как ответить на вопрос Верно/Неверно? С чего начать и какие шаги следует предпринять? В этом видео вы узнаете, как это сделать с помощью метода KISS.
Верные/неверные вопросы, часть II
В этом видео вы узнаете, как найти контрпример для вопроса Верно/Неверно и как записать свой ответ на экзамене.
Содержание
|
— 2Электротехника, математика и вспомогательный персонал
Здание 36
Mekelweg 4
2628 CD DELFT
Телефон: +31 (0) 15 27 89803
Компьютерный персонал и поддержка
Здание 28
Van Mourik Brogecmanweg 6 9015 2628 2628 2628. (0)15 27 89818
МАТЕМАТИКА 2318 — Линейная алгебра
- UH Home
- NSM
- Факультет математики
- Бакалавриат
- Курсы
- math3318
- 01
***Это руководство по курсу. Студенты должны связаться с преподавателем для получения обновленной информации о текущей программе курса, учебниках и содержании курса***
*Ранее этот курс назывался МАТЕМАТИКА 2331*
Текст: Линейная алгебра и ее приложения (6-е издание) [Твердый переплет], Дэвид С. Лэй. ISBN : 9780135851258 (действительно с весны 2023 г.
) Предварительное условие : Зачисление или одновременное зачисление на курс МАТЕМАТИКА 2414.
Описание курса : Решения систем линейных уравнений, матриц, векторных пространств, линейных преобразований, подобия собственных значений и собственных векторов.
После успешного завершения этого курса студенты будут:
- Уметь решать системы линейных уравнений, используя различные методы, включая исключение Гаусса и обращение матриц.
- Уметь выполнять матричные операции, в том числе обратные и определители.
- Продемонстрировать понимание концепций векторного пространства и подпространства.
- Продемонстрировать понимание линейной независимости, размаха и базиса.
- Уметь определять собственные значения и собственные векторы и решать задачи, связанные с собственными значениями.
- Применение принципов матричной алгебры к линейным преобразованиям.
- Продемонстрировать применение внутренних продуктов и связанных с ними норм.
[ Дополнительная информация об учебной программе курса : Вводит и предоставляет модели для применения понятий векторной алгебры. Темы включают конечномерные векторные пространства и их геометрическое значение; представление и решение систем линейных уравнений с использованием нескольких методов, включая исключение Гаусса и обращение матриц; матрицы; определители; линейные преобразования; квадратичные формы; собственные значения и собственный вектор; и приложения в науке и технике.]
Программа курса:
(1) Линейные уравнения в линейной алгебре. Независимость
1.8 Введение в линейные преобразования
1.9 Матрица линейного преобразования
(2) Алгебра матриц 9n
2.9 Размер и ранг(3) Детерминанты
3.1 Введение в детерминанты
3.2 Свойства определителей, определитель и обратимость
3.3 Правило Крамера, объем и линейные преобразования
*Матрицы перестановок (не в тексте)
(4) Векторные пространства4.
1 Векторные пространства и подпространства
4.2 Нулевые пространства, пространства столбцов и линейные преобразования
4.3 Линейно независимые множества; Базы
*4.4 Coordinate Systems
4.5 The Dimension of Vector Space
4.6 Rank
*4.7 Change of Basis
*4.9 Applications to Markov Chains(5) Eigenvalues and Eigenvectors
5.1 Eigenvectors and Eigenvalues
5.2 The Characteristic Equation
5.3 Диагонализация
*5.4 Собственные векторы и линейные преобразования
*5.5 Комплексные собственные значения
*5.6-8 Приложения(6) Ортогональность и симметричные матрицы
6.1 Inner Product, Length, and Orthogonality
6.3 Orthogonality and Projections
6.4 The Gram-Schmidt Process
6.5 Least-Squares Problems(7) Symmetric Matrices and Quadratic Forms
*7.1 Diagonalization of Symmetric Matrices
*7. 2 Квадратичные формы 90 155 *7.3 Разложение по сингулярным числам 90 003*Разделы необязательны, если позволяет время
Оценка: Проконсультируйтесь с учебным планом вашего преподавателя относительно всех правил выставления оценок.
Центр Джастина Дарта младшего Проживание:
Академические корректировки/вспомогательные средства : Система Университета Хьюстона соответствует разделу 504 Закона о реабилитации 1973 г. и Закону об американцах-инвалидах 1990 г. в отношении обеспечения разумных академических корректировок/вспомогательных средств для студентов с инвалидностью. . В соответствии с разделом 504 и рекомендациями ADA Хьюстонский университет стремится предоставлять разумные академические корректировки/вспомогательные средства студентам, которые просят и требуют их. Если вы считаете, что у вас есть инвалидность, требующая академической корректировки/вспомогательной помощи, посетите веб-сайт Центра доступности для студентов Джастина Дарта-младшего по адресу https://www.
uh.edu/accessibility/ для получения дополнительной информации.Формы размещения : Пожалуйста, посетите: https://www.uh.edu/accessibility/faq/testing/. Подробная информация об этой политике и соответствующих обязанностях учащегося изложена в Политике академических корректировок/вспомогательных средств для учащихся (01.D.09) . Для получения дополнительной информации посетите страницу правил Центра доступности для студентов Justin Dart Jr. страница.
UH CAPS
Консультационные и психологические услуги (CAPS) могут помочь учащимся, которые испытывают трудности с преодолением стресса, приспосабливаются к колледжу или испытывают грусть и безнадежность. Вы можете связаться (CAPS), позвонив по телефону 713-743-5454 в рабочее и нерабочее время для обычных встреч или если вы или кто-то из ваших знакомых находится в кризисной ситуации. Для участия в программе «Поговорим» не требуется предварительной записи, которая представляет собой консультационную услугу в удобном месте и в удобное время на территории кампуса.
) 
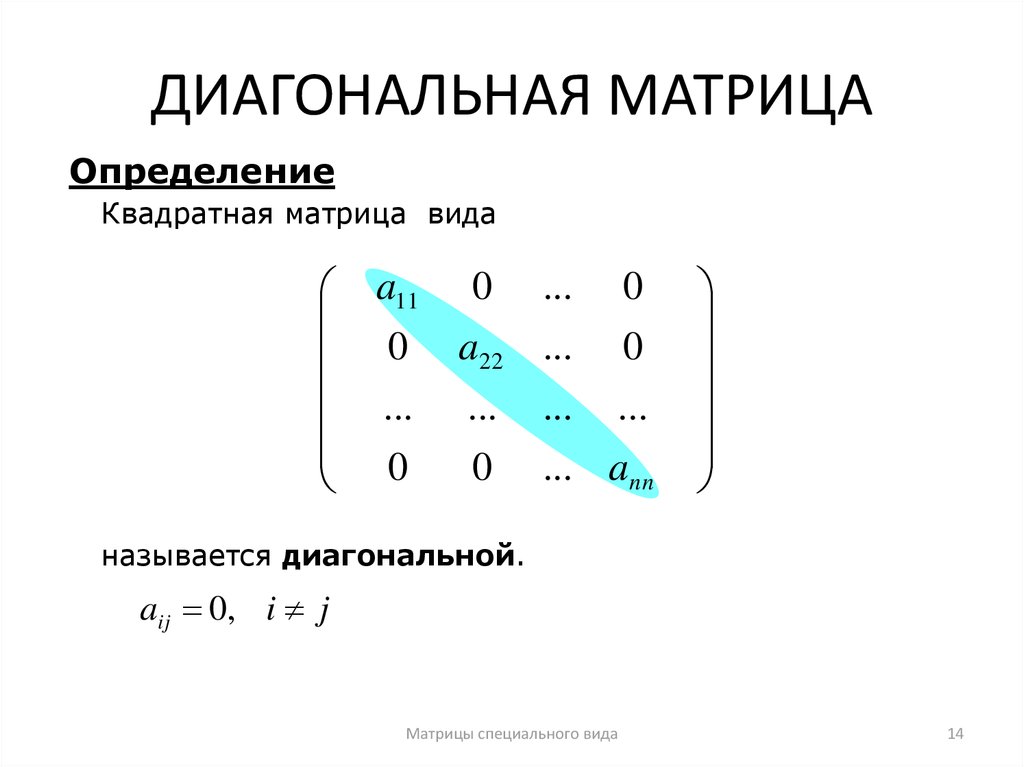1 Векторные пространства и подпространства 
2 Квадратичные формы 90 155 *7.3 Разложение по сингулярным числам 90 003
uh.edu/accessibility/ для получения дополнительной информации.