- Вертикальные асимптоты.
- Горизонтальные асимптоты.
- Наклонные асимптоты.
Вертикальные асимптоты
Уравнение любой вертикальной прямой, то есть прямой, параллельной оси OY, имеет вид x=a. Если прямая x=a является вертикальной асимптотой графика функции y=f(x), то очевидно, что хотя бы один из односторонних пределов или равен бесконечности (+∞ или -∞).Все функции с бесконечными разрывами (разрывы второго рода) имеют вертикальные асимптоты.
Пример 1. Найти уравнение вертикальных асимптот графика функции .
Решение. Видим, что y→∞, если x→1, точнее , , то есть прямая x=1 является вертикальной асимптотой, причем двусторонней.
Горизонтальные асимптоты
Всякая горизонтальная прямая имеет уравнение y=A.Если прямая y=A является горизонтальной асимптотой кривой
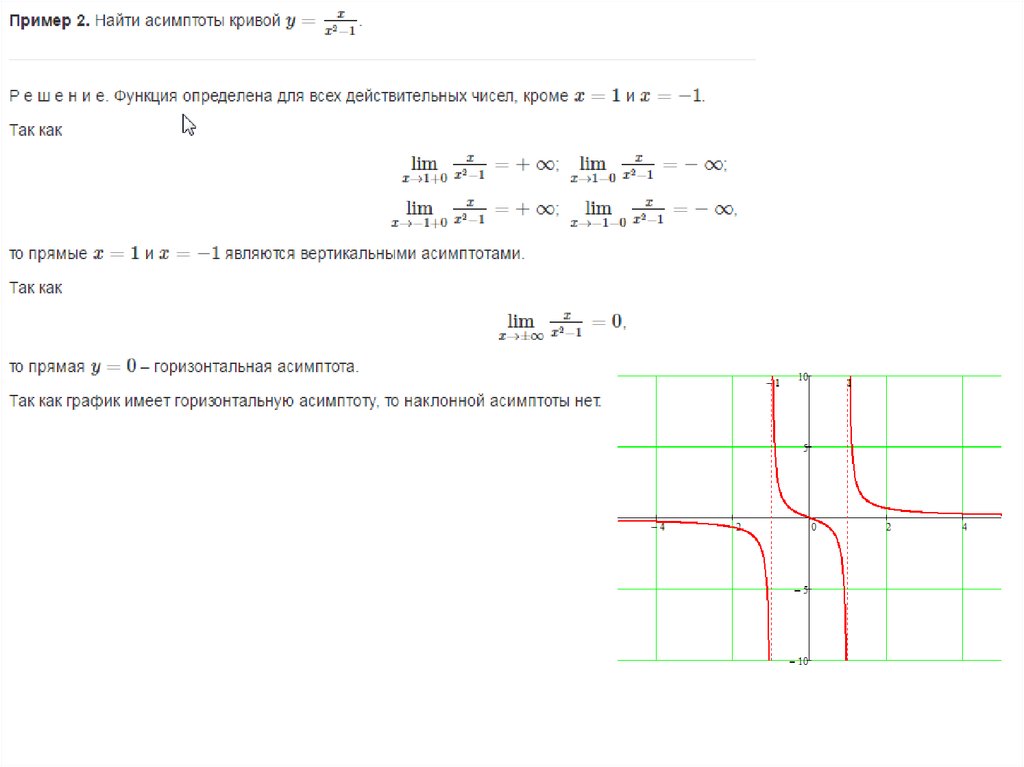
Пример 2. Найти горизонтальные асимптоты кривой .
Решение. Найдем , то есть y→0 при x→+∞ и при x→-∞, значит прямая y=0 – горизонтальная асимптота данной кривой.
Наклонные асимптоты
Уравнения наклонных асимптот обычно ищут в видеy=kx+b. По определению асимптоты или (1)
Разделим обе части этого равенства на x: , откуда
(2)
Теперь из (1):
(3)
Для существования наклонных асимптот необходимо существование пределов (2) и (3). Если хотя бы один из них не существует, то наклонных асимптот нет. Пределы (2) и (3) нужно находить отдельно при x→+∞ и при x→-∞, так как пределы могут быть разными (функция имеет две разные асимптоты).
Пример 4. Найти наклонные асимптоты графика функции .
Решение. По формуле (2) найдем .
Теперь найдем . Получаем уравнение наклонной асимптоты y=x+1.
Пример 5.
Найти асимптоты кривой y=(x-1)2(x+3).
Решение. Вертикальных и горизонтальных асимптот нет, так как y→∞ при x→∞. Ищем наклонные:
.
Таким образом, кривая асимптот не имеет.
Пример 6. Найти асимптоты кривой .
Решение. Поскольку y→∞ при x→0 и при x→4, то прямые x=0 и x=4 являются вертикальными асимптотами. Так как , то y=2 – горизонтальная асимптота. Выясним вопрос о существовании наклонных асимптот: , следовательно, кривая наклонных асимптот не имеет (искать “b” не имеет смысла, так как горизонтальные асимптоты уже найдены).
Пример 7. Построить все виды асимптот к функции
Находим коэффициент k:
Находим коэффициент b:
Получаем уравнение наклонной асимптоты:
y = -x
Найдем вертикальные асимптоты.
Для этого определим точки разрыва:
Находим переделы в точке
— является вертикальной асимптотой.
Находим переделы в точке
— является вертикальной асимптотой.
Асимптоты графика функции, формулы и примеры решения задач
Содержание:
- Виды асимптот
- Нахождение наклонной асимптоты
Виды асимптот
Определение
Прямая $x=x_{0}$ называется вертикальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $\lim _{x \rightarrow x_{0}-0} f(x)$ или $\lim _{x \rightarrow x_{0}+0} f(x)$ равно $+\infty$ или $-\infty$ .
Замечание. Прямая $x=x_{0}$ не может быть вертикальной асимптотой, если функция непрерывна в точке $x=x_{0}$ . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Определение
Прямая $y=y_{0}$ называется горизонтальной асимптотой графика функции $y=f(x)$, если
хотя бы одно из предельных значений $\lim _{x \rightarrow+\infty} f(x)$ или
$\lim _{x \rightarrow-\infty} f(x)$ равно
$y_{0}$ .
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Определение
Прямая $y=k x+b$ называется наклонной асимптотой графика функции $y=f(x)$, если $\lim _{x \rightarrow \infty}[f(x)-k x-b]=0$
Нахождение наклонной асимптоты
Теорема
(условиях существования наклонной асимптоты)
Если для функции $y=f(x)$ существуют пределы $\lim _{x \rightarrow \infty} \frac{f(x)}{x}=k$ и $\lim _{x \rightarrow \infty}[f(x)-k x]=b$, то функция имеет наклонную асимптоту $y=k x+b$ при $x \rightarrow \infty$ .
Замечание
Горизонтальная асимптота является частным случаем наклонной при $k=0$ .
Замечание
Если при нахождении горизонтальной асимптоты получается, что $\lim _{x \rightarrow \infty} f(x)=\infty$, то функция может иметь наклонную асимптоту.
Замечание
Кривая $y=f(x)$ может пересекать свою асимптоту, причем неоднократно.
{2}-x}{x+1}=\lim _{x \rightarrow \infty} \frac{-4 x+2}{x+1}=-4$
Таким образом, наклонная асимптота: $y=x-4$ .
Ответ. Вертикальная асимптота — прямая $x=-1$ .
Наклонная асимптота — прямая $y=x-4$ .
Читать дальше: исследование функции и построение ее графика.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Как найти вертикальные и горизонтальные асимптоты
Обновлено 25 октября 2018 г.
Автор: Грант Д. Маккензи
При представлении на графике некоторые функции непрерывны от отрицательной бесконечности до положительной бесконечности. Однако это не всегда так: другие функции обрываются в точке разрыва или выключаются и никогда не проходят дальше определенной точки на графике. Вертикальные и горизонтальные асимптоты — это прямые линии, определяющие значение, к которому приближается данная функция, если она не простирается до бесконечности в противоположных направлениях.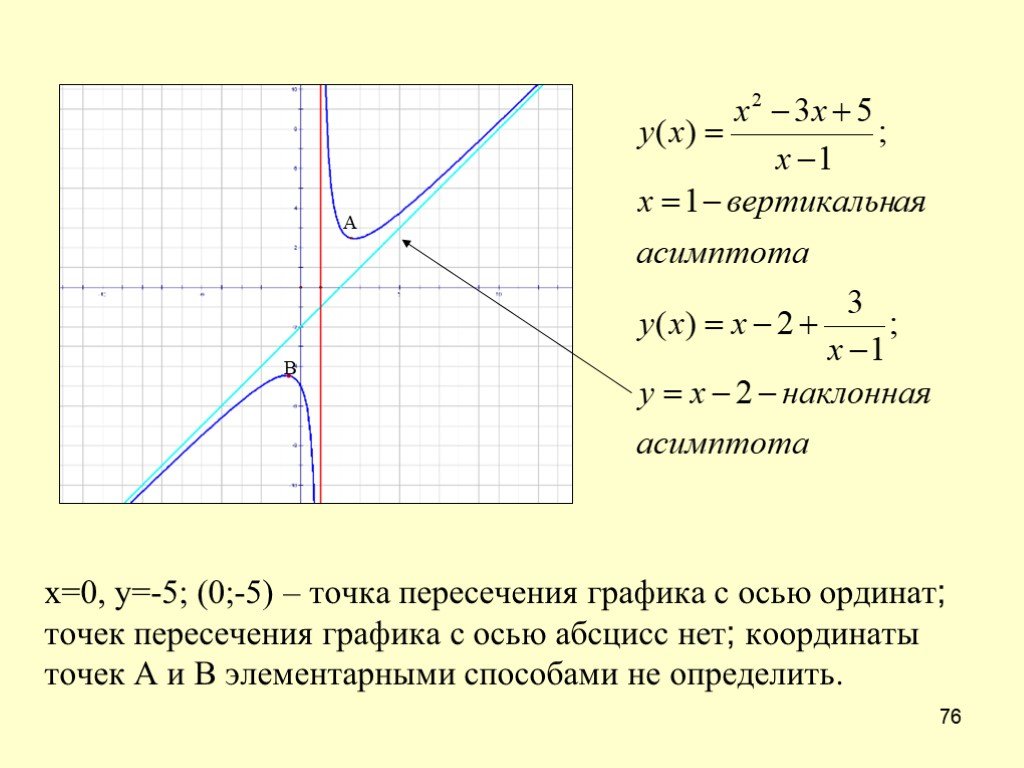
Горизонтальные асимптоты всегда следуют формуле y = C, а вертикальные асимптоты всегда следуют аналогичной формуле x = C, где значение C представляет любую константу. Нахождение асимптот, будь то горизонтальные или вертикальные, является простой задачей, если вы выполните несколько шагов.
Вертикальные асимптоты: первые шаги
Чтобы найти вертикальную асимптоту, сначала запишите функцию, для которой вы хотите определить асимптоту. Скорее всего, эта функция будет рациональной, где где-то в знаменателе стоит переменная x. Как правило, когда знаменатель рациональной функции стремится к нулю, она имеет вертикальную асимптоту. После того, как вы записали свою функцию, найдите значение x, при котором знаменатель равен нулю. Например, если функция, с которой вы работаете, равна y = 1/(x+2), вы должны решить уравнение x+2 = 0, уравнение, которое имеет ответ x = -2. Для более сложных функций может быть несколько возможных решений.
Нахождение вертикальных асимптот
Как только вы нашли значение x вашей функции, возьмите предел функции, когда x приближается к найденному значению в обоих направлениях.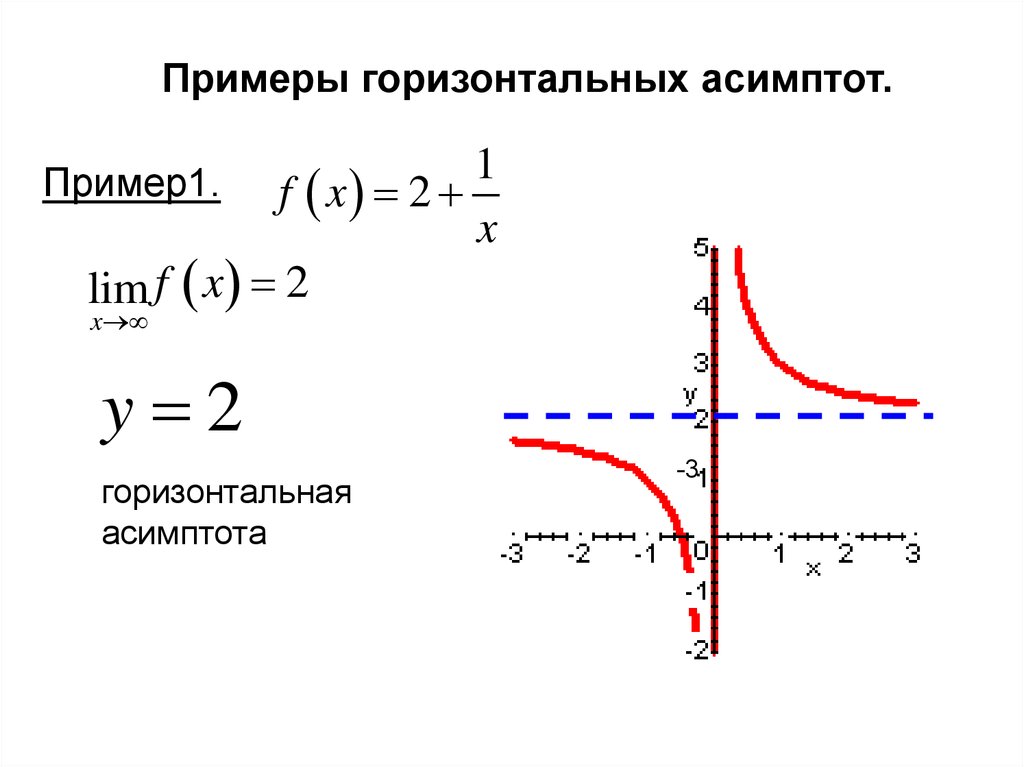
В этом примере, когда x приближается к -2 слева, y приближается к отрицательной бесконечности; когда -2 приближается справа, y приближается к положительной бесконечности. Это означает, что график функции разбивается на разрыве, перескакивая с отрицательной бесконечности на положительную бесконечность. Если вы работаете с более сложной функцией, которая имеет более одного возможного решения, вам нужно взять предел каждого возможного решения. Наконец, напишите уравнения вертикальных асимптот функции, установив x равным каждому из значений, используемых в пределах. Для этого примера имеется только одна асимптота: заданная уравнением вертикальная асимптота равна x = -2.
Горизонтальные асимптоты: первые шаги
Хотя правила горизонтальных асимптот могут немного отличаться от правил для вертикальных асимптот, процесс нахождения горизонтальных асимптот так же прост, как и поиск вертикальных. Начните с написания вашей функции. Горизонтальные асимптоты можно найти в самых разных функциях, но, скорее всего, они снова будут найдены в рациональных функциях.
В этом примере функция y = x/(x-1). Возьмите предел функции, когда x стремится к бесконечности. В этом примере «1» можно игнорировать, потому что она становится незначительной, когда x приближается к бесконечности (поскольку бесконечность минус 1 все еще остается бесконечностью). Итак, функция становится x/x, что равно 1. Следовательно, предел x/(x-1) при стремлении x к бесконечности равен 1.
Нахождение горизонтальных асимптот
Используйте решение предела, чтобы написать уравнение асимптоты. Если решение является фиксированным значением, существует горизонтальная асимптота, но если решение равно бесконечности, горизонтальной асимптоты нет. Если решением является другая функция, то асимптота есть, но она не горизонтальна и не вертикальна. Для этого примера горизонтальная асимптота равна y = 1.
Нахождение асимптот для тригонометрических функций
При решении задач с тригонометрическими функциями, у которых есть асимптоты, не беспокойтесь: найти асимптоты для этих функций так же просто, как выполнить те же шаги.
вы используете для нахождения горизонтальных и вертикальных асимптот рациональных функций, используя различные пределы. Однако при попытке сделать это важно понимать, что тригонометрические функции цикличны и, как следствие, могут иметь множество асимптот.
Нахождение горизонтальных асимптот — Бесплатная помощь по математике
Что такое горизонтальная асимптота?
Горизонтальная асимптота — это значение y на графике, к которому функция приближается, но на самом деле не достигает. Вот простой графический пример, где графическая функция приближается, но никогда не достигает \(y=0\). На самом деле, как бы вы ни уменьшали масштаб этого графика, он все равно не достигнет нуля. Однако я должен указать, что горизонтальные асимптоты могут появляться только в одном направлении и могут пересекаться при малых значениях x. Они будут отображаться для больших значений и показывать тенденцию функции по мере того, как x приближается к положительной или отрицательной бесконечности.
1) Представьте уравнение или функцию в форме y=.
2) Умножьте (расширьте) любые факторизованные многочлены в числителе или знаменателе.
3) Удалите все, кроме слагаемых с наибольшими показателями степени x в числителе и знаменателе. Это «доминирующие» термины.
Пример А: 93-9} $$
Помните, что горизонтальные асимптоты появляются, когда x простирается до положительной или отрицательной бесконечности, поэтому нам нужно выяснить, к чему приближается эта дробь, когда x становится огромным. Для этого мы выберем «доминирующие» члены в числителе и знаменателе. Доминирующими терминами являются те, у которых самые большие показатели степени. Поскольку x стремится к бесконечности, другие члены слишком малы, чтобы иметь большое значение.
Наибольшие показатели степени в этом случае совпадают в числителе и знаменателе (3).
3\) сверху и снизу. Помните, что здесь мы не решаем уравнение — мы изменяем значение, произвольно удаляя члены, но идея состоит в том, чтобы увидеть пределы функции, когда x становится очень большим. 93} $$
В данном случае 2/3 является горизонтальной асимптотой приведенной выше функции. На самом деле вы должны выразить это как \(y=\frac{2}{3}\). Это значение является асимптотой, потому что когда мы приближаемся к \(x=\infty\), «доминирующие» члены затмевают остальные, и функция всегда будет все ближе и ближе к \(y=\frac{2}{3}\ ). Вот график этой функции в качестве последней иллюстрации того, что это правильно:
(Обратите внимание, что в этой функции также присутствует вертикальная асимптота.)
Если 9Если показатель степени 0057 в знаменателе функции больше, чем показатель степени в числителе, то горизонтальная асимптота будет равна y=0, что является осью x. Когда x приближается к положительной или отрицательной бесконечности, этот знаменатель будет намного, намного больше числителя (фактически бесконечно больше), и общая дробь будет равна нулю.
Если в числителе данной функции показатель степени на больше, то НЕТ горизонтальной асимптоты. Например:
92-4} $$Горизонтальной асимптоты НЕ БУДЕТ, потому что в числителе есть БОЛЬШАЯ экспонента, равная 3. Видите? Это заставит функцию увеличиваться навсегда, а не приближаться к асимптоте. График этой функции ниже. Обратите внимание, что на графике снова присутствуют вертикальные асимптоты.
Образец B:
Найдите горизонтальные асимптоты: \(\frac{(2x-1)(x+3)}{x(x-2)}\)
В этом примере функция факторизуется форма. Однако мы должны преобразовать функцию в стандартную форму, как указано в приведенных выше шагах перед образцом A. Это означает, что мы должны умножить ее, чтобы мы могли наблюдать доминирующие члены. 92\) в числителе и знаменателе, и у нас осталось 2. Наша горизонтальная асимптота для образца B — это горизонтальная линия \(y=2\).
Ссылки на аналогичные уроки с других сайтов:
Горизонтальные асимптоты (Purplemath.