Нахождение длины отрезка по координатам: Размещение рекламы на Studygide.ru

Содержание

Расчет длины отрезка по координатам. Нахождение координат середины отрезка: примеры, решения

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Yandex.RTB R-A-339285-1 Определение 1

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Определение 2

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины).

Длину отрезка A B обозначим следующим образом: A B .

Определение 3

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .

Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C — x A = x B — x C

Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)

Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки.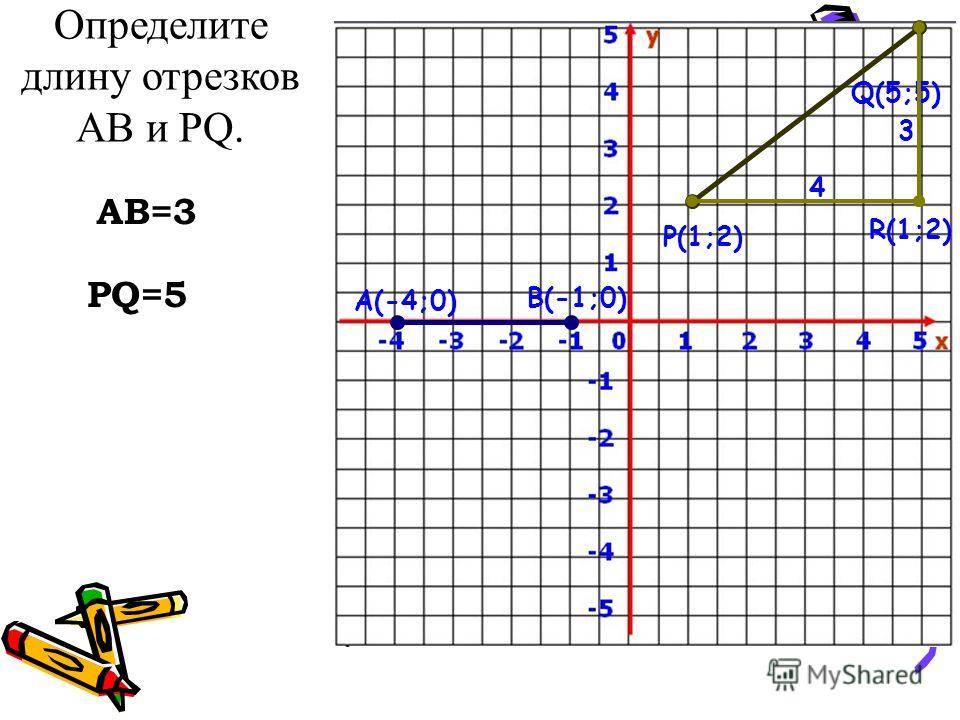

Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).

Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y .

И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :

(x A + x B 2 , y A + y B 2)

Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.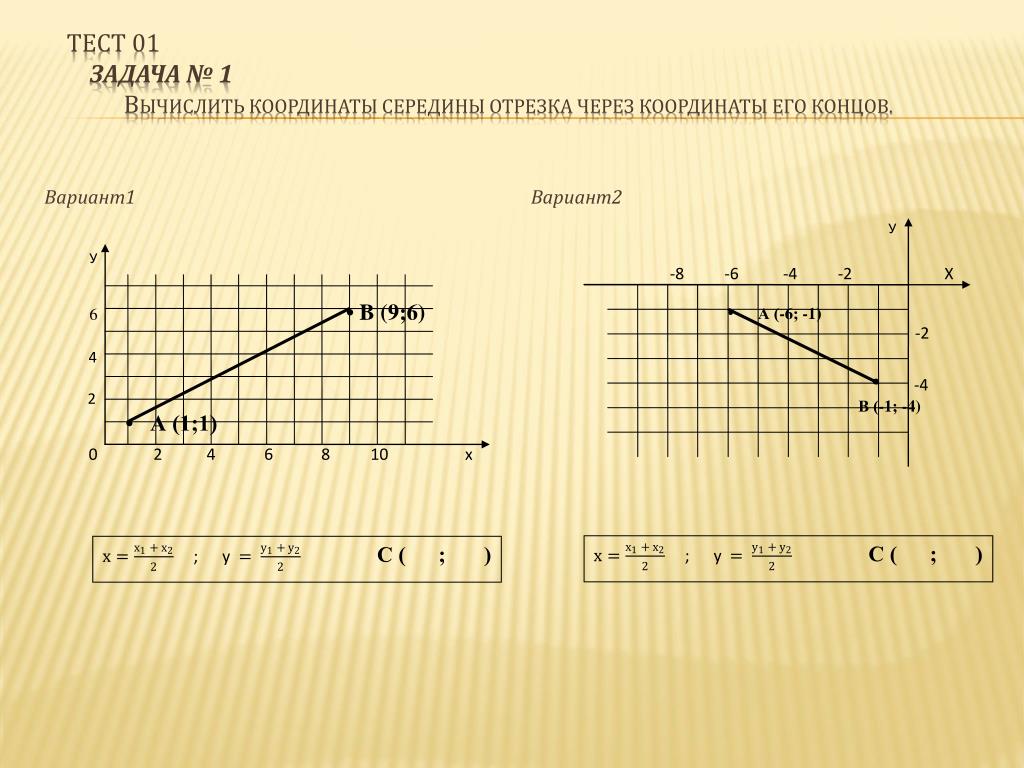 е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C (x A + x B 2 , y A + y B 2 , z A + z B 2)

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы.

Рассмотрим характерные примеры.

Пример 1

Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ : координаты середины отрезка А В — 5 2 , 7 2 .

Пример 2

Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.

Решение

По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3

Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:

A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58

Ответ: 58

Пример 3

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 .

Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8

Ответ: координаты точки А (7 , 3 , — 8) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью.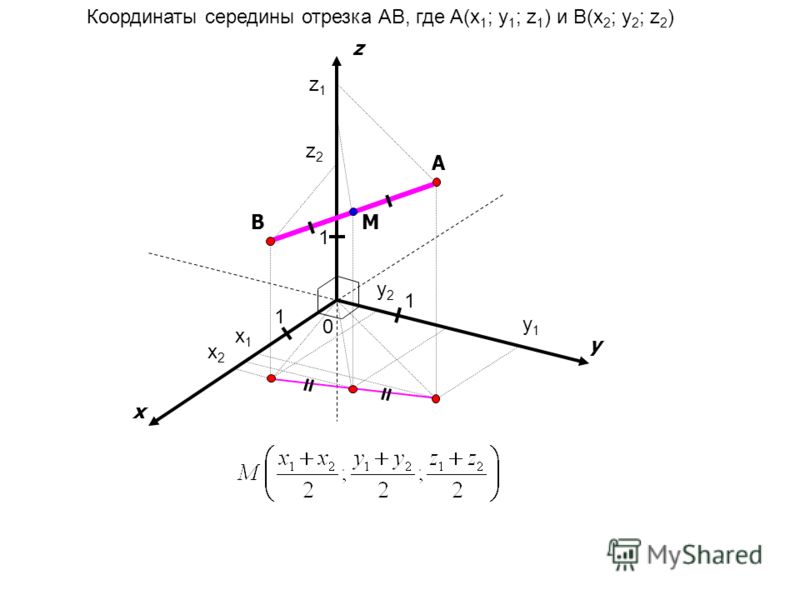

Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).

Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой. Большинству эти задания будут не интересны. Но изложить их считаю необходимым.

Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н емного теории.

Построим на координатной плоскости точку А с координатами х= 6, y=3.

Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.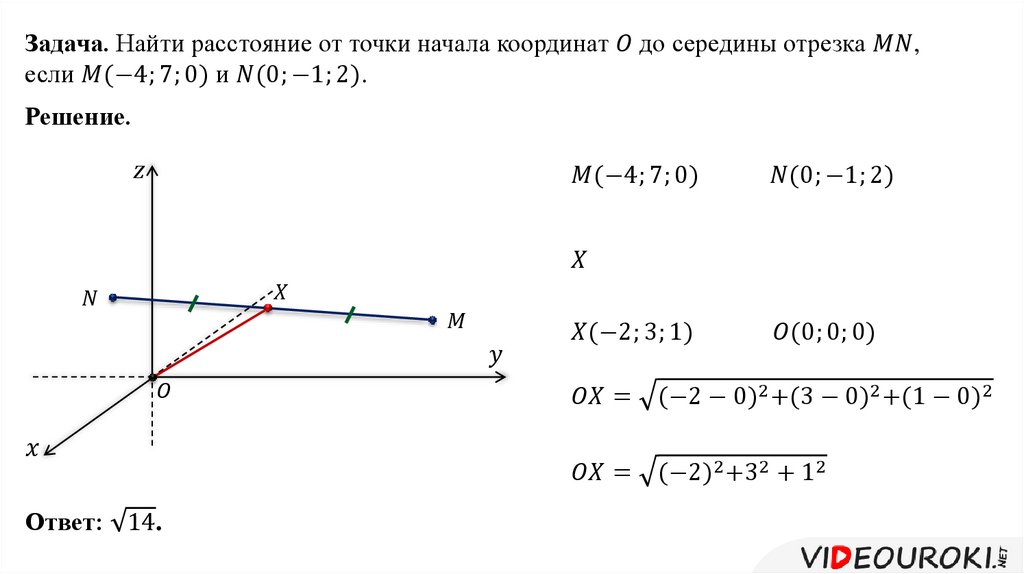

Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.

То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.

Длина отрезка на координатной плоскости

Формула для определения длины отрезка, если известны координаты его концов:

Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными

Х В – Х А и У В – У А

* * *

Середина отрезка. Её Координаты.

Формула для нахождения координат середины отрезка:

Уравнение прямой проходящей через две данные точки

Формула уравнения прямой походящей через две данные точки имеет вид:

где (х 1 ;у 1 ) и (х 2 ;у 2 ) координаты заданных точек.

Подставив значения координат в формулу, она приводится к виду:

y = kx + b , где k — это угловой коэффициент прямой

Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!

Что ещё можно добавить?

Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.

Рассмотрим задачи.

Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.

Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.

Ответ: 8

Найдите расстояние от точки A с координатами (6;8) до оси ординат.

Расстояние от точки А до оси ординат равно абсциссе точки А.

Ответ: 6.

A (6;8) относительно оси Ox .

Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).

Ордината равна минус восьми.

Ответ: – 8

Найдите ординату точки, симметричной точке A (6;8) относительно начала координат.

Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).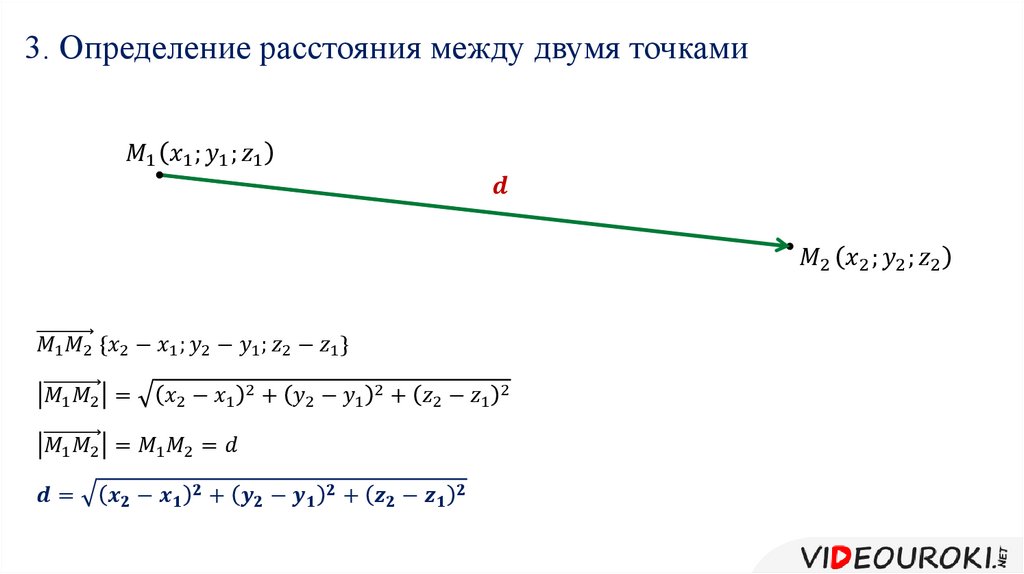

Её ордината равна – 8.

Ответ: –8

Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A (6;8).

Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).

Вычисляем по формуле:

Получили (3;4). Абсцисса равна трём.

Ответ: 3

*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.

Найдите абсциссу середины отрезка, соединяющего точки A (6;8) и B (–2;2).

Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).

Вычисляем по формуле:

Получили (2;5). Абсцисса равна двум.

Ответ: 2

*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.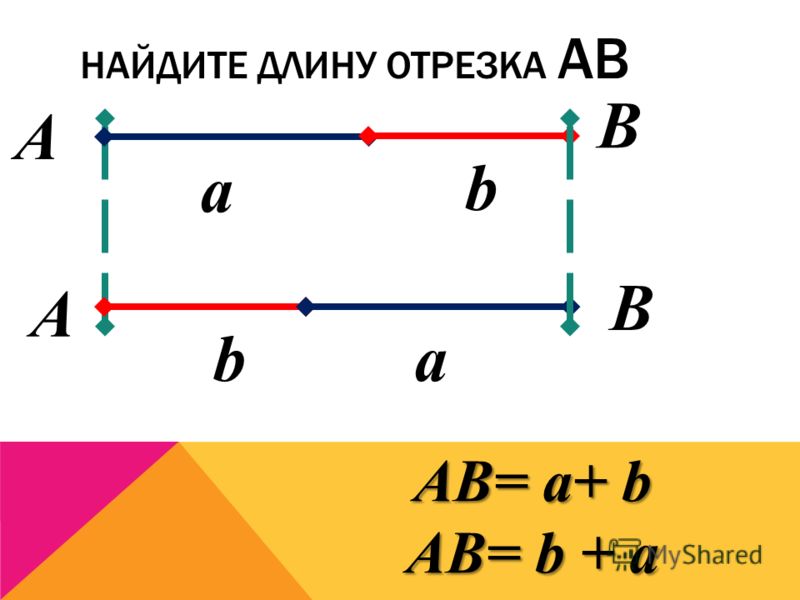

Найдите длину отрезка, соединяющего точки (0;0) и (6;8).

Длина отрезка при данных координатах его концов вычисляется по формуле:

в нашем случае имеем О(0;0) и А(6;8). Значит,

*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:

Ответ:10

Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.

Угол наклона отрезка – это угол между этим отрезком и осью оХ.

Из точки А опустим перпендикуляр на ось оХ:

То есть, угол наклона отрезка это угол ВОА в прямоугольном треугольнике АВО.

Косинусом острого угла в прямоугольном треугольнике является

отношение прилежащего катета к гипотенузе

Необходимо найти гипотенузу ОА.

По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Таким образом, косинус угла наклона равен 0,6

Ответ: 0,6

Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.

Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ .

Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.

Найдите расстояние от точки A с координатами (6;8) до начала координат.

Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.

Длина отрезка с помощью линейки

Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка.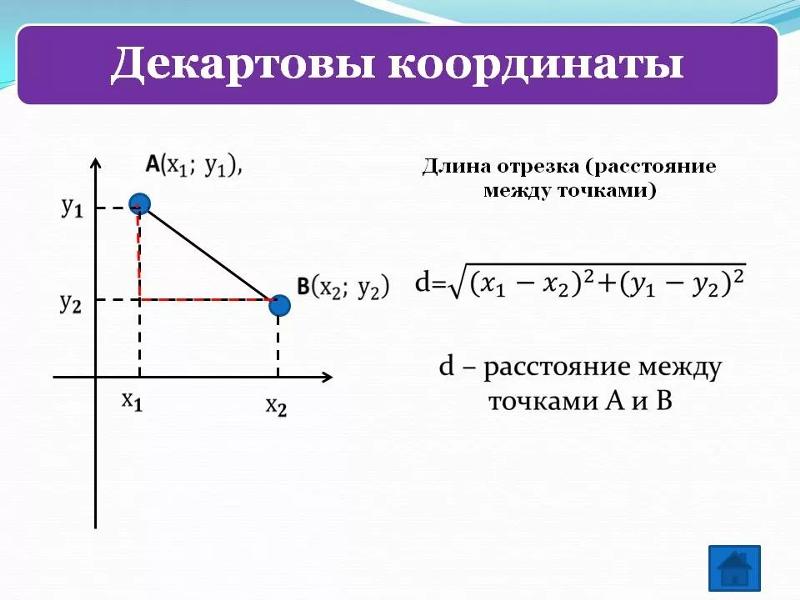 Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.

Метод координат на плоскости

Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.

Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.

Метод координат в пространстве

Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?

Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
После этого нужно возвести каждую координату вектора в квадрат.
Затем складываем квадраты координат.
Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).

Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.

Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .

Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле

Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант

Пример 3

Решение: по соответствующей формуле:

Ответ:

Для наглядности выполню чертёж

Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.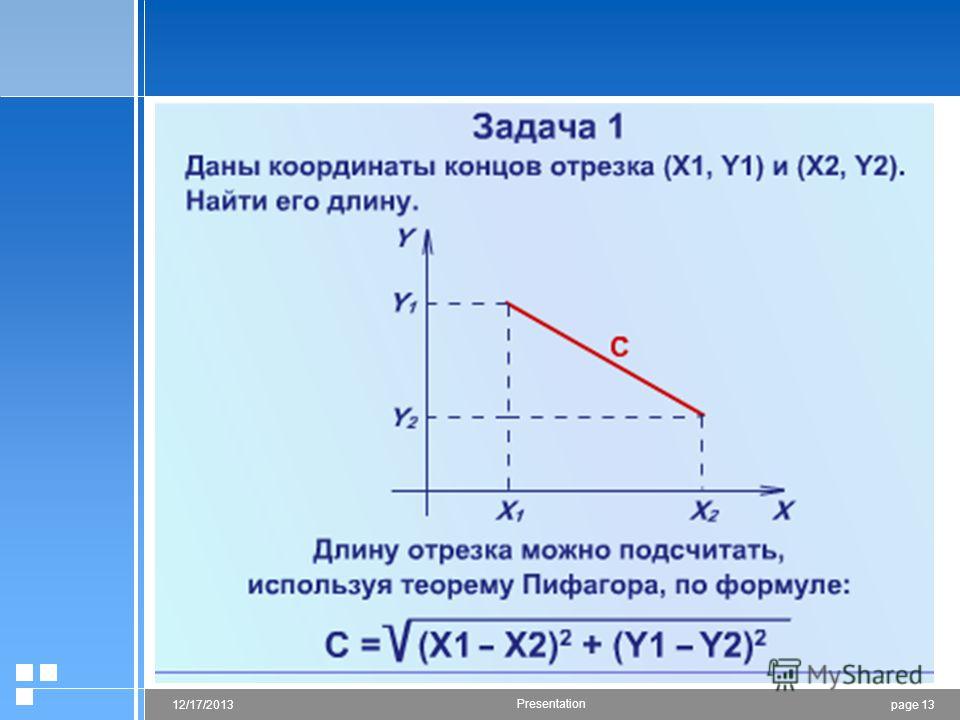

Вот другие распространенные случаи:

Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.

Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.

Давайте заодно повторим возведение корней в квадрат и другие степени:

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.

Задание для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце урока.

Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.

Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.

Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.

Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.

Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .

Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.

Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .

Рассчитаем длину отрезка А , для этого найдем квадратный корень:

A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .

Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .

Калькулятор расстояния между точками

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

Калькулятор нахождения длины отрезка поможет вычислить расстояние между заданными точками и дать подробное решение как в пространстве размерности 2d, так и в 3d.

Укажите размерность пространства 23
Задайте координаты точек
Координаты точки А: ( ; )
Координаты точки В: ( ; )

Как найти расстояние между точками плоскости и пространства

Расстояние между двумя точками в Евклидовом пространстве вычисляется по теореме Пифагора c² = a² + b² и выражается формулой:

|AB| = √(B_x — A_x)² + (B_y — A_y)² — для вычисления длины отрезка плоскости
|AB| = √(B_x — A_x)² + (B_y — A_y)² + (B_z — A_z)² — для вычисления длины отрезка пространства

Расстояние между точками в Евклидовом пространстве – называется Евклидовой метрикой, либо Евклидовым расстоянием.

Пример 1. Найдем расстояния между точками плоскости с координатами A(x; y) и точки B(x; y), где A(1; 9) и B(4; 7).
Тогда согласно формуле:

B_x = 4;
A_x = 1;
B_y = 7;
A_y = 9;

Точки A и B

Подставим значения в формулу и вычислим расстояние между точками A и B:

|AB| = √(B_x — A_x)² + (B_y — A_y)² =
√(4 — 1)² + (7 — 9)² =
√3² + (-2)² =
√9 + 4 =
√13 = 3.60555127546399

Пример 2. Найдем расстояния между точками пространства с координатами A(x; y; z) и точки B(x; y; z), где A(5; 2; 9) и B(3; 6; 7).
Тогда согласно формуле

B_x = 3;
A_x = 5;
B_y = 6;
A_y = 2;
B_z = 7;
A_z = 9;

Подставим значения в формулу и вычислим расстояние между точками A и B

|AB| = √(B_x — A_x)² + (B_y — A_y)² + (B_z — A_z)² =
√(3 — 5)² + (6 — 2)² + (7 — 9)² =
√(-2)² + 4² + (-2)² =
√4 + 16 + 4 =
√24 = 2 √6 = 4.89897948556636

Вам могут также быть полезны следующие сервисы

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка.

Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор со скобками

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление.

Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона.

Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Как найти длину отрезка когда известен.

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле

Пример 3

Решение: по соответствующей формуле:

Ответ:

Для наглядности выполню чертёж

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Вот другие распространенные случаи:

Давайте заодно повторим возведение корней в квадрат и другие степени:

Задание для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце урока.

Длина отрезка с помощью линейки

Метод координат на плоскости

Если известны координаты отрезка (х1-у1) и (х2-у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.

Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1-2) и (4-7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.

Метод координат в пространстве

Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
После этого нужно возвести каждую координату вектора в квадрат.
Затем складываем квадраты координат.
Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1-6-3) и В (3—1-7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1- -1 — 6-7 — 3) = (2—7-4).

Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3 ).

Отметим на листе бумаги две точки A и B. Эти точки можно соединить различными линиями (рис. 4 ). А как соединить точки A и B самой короткой линией? Это можно сделать с помощь линейки (рис. 5 ). Полученную линию называют отрезком .

Точка и отрезок − примеры геометрических фигур .

Точки A и B называют концами отрезка .

Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: AB или BA. Читают: «отрезок AB» или «отрезок BA».

На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.

Также принято говорить: «отрезок MN равен 3 см», «отрезок EF равен 4 см». Пишут: MN = 3 см, EF = 4 см.

Длины отрезков MN и EF мы измерили единичным отрезком , длина которого равна 1 см. Для измерения отрезков можно выбрать и другие единицы длины , например: 1 мм, 1 дм, 1 км. На рисунке 7 длина отрезка равна 17 мм. Он измерен единичным отрезком, длина которого равна 1 мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7 ).

Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается .

Длина отрезка обладает следующим свойством.

Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).

Пишут: AB = AC + CB.

На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.

Два отрезка называют равными, если они совпадут при наложении.

Следовательно отрезки AB и CD равны. Пишут: AB = CD.

Равные отрезки имеют равные длины.

Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6 отрезок EF больше отрезка MN.

Длину отрезка AB называют расстоянием между точками A и B.

Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.

Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).

Длиной ломаной называют сумму длин всех ее звеньев.

На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми .

Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.

Решение. Имеем: BC = 8 − 3 = 5 (см).

Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC = 8 + 5 = 13 (см).

Ответ: 13 см.

Пример 2 . Известно, что MK = 24 см, NP = 32 см, MP = 50 см (рис. 14 ). Найдите длину отрезка NK.

Решение. Имеем: MN = MP − NP.

Отсюда MN = 50 − 32 = 18 (см).

Имеем: NK = MK − MN.

Отсюда NK = 24 − 18 = 6 (см).

Ответ: 6 см.

Рассчитаем длину отрезка А , для этого найдем квадратный корень:

A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .

Формула длины отрезка в координатах. Нахождение координат середины отрезка, примеры, решения

Приведу подробный пример, как можно определить длину отрезка по заданным координатам с помощью онлайн-сервиса на сайте Тест Ру.

Допустим, вам нужно найти длину отрезка на плоскости

(в пространстве можно посчитать по аналогии, нужно только точку изменить на размерность три)

Отрезок AB имеет концы с координатами A (1, 2) и B (3, 4).

Для расчета длины отрезка АВ выполните следующие действия:

1. Перейдите на страницу сервиса для нахождения расстояния между двумя точками онлайн:

Мы можем использовать это, т.к. длина отрезка по координате. в точности равно расстоянию между точками A и B.

Чтобы задать правильный размер точки A, перетащите правый нижний край влево, как показано на рис.

После ввода координат первой точки А(1, 2), затем нажмите кнопку

3. На втором шаге появится форма для ввода второй точки В, введите ее координаты, как на рис. ниже:

Пункты a и b введены! Решение:

Данных очков a =

и б =

Найти расстояние между точками (точками)

отрезком называют часть прямой, состоящую из всех точек этой прямой, находящихся между данными двумя точками — их называют концами отрезка.

Рассмотрим первый пример. Пусть некоторый отрезок задан в координатной плоскости двумя точками. В этом случае мы можем найти его длину, применяя теорему Пифагора.

Итак, в системе координат нарисуйте отрезок с заданными координатами его концов (х1; у1) и (x2; y2) . на оси X и Д опускают перпендикуляры с концов отрезка. Отметьте красным отрезки, являющиеся проекциями исходного отрезка на оси координат. После этого переносим отрезки проекции параллельно концам отрезков. Получаем треугольник (прямоугольный). Гипотенуза этого треугольника будет самим отрезком АВ, а его катеты — перенесёнными проекциями.

Подсчитаем длину этих выступов. Значит по оси Y длина проекции y2-y1 , а по оси Х длина выступа x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В этом случае |AB| — длина сегмента.

Если использовать эту схему для расчета длины отрезка, то можно и отрезок не строить. Теперь посчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .

Рассмотрим следующий метод определения длины отрезка. Для этого нам нужно знать координаты двух точек в некоторой системе. Рассмотрим этот вариант с использованием двумерной декартовой системы координат.

Итак, в двумерной системе координат даны координаты крайних точек отрезка. Если провести через эти точки прямые линии, они должны быть перпендикулярны оси координат, то получится прямоугольный треугольник. Исходный отрезок будет гипотенузой получившегося треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. На основании теоремы Пифагора делаем вывод: чтобы найти длину заданного отрезка, нужно найти длины проекций на две оси координат.

Найдите длины выступов (X и Y) исходный сегмент к осям координат. Рассчитаем их, найдя разность координат точек по отдельной оси: X=X2-X1, Y=Y2-Y1 .

Рассчитать длину отрезка А , для этого находим квадратный корень:

A = √(X²+Y²) = √((X2-X1)²+(Y2-Y1)²) .

Если наш отрезок находится между точками, координаты которых 2;4 и 4;1 , то его длина соответственно равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .

В геометрии, теоретической механике и других разделах физики используются три основные системы координат: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.

Вам понадобится

Декартовы, полярные и сферические координаты концов отрезка

Инструкция

Начнем с прямоугольной декартовой системы координат. Положение точки в пространстве в этой системе координат определяется координатами x,y и z. Из начала координат в точку проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси будут равны координатам этой точки.
Предположим, теперь у вас есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. 2))

Пусть отрезок задан двумя точками на координатной плоскости, тогда его длину можно найти по теореме Пифагора.

Инструкция

Пусть заданы координаты концов отрезка (x1-y1) и (x2-y2). Нарисуйте отрезок в системе координат.

Опустите перпендикуляры от концов сегмента на оси X и Y. Отрезки, отмеченные на рисунке красным цветом, являются проекциями исходного отрезка на оси координат.

Если выполнить параллельный перенос отрезков-проекций на концы отрезков, то получится прямоугольный треугольник. Катетами этого треугольника будут переносимые проекции, а гипотенузой будет сам отрезок АВ.

Длину выступа легко рассчитать. Длина проекции на ось Y будет y2-y1, а длина проекции на ось X будет x2-x1. Тогда по теореме Пифагора |AB|²- = (y2 — y1)²- + (x2 — x1)²-, где |AB| — длина сегмента. 91/2.

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и, то длину отрезка можно вычислить по формуле

Если две точки в пространстве и задать, то длину отрезка можно вычислить по формуле

Примечание: Формулы останутся правильными, если поменять местами соответствующие координаты: и , но первый вариант более стандартный

Пример 3

Решение: по соответствующей формуле:

Ответ:

Для наглядности сделаю чертеж

Отрезок — а не 9032 это не вектор переместить его куда угодно, конечно. Кроме того, если выполнить чертеж в масштабе: 1 ед. = 1 см (две клетки тетрады), то ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.

Да, решение короткое, но в нем есть пара важных моментов, которые хотелось бы уточнить:

Во-первых, в ответе задаем размерность: «единицы». В условии не сказано ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» — сокращенно «единицы».

Во-вторых, повторим школьный материал, полезный не только для рассматриваемой проблемы:

обратите внимание на важный технический прием – вытаскивание множителя из-под корня . В результате вычислений мы получили результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Более детально процесс выглядит так: Конечно, оставление ответа в форме не будет ошибкой — но однозначно является недоработкой и весомым аргументом для придирок со стороны преподавателя.

Другие распространенные случаи:

Часто достаточно большое число получается под рутом, например. Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4:. Да, он был полностью разделен, таким образом: . А может, число снова можно разделить на 4? . Таким образом: . Последняя цифра числа нечетная, поэтому делить на 4 в третий раз явно нельзя. Пытаюсь разделить на девять: . В итоге:
Готово.

Вывод: если под корень получаем совсем не извлекаемое число, то пробуем вынести множитель из-под корня — на калькуляторе проверяем делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач часто встречаются корни, всегда старайтесь извлекать множители из-под корня во избежание более низкого балла и лишних хлопот с доработкой ваших решений по на замечание учителя.

Повторим возведение в квадрат корней и других степеней заодно:

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но я думаю, что все или почти все уже есть понятно из приведенных примеров.

Задача для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точки и . Найдите длину отрезка.

Решение и ответ в конце урока.

Измерить линию — значит найти ее длину. Длина отрезка — это расстояние между его концами.
Сегменты измеряются путем сравнения этого сегмента с другим сегментом, принятым за единицу измерения. Отрезок, принятый за единицу измерения, называется один сегмент .
Если за один отрезок принять сантиметр, то для определения длины этого отрезка нужно узнать, сколько раз сантиметр помещается в этот отрезок. В этом случае удобно измерять с помощью сантиметровой линейки.
Нарисуем отрезок AB и измерим его длину. Нанесите шкалу сантиметровой линейки на отрезок АВ так, чтобы его нулевая точка (0) совпала с точкой А :
Если окажется, что точка В совпадает с каким-то делением шкалы — например, 5, то говорят: длина отрезка АВ равна 5 см, и пишут: АВ = 5 см .
Свойства измерения линии
Когда точка делит отрезок на две части (два отрезка), длина всего отрезка равна сумме длин этих двух отрезков.
Рассмотрим сегмент AB :
Dot C делит его на два сегмента: AC и CB . Мы видим, что АС = 3 см, СВ = 4 см и АВ = 7 см. Таким образом, АС + СВ = АВ .
Любой сегмент имеет определенную длину больше нуля.
Трехмерная координатная геометрия — расстояние
Содержание
Расстояние между 2 точками
Расстояние между точкой и плоскостью
Расстояние между 2 наклонными линиями
Смотрите также
В трехмерном пространстве точки представлены их положениями вдоль осей xxx, yyy и zzz, каждая из которых перпендикулярна друг другу; это аналогично интерпретации двумерной координатной геометрии, в которой каждая точка представлена только двумя координатами (по осям xxx и yyy). 92\\&=64\\ a&=\pm2\sqrt{3}.\ _\квадрат \end{выровнено}52+a2a=82=64=±23. □
Для определения расстояния между точкой и плоскостью используется та же стратегия, что и для определения расстояния между точкой и линией. Рассмотрим плоскость, определяемую уравнением
ax+by+cz+d=0ax + by + cz + d = 0ax+by+cz+d=0
, и точку (x0,y0,z0)(x_0, y_0 , z_0)(x0,y0,z0) в пространстве. Тогда вектор нормали к плоскости равен
v=(abc)\mathbf{v} = \begin{pmatrix}a\\b\\c\end{pmatrix}v=⎝⎛abc⎠⎞
и вектор из произвольной точки на плоскости (x,y,z)(x,y,z)(x,y,z) в точку равен
w=(x0−xy0−yz0−z) .\mathbf{w} = \begin{pmatrix}x_0-x\\y_0-y\\z_0-z\end{pmatrix}.w=⎝⎛x0−xy0−yz0−z⎠⎞ .
Расстояние от точки до плоскости — это проекция w\mathbf{w}w на v\mathbf{v}v, или
D=∣projvw∣=∣v⋅w∣∣v∣=∣a (x0−x)+b(y0−y)+c(z0−z)∣a2+b2+c2=∣ax0+by0+cz0−(ax+by+cz)∣a2+b2+c2=∣ax0+ по0+cz0+d∣a2+b2+c2. \begin{выровнено} D &= |\text{proj} _{\mathbf{v}}\mathbf{w}| \\ &= \frac{|\mathbf{v} \cdot \mathbf{w}|}{|\mathbf{v}|} \\ &= \frac{|a(x_0-x)+b(y_0-y)+c(z_0-z)|}{\sqrt{a^2+b^2+c^2}} \\ &= \frac{|ax_0+by_0+cz_0-(ax+by+cz)|}{\sqrt{a^2+b^2+c^2}} \\ &= \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}. \end{выровнено} D=∣projvw∣=∣v∣∣v⋅w∣=a2+b2+c2∣a(x0−x)+b(y0−y)+c(z0−z)∣ =a2+b2+c2∣ax0+by0+cz0−(ax+by+cz)∣=a2+b2+c2∣ax0+by0+cz0+d∣.
2 3 4 5
Плоскость проходит через точку (1,−2,3)(1,-2,3)(1,−2,3) и параллельна плоскости 2x−2y+z=02x-2y+z =02x−2y+z=0. Расстояние точки (−1,2,0)(-1,2,0)(−1,2,0) от плоскости равно __________.\text{\_\_\_\_\_\_ \_\_\_\_}.__________.
Стратегия определения расстояния между двумя наклонными прямыми состоит в том, чтобы найти две параллельные плоскости, проходящие через каждую прямую; это потому, что расстояние между двумя плоскостями легко вычислить с помощью векторной проекции. Кроме того, вектор нормали к этим двум плоскостям можно вычислить с помощью перекрестного произведения векторов, представляющих направление двух линий. 9z1z2⎠⎞
, а расстояние между двумя плоскостями, равное расстоянию между двумя линиями, можно вычислить, проецируя n\mathbf{n}n на PQPQPQ, где PPP и QQQ — точки на первой и второй линиях соответственно.
Найдите расстояние между линиями
x+22=y−13=z1andx−3−1=y1=z+12.\frac{x+2}{2}=\frac{y-1}{3}=\frac{z}{1 }\quad \text{and}\quad \frac{x-3}{-1}=\frac{y}{1}=\frac{z+1}{2}.2x+2=3y−1 =1zи−1x−3=1y=2z+1.
912⎠⎞=(5−55).
Так как (−2,1,0)(-2, 1, 0)(−2,1,0) и (3,0,−1)(3, 0, -1)(3,0,−1) ) — точки на двух прямых, соответственно вектор PQPQPQ равен (5−1−1)\begin{pmatrix}5&-1&-1\end{pmatrix}(5−1−1). Затем
D=∣projnPQ∣=∣n⋅PQ∣∣n∣=2553=533. □D=\big|\text{proj}_{\mathbf{n}}PQ\big|=\frac{\big|\mathbf{n} \cdot PQ\big|}{|\mathbf{n}| }=\frac{25}{5\sqrt{3}}=\frac{5\sqrt{3}}{3}.\ _\squareD=∣∣projnPQ∣∣=∣n∣∣∣ n⋅PQ∣∣=5325=353. □
2 \sqrt{2} 2
3 \sqrt{3} 3
5 \sqrt{5} 5
6 \sqrt{6} 6

Найдите кратчайшее расстояние между следующими двумя линиями g1{g}_{1}g1 и g2:{g}_{2}:g2:
g1:x−32=y+1−2=z −2g2:x=y2=−z+4. \begin{выровнено} {g}_{1} &: \frac{x-3}{2} = \frac{y+1}{-2} = z-2 \\ {g}_{2} &: x = \frac{y}{2} = -z+4. \end{выровнено}g1g2:2x−3=−2y+1=z−2:x=2y=−z+4.
Формула расстояния
Векторы
Цитировать как: 3D-координатная геометрия — расстояние . Brilliant.org . Извлекаются из https://brilliant.org/wiki/3d-coordinate-geometry-distance/
Объяснение урока: Длина и площадь в координатной плоскости
В этом объяснении мы узнаем, как найти расстояние между двумя точками на координатной плоскости и найти площадь между тремя точками, образующими треугольник.
Концепция нахождения расстояния между точками на координатной плоскости тесно связана к теореме Пифагора. Напомним, что для треугольника с гипотенузой 𝑐 и две более короткие стороны 𝑎 и 𝑏 теорема Пифагора утверждает, что 𝑎+𝑏=𝑐.
Эта теорема означает, что если мы можем найти горизонтальное и вертикальное расстояния между две точки на координатной плоскости, то найти общее расстояние несложно.
Например, предположим, что мы рассмотрели точки (3,4) и (−2,1). Если мы нанесем их на координатную плоскость, мы увидим, что можем сформировать прямоугольный треугольник с горизонтальной стороной, вертикальная сторона и гипотенуза — отрезок, соединяющий две точки. Третья вершина находится в (3,1) как показано.
Мы можем заметить, что горизонтальное расстояние есть разница между 𝑥-координатами две точки, то есть 3−(−2)=5 единиц. Точно так же вертикальное расстояние представляет собой разницу между 𝑦-координаты, что составляет 4−1=3 единицы.
Тогда мы можем найти длину гипотенузы 𝑐, используя теорему Пифагора, 𝑎+𝑏=𝑐, где 𝑎=3 и 𝑏=5: 3+5=𝑐9+25=𝑐34=𝑐√34=𝑐.
Следовательно, гипотенуза, представляющая собой расстояние между двумя точками, может быть записана как √34 единицы.
Как и следовало ожидать, это процедура, которую можно расширить, чтобы найти расстояние между любыми общими точками на координатная плоскость. Предположим, что вместо этого у нас есть точки (𝑥,𝑦) и (𝑥,𝑦) и хочу найти расстояние между ними.
Если мы будем следовать описанной выше процедуре, мы можем создать прямоугольный треугольник, где гипотенуза является расстояние между двумя точками и две другие стороны параллельны 𝑥- и 𝑦-оси.
Как и раньше, мы можем найти длины меньших сторон, вычислив разности между двумя 𝑥-координатами и двумя 𝑦-координатами соответственно. Единственное, с чем мы должны быть осторожны, так это с тем, что эти различия могут быть отрицательными, т. поэтому мы принимаем их абсолютные значения, как показано.
Затем мы можем применить теорему Пифагора, чтобы найти гипотенузу, 𝑑, как показано: (𝑥−𝑥)+(𝑦−𝑦)=𝑑(𝑥−𝑥)+(𝑦−𝑦)=𝑑.
Обратите внимание, что при использовании этой формулы мы не нужно использовать символы абсолютного значения, потому что термины (𝑥−𝑥) и (𝑦−𝑦) возводятся в квадрат. Любое число в квадрате будет положительным; следовательно, у нас не будет проблем с «отрицательными расстояниями».
Теперь мы вывели формулу для вычисления расстояния между любыми двумя точками на координатной плоскости, которую мы можем формально определить ниже. Эту формулу часто называют в качестве формулы расстояния.
Формула: расстояние между двумя точками на координатной плоскости
Расстояние 𝑑 между двумя точками с координатами (𝑥,𝑦) и (𝑥,𝑦) определяется выражением 𝑑=(𝑥−𝑥)+(𝑦−𝑦).
Теперь мы увидим, как можно применить эту формулу в следующих примерах.
Пример 1. Использование координат двух точек для определения расстояния между ними
Найдите расстояние между 𝐿(−2,−8) и 𝑀(−6,−9), давая свой ответ в радикальной форме, если это необходимо.
Ответ
Чтобы найти расстояние между этими двумя точками, мы вспоминаем формулу расстояния, которая позволяет нам найти расстояние 𝑑 между двумя точками (𝑥,𝑦) и (𝑥,𝑦). Это расстояние определяется 𝑑=(𝑥−𝑥)+(𝑦−𝑦). 
Подстановка в (𝑥,𝑦)=(−2,−8) и (𝑥,𝑦)=(−6 ,−9), мы получаем 𝑑=(−6−(−2))+(−9−(−8))=(−4)+(−1)=√16+1=√17.единицы длины
We обратите внимание, что выбор координат, которые мы обозначаем как (𝑥,𝑦) и (𝑥,𝑦), не не важно. Например, если бы мы выбрали координаты наоборот, расчет был бы дан как 𝑑=(−2−(−6))+(−8−(−9))=√4+1=√16+1=√17.lengthunits
Это связано с тем, что каждая из разностей квадратного корня возводится в квадрат, а это означает, что результат всегда будет положительным. Это также соответствует нашей интуиции, что расстояние можно измерить с любого конца.
Давайте теперь попробуем пример, где нам дана обратная задача; то есть, зная расстояние между двумя точками, нам нужно будет найти неизвестную координату, используя формулу расстояния.
Пример 2. Нахождение неизвестной координаты по формуле расстояния
Если 𝐴(−7,𝑥) и 𝐵(9,14), где 𝐴𝐵=4√17 длина единиц, найдите все возможные значения 𝑥.
Ответ
Чтобы найти возможные значения 𝑥, мы можем использовать данную информацию о расстоянии между две точки. Напомним, что расстояние 𝑑 между двумя точками (𝑥,𝑦) и (𝑥,𝑦), определяется выражением 𝑑=(𝑥−𝑥)+(𝑦−𝑦).
Здесь нам дано, что значение 𝑑 равно 4√17, и мы можно подставить значения двух точек (𝑥,𝑦)=(9,14) и (𝑥,𝑦)=(−7,𝑥). Это дает нам 4√17=(−7−9)+(𝑥−14)=(−16)+(𝑥−14)=16+(𝑥−14).
Обратите внимание, что мы можно расширить член (𝑥−14), но на самом деле ему удобнее оставаться в факторизованной форме. В настоящее время, мы можем иметь дело с квадратными корнями, возводя в квадрат обе стороны и упрощая, что дает нам 4√17=16+(𝑥−14)16×17=16+(𝑥−14).
Затем поменяем местами стороны и перенесем постоянные члены вправо -сторона руки: (𝑥−14)=16×17−16×16=16(17−16)=16.
Мы можем решить это уравнение, еще раз извлекая квадратный корень из обеих частей. В это время, мы должны быть осторожны, чтобы учесть как положительные, так и отрицательные корни, используя ± знак. У нас есть (𝑥−14)=±√16𝑥−14=±4.
Это дает нам два возможных значения для 𝑥: 𝑥=10 и 𝑥=18. Этот означает, что есть две возможные позиции для 𝐴, отмеченные 𝐴(−7,10) и 𝐴(−7,18), которые оба лежат на линии 𝑥=−7, как показано на диаграмме ниже.
До сих пор мы исследовали только примеры с двумя точками, но их много больше приложений формулы расстояния, которые мы можем использовать. Например, если у нас есть координаты вершин фигуры (например, треугольник), то мы можем найти длины его сторон, используя формулу расстояния.
Предположим, нам дан треугольник с вершинами 𝐴(1,2), 𝐵(4,6), и 𝐶(6,1.5), как показано ниже.
Если бы нас спросили, равносторонний треугольник или нет, смогли бы мы выяснить это с помощью предоставленной нам информации? Напомним, что равносторонний треугольник — это треугольник, у которого все стороны имеют одинаковую длину. Сначала кажется, что это так, но это то, что мы должны проверить алгебраически, чтобы убедиться. В частности, если мы используем формулу расстояния для каждой пары вершин, мы можем найти длину каждой стороны и сравнить длины выяснить, действительно ли они равны.
В этот раз мы не будем демонстрировать полный расчет для каждой пары точек, но если бы мы нашли эти расстояния и отметили их на диаграмме, то обнаружили бы следующее.
То есть все стороны примерно равны 5, но они не одинаковы. Значит треугольник не равносторонний (на самом деле он разносторонний, так как ни одна из сторон не имеет одинаковой длины и ни один угол не является прямым).
Давайте рассмотрим полный пример классификации треугольника, найдя длины его сторон.
Пример 3. Классификация треугольника по длинам его сторон
Треугольник имеет вершины в точках 𝐴(4,2), 𝐵(6,2) и 𝐶(5,−1).
Определите длины сторон треугольника. Дайте свои ответы как surds в их простейшей форме.
Какой тип треугольника 𝐴𝐵𝐶?
Ответ
Часть 1
Для начала нам нужно вычислить длины сторон треугольника. Мы можем сделать это, найдя расстояние между каждой парой вершин, используя формулу расстояния. Напомним, что расстояние 𝑑 между двумя точками определяется выражением 𝑑=(𝑥−𝑥)+(𝑦−𝑦), где (𝑥,𝑦) и (𝑥,𝑦) — координаты баллы (в любом порядке).
Применим эту формулу для каждой пары точек. Для 𝐴(4,2) и 𝐵(6,2), имеем 𝐴𝐵=(6−4)+(2−2)=√2+0=2.lengthunits
Далее, для 𝐵(6,2) и 𝐶(5,−1) имеем 𝐵𝐶=(6−5)+(2−(−1))=√1+3=√10.lengthunits
Наконец, для 𝐴(4,2) и 𝐶(5,−1) , у нас есть Как видим, =√10 и 𝐴𝐶=√10 (все в единицах длины). Напомним, что треугольник с двумя равными сторонами и одной стороной другая длина — равнобедренный треугольник. Хотя это и не требуется, мы можем построить треугольник на координатной плоскости, чтобы визуализировать это.
Таким образом, длины сторон равны 𝐴𝐵=2, 𝐵𝐶=√10 и 𝐴𝐶=√10 и треугольник равнобедренный.
Когда речь идет о фигурах в координатной плоскости, нас также интересуют их площади. Чтобы найти площадь треугольника 𝐴, вспомните, что у нас есть формула 𝐴=12𝑏ℎ, где 𝑏 — длина основания, ℎ — высота. Если вопрос просит нас найти площадь треугольника, мы можем снова использовать расстояние формула, чтобы помочь нам найти количества, которые нам нужны. Единственное осложнение нам нужно быть осторожным с ориентацией треугольника, которая может изменить значения мы должны рассмотреть для основания и высоты треугольника.
Давайте рассмотрим, как это делается в следующем примере.
Пример 4. Нахождение площади треугольника, описанного линиями
Прямая 𝑙 имеет уравнение 𝑦=𝑥+6, а прямая линия 𝑙 имеет уравнение 𝑥+𝑦=30. Линии 𝑙 и 𝑙 пересекаются в точке 𝐴, а прямая 𝑙 пересекает ось 𝑥 в точка 𝐵. Вычислите площадь треугольника 𝐴𝑂𝐵, где 𝑂 — начало координат.
Ответ
Здесь нас попросили найти площадь треугольника, хотя Единственная координата, данная нам напрямую, — это вершина 𝑂, которая обозначает начало координат (0,0). Начнем с поиска двух других вершин треугольника, 𝐴 и 𝐵.
Чтобы найти 𝐴, нам нужно найти точку пересечения прямых 𝑙 и 𝑙, которую мы можем делать, решая их одновременно. Одним из способов сделать это является замена. Поскольку у нас 𝑦=𝑥+6, мы можем подставить это значение 𝑦 непосредственно в 𝑥+𝑦=30, чтобы получить 𝑥+(𝑥+6)=302𝑥+6=302𝑥=24𝑥=12.
Тогда мы можем найти 𝑦, подставив 𝑥=12 в любое уравнение. Взяв первое уравнение, 𝑦=𝑥+6, мы имеем 𝑦=12+6𝑦=18.
Итак, 𝐴=(12,18), что можно проверить, подставив во второе уравнение.
Теперь найдем 𝐵, точку пересечения 𝑙 𝑥-ось. Мы можем вычислить это, подставив 𝑦=0 в уравнение 𝑥+𝑦=30, которое немедленно дает нам 𝑥=30. Так, 𝐵=(30,0).
Теперь, когда у нас есть три точки, давайте нарисуем их на координатной плоскости так, чтобы мы можем понять, как ориентирован треугольник.
Хотя линии 𝑙 и 𝑙 также нарисованы для большей ясности, заметим, что они не обязательно должны совпадать со сторонами треугольника. Для целей этого вопроса нам нужно только рассмотреть расположение вершин треугольника.
Теперь нам нужно найти площадь треугольника, которая, как мы помним, определяется по формуле площадь=12𝑏ℎ, где 𝑏 — длина основания, а ℎ — высота треугольника. Хотя мы можем рассматривать любую из трех сторон как основание треугольника, в этом случае имеет смысл взять основание вдоль оси 𝑥, так как высота будет вертикальным расстоянием 𝐴 от оси 𝑥. Мы выделяем это ниже.
Итак, высота — это просто 𝑦-координата 𝐴(12,18), что равно 18, а длина основания равна длине 𝑂𝐵. На самом деле, поскольку 𝑂 лежит на оси 𝑦, можно сказать, что 𝑂𝐵 есть равно 𝑥-координате 𝐵(30,0), равной 30. Подставляя эти значения в формулу площади, получаем квадратные единицы площади=12×18×30=270.
В предыдущем примере у нас было преимущество работы с треугольником, где основание и высота были легко найти, до такой степени, что нам на самом деле не нужна формула расстояния. Рассмотрим несколько более сложный случай, когда нам придется вычислять эти значения явно по формуле.
Пример 5. Нахождение площади треугольника, описанного с помощью линий
Две точки 𝑅(4,−2) и 𝑆(7,0) лежат на прямой 𝑙 как показано на диаграмме.
Прямая 𝑙 перпендикулярна 𝑙, проходит через точка 𝑅 и пересекает 𝑦-ось в точке 𝑇. Вычислить площадь треугольник 𝑅𝑆𝑇 округляется до двух знаков после запятой.
Ответ
В этом примере нам дали некоторую информацию о треугольнике и его вершинах, и нам нужно найти его площадь. Напомним, что площадь треугольника 𝐴 определяется выражением 𝐴=12𝑏ℎ, где 𝑏 — длина основания, ℎ — высота. Поскольку нам дана диаграмма задачи, мы можем начать с аннотируя треугольник и количества, которые нам нужно рассчитать.
Таким образом, мы видим, что основание 𝑏 равно 𝑅𝑆, и высота, ℎ, равна 𝑅𝑇 (обратите внимание, что есть и другие стороны, которые мы могли бы выбрать в качестве базы, но это, вероятно, самый простой выбор). С тех пор, как мы даны 𝑅(4,−2) и 𝑆(7,0), мы можем найдите расстояние 𝑑 между ними, используя формулу расстояния, 𝑑=(𝑥−𝑥)+(𝑦−𝑦), где (𝑥,𝑦) и (𝑥,𝑦) — точки в вопрос. Подставляя (𝑥,𝑦)=(4,−2) и (𝑥,𝑦)=(7,0), у нас есть 𝑅𝑆=(7−4)+(0−(−2))=√3+2=√13.единицы длины
Теперь найдем 𝑅𝑇. Нам явно не дали точку 𝑇, поэтому нам нужно будет рассчитать его, используя предоставленную нам информацию. Нам сказали что он находится на линии, перпендикулярной 𝑙, поэтому мы должны начать с нахождение наклона 𝑙, что позволит нам найти уравнение 𝑙.
Поскольку у нас есть две точки 𝑅(4,−2) и 𝑆(7,0) на 𝑙, его наклон 𝑚 определяется выражением 𝑚=𝑦−𝑦𝑥−𝑥=0−(−2)7−4=23.
Далее мы вспоминаем, что перпендикулярная линия имеет наклон −1𝑚. Следовательно, 𝑙 имеет наклон −32.
Тогда мы можем найти уравнение 𝑙, используя форму точки и наклона линии, 𝑦−𝑦=𝑚(𝑥−𝑥), взяв точка (𝑥,𝑦)=𝑅(4,−2) и наклон 𝑚=−32: 𝑦−𝑦=𝑚(𝑥−𝑥)𝑦−(−2)=−32(𝑥−4)𝑦+2=−32𝑥+6𝑦=−32𝑥+4.
Теперь мы можем найти точку 𝑇 определяя, где это линия пересекает ось 𝑦. Это когда 𝑥=0, что дает нам 𝑦=4.
Наконец, мы можем найти длину 𝑅𝑇. Принимая (𝑥,𝑦)=(4,−2) и (𝑥,𝑦)=(0,4), имеем 𝑅𝑇=(0−4)+(4−(−2))=(−4)+6=√52=2√13.единицы длины
Теперь вернемся к формуле площади треугольника. Подставляя ℎ=2√13 и 𝑏=√13, мы имеют 𝐴=12√13×2√13=12×2×√13=13.squareunit
Давайте закончим обсуждением ключевых моментов, которые мы узнали в этом объяснении.
No related posts.

Расчет длины отрезка по координатам. Нахождение координат середины отрезка: примеры, решения

Определение координат середины отрезка через координаты радиус-векторов его концов

Примеры решения задач на нахождение координат середины отрезка

Длина отрезка с помощью линейки

Метод координат на плоскости

Метод координат в пространстве

Калькулятор расстояния между точками

Калькулятор нахождения длины отрезка поможет вычислить расстояние между заданными точками и дать подробное решение как в пространстве размерности 2d, так и в 3d.

Как найти расстояние между точками плоскости и пространства

Как найти длину отрезка когда известен.

Длина отрезка с помощью линейки

Метод координат на плоскости

Метод координат в пространстве

Формула длины отрезка в координатах. Нахождение координат середины отрезка, примеры, решения

Пункты a и b введены! Решение:

Вам понадобится

Инструкция

Инструкция

Свойства измерения линии

Трехмерная координатная геометрия — расстояние

Содержание

Объяснение урока: Длина и площадь в координатной плоскости

Формула: расстояние между двумя точками на координатной плоскости

Пример 1. Использование координат двух точек для определения расстояния между ними

Ответ

Пример 2. Нахождение неизвестной координаты по формуле расстояния

Ответ

Пример 3. Классификация треугольника по длинам его сторон

Ответ

Пример 4. Нахождение площади треугольника, описанного линиями

Ответ

Пример 5. Нахождение площади треугольника, описанного с помощью линий

Ответ

Добавить комментарий Отменить ответ