Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1
Решено
вычислить скалярное произведение векторов m и n, если m=a + 2b — c, n=2a — b. /a/=2. 2
2
Вариант 1.
1. Дано: вектор ā=20i+30j-60k. Найти длину вектора и направление. 2. Дано: модуль вектора равен 3, модуль вектора равен 4, угол между векторами и равен 120º. Найти модуль вектора . 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему:1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 2.
1. Дано: т.А(1, 3, 2), т.В(5, 8, 1). Найти длину вектора . 2. Определить угол между векторами ā=i+2j+3k и =6i+4j-2k. 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 3.
1. Дано: т.А(0, 0, 1), т.В(3, 2, 1), т.С(4, 5, 6), т.D(1, 6, 3). Найти координаты вектора + . 2. Найти скалярное произведение векторов ā=3i+4j+7k и =2i-5j+2k. 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 4.
1. 2. Найти скалярное произведение векторов и , если т.А(1, 0, 1), т.В(4, 2, 0), т.С(4, 0, 6), т.D(1, 2, 3). 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 5.
1. Дано: вектор ā=3i+4j-12k. Найти длину вектора ā и направление. 2. Дан треугольник с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0). Найти угол при вершине В. 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. 6. Решить систему уравнений
|
Вариант 6.
1. Найти длину вектора , если т.А(1, 2, 1), т.В(2, 2, 4), т.С(1, 2, 6), т.D(1, 3, 4). 2. Дано: вектор , вектор . Найти проекцию вектора на вектор . 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 7.
1. Дано: т.А(1, 3, 2), т.В(3, -4, 6). Найти длину и направление вектора . 2. Определить угол между векторами =2i+5j+k и =i+2j–3k. 3. 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 8.
1. Найти длины сторон треугольника с вершинами А(1, 1, 1), В(2, 3, 4), С (4, 3, 2). 2. Найти скалярное произведение векторов ā=2i+3j+5k и =i+2j+5k. 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 9.
1. 2. Дан треугольник с вершинами А(2, 1, 0), В(2, 1, 3), С(1, 1, 0). Найти угол при вершине С. 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 10.
1. Найти длину вектора 2 – , если ā=i+2j+3k, =6i+4j-2k. 2. Дано: модуль вектора равен 1, модуль вектора равен 1, угол между векторами и равен 30º. Найти скалярное произведение ( +3 , 3 + ). 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 11.
1. Найти длину вектора и направление, если А(1, 6, 1), В(3, -1, 5). 2. Дано: вектор =7i–3j+2k, вектор =3i–7j+8k. Найти проекцию вектора на вектор . 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 12.
1. Дано: вектор ā=i-2j-2k. Найти длину вектора ā и направление. 2. Дан треугольник с вершинами А(1, 2, 1), В(3, 0, 5), С (2, 0, 1). Найти угол при вершине А. 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 13.
1. Найти длину вектора + , если ā=2i–j–k, =i+j+4k. 2. Найти скалярное произведение (5 +3 , 2 – ), если модуль вектора равен 2, модуль вектора равен 3, и перпендикулярны. 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 14.
1. Найти длины сторон треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0). 2. Дано: вектор =2i–j–k, вектор =i+j+4k. Найти скалярное произведение векторов и . 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 15.
1. Найти длину вектора + , если ā=6i+3j–2k, =3i–2j+6k. 2. Дано: т.А(2, 3, -1), т.В(4, 1, -2), т.С(1, 0, 2). Найти проекцию вектора на вектор . 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 16.
1. Дано: т.А(5, 3, 7), т.В(3, 4, 1), т.С(-1, 2, 4), т.D(1, 2, 2). Найти вектор . 2. Дано: вектор =3i+4j+5k, =4i+5j–3k. Найти угол между векторами и . 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 17.
1. Найти длину вектора 2 – , если =3i+4j+5k, =4i+5j–3k. 2. Дан треугольник с вершинами А(1, 1, -1), В(2, 3, 1), С(3, 2, 1). Найти угол при вершине В. 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 18.
1. Найти длину вектора ā=2i+3j+5k и его направление. 2. Найти скалярное произведение (3 –2 , 5 –6 ), если модуль вектора равен 4, модуль вектора равен 6, угол между векторами и равен 60º. 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 19.
1. Найти длины сторон треугольника с вершинами А(0, 0, 1), В(2, 3, 5), С(6, 2, 3). 2. Найти скалярное произведение векторов ā=6i+3j–2k и =3i–2j+6k. 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 20.
1. Найти длину вектора + , если ā=6i+3j–2k, =3–2j+6k. 2. Дан треугольник с вершинами А(0, 0, 1), В(2, 3, 5), С(6, 2, 3). Найти угол при вершине В. 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 21.
1. Дано: т.А(5, 7, -2), т.В(3, 1, 1), т.С(9, 4, 4), т.Д(1, 5, 0). Найти вектор . 2. Дано: вектор =2i–j–6k, вектор =i–2j+4k. Найти проекцию вектора на вектор . 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 22.
1. Найти длину вектора ā= –i+5j–6k и его направление. 2. Дано: модуль вектора равен 5, модуль вектора равен 4, угол между векторами и равен 45º. 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 23.
1. Дано: т.А(0, 6, 2), т.В(-3, 4, 2). Найти длину вектора и направление. 2. Дано: вектор = –i+3j+4k, вектор =2i–j+2k. Найти проекцию вектора на вектор . 3. Найти произведение матриц ВА: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 24.
1. Дано: вектор =–2i+3j–2k, вектор =2i+k. Найти длину вектора . 2. Дан треугольник с вершинами А(0, 3, 1), В(2, 0, 5), С(1, 2, 3). Найти угол при вершине A. 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. методом Гаусса. 6. Решить систему уравнений
|
Вариант 25.
1. Дано: вектор =–i+j, вектор =2i+j+4k. Найти длину вектора . 2. Дано: т.А(3, 3, 1), т.В(0, 1, -2), т.С(-1, 3, 2). Найти проекцию вектора на вектор . 3. Найти произведение матриц АВ: , . 4. Вычислить определитель второго порядка . 5. Решить систему: 1. с помощью обратной матрицы; 2. по формулам Крамера; 3. 6. Решить систему уравнений
|
4.4: длина вектора
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14520
- Кен Каттлер
- Университет Бригама Янга via Lyryx
Теперь рассмотрим случай \(n=2\), показанный на следующем рисунке.
Рисунок \(\PageIndex{1}\) Есть две точки \(P =\left( p_{1},p_{2}\right)\) и \(Q = \left(q_{1},q_ {2}\справа)\) в плоскости. Расстояние между этими точками показано на рисунке сплошной линией. Обратите внимание, что эта линия является гипотенузой прямоугольного треугольника, который составляет половину прямоугольника, показанного пунктирными линиями. {1/2} \label{distance3}\] 9n\), и пусть расстояние между ними \(d( P, Q)\) задано, как в определении \(\PageIndex{1}\). Тогда выполняются следующие свойства.
{1/2} \label{distance3}\] 9n\), и пусть расстояние между ними \(d( P, Q)\) задано, как в определении \(\PageIndex{1}\). Тогда выполняются следующие свойства.
- \(d(P, Q) = d(Q, P)\)
- \(d( P, Q) \geq 0\), и равен 0 точно, когда \(P = Q.\)
Концепция расстояния имеет множество применений. Например, имея две точки, мы можем спросить, какой набор точек находится на одинаковом расстоянии между данными точками. Это исследуется в следующем примере.
9{2}-4p_3\nonumber \] Упрощая, получается \[-2p_1+14-4p_2-6p_3=-2p_2+5-4p_3\nonumber \], что можно записать как \[2p_1+2p_2+2p_3=-9 \ label{distanceplane}\] Таким образом, точки \(P = \left( p_1,p_2,p_3\right)\), находящиеся на одинаковом расстоянии от каждой из данных точек, образуют плоскость, уравнение которой задается \(\eqref {расстояние}\). Теперь мы можем использовать наше понимание расстояния между двумя точками, чтобы определить, что понимается под длиной вектора. Рассмотрим следующее определение. 92}\nonumber \]
92}\nonumber \]
Это определение соответствует определению \(\PageIndex{1}\), если вы считаете, что вектор \(\vec{u}\) имеет хвост в точке \(0 = \left ( 0, \cdots ,0 \right)\) и его кончик в точке \(U = \left(u_1, \cdots, u_n \right)\). Тогда длина \(\vec{u}\) равна расстоянию между \(0\) и \(U\), \(d(0,U)\). В общем, \(d(P,Q)=||\vec{PQ}||\).
Рассмотрим пример \(\PageIndex{1}\). По определению \(\PageIndex{2}\) мы также можем найти расстояние между \(P\) и \(Q\) как длину соединяющего их вектора. Следовательно, если бы мы нарисовали вектор \(\overrightarrow{PQ}\) с хвостом в \(P\) и точкой в \(Q\), этот вектор имел бы длину, равную \(\sqrt{47 }\). 9{н}\). Тогда вектор \(\vec{u}\), который имеет то же направление, что и \(\vec{v}\), но длина равна \(1\), является соответствующим единичным вектором вектора \(\vec{v} \). Этот вектор задается \[\vec{u} = \frac{1}{\| \vec{v} \|} \vec{v}\номер \]
Мы часто используем термин нормализовать для обозначения этого процесса. Когда мы нормализуем вектор, мы находим соответствующий единичный вектор длины \(1\). Рассмотрим следующий пример.
Когда мы нормализуем вектор, мы находим соответствующий единичный вектор длины \(1\). Рассмотрим следующий пример.
Пример \(\PageIndex{3}\): поиск единичного вектора 9T\end{aligned}\]
С помощью определения \(\PageIndex{1}\) можно проверить, что \(\| \vec{u} \| = 1\).
Эта страница под названием 4.4: Длина вектора распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- формула расстояния
- источник@https://lyryx.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра
Получение и установка длины векторов в программировании на R — функция length(): необходимо изменить заголовок
функция length() в другие объекты.
Получение длины объекта в R-программировании
Здесь мы собираемся получить длину вектора в R-программировании, для этого мы будем использовать функцию length().
Синтаксис: Длина (x)
Параметры:
- x: Vector или Object
Пример 1: Получение длины вектора
4 222222233. х <- с (6)
y <- c (1, 2, 3, 4, 5)
length (x)
length (y)
Вывод:
[1] 1 [1] 5
Пример 2: Получение длины матрицы
R
 0040 0040
|
Output:
[1] [2] [ 3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 9
Пример 3: Получение длины кадра данных
Здесь БПК представляет собой кадр данных, состоящий из 6 строк и 2 столбцов, дающих зависимость биохимической потребности в кислороде от времени при оценке качества воды.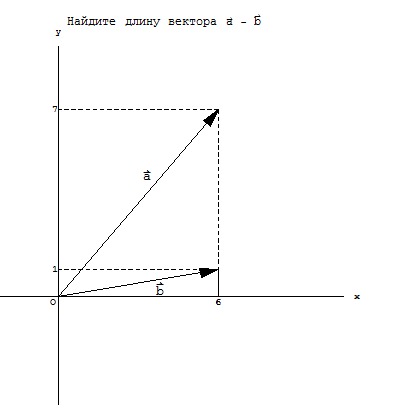 и мы собираемся получить длину этого фрейма данных.
и мы собираемся получить длину этого фрейма данных.
R
|
Output:
Time demand 1 1 8,3 2 2 10,3 3 3 19,0 4 4 16,0 5 5 15,6 6 7 19,8 2
Примечание: Если параметр является матрицей или фреймом данных, возвращается количество переменных:
Пример 4: Получение длины списка
R
|
Вывод:
[[1]] [1] 1 2 3 4 [[2]] [1] «Деби» «Сандип» «Субхам» «Шиба» [[3]] [1] 4 [1] "Длина списка:" 3
Пример 5: Получение длины строки
В языке R мы не можем легко получить длину строки, сначала мы должны получить символ строки с помощью разделения, а затем удалить каждый символ из списка, чтобы подсчитать длина.
R
|
Выход: 0
40404 15Установка длины объекта в R Programming
Здесь мы собираемся установить длину вектора в программировании на R, для этого мы будем использовать функцию length().
Syntax: length(x) <- value
Parameters:
- x: vector or object
R
9 9 9
|
Output:
[1] 3 NA [1] 1 2 3 4 5 НП НП [1] 1 2 3
Как найти длину вектора? – Reviews Wiki
Другими словами, чтобы найти длину вектора:
- квадрат горизонтальной составляющей.
- квадратный вертикальный компонент.
- сложите эти квадраты вместе.
- извлеките квадратный корень из суммы.
Какова длина вектора? Длина вектора (или величина) равна длины его стрелки и соответствует расстоянию между начальной точкой и конечной точкой . Для определения длины стрелки (и, следовательно, величины вектора) подумайте о следующем треугольнике.
Как найти длину четырехмерного вектора? Формула величины вектора может быть обобщена на произвольные измерения. Например, если a=(a1,a2,a3,a4) — четырехмерный вектор, формула для его величины будет следующей: u2225au2225=u221aa21+a22+a23+a24 .
Например, если a=(a1,a2,a3,a4) — четырехмерный вектор, формула для его величины будет следующей: u2225au2225=u221aa21+a22+a23+a24 .
Что такое векторная формула? Векторное уравнение прямой, проходящей через точку a и в направлении d: r = a + td , где t меняется.
Как найти длину вектора в линейной алгебре?
Как найти длину вектора с тремя компонентами? Ответ: Величина трехмерного вектора с 3 компонентами V = (a, b, c) определяется как √(a 2 + b 2 + c 2 ) . Давайте рассмотрим указанные шаги. Объяснение: Величина вектора означает положительную длину вектора.
Как решать векторы в математике? Чтобы работать с вектором, нам нужно уметь находить его величину и направление. Мы находим его величину, используя Теорема Пифагора или формула расстояния, и мы находим его направление с помощью функции арктангенса. Учитывая вектор положения →v=⟨a,b⟩, величина находится как |v|=√a2+b2.
Мы находим его величину, используя Теорема Пифагора или формула расстояния, и мы находим его направление с помощью функции арктангенса. Учитывая вектор положения →v=⟨a,b⟩, величина находится как |v|=√a2+b2.
Какова длина вектора (- 4 2?
Следовательно, величина вектора [4,−2] равна 2√5 .
Также Какова длина вектора (- 4 2?Поэтому модуль вектора [4,−2] равен 2√5 .
Как найти длину вектора с переменными?
Какова величина этого вектора 4 3?
Вы можете найти угол тета как тангенс – 1 (4/3) = 53 градуса. Итак, если у вас есть вектор, заданный координатами (3, 4), его величина равна 5 , а его угол равен 53 градусам.
Как найти величину отрицательного вектора?
Что имеет и величину, и направление? вектор , в физике величина, которая имеет как величину, так и направление. Обычно он изображается стрелкой, направление которой совпадает с направлением величины, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, он не имеет положения.
Какова формула a b )( ab?
В алгебраической формуле (a+ b )(a-b)= a 2 – b 2 члены по обе стороны от знака равенства называются алгебраическими выражениями
Как найти величину вектора с i и j? найти величину и направление вектора?
Для заданного вектора положения →v=⟨a,b⟩ величина находится по формуле |v|=√a2+b2.

 10.18
10.18


 Вычислить модуль вектора ā=i+2j+k и найти его направление.
Вычислить модуль вектора ā=i+2j+k и найти его направление.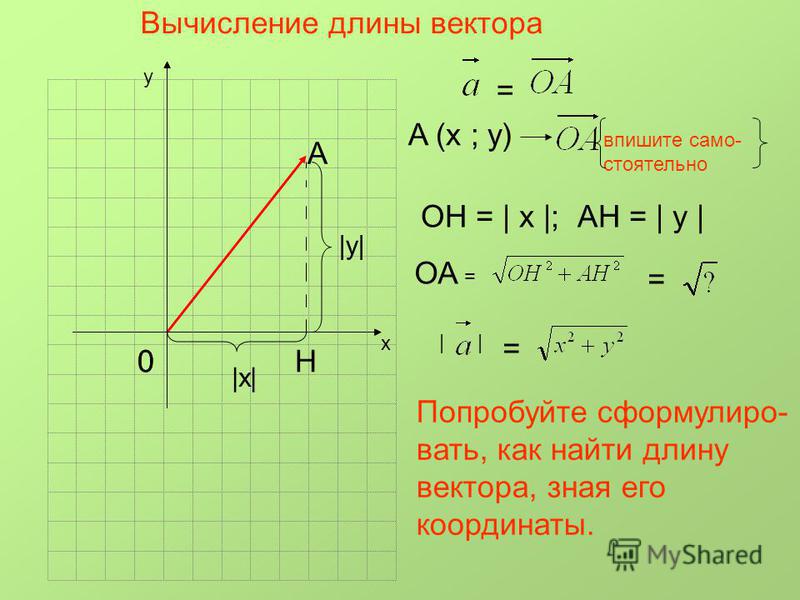 методом Гаусса.
методом Гаусса. Найти произведение матриц ВА: , .
Найти произведение матриц ВА: , .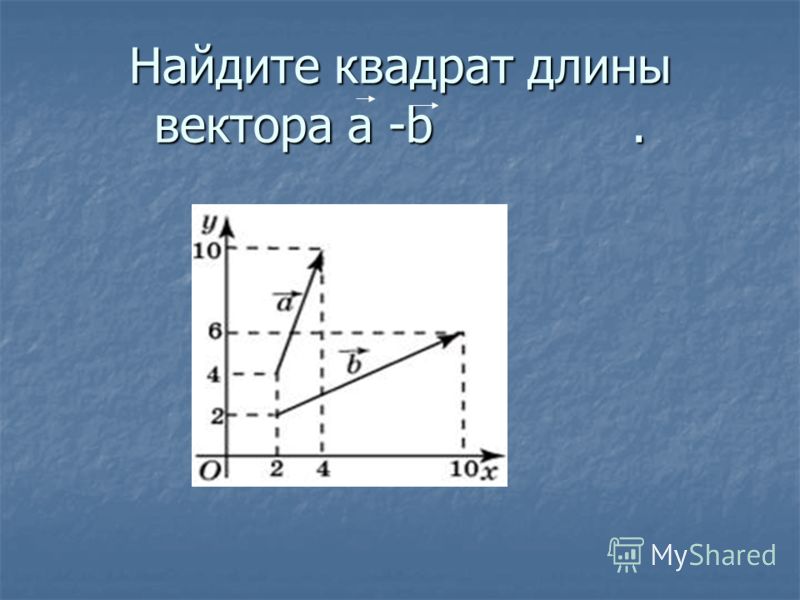
 по формулам Крамера;
по формулам Крамера;

 по формулам Крамера;
по формулам Крамера;

 по формулам Крамера;
по формулам Крамера; Найти модуль вектора =2 – .
Найти модуль вектора =2 – .
 методом Гаусса.
методом Гаусса. com/first-course-linear-алгебра
com/first-course-linear-алгебра