Простая линейная регрессия
Установка пакетов и рабочей директории
Установим необходимые для занятия пакеты (это действие необходимо, только если пакеты ещё не установлены на ваш компьютер) (для установки выполните следующую строку без символа # вначале).
# install.packages(c('foreign', 'car', 'ggplot2', 'gvlma'))Подгружаем загруженные пакеты для их использования в текущей сессии работы R.
library(foreign) library(car) library(ggplot2) library(gvlma)
Устанавливаем рабочую директорию: через меню или командой: Session -> Set working directory -> Choose directory
#setwd('...')
#(вместо '...' укажите путь к папке, в которой хранится файл)Открываем файл с данными child_data.sav. Он в формате sav (формат, используемый в SPSS), поэтому его можно открыть с помощью функции read.spss из пакета foreign.
df <- read.spss("child_data.sav", use.value.labels = T, to. data.frame = T, use.missings = T)
data.frame = T, use.missings = T)Попробуем разобраться на примере. В файле “child_data.sav” содержаться данные о школьниках (AGE — возраст, MEM_SPAN — баллы по тестированию памяти, IQ — коэффициент интеллекта, READ_AB — оценка навыков чтения).
str(df)
## 'data.frame': 20 obs. of 4 variables: ## $ AGE : num 6.7 5.9 5.5 6.2 6.4 7.3 5.7 6.15 7.5 6.9 ... ## $ MEM_SPAN: num 4.4 4 4.1 4.8 5 5.5 3.6 5 5.4 5 ... ## $ IQ : num 95 90 105 98 106 100 88 95 96 104 ... ## $ READ_AB : num 7.2 6 6 6.6 7 7.2 5.3 6.4 6.6 7.3 ... ## - attr(*, "variable.labels")= Named chr "age" "short-term memory span" "IQ" "reading ability" ## ..- attr(*, "names")= chr "AGE" "MEM_SPAN" "IQ" "READ_AB"
Посмотрим на гистограмму оценки качества чтения
hist(df$READ_AB, breaks = 10)
Видно, что по данной переменной есть разброс — одни дети читают лучше, другие — хуже. От чего это зависит? Можно предположить, что у детей с хорошей памятью лучше получается читать текст, понимать его суть и пересказывать (из этого складывается оценка по чтению). Проверим это предположение с помощью регрессионного анализа.
Построим диаграмму рассеяния для оценки качества чтения и оценки памяти.
plot <- ggplot(df, aes(READ_AB, MEM_SPAN)) + geom_point(size = 4) + theme_bw() + xlab('Чтение') + ylab('Память')
plotВизуально кажется, что качество чтения связано с качеством памяти. Проведём через эти точки прямую линию.
plot + geom_smooth(method=lm)
Проверим наличие связи с помощью регрессионного анализа методом наименьших квадратов.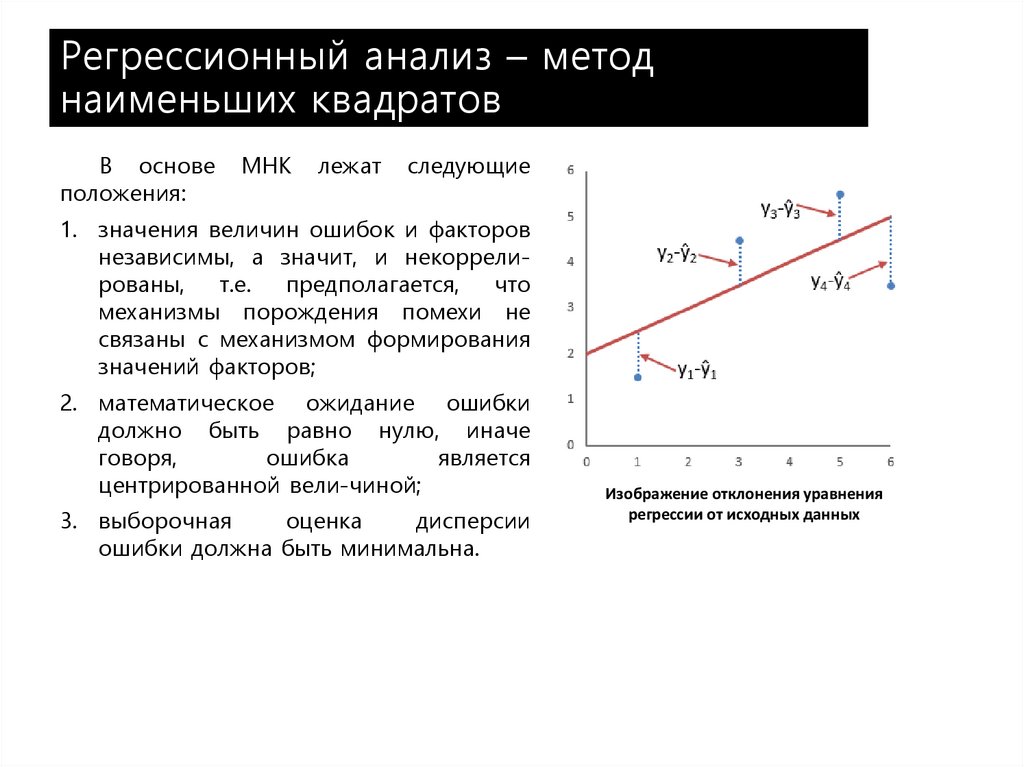
model <- lm(READ_AB ~ MEM_SPAN, data=df) summary(model)
## ## Call: ## lm(formula = READ_AB ~ MEM_SPAN, data = df) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.68955 -0.22791 -0.01045 0.21278 1.02209 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 1.8803 0.7313 2.571 0.0192 * ## MEM_SPAN 0.9767 0.1604 6.090 9.37e-06 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.4037 on 18 degrees of freedom ## Multiple R-squared: 0.6733, Adjusted R-squared: 0.6551 ## F-statistic: 37.09 on 1 and 18 DF, p-value: 9.374e-06
p-value для F-статистики для модели равняется 9.374e-06, что меньше 0.05, значит модель не является бессмысленной и объясняет какую-то часть вариации READ_AB. Чтобы понять, какую часть вариации умения читать объясняет эта модель, нужно посмотреть на значение коэффициента детерминации Multiple R-squared, которое равно 0. 6733. Т.е. наша модель объясняет 67% дисперсии умения читать.
6733. Т.е. наша модель объясняет 67% дисперсии умения читать.
Для переменной MEM_SPAN p-value меньше 0.05, следовательно мы должны отклонить нулевую гипотезу о равенстве нулю коэффициента при MEM_SPAN. Оценка этого коэффициента равна 0.9767. Запишем регрессионное уравнение полностью (уравнение для линии, которую мы провели через точки):
READ_AB = 1.8803 + 0.9767 * MEM_SPAN
Коэффициент при MEM_SPAN означает, что при увеличении оценки память на единицу ожидается увеличение умения читать на 0.9767.
Стандартную ошибку остатков (Residual standard error: 0.4037 балла) можно интерпретировать как усредненную ошибку предсказания умения читать по оценки памяти с использованием данной модели.
Посмотреть отдельно на коэффициенты
coef(model)
## (Intercept) MEM_SPAN ## 1.8803156 0.9767258
Поскольку коэффициент и константа являются оценкой, для них можно расчитать доверительный интервал.
confint(model)
## 2.5 % 97.5 % ## (Intercept) 0.3439199 3.416711 ## MEM_SPAN 0.6397881 1.313664
Посмотреть на остатки
residuals(model)
## 1 2 3 4 5 6 ## 1.02209073 0.21278107 0.11510848 0.03140039 0.23605523 -0.05230769 ## 7 8 9 10 11 12 ## -0.09652860 -0.36394477 -0.55463511 0.53605523 -0.68954635 -0.18256410 ## 13 14 15 16 17 18 ## 0.32441815 0.03605523 -0.38256410 -0.05230769 0.21278107 -0.18256410 ## 19 20 ## -0.38256410 0.21278107
Посмотреть на предсказанные значения зависимой переменной
fitted(model)
## 1 2 3 4 5 6 7 8 ## 6.177909 5.787219 5.884892 6.568600 6.763945 7.252308 5.396529 6.763945 ## 9 10 11 12 13 14 15 16 ## 7.154635 6.763945 5.689546 5.982564 6.275582 6.763945 5.982564 7.252308 ## 17 18 19 20 ## 5.787219 5.982564 5.982564 5.787219
Тестирование качества модели
Далее необходимо проверить, выполняются ли условия, лежищие в основе регрессионой МНК-модели. Наиболее распространенный подход – применить функцию plot()
par(mfrow=c(2,2)) plot(model)
Второй простой способ — общая проверка выполнения требований, предъявляемых к линейным моделям.
gvmodel <- gvlma(model) summary(gvmodel)
## ## Call: ## lm(formula = READ_AB ~ MEM_SPAN, data = df) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.68955 -0.22791 -0.01045 0.21278 1.02209 ## ## Coefficients: ## Estimate Std.Error t value Pr(>|t|) ## (Intercept) 1.8803 0.7313 2.571 0.0192 * ## MEM_SPAN 0.9767 0.1604 6.090 9.37e-06 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.4037 on 18 degrees of freedom ## Multiple R-squared: 0.6733, Adjusted R-squared: 0.6551 ## F-statistic: 37.09 on 1 and 18 DF, p-value: 9.374e-06 ## ## ## ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS ## USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM: ## Level of Significance = 0.05 ## ## Call: ## gvlma(x = model) ## ## Value p-value Decision ## Global Stat 5.8582 0.2100 Assumptions acceptable. ## Skewness 1.0395 0.3079 Assumptions acceptable. ## Kurtosis 0.3692 0.5434 Assumptions acceptable. ## Link Function 2.0686 0.1504 Assumptions acceptable. ## Heteroscedasticity 2.3808 0.1228 Assumptions acceptable.
Введение в R: часть 3
Введение в R: часть 3Pavel Polishchuk, 2014
Примеры построения моделей в R. 2 + x1*x2 + rnorm(200, 0, 0.5)
2 + x1*x2 + rnorm(200, 0, 0.5)
Объединим эти параметры в одном data.frame
df <- data.frame(y, x1, x2)
Рассмотрим созданный набор данных. Построим гистограмму распределению значений Y и посмотрим как рапределены значения переменных между собой попарно.
hist(df$y)
pairs(df)
Посчитаем матрицу взаимных корреляций всех переменных между собой и округлим результат до двух цифр после запятой
round(cor(df), 2)
y x1 x2 y 1.00 0.18 0.86 x1 0.18 1.00 -0.05 x2 0.86 -0.05 1.00
Помимо традиционного коэффицента корреляции Пирсона функцией cor можно посчитать ранговый коэффицент корреляции Спирмена.
round(cor(df, method="spearman"), 2)
y x1 x2 y 1.00 0.12 0.94 x1 0.12 1.00 -0.02 x2 0.94 -0.02 1.00
И из рисунка и из таблиц видно, что связь между \( y \) и \( x_2 \) довольно тесная.
Альтернативный способ представления данных — использование функции pairs. пакета  panels
panelspsych, которая возвращает одновременно и диаграммы распределения данных и значения коэффициентов корреляции.
psych::pairs.panels(df)
Зададим индексы для объектов обучающей и тестовой выборки
train.ids <- 1:100 test.ids <- 101:200
Построим несколько моделей в соответствии с различными формулами, которые определяют вид искомой зависимости.
Попробуем сперва обычную линейную комбинацию исходных переменных.
m1 <- lm(y ~ x1 + x2, df[train.ids,]) summary(m1)
Call:
lm(formula = y ~ x1 + x2, data = df[train.ids, ])
Residuals:
Min 1Q Median 3Q Max
-15.62 -7.56 -3.43 1.95 54.96
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.379 3.493 -1.83 0.071 .
x1 3.377 0.625 5.40 4.8e-07 ***
x2 8.567 0.415 20.65 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.
2 \]
\( y_i \) - наблюдаемое значение \( y \)
\( \hat{y}_i \) - предсказанное по модели значение \( y \)
\( \bar{y} \) - среднее значение наблюдаемых значений \( y \)
\( n \) - количество наблюдений
\( k \) - количество параметров
Применим одну из простейших процедур отбора переменных - исключим незначащие члены из уравнения
m2 <- lm(y ~ x1 + x2 + 0, df[train.ids,])
summary(m2)
Call:
lm(formula = y ~ x1 + x2 + 0, data = df[train.ids, ])
Residuals:
Min 1Q Median 3Q Max
-17.73 -8.88 -4.61 2.30 49.03
Coefficients:
Estimate Std. Error t value Pr(>|t|)
x1 2.361 0.290 8.15 1.2e-12 ***
x2 8.267 0.386 21.44 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 12.4 on 98 degrees of freedom
Multiple R-squared: 0.914, Adjusted R-squared: 0.913
F-statistic: 524 on 2 and 98 DF, p-value: <2e-16
Коэффициент детерминации существенно увеличился \( R^2 = 0. 914 \)
914 \)
Сравнение моделей
Определим с помощью дисперсионного анализа является ли отличие моделей значимым или нет.
anova(m1, m2)
Analysis of Variance Table
Model 1: y ~ x1 + x2
Model 2: y ~ x1 + x2 + 0
Res.Df RSS Df Sum of Sq F Pr(>F)
1 97 14603
2 98 15105 -1 -502 3.33 0.071 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Величина 0.071 > 0.05, поэтому можно утверждать, что с вероятностью 95% отличие моделей не значимо и мы в праве выбрать любую модель.
Попытаемся построить более сложные модели.
Модель учитывающее произведение независимых переменных
m3 <- lm(y ~ x1*x2, df[train.ids,])
summary(m3)
Call:
lm(formula = y ~ x1 * x2, data = df[train.ids, ])
Residuals:
Min 1Q Median 3Q Max
-10.35 -7.51 -3.06 3.77 51.30
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5. 132 3.623 1.42 0.160
x1 1.160 0.664 1.75 0.084 .
x2 3.866 0.890 4.34 3.5e-05 ***
x1:x2 0.962 0.167 5.77 9.5e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 10.6 on 96 degrees of freedom
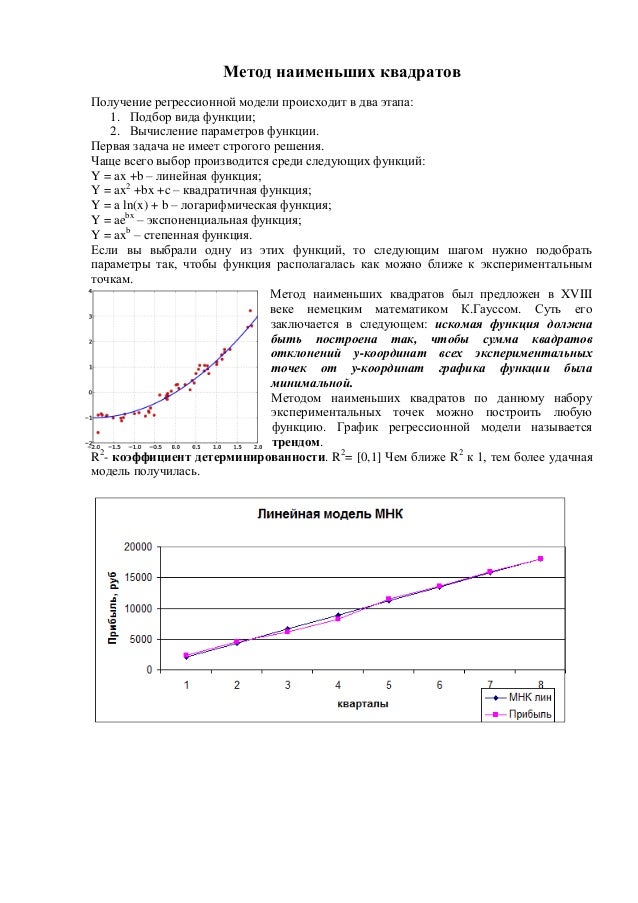
Multiple R-squared: 0.865, Adjusted R-squared: 0.861
F-statistic: 205 on 3 and 96 DF, p-value: <2e-16
132 3.623 1.42 0.160
x1 1.160 0.664 1.75 0.084 .
x2 3.866 0.890 4.34 3.5e-05 ***
x1:x2 0.962 0.167 5.77 9.5e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 10.6 on 96 degrees of freedom
Multiple R-squared: 0.865, Adjusted R-squared: 0.861
F-statistic: 205 on 3 and 96 DF, p-value: <2e-16
Модель второго порядка, учитывающая квадраты независимых переменных
m4 <- lm(y ~ poly(x1, 2) + poly(x2, 2), df[train.ids,])
summary(m4)
Call:
lm(formula = y ~ poly(x1, 2) + poly(x2, 2), data = df[train.ids,
])
Residuals:
Min 1Q Median 3Q Max
-15.569 -2.232 -0.475 1.683 22.654
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 31.056 0.594 52.27 < 2e-16 ***
poly(x1, 2)1 65.297 5.983 10.91 < 2e-16 ***
poly(x1, 2)2 -24.414 5.979 -4.08 9.3e-05 ***
poly(x2, 2)1 253. 2
2
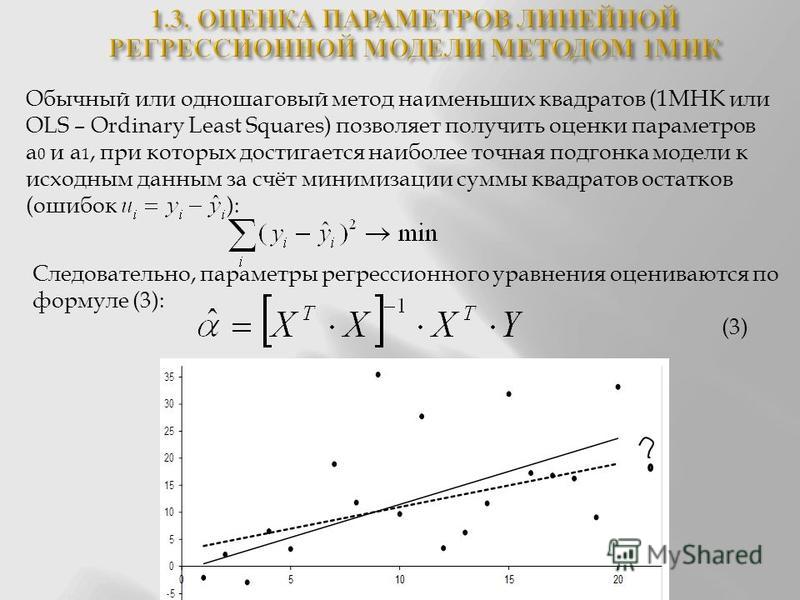
[1] 0.9357
Визуализация моделей
Зададим вид вывода результатов и применим функцию plot к моделям m4 и m6.
# 2 x 2 pictures on one plot and square plotting region, independent of device size
par(mfrow = c(2, 2), pty = "s")
plot(m4)
plot(m6)
Вернем вид вывода результатов к виду по умолчанию
par(mfrow = c(1, 1), pty = "m")
Метод частичных наименьших квадратов (pls)
require(pls)
pls.m1 <- plsr(y ~ ., data=df[train.ids, ], ncomp=2, validation="CV", segments=5, segment.type="random")
Воспользуемся функцией summary для вывода статистики модели
summary(pls.m1)
Data: X dimension: 100 2
Y dimension: 100 1
Fit method: kernelpls
Number of components considered: 2
VALIDATION: RMSEP
Cross-validated using 5 random segments.
(Intercept) 1 comps 2 comps
CV 28.6 13. 2
2
[1] 0.9344
plot(pls.m2)
abline(0, 1)
Метод Random Forest (randomForest)
require(randomForest)
rf.m <- randomForest(y ~ ., data=df[train.ids, ], do.trace=50, mtry=2)
| Out-of-bag |
Tree | MSE %Var(y) |
50 | 37.52 4.68 |
100 | 36.98 4.61 |
150 | 36.74 4.58 |
200 | 35.9 4.48 |
250 | 36.21 4.52 |
300 | 36.34 4.53 |
350 | 36.35 4.54 |
400 | 36.82 4.59 |
450 | 35.87 4.47 |
500 | 35.72 4.46 |
Следует отметить, что большинство функций имеют несколько способов вызова через определение функции как в вышеприведенном случае, либо через указание матрицы X и вектора Y. Так построение модели можно осуществить через
rf.m <- randomForest(x=df[train.ids, -1], y=df[train.ids, "y"], do.trace=50, mtry=2)
Вызовем статистику модели
rf.m
Call:
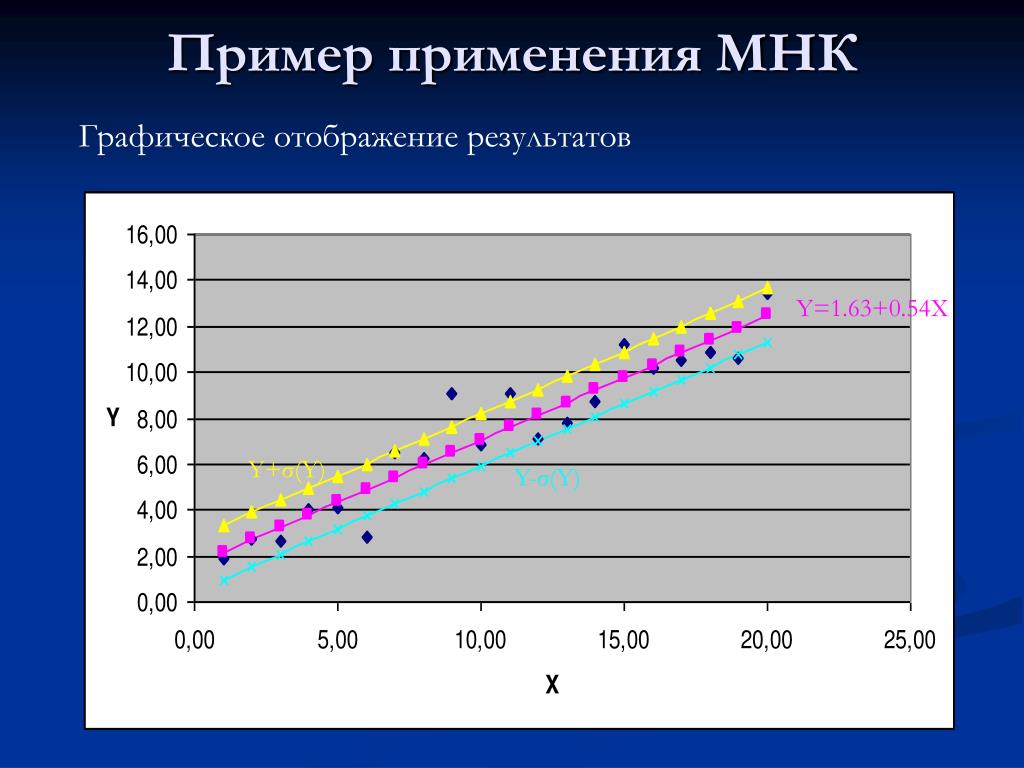
randomForest(formula = y ~ . 2
2
[1] 0.9644
Построим график зависимости между предсказанными и наблюдаемыми значениями
plot(pred.rf, df$y[test.ids])
abline(0, 1)
Решение классификационных задач методом Random Forest
Конвертируем значения y из df в два класса по заданному граничному значению
df$yclass <- factor(ifelse(df$y > 30, 1, 0))
sapply(df, class)
y x1 x2 yclass
"numeric" "numeric" "numeric" "factor"
Построение классификационной модели ничем не отличается от регресссионных моделей. Алгоритм сам выбирает тип модели (скласссификационная или регрессионная) в зависимости от типа данных передаваемого Y. Если Y представлен числовыми значениями, то по умолчанию будет построена регрессионная модель, если Y представлен как factor, то будет построена классификационная модель.
rf.m2 <- randomForest(yclass ~ . - y, data=df[train.ids, ], do.trace=50, mtry=2, importance=TRUE, nPerm=3)
ntree OOB 1 2
50: 4. 00% 3.57% 4.55%
100: 4.00% 3.57% 4.55%
150: 4.00% 3.57% 4.55%
200: 4.00% 3.57% 4.55%
250: 4.00% 3.57% 4.55%
300: 4.00% 3.57% 4.55%
350: 4.00% 3.57% 4.55%
400: 4.00% 3.57% 4.55%
450: 4.00% 3.57% 4.55%
500: 4.00% 3.57% 4.55%
00% 3.57% 4.55%
100: 4.00% 3.57% 4.55%
150: 4.00% 3.57% 4.55%
200: 4.00% 3.57% 4.55%
250: 4.00% 3.57% 4.55%
300: 4.00% 3.57% 4.55%
350: 4.00% 3.57% 4.55%
400: 4.00% 3.57% 4.55%
450: 4.00% 3.57% 4.55%
500: 4.00% 3.57% 4.55%
Обратите внимание на способ представления формулы. Знак минус указывает, что эти переменные должны быть исключены из расммотрения при построении модели.
Выведем статистику модели
rf.m2
Call:
randomForest(formula = yclass ~ . - y, data = df[train.ids, ], do.trace = 50, mtry = 2, importance = TRUE, nPerm = 3)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 2
OOB estimate of error rate: 4%
Confusion matrix:
0 1 class.error
0 54 2 0.03571
1 2 42 0.04545
Проверим прогнозирующую способность на тестовом наборе данных
pred. rf.m2 <- predict(rf.m2, df[test.ids,])
rf.m2 <- predict(rf.m2, df[test.ids,])
Следует помнить, что результатом прогноза будет factor
class(pred.rf.m2)
[1] "factor"
Выведем матрицу ошибок классификации
table(pred.rf.m2, df$yclass[test.ids])
pred.rf.m2 0 1
0 60 6
1 1 33
Выведем значения важности переменных в последней модели
rf.m2$importance
0 1 MeanDecreaseAccuracy MeanDecreaseGini
x1 0.02934 0.002637 0.01767 2.659
x2 0.40098 0.476636 0.42748 46.118
rf.m2$importance[,"MeanDecreaseGini"]
x1 x2
2.659 46.118
Заключение
Следует помнить, что в R реализовано множество различных алгоритмов построения регрессионных и классификационных моделей. Выбор метода построения модели лежит полностью на исследователе и требует некоторого опыта и навыков. Познакомится с некоторыми другими методами машинного обучения, которые присутствуют в R можно по ссылке http://cran. r-project.org/web/views/MachineLearning.html
r-project.org/web/views/MachineLearning.html
Домашнее задание
- Реализовать собственную функцию create.folds для случайного деления выборки на фолды с целью кросс-валидации. Результатом должен быть список, каждый элемент которого содержит индексы соединений, входящих в обучающую выборку отдельного фолда.
- Реализовать случайную генерацию фолдов с возможность ручной инициализации генератора случайных чисел.
- Реализовать генерацию фолдов для отсортированных значений. Таким образом, чтобы фолды были сбалансированы с точки зрения распределения активности.
- Реализовать генерацию фолдов для классификационных задач.
- Реализовать генерацию сбалансированных фолдов для классификационных задач (чтобы количество представителей разных классов в фолдах было приблизительно одинаковым).
- Реализовать все эти подходы в виде одной функции create.folds.
- Осуществить кросс-валидацию для модели randomForest на данных представленных в уроке (df), чтобы сравнить ее с остальными моделями.

- Использовать файл ENB2012_data.xlsx в качестве источника данных (для загрузки данных можно использовать пакет
xlsx). Построить модели зависимости heating.load и Cooling.load от остальных переменных методами, описанными в уроке (можно также поискать другие методы по приведенной в конце занятия ссылке и использовать их).
формулы, код и применение / Хабр
Традиционно в машинном обучении, при анализе данных, перед разработчиком ставится проблема построения объясняющей эти данные модели, которая должна сделать жизнь проще и понятней тому, кто этой моделью начинает пользоваться. Обычно это модель некоторого объекта/процесса, данные о котором собираются при регистрации ряда его параметров. Полученные данные, после выполнения различных подготовительных процедур, представляются в виде таблицы с числовыми данными (где строка – объект, а столбец – параметр), которые необходимо обработать, подставив их в те или иные формулы и посчитать по ним, используя какой-нибудь язык программирования.
Одним из часто встречающихся на практике методе, используемый в самых различных его модификациях, является метод наименьших квадратов (МНК). Этот метод был опубликован в современном виде более двухсот лет назад, именно поэтому особенное удивление вызывает то, что этот хрестоматийным метод не описан максимально подробно на самых популярных ресурсах, просвещённых анализу данных. Поэтому разработчик в попытках самостоятельно разобраться с МНК обращается к чтению самых различных бумажных и электронных изданий. После чего желание разобраться быстро улетучивается по причине того, что авторы этих ресурсов особо не «заморачиваются» над объяснениями выполняемых ими преобразований и допущений.
Обычно объяснение метода представляется в виде:
перегруженного математическими абстракциями «классического описания»;
«готовой процедурки», в которой выполняется программная реализация неких конечных выражений, полученных при каких-то начальных условиях.
Первый вид объяснения вызывает полное отторжение у новичка в виду отсутствия должного уровня математической подготовки и представляется непонятным нагромождением формул. А второй вид представляется неким черным ящиком, из которого чудесным образом извлекаются правильные значения. Из чего делается вывод, что все эти «математические изыскания» лишние, а нужно лишь найти на просторах интернета правильную процедуру и «прикрутить» её в проект, где она начинает выдавать значения «похожие на правильные». Подобный ситуативный путь решения проблемы разработчиком приводит к тому, что корректно проверить, модифицировать найденный код не представляется возможным и, соответственно, верифицировать получаемый результат тоже.
А второй вид представляется неким черным ящиком, из которого чудесным образом извлекаются правильные значения. Из чего делается вывод, что все эти «математические изыскания» лишние, а нужно лишь найти на просторах интернета правильную процедуру и «прикрутить» её в проект, где она начинает выдавать значения «похожие на правильные». Подобный ситуативный путь решения проблемы разработчиком приводит к тому, что корректно проверить, модифицировать найденный код не представляется возможным и, соответственно, верифицировать получаемый результат тоже.
Триада
Данные проблемы возникают из-за того, что при описании МНК не описывается путь перехода от математического описания метода к его программной реализации. Данная проблема была давно преодолена одним из отцов-основателей математического моделирования в нашей стране академиком Самарским А.А., который предложил универсальную методологию вычислительного эксперимента в виде триады «модель-алгоритм-программа».
Из предложенной схемы становится видно, что путь от модели объекта к программе лежит через её алгоритмическое описание. Таким образом, в представленной парадигме для детального объяснения МНК нужно:
Таким образом, в представленной парадигме для детального объяснения МНК нужно:
описать математическую модель объекта/процесса, анализируемые параметры которой формализуются в виде некой функциональной зависимости;
синтезировать алгоритм оценки искомых параметров модели на основе МНК;
выполнить программную реализацию полученного алгоритма.
Попробуем абстракции последних абзацев пояснить на примере. Пусть в качестве моделируемого объекта будем рассматривать процесс измерения термометром температуры печи, которая линейно зависит от времени и флуктуирует в области истинного значения по нормальному закону. Необходимо по выполненным измерениям определить зависимость, по которой изменяется температура в печи. При этом ошибка найденной зависимости должна быть минимальной.
В качестве анализируемых данных будем рассматривать n значений температуры, измеренной в градусах, получаемые с использованием термометра и зависящие от времени. Эти данные представим в виде таблицы, где строки – это объекты, первый столбец – набор параметров (j=1), второй столбец – набор измеренных ответов:
Эти данные представим в виде таблицы, где строки – это объекты, первый столбец – набор параметров (j=1), второй столбец – набор измеренных ответов:
т.е. случайная величина, распределённая по закону Гаусса с фиксированным значением среднеквадратического отклонения (СКО), нулевым математическим ожиданием (МО) и с автокорреляционной функцией в виде дельта-функции.
Ниже приведен код, генерирующий набор данных на python. Для реализации приведенного в статье кода потребуется импортировать несколько библиотек.
import random
import matplotlib.pyplot as plt
import numpy as np
def datasets_make_regression(coef, data_size, noise_sigma, random_state):
x = np.arange(0, data_size, 1.)
mu = 0.0
random.seed(random_state)
noise = np.empty((data_size, 1))
y = np.empty((data_size, 1))
for i in range(data_size):
noise[i] = random.gauss(mu, noise_sigma)
y[i] = coef[0] + coef[1]*x[i] + noise[i]
return x, y
coef_true = [34. 2, 2.] # весовые коэффициенты
data_size = 200 # размер генерируемого набора данных
noise_sigma = 10 # СКО шума в данных
random_state = 42
x_scale, y_estimate = datasets_make_regression(coef_true, data_size, noise_sigma, random_state)
plt.plot(x_scale, y_estimate, 'o')
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)
2, 2.] # весовые коэффициенты
data_size = 200 # размер генерируемого набора данных
noise_sigma = 10 # СКО шума в данных
random_state = 42
x_scale, y_estimate = datasets_make_regression(coef_true, data_size, noise_sigma, random_state)
plt.plot(x_scale, y_estimate, 'o')
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)Сгенерированный набор данных будет иметь вид
Рисунок 1 – Зависимость температуры от времениМатематическая модель
Далее математическая модель будет описана три раза. Последовательно уровень абстракции при описании модели будет понижаться и конкретизироваться. Эти описания приведены для того, чтобы в дальнейшем материал, приведенный в статье, можно было соотнести с классическими изданиями.
Первое описание математической модели. Самое общее.
Поскольку мы рассматриваем процесс, который связывает набор наблюдаемых параметров и измеренных ответов с минимальной ошибкой этой связи, то математическую модель этого процесса в общем виде можно представить
Второе описание математической модели.
 Общее описание линейной модели.
Общее описание линейной модели.Поскольку по условию задачи мы рассматриваем линейную зависимость, на которую влияет шум, имеющий нормальное распределение с нулевым средним значением, то используем линейную относительно параметров модель, а метрикой выберем расчёт СКО ошибки
Третье описание математической модели. Модель конкретизирована под условия примера.
Поскольку по условию задачи мы рассматриваем линейную зависимость одного параметра (поскольку j=1, то далее эту зависимость при описании опустим), на оценку которого влияет шум, имеющий нормальное распределение, то используем линейную модель с двумя коэффициентами
Обсуждение моделей
Было рассмотрено три модели, описывающих процесс изменения температуры в печи. Первая модель описана в наиболее общем виде, а третья приведена в виде, наиболее соответствующем начальным условиям задачи. В третьей модели учтен линейный закон изменения температуры (используется линейная модель) и нормальный закон распределения шума в измерениях (используется квадратичная функция ошибки).
Хочется отметить, что параметры математической модели процесса изменения температуры, описанной в выражении (2), в принципе, могут находиться не только методом наименьших квадратов, поскольку метрика с квадратичной функцией ошибки в явном виде не прописана. Такая общая форма записи приведена, поскольку не представляется возможным в кратком виде привести все возможные модификации МНК, у которого минимизация для различных условий может выполняться также различно.
В выражениях (3) и (4) линейные модели отличаются только количеством учитываемых параметров, причем третья модель – это редуцированная вторая модель, у которой только два коэффициента (один свободный и один весовой коэффициенты).
Далее с использованием выражения (4) и МНК, синтезируем алгоритмы, оценивающие параметры модели.
Алгоритмы и реализующие их программы
Далее будут выведены три алгоритма, результат работы которых позволит определить зависимость изменения температуры печи от времени. Последовательно сложность конечных выражений, используемых в алгоритмах, будет понижаться. Эти алгоритмы приведены для того, чтобы полученные выражения, можно было соотнести с классическими изданиями.
Последовательно сложность конечных выражений, используемых в алгоритмах, будет понижаться. Эти алгоритмы приведены для того, чтобы полученные выражения, можно было соотнести с классическими изданиями.
Начнем с применения правила дифференцирования функции представленной в виде суммы
применим правило дифференцирования сложной функции
применим правило дифференцирования функции представленной в виде суммы
применим правило дифференцирования функции представленной в виде суммы
Приравняем полученные производные к нулю и решим полученную систему уравнений
Раскроем скобки
Вынесем постоянные множители за скобки
Вынесем слагаемые с множителем «y» в правую часть уравнений
Поставим слагаемые с множителем «x» в левой части в порядке убывания степеней
Для решения полученной системы алгебраических уравнения представим её в матричной форме
Выразим вектор w* с искомыми весами выполнив умножение обеих частей равенства на обратную матрицу y
Полученное выражение (5) является решением системы уравнений и его можно уже использовать в качестве первого алгоритма оценки параметров модели. Ниже приведен код реализующий этот алгоритм.
Ниже приведен код реализующий этот алгоритм.
def coefficient_reg_inv(x, y):
size = len(x)
# формируем и заполняем матрицу размерностью 2x2
A = np.empty((2, 2))
A[[0], [0]] = sum((x[i])**2 for i in range(0,size))
A[[0], [1]] = sum(x)
A[[1], [0]] = sum(x)
A[[1], [1]] = size
# находим обратную матрицу
A = np.linalg.inv(A)
# формируем и заполняем матрицу размерностью 2x1
C = np.empty((2, 1))
C[0] = sum((x[i]*y[i]) for i in range(0,size))
C[1] = sum((y[i]) for i in range(0,size))
# умножаем матрицу на вектор
ww = np.dot(A, C)
return ww[1], ww[0]
[w0_1, w1_1] = coefficient_reg_analit(x_scale, y_estimate)
print(w0_1, w1_1)Результат работы алгоритма:
[33.93193341] [2.01436546]
Выражение (5) можно упростить, выполнив аналитический расчет обратной матрицы.
Найти обратную матрицу можно с использованием, например, алгебраических дополнений. Для пояснения поиска обратной матрицы введем новую переменную A. Пусть
Пусть
Перепишем выражение (5) в виде
Упростим выражение раскрыв скобки, чтобы получить более компактную форму записи
Теперь решение системы уравнений имеет вид
Полученное выражение (6) можно использовать в качестве второго алгоритма оценки параметров модели. Ниже приведен код, реализующий этот алгоритм.
def coefficient_reg_inv_analit(x, y):
size = len(x)
# выполним расчет числителя первого элемента вектора
numerator_w1 = size*sum(x[i]*y[i] for i in range(0,size)) - sum(x)*sum(y)
# выполним расчет знаменателя (одинаковый для обоих элементов вектора)
denominator = size*sum((x[i])**2 for i in range(0,size)) - (sum(x))**2
# выполним расчет числителя второго элемента вектора
numerator_w0 = -sum(x)*sum(x[i]*y[i] for i in range(0,size)) + sum((x[i])**2 for i in range(0,size))*sum(y)
# расчет искомых коэффициентов
w1 = numerator_w1/denominator
w0 = numerator_w0/denominator
return w0, w1
[w0_2, w1_2] = coefficient_reg_inv_analit(x_scale, y_estimate)
print(w0_2, w1_2)Результат работы алгоритма:
[33. 93193341] [2.01436546]
93193341] [2.01436546]
Видно, что полученный результат совпадает с результатом, полученным с использованием выражения (5).
Выполним дальнейшее упрощение полученного выражения (6), чтобы получить более компактную форму записи.
раскроем скобки:
Ведем новые переменные используя термины математической статистики:
С учётом введённых переменных искомый вектор w* примет вид
Таким образом итоговое выражение представим в виде:
Полученное выражение (7) можно использовать в качестве третьего алгоритмаоценки параметров модели. Ниже приведен код, реализующий этот алгоритм.
def coefficient_reg_stat(x, y):
size = len(x)
avg_x = sum(x)/len(x) # оценка МО величины x
avg_y = sum(y)/len(y) # оценка МО величины y
# оценка МО величины x*y
avg_xy = sum(x[i]*y[i] for i in range(0,size))/size
# оценка СКО величины x
std_x = (sum((x[i] - avg_x)**2 for i in range(0,size))/size)**0.5
# оценка СКО величины y
std_y = (sum((y[i] - avg_y)**2 for i in range(0,size))/size)**0. 5
# оценка коэффициента корреляции величин x и y
corr_xy = (avg_xy - avg_x*avg_y)/(std_x*std_y)
# расчет искомых коэффициентов
w1 = corr_xy*std_y/std_x
w0 = avg_y - avg_x*w1
return w0, w1
[w0_3, w1_3] = coefficient_reg_stat(x_scale, y_estimate)
print(w0_3, w1_3)
5
# оценка коэффициента корреляции величин x и y
corr_xy = (avg_xy - avg_x*avg_y)/(std_x*std_y)
# расчет искомых коэффициентов
w1 = corr_xy*std_y/std_x
w0 = avg_y - avg_x*w1
return w0, w1
[w0_3, w1_3] = coefficient_reg_stat(x_scale, y_estimate)
print(w0_3, w1_3)Результат работы алгоритма:
[33.93193341] [2.01436546]
Сравним полученные значения с результатом работы процедуры библиотеки sklearn.
from sklearn.linear_model import LinearRegression
# преобразование размерности массива x_scale для корректной работы model.fit
x_scale = x_scale.reshape((-1,1))
model = LinearRegression()
model.fit(x_scale, y_estimate)
print(model.intercept_, model.coef_)
Результат работы алгоритма:
[33.93193341] [2.01436546]
Видно, что полученный результат полностью совпадает с результатами, полученными ранее.
Итак, визуализируем полученный результат, построив прямую с использованием рассчитанных коэффициентов и сопоставим их с исходными данными (рисунок 2).
def predict(w0, w1, x_scale):
y_pred = [w0 + val*w1 for val in x_scale]
return y_pred
y_predict = predict(w0_1, w1_1, x_scale)
plt.plot(x_scale, y_estimate, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_predict, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)Рисунок 2 – Зависимость температуры от времениОбсуждение алгоритмов
Таким образом удалось выполнить оценку параметров модели, которая описывает процесс изменения температуры в печи с минимальной ошибкой. Выведенные выражения (5) – (7) и запрограммированные по ним три алгоритма, реализующие МНК при обработке одного набора измеренных температур, хотя и отличаются видом конечных выражений, дают одинаковые оценки. Последовательный вывод выражений, выполненный в статье, показывает, что эти выражения по сути «делают» одно и тоже, однако, позволяют давать различные интерпретации. При этом хочется отметить, что в алгоритмах (6) – (7) удалось уйти от процедуры обращения матрицы, которая при обработке реальных данных может выполняться нестабильно.
При этом хочется отметить, что в алгоритмах (6) – (7) удалось уйти от процедуры обращения матрицы, которая при обработке реальных данных может выполняться нестабильно.
Ещё один пример. Анализируем остатки.
количество выбросов в выборке равно 10;
длительность импульса равна 1-му измерению;
амплитуда импульса равна 256;
позиция первого импульса соответствует 10-му измерению;
период следования импульсов – каждые 20 измерений.
ni = 10 # количество выбросов
ind_impuls = np.arange(ni, data_size, 20) # индексы выбросов
y_estimate_imp = y_estimate.copy() # выборка с выбросами
for i in range(0, ni):
y_estimate_imp[ind_impuls[i]] += 256
[w0_imp, w1_imp] = coefficient_reg_stat(x_scale, y_estimate_imp)
y_pred_imp = predict(w0_imp, w1_imp, x_scale)
plt.plot(x_scale, y_estimate_imp, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_pred_imp, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt. xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)
xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14) Рисунок 3 – Зависимость температуры от времениНа рисунке 3 видно, что появление выбросов сместило, рассчитанную по выражению (7) прямую в вверх. Модифицируем алгоритм оценки параметров модели за счет новой метрики, а именно оценки квадратов разности между измеренными и модельными данными, которая выполняется по выражению
Ниже приведен код, который выполняет этот расчет (8) и визуализирует полученный результат (рисунок 4).
SqErr = (y_pred_imp - y_estimate_imp)**2
plt.plot(x_scale, SqErr, 'o')
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('Квадрат ошибки', fontsize=14)Рисунок 4 – Оценка квадратов разности между измеренными и модельными даннымиДля устранения влияния помехи на оценки параметров модели, получаемых с использованием алгоритмов, дополнительно введем процедуру цензурирования (отбрасывания) данных, которые имеют большое значение квадрата ошибки (8). С новыми начальными условиями алгоритм оценки параметров модели теперь дополняется следующей последовательностью действий
С новыми начальными условиями алгоритм оценки параметров модели теперь дополняется следующей последовательностью действий
def censor_data(SqErr, nCensor):
# индексы отсортированного во возрастанию массива с квадратами ошибок
I = np.argsort(SqErr[:,0])
ind_imp = I[-nCensor:]
ind_imp = ind_imp[::-1] # разворот индексов массива
w0 = np.empty((nCensor, 1))
w1 = np.empty((nCensor, 1))
for i in range(0,nCensor):
# цензурирование данных
x_scale_cens = np.delete(x_scale, ind_imp[0:i], 0)
y_estimate_imp_cens = np.delete(y_estimate_imp, ind_imp[0:i], 0)
# расчёт параметров модельной прямой
w0[i], w1[i] = coefficient_reg_stat(x_scale_cens, y_estimate_imp_cens)
y_pred2_cens = predict(w0[i], w1[i], x_scale_cens)
return w0, w1
nCensor = 20 # количество отбрасываемых выбросов
[w0_с, w1_с] = censor_data(SqErr, nCensor)
plt.plot(coef_true[0], coef_true[1], 'o', label = 'Истинные значения')
plt.plot(w0_с, w1_с, '-*', label = 'Расчетные значения')
plt. legend(loc = 'best', fontsize=12)
plt.xlim((30, 50))
plt.ylim((1.85, 2.15))
plt.xlabel('w0', fontsize=18)
plt.ylabel('w1', fontsize=18)
legend(loc = 'best', fontsize=12)
plt.xlim((30, 50))
plt.ylim((1.85, 2.15))
plt.xlabel('w0', fontsize=18)
plt.ylabel('w1', fontsize=18)По итогам работы алгоритма построим полученные оценки параметров модели (рисунок 5) по мере цензурирования данных.
Рисунок 5 – Оценки параметров модели по мере цензурирования данныхВ результате работы рассматриваемого алгоритма видно (рисунок 5), что по мере цензурирования помеховых данных параметры модели приближаются к истинным (точка с оценкой параметров возле i=1 получена после удаления первой точки, точка с оценкой параметров возле i=20 получена после удаления двадцатой точки).
Ниже приведен код, который рассчитывает и строит на графике прямую (рисунок 6) с использованием параметров модели, полученной на последнем шаге алгоритма c цензурированием. На этом рисунке видно, что использование дополнительной процедуры цензурирования данных на основе анализа остаточной суммы квадратов, позволяет улучшить согласование оцениваемых параметров с истинными.
y_pred_censor = predict(w0_с[nCensor-1], w1_с[nCensor-1], x_scale)
plt.plot(x_scale, y_estimate_imp, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_pred_censor, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt.xlabel('X (порядковый номер измерения)', fontsize=14)
plt.ylabel('Y (оценка температуры)', fontsize=14)Рисунок 6 – Зависимость температуры от времениОбсуждение алгоритма
Был рассмотрен алгоритм оценки параметров модели, которая описывает процесс изменения температуры в печи при наличии помех в измерениях. Показано, как зная логику построения алгоритма его можно модифицировать под изменившиеся условия и получить необходимый результат (оценку параметров модели).
Безусловно, что приведенный в статье алгоритм оценки параметров модели с использованием процедуры цензурирования импульсных помеховых сигналов (в том виде, в котором он приведен в статье) не является оптимальным и универсальным. Он приведен здесь для иллюстрации возможностей модификации алгоритма, реализующего классический МНК. А также для демонстрации ещё одной важной метрики при использовании МНК – оценка квадратов разности между измеренными и модельными данными (8), которая является источником множества различных модификаций метода.
А также для демонстрации ещё одной важной метрики при использовании МНК – оценка квадратов разности между измеренными и модельными данными (8), которая является источником множества различных модификаций метода.
Заключение
В статье делается попытка «расколдовать» классический МНК, а также продемонстрировать удобство методологической интерпретации решения задачи в виде триады «модель-алгоритм-программа», которая позволяет осуществить бесшовный переход от модельной постановки задачи и задания начальных условий до её программной реализации. Ставилась задача в максимально доступной для читателя форме продемонстрировать последовательность математической мысли при решении задачи с применением МНК. Показать, как начальные условия влияют на полученные конечные выражения. Автор надеется, что статья будет полезной для всех тех, кто при решении различных задач анализа данных попытается применить или модифицировать классические методы и для этого попробует также с «карандашом в руках» выполнить вывод конечных выражений. Этот подход позволит разработчику применять на практике понятные для него алгоритмы, а не код, который работает «по неведомым» правилам.
Этот подход позволит разработчику применять на практике понятные для него алгоритмы, а не код, который работает «по неведомым» правилам.
Урок 1: Линейная регрессия методом наименьших квадратов в R
Цели:
AP Студенты, изучающие статистику, будут использовать R для исследования модели линейной регрессии методом наименьших квадратов между двумя переменными, объясняющей (входной) переменной и ответной (выходной) переменной. Вы научитесь определять, какая независимая переменная поддерживает самую сильную линейную связь с переменной отклика. Вы изучите графики данных и остаточные графики для LSLR с одной переменной на предмет соответствия. Остаточные графики будут проверены на наличие закономерностей, которые могут указывать на нарушение лежащих в основе допущений.
Простая модель линейной регрессии
Сначала мы изучим набор данных с двумя переменными, чтобы определить линейную связь между двумя атрибутами отдельных лиц или объектов в совокупности. Хотя не имеет значения, какая переменная считается x при оценке силы связи, она имеет значение, когда мы устанавливаем регрессионную модель. Помните, что мы обычно используем x как объясняющую переменную, а y как переменную отклика. В R вы можете присвоить своим переменным любое имя, которое вы выберете.
Хотя не имеет значения, какая переменная считается x при оценке силы связи, она имеет значение, когда мы устанавливаем регрессионную модель. Помните, что мы обычно используем x как объясняющую переменную, а y как переменную отклика. В R вы можете присвоить своим переменным любое имя, которое вы выберете.
Напомним, что строка LSLR записывается в виде y=α+ βx. Если объясняющая переменная является точным предиктором переменной отклика, то отклонения от линии не будет. Часто это не так. Линия LSLR называется «линией наилучшего соответствия», потому что она сводит к минимуму количество вариаций или ошибок каждого наблюдения из подобранной линии. Таким образом, истинная модель записывается как y = α + βx + ε, где ε представляет собой отклонение от наблюдаемого значения переменной отклика до прогнозируемого значения переменной отклика. Вы должны распознавать эти ошибки как остатки.
Проблема
SENIC — это исследование эффективности контроля за внутрибольничными инфекциями, целью которого было определить, снизили ли программы надзора и контроля за инфекциями показатели внутрибольничных (внутрибольничных) инфекций в больницах США. Этот набор данных состоит из 113 случайно выбранных больниц из первоначальных 338 обследованных больниц. Статистические данные представляют собой либо средние значения для больницы за период исследования, либо коэффициенты для больницы, основанные на общей частоте в течение периода исследования. Ни одна из этих переменных не является категориальной.
Этот набор данных состоит из 113 случайно выбранных больниц из первоначальных 338 обследованных больниц. Статистические данные представляют собой либо средние значения для больницы за период исследования, либо коэффициенты для больницы, основанные на общей частоте в течение периода исследования. Ни одна из этих переменных не является категориальной.
Заголовки для каждого столбца:
- Пребывание = средняя продолжительность пребывания всех пациентов в больнице в днях
- Риск = средняя оценочная вероятность заражения в больнице (в процентах) (обычно это значение y)
- Возраст = средний возраст пациентов (в годах)
- Посев = отношение числа выполненных посевов к числу пациентов без признаков или симптомов внутрибольничной инфекции, умноженное на 100.
- X.Ray = отношение количества выполненных рентгенограмм к количеству пациентов без признаков или симптомов пневмонии, умноженное на 100.
- Койки = среднее количество коек в больнице за период исследования
Источник: Прикладные линейные статистические модели, 3-е изд. , Нетер Дж., Вассерман В., Катнер М. (Бостон, 1990 г.) Приложение B
, Нетер Дж., Вассерман В., Катнер М. (Бостон, 1990 г.) Приложение B
Первые задачи
- Общий каталог в папке статистики AP. Используйте getwd(), чтобы определить, какой каталог R использует в данный момент. Чтобы изменить рабочий каталог, используйте раскрывающееся меню в разделе «Файл» и найдите папку R, которую вы хотите использовать.
- Загрузите первый набор данных — он называется «senic.dat». Используйте команду read.table для загрузки этих данных в R и измените имя файла данных на более подходящее для использования:
senic<-read.table("senic.dat", header = T) - Введите имя файла данных в R, что приведет к дампу данных.
сенич
Если вы не получили дамп данных, значит, файл данных неправильно загружен в рабочий каталог R.
- Обратите внимание на имена всех переменных и их тип — R чувствителен к регистру!!
- Измените имена переменных с помощью следующих команд:
stay ← senic$Stay риск ← senic$Риск возраст ←senic$Возраст лаборатория ←senic$Культура рентген ← сенник $ X.
 Ray
кровати ←senic$Кровати
Ray
кровати ←senic$Кровати
Эти сокращенные имена облегчат работу в лаборатории.
Файлы данных и графики данных
Мы начнем это упражнение с построения графика набора данных с помощью plot() команда:
plot( имя файла$variable1, имя файла$variable2 )
Поскольку мы уже сократили имена, используйте эту команду:
участок( пребывание, риск )
Помните, что ваш график должен иметь переменную отклика по вертикальной оси и объясняющую переменную по горизонтальной оси. R автоматически подгонит масштаб данных для каждой оси для всех графиков.
Ваш график должен выглядеть так, как показано ниже.
Обратите внимание, что выходные данные включают метки по осям x и y в том же формате, что и переменные, которые вы использовали в команде построения графика. Если вы хотите изменить эти метки, вы можете сделать это и сделать их более соответствующими набору данных. Вы также можете добавить заголовок к графику. Все это можно сделать одновременно с помощью команды plot.
Вы также можете добавить заголовок к графику. Все это можно сделать одновременно с помощью команды plot.
plot(пребывание, риск, xlab="Продолжительность пребывания", ylab="Риск заражения", main="Риск внутрибольничной инфекции")
Здесь, xlab — это метка оси X, а ylab — метка оси Y. Заголовок графика создается с помощью основной команды. Метки и заголовок вводятся с двойными кавычками.
Более профессионально выглядящая диаграмма рассеяния находится на следующей странице.
Для практики создайте как минимум две диаграммы рассеяния с разными независимыми переменными из набора данных. Не забудьте указать полные метки для осей и заголовка. Если вы хотите сохранить свой график, вы можете щелкнуть его правой кнопкой мыши и скопировать как растровое изображение. Затем вставьте график в Word и сохраните файл Word. Первая диаграмма рассеяния должна выглядеть так:
Второй график должен выглядеть так:
Линейная регрессия методом наименьших квадратов
Далее вы запустите простую линейную регрессию с двумя переменными из этого набора данных. Вы хотите найти предиктор риска внутрибольничной инфекции, переменную Risk из набора данных SENIC. Вы можете рассмотреть длину, возраст, лабораторию, сундук или кровати в качестве независимой переменной. Вы уже построили диаграмму рассеяния риска и продолжительности пребывания на первом графике, и она выглядит примерно линейной, так что давайте рассмотрим эту взаимосвязь.
Вы хотите найти предиктор риска внутрибольничной инфекции, переменную Risk из набора данных SENIC. Вы можете рассмотреть длину, возраст, лабораторию, сундук или кровати в качестве независимой переменной. Вы уже построили диаграмму рассеяния риска и продолжительности пребывания на первом графике, и она выглядит примерно линейной, так что давайте рассмотрим эту взаимосвязь.
Команда для простой линейной регрессии — lm(переменная ответа~независимая переменная).
лм(риск~пребывание)
Вот вывод этой команды:
Коэффициенты: (Перехват) остаться 0,7437 0,3742
Как бы вы интерпретировали этот вывод? ____________________________________________________________________
Что такое уравнение LSLR?__________________________________________________________________________
Назовем эту модель1. Запустите команду для создания model1:
model1< lm(risk~stay)
Затем введите команду model1$fitted. values
values
Что означают эти числа?
1 2 3 4 5 6 7 8 3,411654 4,044034 3,864423 4,092679 4,934605 4,395772 4,365837 4,927122 9 10 11 12 13 14 15 16 3,987906 4,051518 4,885961 3,849456 5,525825 3,580039 4,111388 4,889703 17 18 19 20 21 22 23 24 3,841972 5,091765 4,133840 4,242355 3,561330 4,575383 4,403256 4,425707 25 26 27 28 29 30 31 32 4,186226 3,841972 4,227387 3,808295 5,102991 4,444417 4,870993 4,425707 33 34 35 36 37 38 39 40 5,147893 5,828918 4,388289 4,609060 4,474352 3,677328 4,661447 3,797069 41 42 43 44 45 46 47 48 3,916810 4,754994 4,934605 4,530481 3,875649 4,545448 8,062830 4,822348 49 50 51 52 53 54 55 56 3,613716 4,066485 5,039378 4,197452 5,013185 5,260150 3,972938 4,915896 57 58 59 60 61 62 63 64 3,415396 3,606232 4,758736 5,031895 4,642737 4,927122 3,711005 4,358353 65 66 67 68 69 70 71 72 3,654877 4,268548 4,493062 3,954229 4,339644 3,748424 3,508943 3,392944 73 74 75 76 77 78 7980 4,309709 4,504287 3,905584 3,250752 4,073969 4,571641 4,066485 4,597835 81 82 83 84 85 86 87 88 4,781188 3,714747 3,598749 4,025325 3,770876 4,130098 3,703522 4,631512 89 90 91 92 93 94 95 96 4,246096 5,013185 4,059002 4,085195 4,081453 3,793327 4,399514 3,939261 97 98 99 100 101 102 103 104 3,984164 5,237699 3,718489 4,541706 4,395772 4,444417 3,415396 5,963627 105 106 107 108 109 110 111 112 4,276032 4,784929 3,415396 3,744682 5,159119 4,298483 3,624942 7,456643 113 4.264806
Эти значения являются предсказанными значениями y ( y ) на основе LSLR! Давайте сократим предсказанные значения y до yfit:
yfit<-model1$fitted.values
Прежде чем вы сможете нанести линию модели на диаграмму рассеяния, она должна быть доступна.
участок(пребывание, риск)
Чтобы нанести модель на диаграмму рассеивания, используйте команду:
линий (остаться, yfit)
Результат должен выглядеть, как на графике ниже.
Ну, это выглядит примерно линейно. Давайте рассмотрим остаточный график. Помните, что невязка — это разница между наблюдаемым значением y при некотором конкретном значении x и предсказанным значением y при том же значении x.
Остаток = А-А.
Значения y здесь — это значения риска, а прогнозируемые значения — это значения, связанные с yfit . Определите переменную resid, как описано ниже, затем постройте график x-переменной в зависимости от остатка.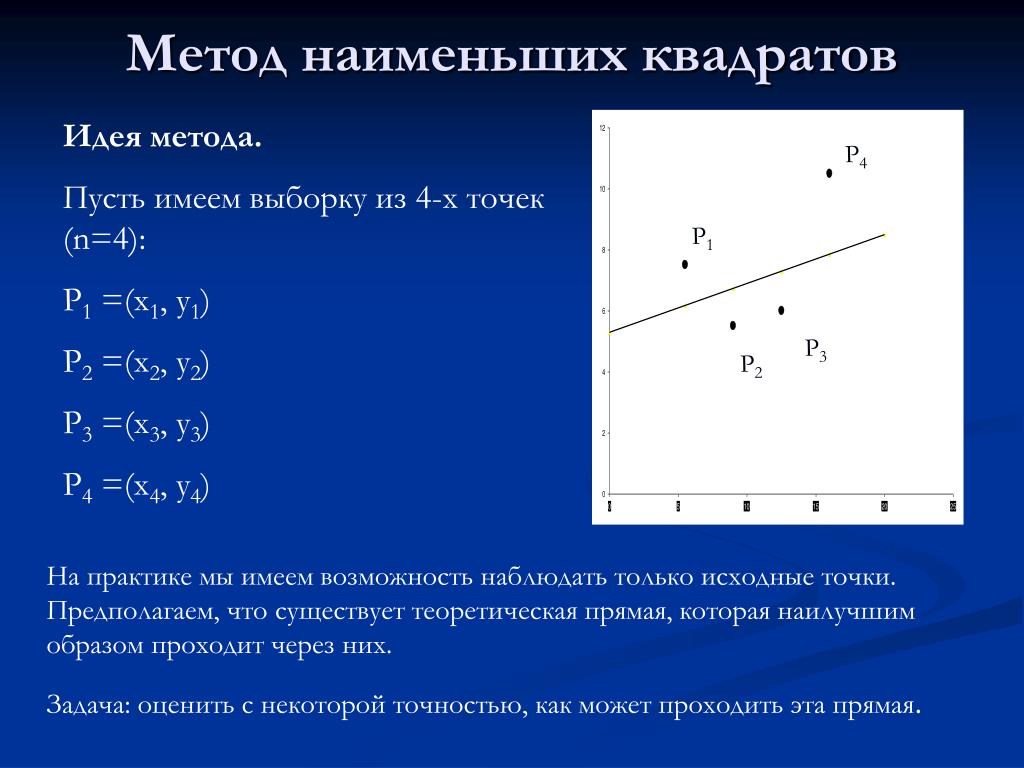
остаток ← риск – yfit
участок (для проживания, проживания)
Итак… остаточный сюжет говорит вам о чем-нибудь? Опишите здесь то, что вы видите на графике.
Наконец, давайте посмотрим на коэффициент корреляции для этой конкретной модели:
cor(stay, risk)
Какое значение вы получили для r? Как бы вы интерпретировали это значение в контексте проблемы?
Дополнительные файлы:
Линия регрессии методом наименьших квадратов — Примечания для учителя
5.2 Оценка методом наименьших квадратов | Прогнозирование: принципы и практика (2-е изд.)
На практике, конечно, у нас есть набор наблюдений, но мы не знаем значений коэффициентов \(\beta_0,\beta_1, \dots, \beta_k\). Их необходимо оценить по данным.
Принцип наименьших квадратов позволяет эффективно выбирать коэффициенты, сводя к минимуму сумму квадратов ошибок. 2.
\]
2.
\]
Это называется оценкой наименьших квадратов , поскольку она дает наименьшее значение суммы квадратов ошибок. Поиск наилучших оценок коэффициентов часто называют «подгонкой» модели к данным, а иногда «обучением» или «обучением» модели. Таким образом была получена линия, показанная на рис. 5.3.
Когда мы ссылаемся на оцененных коэффициентов, мы будем использовать обозначение \(\hat\beta_0, \dots, \hat\beta_k\). Уравнения для них будут даны в разделе 5.7.
Функция tslm() сопоставляет модель линейной регрессии с данными временных рядов. Она аналогична функции lm() , которая широко используется для линейных моделей, но tslm() предоставляет дополнительные возможности для обработки временных рядов.
Пример: расходы на потребление в США
Модель множественной линейной регрессии для потребления в США
\[
y_t=\beta_0 + \beta_1 x_{1,t}+ \beta_2 x_{2,t}+ \beta_3 x_{3,t}+ \beta_4 x_{4,t}+\varepsilon_t,
\]
где \(y\) - процентное изменение реальных расходов на личное потребление, \(x_1\) - процентное изменение реального личного располагаемого дохода, \(x_2\) - процентное изменение промышленного производства, \(x_3\) - процентное изменение личных сбережений и \(x_4\) - изменение уровня безработицы.
Следующий вывод предоставляет информацию о установленной модели. В первом столбце таблицы Коэффициенты дается оценка каждого коэффициента \(\бета\), а во втором столбце - его стандартная ошибка (т. наборы данных). Стандартная ошибка дает меру неопределенности в оцененном коэффициенте \(\beta\).
фит.consMR <- tslm( Потребление ~ Доход + Производство + Безработица + Сбережения, данные=обмен) резюме (fit.consMR) #> #> Вызов: #> tslm(formula = Потребление ~ Доход + Производство + Безработица + #> Экономия, данные = uschange) #> #> Остатки: #> Мин. 1 кв. Медиана 3 кв. Макс. #> -0,8830 -0,1764 -0,0368 0,1525 1,2055 #> #> Коэффициенты: #> Оценить стд. Значение ошибки t Pr(>|t|) #> (Перехват) 0,267290,03721 7,18 1,7э-11*** #> Доход 0,71448 0,04219 16,93 < 2e-16 *** #> Производство 0,04589 0,02588 1,77 0,078 . #> Безработица -0,20477 0,10550 -1,94 0,054 . #> Экономия -0,04527 0,00278 -16,29 < 2e-16 *** #> --- #> Обозначение. коды: #> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0,1 '' 1 #> #> Остаточная стандартная ошибка: 0,329 на 182 степенях свободы #> Множественный R-квадрат: 0,754, скорректированный R-квадрат: 0,749 #> F-статистика: 139на 4 и 182 DF, p-значение: <2e-16
Для целей прогнозирования последние два столбца представляют ограниченный интерес. «Значение t» представляет собой отношение оценочного коэффициента \(\beta\) к его стандартной ошибке, а в последнем столбце указано p-значение: вероятность того, что оценочный коэффициент \(\beta\) будет настолько большим, насколько это возможно если бы не было реальной связи между потреблением и соответствующим предиктором. Это полезно при изучении влияния каждого предиктора, но не особенно полезно для прогнозирования.
Подобранные значения
Предсказания \(y\) можно получить, используя оценочные коэффициенты в уравнении регрессии и установив член ошибки равным нулю. В общем пишем,
\[\начало{уравнение}
\hat{y}_t = \hat\beta_{0} + \hat\beta_{1} x_{1,t} + \hat\beta_{2} x_{2,t} + \cdots + \hat\beta_ {к} х_{к, т}. \тег{5.2}
\конец{уравнение}\]
Подстановка значений \(x_{1,t},\dots,x_{k,t}\) для \(t=1,\dots,T\) возвращает прогнозы \(y_t\) в рамках обучения- образец, именуемый подобранные значения . Обратите внимание, что это прогнозы данных, используемых для оценки модели, а не подлинные прогнозы будущих значений \(y\).
\тег{5.2}
\конец{уравнение}\]
Подстановка значений \(x_{1,t},\dots,x_{k,t}\) для \(t=1,\dots,T\) возвращает прогнозы \(y_t\) в рамках обучения- образец, именуемый подобранные значения . Обратите внимание, что это прогнозы данных, используемых для оценки модели, а не подлинные прогнозы будущих значений \(y\).
На следующих графиках показаны фактические значения по сравнению с подобранными значениями для процентного изменения в ряду потребительских расходов в США. Временной график на рис. 5.6 показывает, что подогнанные значения довольно точно соответствуют фактическим данным. Это подтверждается сильной положительной взаимосвязью, показанной на диаграмме рассеяния на рис. 5.7.
автоплот(uschange['Потребление'], серия="Данные") +
автоуровень (подогнанный (fit.consMR), серия = «Подогнанный») +
xlab("Год") + ylab("") +
ggtitle("Процентное изменение потребительских расходов в США") +
направляющие(цвет=guide_legend(title=" ")) Рисунок 5.6: График фактических потребительских расходов в США и прогнозируемых потребительских расходов в США во времени.
cbind(Данные = uschange["Потребление"],
Установлено = установлено (fit.consMR)) %>%
as.data.frame() %>%
ggplot(aes(x=данные, y=установлено)) +
геометрическая_точка() +
ylab("Подобранные (прогнозируемые значения)") +
xlab("Данные (фактические значения)") +
ggtitle("Процентное изменение потребительских расходов в США") +
geom_abline (перехват = 0, наклон = 1) Рисунок 5.7: График фактических потребительских расходов в США в сравнении с прогнозируемыми потребительскими расходами в США. 92\) значение 0,16, полученное из простой регрессии с тем же набором данных в разделе 5.1. Добавление трех дополнительных предикторов позволило объяснить гораздо больше различий в данных о потреблении.
Стандартная ошибка регрессии
Еще одним показателем того, насколько хорошо модель соответствует данным, является стандартное отклонение остатков, которое часто называют «остаточной стандартной ошибкой». Это показано в приведенном выше выводе со значением 0,329. 2}},
\тег{5.3}
\конец{уравнение}\]
где \(k\) - количество предикторов в модели. Обратите внимание, что мы делим на \(T-k-1\), потому что мы оценили параметры \(k+1\) (отрезок и коэффициент для каждой переменной-предиктора) при вычислении остатков.
2}},
\тег{5.3}
\конец{уравнение}\]
где \(k\) - количество предикторов в модели. Обратите внимание, что мы делим на \(T-k-1\), потому что мы оценили параметры \(k+1\) (отрезок и коэффициент для каждой переменной-предиктора) при вычислении остатков.
Стандартная ошибка связана с размером средней ошибки, которую производит модель. Мы можем сравнить эту ошибку со средним значением выборки \(y\) или со стандартным отклонением \(y\), чтобы получить некоторое представление о точности модели.
Стандартная ошибка будет использоваться при генерации интервалов прогнозирования, описанных в разделе 5.6.
Обыкновенные наименьшие квадраты (OLS) Линейная регрессия в R
[Эта статья была впервые опубликована на Экологическая наука и анализ данных и любезно посодействовал R-блогерам]. (Вы можете сообщить о проблеме с содержанием на этой странице здесь)
Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.

Линейная регрессия методом наименьших квадратов (OLS) — это статистический метод, используемый для анализа и моделирования линейных отношений между переменной ответа и одной или несколькими переменными-предикторами. Если взаимосвязь между двумя переменными кажется линейной, то для моделирования взаимосвязи к данным можно подобрать прямую линию. Линейное уравнение (или уравнение прямой) для двумерной регрессии принимает следующий вид:
, где y — переменная отклика (зависимая), m — градиент (наклон), x — переменная-предиктор (независимая), а c — точка пересечения. Применение моделирования линейной регрессии OLS позволяет предсказать значение переменной отклика для различных входных данных переменной предиктора с учетом коэффициентов наклона и пересечения линии наилучшего соответствия.
Линия наилучшего соответствия вычисляется в R с использованием функции lm(), которая выводит коэффициенты наклона и пересечения. Наклон и точка пересечения также могут быть рассчитаны по пяти сводным статистическим данным: стандартные отклонения x и y , средние значения x и y и коэффициент корреляции Пирсона между x и y переменными.
Наклон и точка пересечения также могут быть рассчитаны по пяти сводным статистическим данным: стандартные отклонения x и y , средние значения x и y и коэффициент корреляции Пирсона между x и y переменными.
наклон <- cor(x, y) * (sd(y) / sd(x)) intercept <- mean(y) - (slope * mean(x))
Диаграмма рассеяния — лучший способ оценить линейность между двумя числовыми переменными. По диаграмме рассеяния можно определить силу, направление и форму взаимосвязи. Чтобы выполнить линейную регрессию в R, нужны только данные, с которыми они работают, и базовые функции R lm() и predict(). В этом кратком руководстве используются два пакета, которые не являются частью базового R. Это 9 пакетов.0215 dplyr и ggplot2 .
Встроенный набор данных mtcars в R используется для визуализации двумерной зависимости между эффективностью использования топлива (миль на галлон) и рабочим объемом двигателя (disp).
библиотека (dplyr) библиотека (ggplot2) мткары %>% ggplot(aes(x = disp, y = mpg)) + geom_point (цвет = «красный»)
При визуальном осмотре зависимость кажется линейной, имеет отрицательное направление и выглядит умеренно сильной. Силу взаимосвязи можно количественно оценить с помощью коэффициента корреляции Пирсона.
cor(mtcars$disp, mtcars$миль на галлон) [1] -0,8475514
Это сильная отрицательная корреляция. Обратите внимание, что корреляция не подразумевает причинно-следственную связь . Он просто показывает, существует ли взаимная связь, причинная или нет, между переменными.
Если взаимосвязь нелинейна, общий подход к моделированию линейной регрессии заключается в преобразовании переменной-предиктора, чтобы сделать связь более линейной. Общие преобразования включают в себя натуральные и десятичные логарифмические, квадратный корень, кубический корень и обратные преобразования. Соотношение миль на галлон и расхода уже является линейным, но его можно усилить с помощью преобразования квадратного корня.
Соотношение миль на галлон и расхода уже является линейным, но его можно усилить с помощью преобразования квадратного корня.
мтвагонов %>% ggplot(aes(x = sqrt(disp), y = sqrt(миль на галлон))) + geom_point (цвет = «красный») cor(sqrt(mtcars$disp), sqrt(mtcars$миль на галлон)) [1] -0,8929046
Следующим шагом является определение того, является ли отношение статистически значимым , а не просто случайным явлением. Это делается путем исследования дисперсии точек данных на подобранной линии. Если данные хорошо подходят к линии, то связь, вероятно, будет реальным эффектом. Качество подгонки можно количественно оценить с помощью среднеквадратическая ошибка (RMSE) и R-квадрат метрики. RMSE представляет собой дисперсию ошибок модели и является абсолютной мерой соответствия, которая имеет единицы, идентичные переменной отклика. R -квадрат представляет собой просто квадрат коэффициента корреляции Пирсона и представляет дисперсию, объясненную в переменной отклика переменной-предиктором.
Количество точек данных также важно и влияет на p-значение модели. Эмпирическое правило для линейной регрессии OLS заключается в том, что для действительной модели требуется не менее 20 точек данных. Значение p — это вероятность отсутствия взаимосвязи (нулевая гипотеза) между переменными.
Линейная модель МНК теперь соответствует преобразованным данным.
мтвагонов %>% ggplot(aes(x = sqrt(disp), y = sqrt(миль на галлон))) + geom_point (цвет = "красный") + geom_smooth(method = "lm", fill = NA)
Объект модели можно создать следующим образом.
lmodel <- lm(sqrt(mpg) ~ sqrt(disp), data = mtcars)
Можно получить наклон и точку пересечения.
lmodel$коэффициенты (Перехват) sqrt(disp) 6,5192052 -0,1424601
И сводка модели содержит важную статистическую информацию.
сводка(lmodel) Вызов: lm (формула = sqrt (миль на галлон) ~ sqrt (disp), данные = mtcars) Остатки: Мин.1 кв. Медиана 3 кв. Макс. -0,45591 -0,21505 -0,07875 0,16790 0,71178 Коэффициенты: Оценка стд. Значение ошибки t Pr(>|t|) (Перехват) 6.51921 0,19921 32,73 < 2е-16*** sqrt(disp) -0,14246 0,01312 -10,86 6,44e-12 *** --- Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1 Остаточная стандартная ошибка: 0,3026 при 30 степенях свободы. Множественный R-квадрат: 0,7973, скорректированный R-квадрат: 0,7905 F-статистика: 118 на 1 и 30 DF, p-значение: 6,443e-12
-квадрат) 0,7973 дает объясненную дисперсию и может использоваться в качестве меры предсказательной силы (при отсутствии переобучения). Среднеквадратическая ошибка также включена в выходные данные (остаточная стандартная ошибка), где она имеет значение 0,3026.
Выводимое сообщение состоит в том, что на каждую единицу увеличения квадратного корня из рабочего объема двигателя уменьшается на -0,14246 квадратный корень топливной экономичности (миль на галлон). Таким образом, эффективность использования топлива снижается с увеличением объема двигателя.

 data.frame = T, use.missings = T)
data.frame = T, use.missings = T) 2 6 6 6.6 7 7.2 5.3 6.4 6.6 7.3 ...
## - attr(*, "variable.labels")= Named chr "age" "short-term memory span" "IQ" "reading ability"
## ..- attr(*, "names")= chr "AGE" "MEM_SPAN" "IQ" "READ_AB"
2 6 6 6.6 7 7.2 5.3 6.4 6.6 7.3 ...
## - attr(*, "variable.labels")= Named chr "age" "short-term memory span" "IQ" "reading ability"
## ..- attr(*, "names")= chr "AGE" "MEM_SPAN" "IQ" "READ_AB"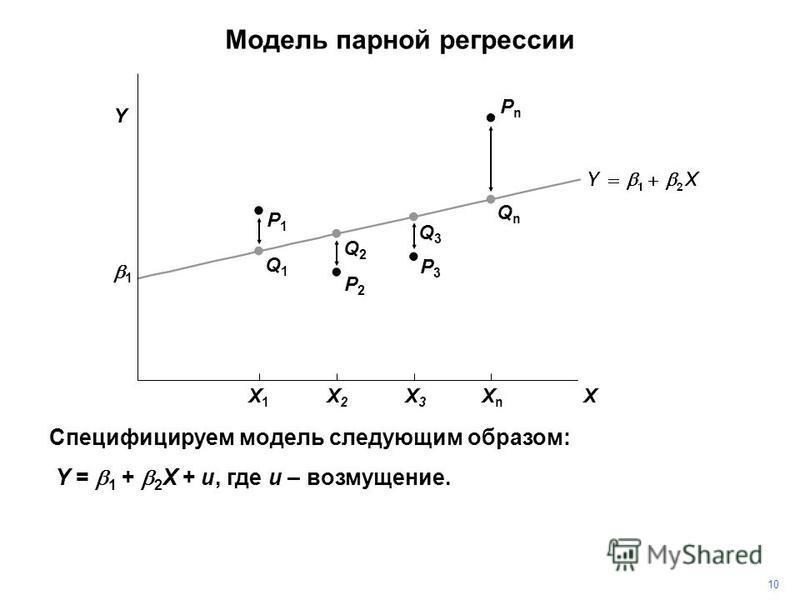 5 % 97.5 %
## (Intercept) 0.3439199 3.416711
## MEM_SPAN 0.6397881 1.313664
5 % 97.5 %
## (Intercept) 0.3439199 3.416711
## MEM_SPAN 0.6397881 1.313664 689546 5.982564 6.275582 6.763945 5.982564 7.252308
## 17 18 19 20
## 5.787219 5.982564 5.982564 5.787219
689546 5.982564 6.275582 6.763945 5.982564 7.252308
## 17 18 19 20
## 5.787219 5.982564 5.982564 5.787219 Error t value Pr(>|t|)
## (Intercept) 1.8803 0.7313 2.571 0.0192 *
## MEM_SPAN 0.9767 0.1604 6.090 9.37e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4037 on 18 degrees of freedom
## Multiple R-squared: 0.6733, Adjusted R-squared: 0.6551
## F-statistic: 37.09 on 1 and 18 DF, p-value: 9.374e-06
##
##
## ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
## USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
## Level of Significance = 0.05
##
## Call:
## gvlma(x = model)
##
## Value p-value Decision
## Global Stat 5.8582 0.2100 Assumptions acceptable.
## Skewness 1.0395 0.3079 Assumptions acceptable.
## Kurtosis 0.3692 0.5434 Assumptions acceptable.
## Link Function 2.0686 0.1504 Assumptions acceptable.
## Heteroscedasticity 2.3808 0.1228 Assumptions acceptable.
Error t value Pr(>|t|)
## (Intercept) 1.8803 0.7313 2.571 0.0192 *
## MEM_SPAN 0.9767 0.1604 6.090 9.37e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4037 on 18 degrees of freedom
## Multiple R-squared: 0.6733, Adjusted R-squared: 0.6551
## F-statistic: 37.09 on 1 and 18 DF, p-value: 9.374e-06
##
##
## ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
## USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
## Level of Significance = 0.05
##
## Call:
## gvlma(x = model)
##
## Value p-value Decision
## Global Stat 5.8582 0.2100 Assumptions acceptable.
## Skewness 1.0395 0.3079 Assumptions acceptable.
## Kurtosis 0.3692 0.5434 Assumptions acceptable.
## Link Function 2.0686 0.1504 Assumptions acceptable.
## Heteroscedasticity 2.3808 0.1228 Assumptions acceptable.
 914 \)
914 \)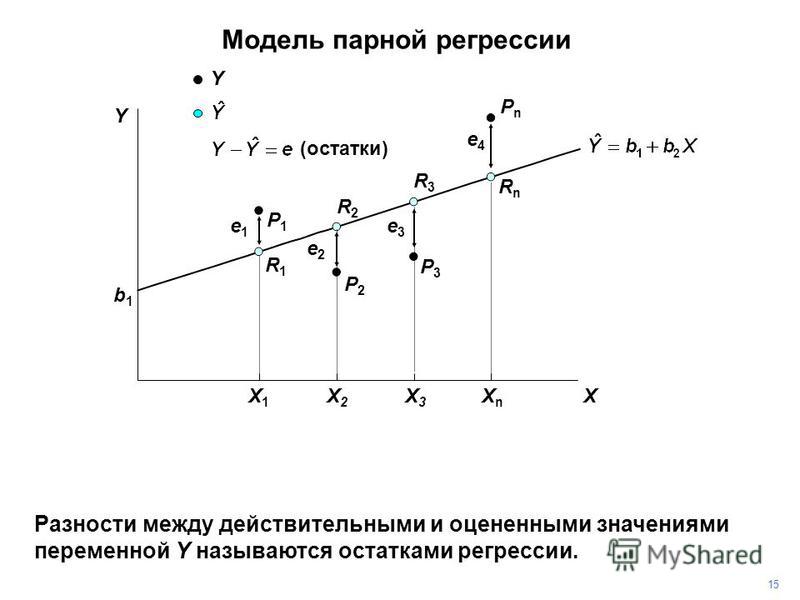 132 3.623 1.42 0.160
x1 1.160 0.664 1.75 0.084 .
x2 3.866 0.890 4.34 3.5e-05 ***
x1:x2 0.962 0.167 5.77 9.5e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 10.6 on 96 degrees of freedom
Multiple R-squared: 0.865, Adjusted R-squared: 0.861
F-statistic: 205 on 3 and 96 DF, p-value: <2e-16
132 3.623 1.42 0.160
x1 1.160 0.664 1.75 0.084 .
x2 3.866 0.890 4.34 3.5e-05 ***
x1:x2 0.962 0.167 5.77 9.5e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 10.6 on 96 degrees of freedom
Multiple R-squared: 0.865, Adjusted R-squared: 0.861
F-statistic: 205 on 3 and 96 DF, p-value: <2e-16
 2
2
 2
2
 2
2
 00% 3.57% 4.55%
100: 4.00% 3.57% 4.55%
150: 4.00% 3.57% 4.55%
200: 4.00% 3.57% 4.55%
250: 4.00% 3.57% 4.55%
300: 4.00% 3.57% 4.55%
350: 4.00% 3.57% 4.55%
400: 4.00% 3.57% 4.55%
450: 4.00% 3.57% 4.55%
500: 4.00% 3.57% 4.55%
00% 3.57% 4.55%
100: 4.00% 3.57% 4.55%
150: 4.00% 3.57% 4.55%
200: 4.00% 3.57% 4.55%
250: 4.00% 3.57% 4.55%
300: 4.00% 3.57% 4.55%
350: 4.00% 3.57% 4.55%
400: 4.00% 3.57% 4.55%
450: 4.00% 3.57% 4.55%
500: 4.00% 3.57% 4.55%
 rf.m2 <- predict(rf.m2, df[test.ids,])
rf.m2 <- predict(rf.m2, df[test.ids,])
 r-project.org/web/views/MachineLearning.html
r-project.org/web/views/MachineLearning.html

 А второй вид представляется неким черным ящиком, из которого чудесным образом извлекаются правильные значения. Из чего делается вывод, что все эти «математические изыскания» лишние, а нужно лишь найти на просторах интернета правильную процедуру и «прикрутить» её в проект, где она начинает выдавать значения «похожие на правильные». Подобный ситуативный путь решения проблемы разработчиком приводит к тому, что корректно проверить, модифицировать найденный код не представляется возможным и, соответственно, верифицировать получаемый результат тоже.
А второй вид представляется неким черным ящиком, из которого чудесным образом извлекаются правильные значения. Из чего делается вывод, что все эти «математические изыскания» лишние, а нужно лишь найти на просторах интернета правильную процедуру и «прикрутить» её в проект, где она начинает выдавать значения «похожие на правильные». Подобный ситуативный путь решения проблемы разработчиком приводит к тому, что корректно проверить, модифицировать найденный код не представляется возможным и, соответственно, верифицировать получаемый результат тоже.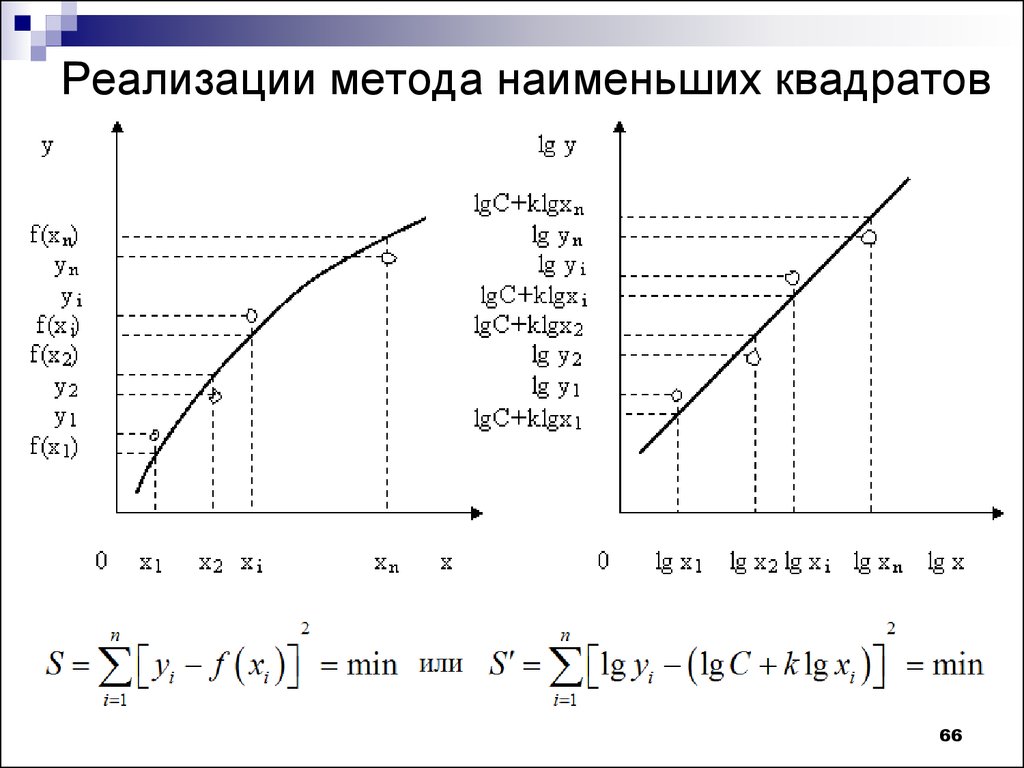 Таким образом, в представленной парадигме для детального объяснения МНК нужно:
Таким образом, в представленной парадигме для детального объяснения МНК нужно: Эти данные представим в виде таблицы, где строки – это объекты, первый столбец – набор параметров (j=1), второй столбец – набор измеренных ответов:
Эти данные представим в виде таблицы, где строки – это объекты, первый столбец – набор параметров (j=1), второй столбец – набор измеренных ответов: 2, 2.] # весовые коэффициенты
data_size = 200 # размер генерируемого набора данных
noise_sigma = 10 # СКО шума в данных
random_state = 42
x_scale, y_estimate = datasets_make_regression(coef_true, data_size, noise_sigma, random_state)
plt.plot(x_scale, y_estimate, 'o')
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)
2, 2.] # весовые коэффициенты
data_size = 200 # размер генерируемого набора данных
noise_sigma = 10 # СКО шума в данных
random_state = 42
x_scale, y_estimate = datasets_make_regression(coef_true, data_size, noise_sigma, random_state)
plt.plot(x_scale, y_estimate, 'o')
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14) Общее описание линейной модели.
Общее описание линейной модели.
 Последовательно сложность конечных выражений, используемых в алгоритмах, будет понижаться. Эти алгоритмы приведены для того, чтобы полученные выражения, можно было соотнести с классическими изданиями.
Последовательно сложность конечных выражений, используемых в алгоритмах, будет понижаться. Эти алгоритмы приведены для того, чтобы полученные выражения, можно было соотнести с классическими изданиями. Ниже приведен код реализующий этот алгоритм.
Ниже приведен код реализующий этот алгоритм.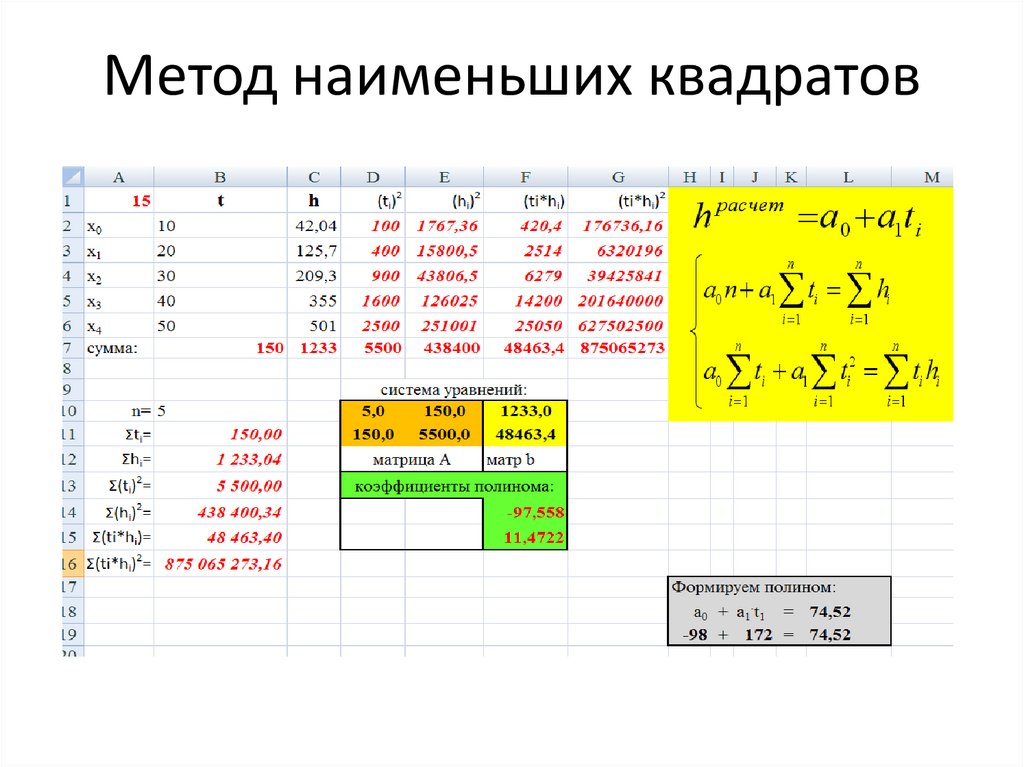 Пусть
Пусть 93193341] [2.01436546]
93193341] [2.01436546] 5
# оценка коэффициента корреляции величин x и y
corr_xy = (avg_xy - avg_x*avg_y)/(std_x*std_y)
# расчет искомых коэффициентов
w1 = corr_xy*std_y/std_x
w0 = avg_y - avg_x*w1
return w0, w1
[w0_3, w1_3] = coefficient_reg_stat(x_scale, y_estimate)
print(w0_3, w1_3)
5
# оценка коэффициента корреляции величин x и y
corr_xy = (avg_xy - avg_x*avg_y)/(std_x*std_y)
# расчет искомых коэффициентов
w1 = corr_xy*std_y/std_x
w0 = avg_y - avg_x*w1
return w0, w1
[w0_3, w1_3] = coefficient_reg_stat(x_scale, y_estimate)
print(w0_3, w1_3)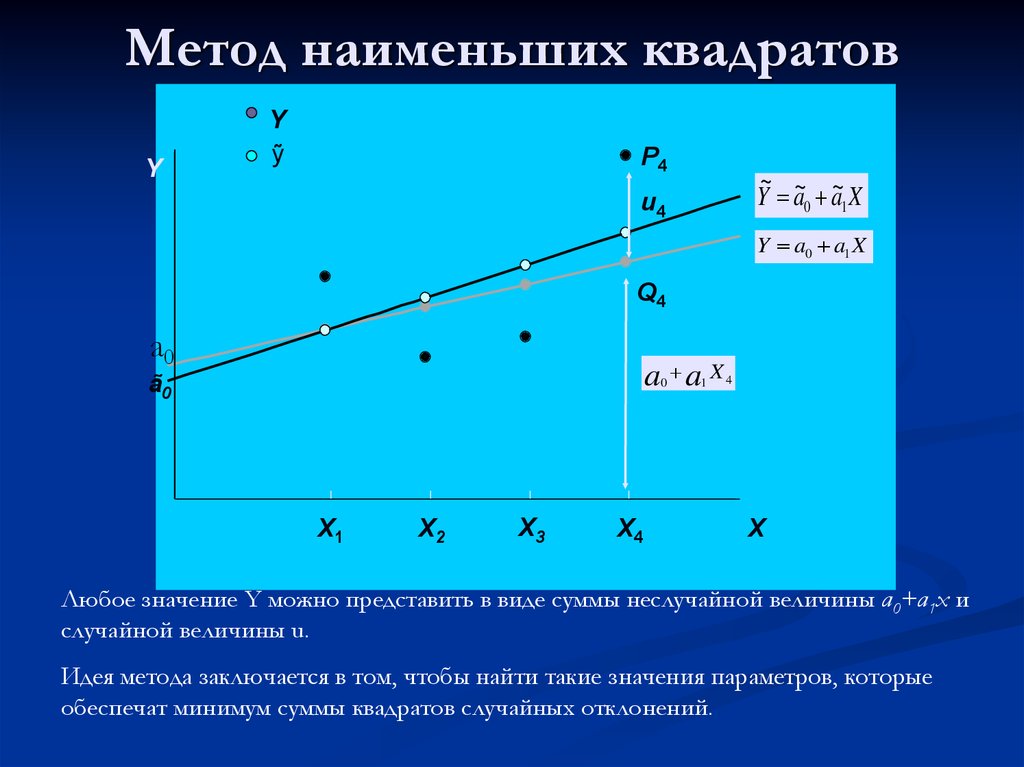
 При этом хочется отметить, что в алгоритмах (6) – (7) удалось уйти от процедуры обращения матрицы, которая при обработке реальных данных может выполняться нестабильно.
При этом хочется отметить, что в алгоритмах (6) – (7) удалось уйти от процедуры обращения матрицы, которая при обработке реальных данных может выполняться нестабильно.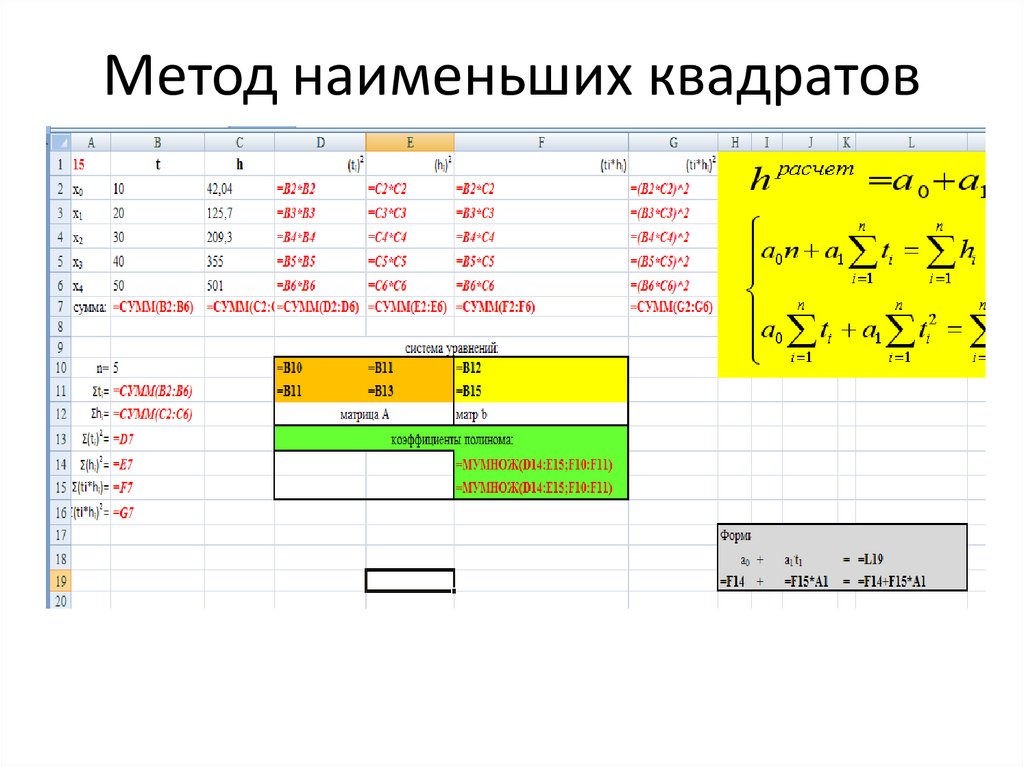 xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)
xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)  legend(loc = 'best', fontsize=12)
plt.xlim((30, 50))
plt.ylim((1.85, 2.15))
plt.xlabel('w0', fontsize=18)
plt.ylabel('w1', fontsize=18)
legend(loc = 'best', fontsize=12)
plt.xlim((30, 50))
plt.ylim((1.85, 2.15))
plt.xlabel('w0', fontsize=18)
plt.ylabel('w1', fontsize=18) Ray
кровати ←senic$Кровати
Ray
кровати ←senic$Кровати
 264806
264806
 05 '.' 0,1 '' 1
#>
#> Остаточная стандартная ошибка: 0,329 на 182 степенях свободы
#> Множественный R-квадрат: 0,754, скорректированный R-квадрат: 0,749
#> F-статистика: 139на 4 и 182 DF, p-значение: <2e-16
05 '.' 0,1 '' 1
#>
#> Остаточная стандартная ошибка: 0,329 на 182 степенях свободы
#> Множественный R-квадрат: 0,754, скорректированный R-квадрат: 0,749
#> F-статистика: 139на 4 и 182 DF, p-значение: <2e-16  1 кв. Медиана 3 кв. Макс.
-0,45591 -0,21505 -0,07875 0,16790 0,71178
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 6.51921 0,19921 32,73 < 2е-16***
sqrt(disp) -0,14246 0,01312 -10,86 6,44e-12 ***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 0,3026 при 30 степенях свободы.
Множественный R-квадрат: 0,7973, скорректированный R-квадрат: 0,7905
F-статистика: 118 на 1 и 30 DF, p-значение: 6,443e-12
1 кв. Медиана 3 кв. Макс.
-0,45591 -0,21505 -0,07875 0,16790 0,71178
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 6.51921 0,19921 32,73 < 2е-16***
sqrt(disp) -0,14246 0,01312 -10,86 6,44e-12 ***
---
Сигн. коды: 0 «***» 0,001 «**» 0,01 «*» 0,05 «.» 0,1 « » 1
Остаточная стандартная ошибка: 0,3026 при 30 степенях свободы.
Множественный R-квадрат: 0,7973, скорректированный R-квадрат: 0,7905
F-статистика: 118 на 1 и 30 DF, p-значение: 6,443e-12