1.3.4. Примеры решения задач по теме «Обратная матрица»
Задача 1.
Найти обратную матрицу для матрицы
И проверить выполнение условий А А-1 = А-1А = Е.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Убедимся, что матрица А – невырожденная. ΔА = 1·4 — 2·(-1) ≠ 0, следовательно, А-1 существует.
Вычислим алгебраические дополнения к элементам А:
Применим способ вычисления обратной матрицы:
.
Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам Транспонированной матрицы! |
Найдем произведения А А-1 и А-1А:
Таким образом, найденная матрица А-1 отвечает определению обратной матрицы.
Ответ: .
Задача 2.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Следовательно, матрица А невырожденная, и обратная матрица существует.
Вычислим алгебраические дополнения к элементам матрицы А:
Обратная матрица имеет вид:
Ответ: .
Задача 3.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Вычислим определитель матрицы А разложением по первому столбцу:
.
Следовательно, обратная матрица для матрицы А существует.
Найдем алгебраические дополнения к элементам матрицы А:
Значит,
.
Ответ: .
Задача 4.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
.
Ответ:
Задача 5.
При каких X, Y, Z матрица
Является обратной к матрице
Указание
Необходимым условием того, что В = А-1, является требование АВ = Е.
Решение
Проверим невырожденность матрицы А:
Необходимым условием того, что В = А-1, является требование АВ = Е.
Найдем АВ:
Для того, чтобы выполнялось условие
Проверим, будет ли равно единичной матрице произведение ВА:
Значит, при найденных значениях X, Y, Z В = А-1.
Ответ: X = -3, Y = -3, Z = 4.
| < Предыдущая | Следующая > |
|---|
Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту [email protected]
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
Как найти обратную матрицу 2х2 ?
Данное решение сделано калькулятором, представленным на сайте.
Найдем матрицу A-1, обратную исходной:
Запишем формулу для нахождения обратной матрицы:
| A-1 = 1 / det A * | A11 | A21 | |||
| A12 | A22 |
A11 … A22 — это числа (алгебраические дополнения), которые будут найдены позже.
На ноль делить нельзя. Поэтому если det A равен нулю, то найти обратную матрицу невозможно.
Поэтому если det A равен нулю, то найти обратную матрицу невозможно.
Вычислим det A.
= 1 * 3 — 1 * ( -1) = 3 + 1 = 4
det A не равен нулю. Следовательно, найти обратную матрицу возможно.
Вычислим числа (алгебраические дополнения) A
| Номер строки 1 Номер столбца 1 |
Строку 1 и столбец 1 вычеркнули |
|||||
| A11 | = | ( -1) 1 + 1 | * | 3 | = 3 |
| Номер строки 1 Номер столбца 2 |
Строку 1 и столбец 2 вычеркнули |
|||||
| A12 | = | ( -1) 1 + 2 | * | -1 | = 1 |
| Номер строки 2 Номер столбца 1 |
Строку 2 и столбец 1 вычеркнули |
|||||
| A21 | = | ( -1) 2 + 1 | * | 1 | = -1 |
| Номер строки 2 Номер столбца 2 |
Строку 2 и столбец 2 вычеркнули |
|||||
| A22 | = | ( -1) 2 + 2 | * | = 1 |
Ответ:
| A-1 = 1 / det A * | A11 | A21 | |||
| A12 | A22 |
Необходимо проверить, что выполняется условие: A-1 * A = E.
Мы будем использовать предпоследнюю форму записи обратной матрицы A-1.
Это позволит нам избежать вычислений с дробями.
b11 = 3 * 1 + ( -1) * ( -1) = 3 + 1 = 4
b12 = 3 * 1 + ( -1) * 3 = 3 — 3 = 0
b21 = 1 * 1 + 1 * ( -1) = 1 — 1 = 0
b22 = 1 * 1 + 1 * 3 = 1 + 3 = 4
Необходимо умножить получившуюся матрицу на 1/4
Таким образом, найденная матрица A-1 является обратной для исходной матрицы A.
| Алгебраические дополнения. | ∆ 1,2 = -(2·4-(-2·(-2))) = -4 | ∆ 2,1 = -(2·4-5·3) = 7 | ∆ 2,3 = -(-1·5-(-2·2)) = 1 | ∆ 3,2 = -(-1·(-2)-2·3) = 4 |
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .

Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Рассмотрим квадратную матрицу . Обозначим Δ = det A ее определитель. Квадратная В есть (ОМ) для квадратной А того же порядка, если их произведение А*В = В* А = Е, где Е — единичная матрица того же порядка, что и А и В.
Квадратная А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0.
Теорема. Для того, чтобы А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
(ОМ) А, обозначается через А -1 , так что В = А -1 и вычисляется по формуле
, (1)
где А i j — алгебраические дополнения элементов a i j , Δ = detA.
Вычисление A -1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A -1 с помощью метода элементарных преобразований (ЭП). Любую неособенную А путем ЭП только столбцов (или только строк) можно привести к единичной Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной Е, то в результате получится A -1 . Удобно совершать ЭП над А и Е одновременно, записывая обе рядом через черту A|E. Если нужно найти A -1 , в процессе преобразований следует использовать только строки или только столбцы.
Если совершенные над матрицей А ЭП в том же порядке применить к единичной Е, то в результате получится A -1 . Удобно совершать ЭП над А и Е одновременно, записывая обе рядом через черту A|E. Если нужно найти A -1 , в процессе преобразований следует использовать только строки или только столбцы.
Нахождение обратной матрицы с помощью алгебраических дополнений
Пример 1 . Для найти A -1 .
Решение. Находим сначала детерминант А
значит, (ОМ) существует и мы ее можем найти по формуле: , где А i j (i,j=1,2,3) — алгебраические дополнения элементов а i j исходной А.
Алгебраическое дополнение элемента a ij это определитель или минор M ij . Он получается вычеркиванием столбца i и строки j. Затем минор умножается на (-1) i+j , т.е. A ij =(-1) i+j M ij
откуда .
Нахождение обратной матрицы с помощью элементарных преобразований
Пример 2 . Методом элементарных преобразований найти A -1 для: А= .
Решение. Приписываем к исходной A справа единичную того же порядка: . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой «половиной».
Для этого поменяем местами первый и второй столбцы: ~. К третьему столбцу прибавим первый, а ко второму — первый, умноженный на -2: . Из первого столбца вычтем удвоенный второй, а из третьего — умноженный на 6 второй; . Прибавим третий столбец к первому и второму: . Умножим последний столбец на -1: . Полученная справа от вертикальной черты квадратная таблица является обратной А -1 . Итак,
.
Пусть имеется квадратная матрица n-го порядка
Матрица А -1 называется обратной матрицей по отношению к матрице А, если А*А -1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица может существовать только для квадратных матриц т. е. для тех матриц, у которых число строк и столбцов совпадают.
е. для тех матриц, у которых число строк и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…А n) называется невырожденной , если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
Алгоритм нахождения обратной матрицы
- Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
- Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
- Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.

- Записать обратную матрицу А -1 , которая находится в последней таблице под матрицей Е исходной таблицы.
Для матрицы А найти обратную матрицу А -1
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А -1 .
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:
Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.
Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
Пример 2Решить уравнение АХ = В, если
Решение : Так как обратная матрица равняется (см. пример 1)
Матричный метод в экономическом анализе
Наряду с другими в находят применение также матричные методы . Эти методы базируются на линейной и векторно-матричной алгебре. Такие методы применяются для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений.
В процессе применения матричных методов анализа можно выделить несколько этапов.
На первом этапе осуществляется формирование системы экономических показателей и на ее основе составляется матрица исходных данных , которая представляет собой таблицу, в которой по ее отдельным строкам показываются номера систем (i = 1,2,….,n) , а по вертикальным графам — номера показателей (j = 1,2,. …,m) .
…,m) .
На втором этапе по каждой вертикальной графе выявляется наибольшее из имеющихся значений показателей, которое и принимается за единицу.
После этого все суммы, отраженные в данной графе делят на наибольшее значение и формируется матрица стандартизированных коэффициентов .
На третьем этапе все составные части матрицы возводят в квадрат. Если они имеют различную значимость, то каждому показателю матрицы присваивается определенный весовой коэффициент k . Величина последнего определяется экспертным путем.
На последнем, четвертом этапе найденные величины рейтинговых оценок R j группируются в порядке их увеличения или уменьшения.
Изложенные матричные методы следует использовать, например, при сравнительном анализе различных инвестиционных проектов, а также при оценке других экономических показателей деятельности организаций.
три алгоритма и примеры. Решение матричных уравнений
Определение 1: матрица называется вырожденной, если её определитель равен нулю.
Определение 2: матрица называется невырожденной, если её определитель не равен нулю.
Матрица «A» называется обратной матрицей , если выполняется условие A*A-1 = A-1 *A = E (единичной матрице).
Квадратная матрица обратима только в том случае, когда она является невырожденной.
Схема вычисления обратной матрицы:
1) Вычислить определитель матрицы «A», если ∆ A = 0, то обратной матрицы не существует.
2) Найти все алгебраические дополнения матрицы «A».
3) Составить матрицу из алгебраических дополнений (Aij )
4) Транспонировать матрицу из алгебраических дополнений (Aij )T
5) Умножить транспонированную матрицу на число, обратное определителю данной матрицы.
6) Выполнить проверку:
На первый взгляд может показаться, что это сложно, но на самом деле всё очень просто. Все решения основаны на простых арифметических действиях, главное при решении не путаться со знаками «-» и «+», и не терять их.
А теперь давайте вместе с Вами решим практическое задание, вычислив обратную матрицу.
Задание: найти обратную матрицу «A», представленную на картинке ниже:
Решаем всё в точности так, как это указано в план-схеме вычисления обратной матрицы.1. Первое, что нужно сделать, это найти определитель матрицы «A»:
Пояснение:
Мы упростили наш определитель, воспользовавшись его основными функциями. Во первых, мы прибавили ко 2 и 3 строке элементы первой строки, умноженные на одно число.
Во-вторых, мы поменяли 2 и 3 столбец определителя, и по его свойствам поменяли знак перед ним.
В-третьих, мы вынесли общий множитель (-1) второй строки, тем самым, снова поменяв знак, и он стал положительным. Также мы упростили 3 строку также, как в самом начале примера.
У нас получилась треугольный определитель, у которого элементы ниже диагонали равны нулю, и по 7 свойству он равен произведению элементов диагонали. В итоге мы получили ∆ A = 26, следовательно обратная матрица существует.
А11 = 1*(3+1) = 4
А12 = -1*(9+2) = -11
А13 = 1*1 = 1
А21 = -1*(-6) = 6
А22 = 1*(3-0) = 3
А23 = -1*(1+4) = -5
А31 = 1*2 = 2
А32 = -1*(-1) = -1
А33 = 1+(1+6) = 7
3. Следующий шаг — составление матрицы из получившихся дополнений:
5. Умножаем эту матрицу на число, обратное определителю, то есть на 1/26:
6. Ну а теперь нам просто нужно выполнить проверку:
В ходе проверки мы получили единичную матрицу, следовательно, решение было выполнено абсолютно верно.
2 способ вычисления обратной матрицы.
1. Элементарное преобразование матриц
2. Обратная матрица через элементарный преобразователь.
Элементарное преобразование матриц включает:
1. Умножение строки на число, не равное нулю.
2. Прибавление к любой строке другой строки, умноженной на число.
3. Перемена местами строк матрицы.
4. Применяя цепочку элементарных преобразований, получаем другую матрицу.
А-1 = ?
1. (A|E) ~ (E|A-1 )
2. A-1 * A = E
Рассмотрим это на практическом примере с действительными числами.
Задание: Найти обратную матрицу.
Решение:
Выполним проверку:
Небольшое разъяснение по решению:
Сперва мы переставили 1 и 2 строку матрицы, затем умножили первую строку на (-1).
После этого умножили первую строку на (-2) и сложили со второй строкой матрицы. После чего умножили 2 строку на 1/4.
Заключительным этапом преобразований стало умножение второй строки на 2 и прибавлением с первой. В результате слева у нас получилась единичная матрица, следовательно, обратная матрица — это матрица справа.
После проверки мы убедились в правильности решения.
Как вы видите, вычисление обратной матрицы — это очень просто.
В заключении данной лекции хотелось бы также уделить немного времени свойствам такой матрицы.
Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…
Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…
Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.
На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?
…да, такое бывает только по любви =)
Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Ну, и совсем замечательно, если отработано понижение порядка определителя .
Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований .
Не мудрствуя лукаво:
Пример 1
Решить систему методом Гаусса-Жордана
Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:
Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .
Идеальный с точки зрения простоты случай:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) К первой строке прибавили вторую строку, умноженную на –2.
Не могу удержаться от иллюстрации итоговой системы:
Ответ :
Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.
Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:
Пример 2
Решить систему линейных уравнений методом Гаусса-Жордана.
Решение : первая часть задания хорошо знакома:
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.
(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.
(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7
(4) Третью строку разделили на 2.
Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .
Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:
Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т. е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:
е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:
(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.
(8) К первой строке прибавили вторую.
(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!
В результате элементарных преобразований получена эквивалентная исходной система:
Элементарно выражаем базисные переменные через свободную:
и записываем:
Ответ : общее решение:
В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.
И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .
Для самостоятельного решения:
Пример 3
Найти базисное решение с помощью элементарных преобразований
Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.
Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.
Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.
Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь ни при чём!
Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .
Продолжаем совершенствовать свои навыки на следующей прикладной задаче:
Как найти обратную матрицу методом Гаусса?Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.
Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:
(Понятно, что обратная матрица должна существовать)
Демо-пример 4
Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:
(1) Ко второй строке прибавили первую строку, умноженную на –3.
(2) К первой строке прибавили вторую строку.
(3) Вторую строку разделили на –2.
Ответ :
Сверьтесь с ответом первого примера урока Как найти обратную матрицу?
Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:
Как правило, вам будет предложена матрица «три на три»:
Пример 5
Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :
(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.
(3) К 3-й строке прибавили 2-ю строку, умноженную на –1
Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.
Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.
К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.
(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:
(5) К 1-й и 2-й строкам прибавили третью строку.
(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.
(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.
(8) К первой строке прибавили вторую строку.
(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.
(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.
Совершенно понятно, что это число 44. Третью строку умножаем на 11.
(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!
Таким образом, обратная матрица:
Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.
Ответ :
Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .
Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.
Аналогичное задание для самостоятельного решения:
Пример 6
Найти обратную матрицу методом Гаусса-Жордана.
Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .
Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .
На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».
И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .
Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:
Пример 7
Найти обратную матрицу с помощью элементарных преобразований
Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.
Моя поздняя версия внизу страницы.
И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)
Желаю успехов!
Решения и ответы:
Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:
(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :
Ответ : общее решение:
Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:
(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.
(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :
Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:
(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :
Обратная матрица для данной это такая матрица, умножение исходной на которую дает единичную матрицу: Обязательным и достаточным условием наличия обратной матрицы является неравенство нулю детерминанта исходной (что в свою очередь подразумевает, что матрица должна быть квадратная).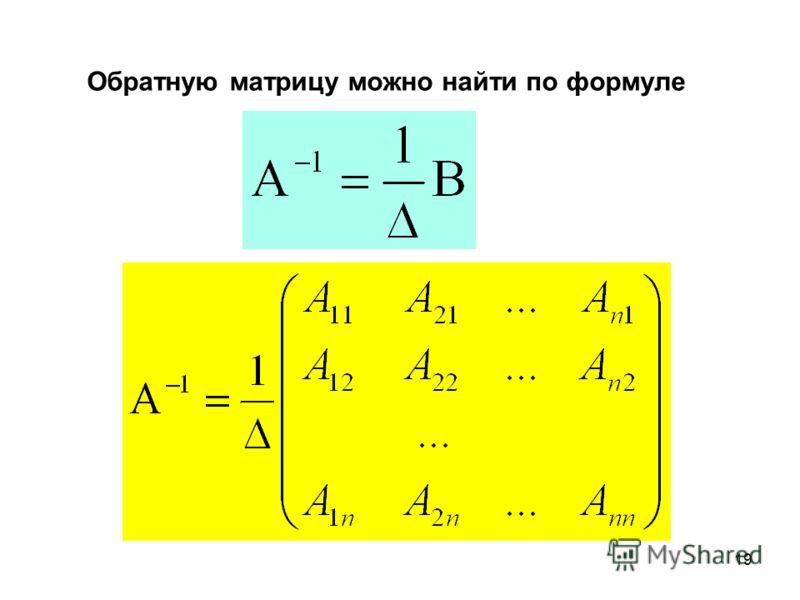 Если же определитель матрицы равняется нулю, то ее называют вырожденной и такая матрица не имеет обратной. В высшей математике обратные матрицы имеют важное значение и применяются для решения ряда задач. Например, на нахождении обратной матрицы построен матричный метод решения систем уравнений. Наш сервис сайт позволяет вычислять обратную матрицу онлайн двумя методами: методом Гаусса-Жордана и с помощью матрицы алгебраических дополнений. Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн
Если же определитель матрицы равняется нулю, то ее называют вырожденной и такая матрица не имеет обратной. В высшей математике обратные матрицы имеют важное значение и применяются для решения ряда задач. Например, на нахождении обратной матрицы построен матричный метод решения систем уравнений. Наш сервис сайт позволяет вычислять обратную матрицу онлайн двумя методами: методом Гаусса-Жордана и с помощью матрицы алгебраических дополнений. Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн
Найти обратную матрицу на сайт
сайт позволяет находить обратную матрицу онлайн быстро и бесплатно. На сайте произвордятся вычисления нашим сервисом и выдается результат с подробным решением по нахождению обратной матрицы . Сервер всегда выдает только точный и верный ответ. В задачах по определению обратной матрицы онлайн , необходимо, чтобы определитель матрицы был отличным от нуля, иначе сайт сообщит о невозможности найти обратную матрицу ввиду равенства нулю определителя исходной матрицы. Задача по нахождению обратной матрицы встречается во многих разделах математики, являясь одним из самых базовых понятий алгебры и математическим инструментом в прикладных задачах. Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ.
Сервер всегда выдает только точный и верный ответ. В задачах по определению обратной матрицы онлайн , необходимо, чтобы определитель матрицы был отличным от нуля, иначе сайт сообщит о невозможности найти обратную матрицу ввиду равенства нулю определителя исходной матрицы. Задача по нахождению обратной матрицы встречается во многих разделах математики, являясь одним из самых базовых понятий алгебры и математическим инструментом в прикладных задачах. Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.
Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.
Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a , не равного нулю, существует такое число b , что произведение a и b равно единице: ab = 1 . Число b называется обратным для числа b . Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.
Обратной матрицей , которую требуется отыскать для данной квадратной матрицы А , называется такая матрица
произведение на которую матрицы А справа является единичной матрицей, т.е,
. (1)
Единичной матрицей называется диагональная матрица, у которой все диагональные
элементы равны единице.
Нахождение обратной матрицы — задача, которая чаще решается двумя методами:
- методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).
Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной , несингулярной ), если её определитель не равен нулю, и особенной (или вырожденной , сингулярной ), если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
Нахождение обратной матрицы методом исключения неизвестных Гаусса
Первый шаг для нахождения обратной матрицы методом исключения неизвестных Гаусса — приписать к матрице A единичную матрицу того же порядка, отделив их вертикальной чертой. Мы получим сдвоенную матрицу . Умножим обе части этой матрицы на , тогда получим
,
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась
единичная матрица, тогда в правой части на месте
единичной матрицы автоматически получится обратная матрица. Матрица A в левой части
преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы
найти обратную матрицу.
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её
с третьей строкой. Тогда получим
Тогда получим
.
Разделим третью строку на 8, тогда
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
.
Переставим местами вторую и третью строку, тогда окончательно получим:
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица . Таким образом:
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
В результате должна получиться обратная матрица.
онлайн калькулятора для нахождения обратной матрицы .
Пример 3. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим
.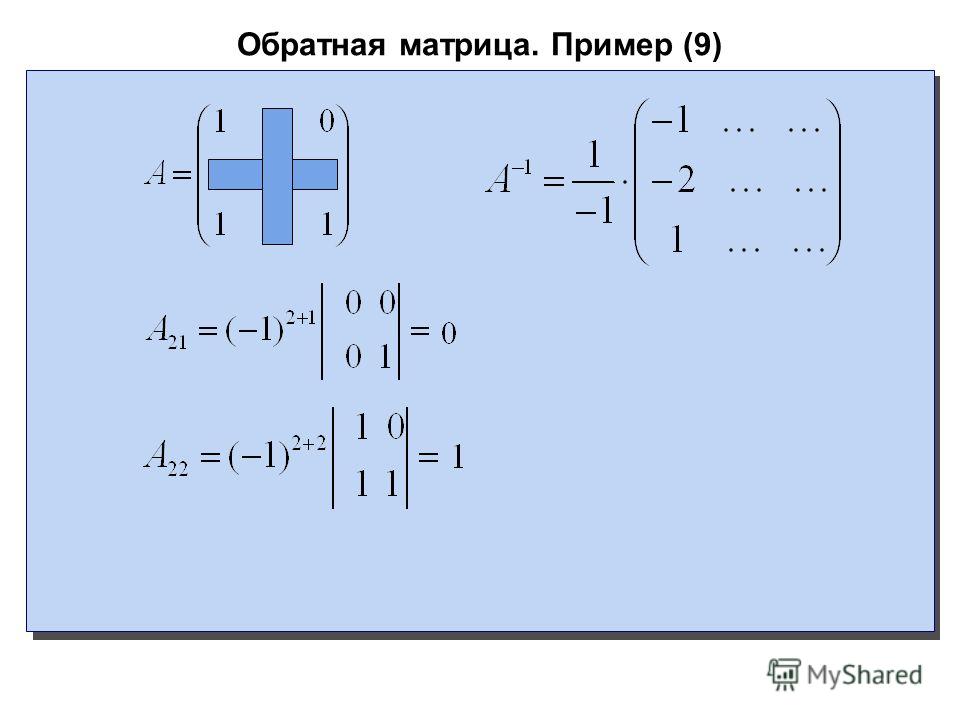
Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Проверить решение можно с помощью
Способы нахождения обратной матрицы. Рассмотрим квадратную матрицу
Обозначим Δ = det A.
Квадратная матрица А называется невырожденной, или неособенной , если ее определитель отличен от нуля, и вырожденной, или особенной , если Δ = 0.
Квадратная матрица В есть для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е — единичная матрица того же порядка, что и матрицы А и В.
Теорема . Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Обратная матрица матрице А, обозначается через А — 1 , так что В = А — 1 и вычисляется по формуле
, (1)
где А i j — алгебраические дополнения элементов a i j матрицы A. .
.
Вычисление A -1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A -1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример 1 . Для матрицы найти A -1 .
Решение. Находим сначала детерминант матрицы А
значит, обратная матрица существует и мы ее можем найти по формуле: , где А i j (i,j=1,2,3) — алгебраические дополнения элементов а i j исходной матрицы.
Откуда .
Пример 2 . Методом элементарных преобразований найти A -1 для матрицы: А= .
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы: ~
. К третьему столбцу прибавим первый, а ко второму — первый, умноженный на -2: . Из первого столбца вычтем удвоенный второй, а из третьего — умноженный на 6 второй; . Прибавим третий столбец к первому и второму: . Умножим последний столбец на -1: . Полученная справа от вертикальной черты квадратная матрица является обратной матрицей к данной матрице А. Итак,
.
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Олег Шпинарев (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2),
Нахождение обратной матрицы с примерами решения
Содержание:
- Примеры с решением
- Пример 8.
 1.
1. - Пример 8.2.
Определение 8.1. Пусть — квадратная матрица порядка . Квадратную матрицу того же порядка называют обратной к , если , где — единичная матрица порядка .
Обратную матрицу обозначают . Она позволяет определить целую отрицательную степень матрицы . А именно, для полагают .
Теорема 8.1. Если квадратная матрица имеет обратную матрицу, то обратная матрица единственная.
Предположим, что матрица имеет две обратные матрицы и . Тогда, согласно определению 8.1 обратной матрицы, выполнены, в частности, равенства . Используя ассоциативность умножения матриц, получаем , т.е. матрицы В и В’ совпадают.
| Квадратная матрица не всегда имеет обратную. |
Установить, имеет ли данная матрица обратную, позволяет следующий критерий.
Теорема 8.2. Для того чтобы квадратная матрица порядка имела обратную, необходимо и достаточно, чтобы .
Необходимость. Пусть — матрица, обратная к . Тогда , но, согласно свойству 7.11 определителей, . Поэтому и, следовательно, . Достаточность. Пусть . Рассмотрим алгебраическое дополнение матрицы , соответствующее элементу ( — минор этого же элемента).
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Согласно свойству 7.7 определителей, для любого выполнены равенства (7.4) . Согласно свойству 7.9 определителей, для любых индексов выполнены равенства (7.8) . Рассмотрим теперь квадратную матрицу порядка с элементами
.
Матрица имеет элементы т.е. — это единичная матрица. Аналогично матрица имеет элементы следовательно, матрица является единичной. Согласно определению 8.1, матрица является обратной для .
Следствие 8.1. Если квадратная матрица имеет обратную, то . Действительно, .
Квадратную матрицу с ненулевым определителем называют невырожденной или неособой. |
В противном случае, когда определитель матрицы равен нулю, ее называют вырожденной. Итак, для существования обратной матрицы необходимо и достаточно, чтобы сама матрица была невырожденной.
Теорема 8.3. Если квадратные матрицы и порядка имеют обратные матрицы, то и их произведение имеет обратную матрицу, причем . В соответствии с определением 8.1 обратной матрицы достаточно доказать два равенства: . Используя ассоциативность умножения матриц (см. 6.4), получаем что и требовалось доказать.
Возможно вам будут полезны данные страницы:
Теорема 8.4. Если матрица порядка имеет обратную, то и транспонированная матрица имеет обратную, причем . Нужно убедиться, что и . Используя свойство произведения матриц относительно операции транспонирования, имеем
Вычисление обратной матрицы
Применяют два основных метода вычисления обратной матрицы. Первый вытекает из теоремы 8. 2 и состоит в следующем. Пусть дана квадратная матрица порядка . Матрицу , транспонированную к матрице алгебраических дополнений, называют присоединенной. Как следует из доказательства теоремы 8.2, если — невырожденная матрица, то обратная к ней имеет вид . Таким образом, чтобы для квадратной матрицы порядка найти обратную матрицу, надо вычислить один определитель порядка и составить присоединенную матрицу, т.е. вычислить определителей порядка .
2 и состоит в следующем. Пусть дана квадратная матрица порядка . Матрицу , транспонированную к матрице алгебраических дополнений, называют присоединенной. Как следует из доказательства теоремы 8.2, если — невырожденная матрица, то обратная к ней имеет вид . Таким образом, чтобы для квадратной матрицы порядка найти обратную матрицу, надо вычислить один определитель порядка и составить присоединенную матрицу, т.е. вычислить определителей порядка .
Метод присоединенной матрицы эффективен при или , но при росте становится слишком трудоемким.
Примеры с решением
Пример 8.1.
Выясним, имеет ли матрица
обратную и если имеет, то найдем ее. Поскольку , матрица является невырожденной и, согласно теореме 8.2, имеет обратную. Для ее вычисления последовательно находим
Отметим, что для квадратной матрицы второго порядка присоединенная матрица получается перестановкой в диагональных элементов и изменением знака двух других.
Проверка ответа выполняется в соответствии с определением 8.1 обратной матрицы:
Второй метод вычисления обратной матрицы состоит в преобразовании исходной матрицы к более простому виду с помощью элементарных преобразований строк.
Чтобы найти матрицу , обратную к , фактически надо решить матричное уравнение . Отметим, что если над матрицей выполняется какое-либо элементарное преобразование строк, то это же преобразование осуществляется и над матрицей , поскольку любое элементарное преобразование строк матрицы эквивалентно умножению ее слева на соответствующую матрицу специального вида.
Таким образом, если в уравнении над матрицами и одновременно выполнить какое-либо элементарное преобразование строк, т.е. домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное уравнение .
Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное преобразование строк имеет обратное элементарное преобразование строк. Последовательность элементарных преобразований строк надо подобрать так, чтобы на -м шаге матрица превратилась в единичную матрицу. В результате этих шагов получается уравнение , где , т.е. . Итак, поскольку является решением уравнения , которое эквивалентно , то .
Последовательность элементарных преобразований строк надо подобрать так, чтобы на -м шаге матрица превратилась в единичную матрицу. В результате этих шагов получается уравнение , где , т.е. . Итак, поскольку является решением уравнения , которое эквивалентно , то .
Чтобы синхронно выполнять преобразования над матрицами в левой и правой частях матричного уравнения , записывают блочную матрицу и выполняют такие элементарные преобразования строк этой матрицы, чтобы вместо получить единичную матрицу .
Пример 8.2.
Продемонстрируем изложенный метод нахождения обратной матрицы для матрицы из примера 8.1. Для этого записываем матрицу и выполняем элементарные преобразования ее строк в следующем порядке: Таким образом,
.
Инверсия матрицы 2×2
В этом уроке мы будем иметь дело только с квадратными матрицами 2 × 2 . Я подготовил пять (5) рабочих примеров, чтобы проиллюстрировать процедуру решения или нахождения обратной матрицы с использованием метода формул .
Чтобы дать вам общее представление, две матрицы обратны друг другу, если их произведение представляет собой единичную матрицу . Единичная матрица размером 2 × 2 — это матрица с нулями всюду, но с единицей на диагонали.Это выглядит так.
Важно знать, как матрица и обратная ей связаны результатом их произведения. Итак,
- Если матрица A 2 × 2 является обратимой и умножается на ее обратную (обозначается символом A −1 ), в результате получается матрица идентичности, обозначаемая I. Чтобы проиллюстрировать эту концепцию, см. диаграмму ниже.
- Фактически, я могу переключать порядок или направление умножения между матрицами A и A −1 , и я все равно получу матрицу идентичности I.Это означает, что обратимые матрицы коммутативны.
Как найти обратную матрицу? Формула довольно проста. Пока вы следуете ему, проблем быть не должно. Вот так.
Формула для нахождения обратной матрицы 2 × 2
Учитывая матрицу A
Обратное значение рассчитывается по формуле
, где \ color {red} {\ rm {det}} \, A читается как определитель матрицы A.
Несколько замечаний по поводу формулы:
- Записи \ color {blue} a и \ color {blue} d из матрицы A меняются местами с точки зрения позиции в формуле.
- Записи \ color {blue} b и \ color {blue} c из матрицы A остаются на своих текущих позициях, однако их знаки меняются местами. Другими словами, ставьте отрицательные символы перед записями b и c.
- Поскольку \ color {red} {\ rm {det}} \, A — это просто число, то \ large {1 \ over {{\ rm {det}} A}} также является числом, которое будет служить скалярный множитель к матрице
См. Мой отдельный урок по скалярному умножению матриц.
Примеры того, как найти обратную матрицу 2 × 2
Пример 1: Найдите обратную матрицу 2 × 2 ниже, если она существует.
Формула требует от нас найти определитель данной матрицы. Ты помнишь, как это делать? Если нет, ничего страшного. Просмотрите приведенную ниже формулу, как найти определитель матрицы 2 × 2.
Итак, определитель матрицы A равен
Чтобы найти обратное, мне просто нужно подставить значение {\ rm {det}} A = — 1 в формулу, выполнить некоторую «реорганизацию» записей и, наконец, выполнить скалярное умножение.
- Вот снова формула для нахождения обратной матрицы 2 × 2.
- Теперь найдем обратную матрицу A.
Давайте затем проверим, правильна ли наша обратная матрица, выполнив матричное умножение A и A -1 двумя способами, и посмотрим, получаем ли мы матрицу идентичности.
Так как умножение обоих способов генерирует матрицу идентичности, то мы гарантируем, что обратная матрица, полученная с помощью формулы, является правильным ответом!
Пример 2: Найдите обратную матрицу 2 × 2 ниже, если она существует.
Сначала найдите определитель матрицы B.
Во-вторых, подставьте в формулу значение det B = 1 , а затем реорганизуйте элементы матрицы B, чтобы они соответствовали формуле.
Я предоставлю вам проверить, что
Другими словами, матричное произведение B и B -1 в любом направлении дает матрицу идентичности.
Пример 3: Найдите матрицу, обратную матрице ниже, если она существует.
Это отличный пример, потому что определитель не равен ни +1, ни -1, что обычно приводит к обратной матрице, имеющей рациональные или дробные элементы. Я должен признать, что большинство задач, поставленных учителями ученикам об обратной матрице 2 × 2, аналогичны этой.
Шаг 1 : Найдите определитель матрицы C.
- Формула для определения определителя
- Ниже представлено анимированное решение для вычисления определителя матрицы C
Шаг 2 : Определитель матрицы C равен −2.Подставьте значение в формулу, затем упростите, чтобы получить обратную матрицу C.
Шаг 3 : Проверьте правильность вычисленной обратной матрицы, выполнив умножение левой и правой матриц для получения матрицы идентичности.
Да, матричное умножение работает в обоих случаях, как показано ниже.
Первый случай:
Второй корпус:
Пример 4: Найдите матрицу, обратную матрице ниже, если она существует.
В наших предыдущих трех примерах нам удалось найти инверсию заданных 2 \ умноженных на 2 матриц.Я не хочу, чтобы у вас сложилось впечатление, что все матрицы 2 \ 2 имеют обратные.
В этом примере я хочу проиллюстрировать, когда данная матрица 2 \ умноженная на 2 не имеет инверсии. Как это случилось?
Если мы еще раз рассмотрим формулу, очевидно, что такая ситуация может возникнуть, когда определитель данной матрицы равен нулю , потому что 1, деленное на ноль, не определено . Итак, неопределенный член, распределенный по каждой записи матрицы, не имеет никакого смысла.
Вернемся к задаче определения определителя матрицы D.
Следовательно, , обратная матрице D, не существует , потому что определитель D равен нулю. Это наш окончательный ответ!
Пример 5: Найдите матрицу, обратную матрице ниже, если она существует.
Шаг 1 : Найдите определитель матрицы E.
Шаг 2 : Реорганизуйте элементы матрицы E, чтобы они соответствовали формуле, и замените решенное значение определителя матрицы E.Распределите значение \ large {1 \ over {{\ rm {det}} E}} по элементам матрицы E, затем упростите, если возможно.
Шаг 3 : Проверьте свой ответ, убедившись, что вы получили матрицу идентичности в обоих сценариях.
Первый сценарий:
Второй сценарий:
Практика с рабочими листами
Возможно, вас заинтересует:
Функция, обратная абсолютному значению
Функция, обратная постоянной
Обратная экспоненциальная функция
Функция, обратная линейной
Обратная логарифмическая функция
Обратная квадратичная функция
Обратная рациональная функция
Функция, обратная квадратному корню
5.
 Нахождение обратной матрицы
Нахождение обратной матрицыМ. Борна
Что мы делаем?
Если мы умножим матрицу A на , инверсный матрицы A , мы получим идентичную матрицу , I .
Концепция решения систем с использованием матриц аналогична концепции решения простых уравнений.
Например, чтобы решить 7 x = 14, мы умножаем обе стороны на одно и то же число. Мы находим «обратное» к «7», то есть «1/7».Умножение обеих частей слева на `1/7` дает:
`(1/7) × 7x = (1/7) × 14`
На слева имеем (частично):
`(1/7) × 7 = 1`
Число «1» — это «тождество» для умножения обычных чисел. На правом получаем:
`1/7 хх 14 = 2`.
Решение нашего уравнения:
х = 2
Мы расширяем эту концепцию поиска обратного решения одного уравнения до решения систем одновременных уравнений.
Нам нужно найти обратные матрицы, чтобы мы могли решать системы одновременных уравнений.
(Мы увидим, как решать системы в следующем разделе, Матрицы и линейные уравнения).
Мы найдем обратную матрицу, используя 2 разных метода. Вы можете решить, какой из них использовать, в зависимости от ситуации.
Первый метод ограничен нахождением обратной матрицы 2 × 2. Он включает использование определителя матрицы, которую мы видели ранее.
Напоминание: Мы можем найти только определитель квадратной матрицы . Например, если A — квадратная матрица
`((2,3), (- 1,5))`
, то мы можем найти определитель из A :
`| (2,3), (- 1,5) | = 10 + 3 = 13`
Для удобства мы могли бы записать определитель матрицы `A` как` | A | `, и поэтому наш окончательный ответ будет:
`| A | = 13`
Другой способ записать то же самое — использовать «det» для «определителя». -1 = 1 / | A | ((- 7,3), (- 4,2))`
-1 = 1 / | A | ((- 7,3), (- 4,2))`
`= 1 / (- 2) ((- 7,3), (- 4,2))`
`= ((3.-1A = ((3,5, -1,5), (2, -1)) ((2, -3), (4, -7)) `
`= ((7-6, -10,5 + 10,5), (4-4, -6 + 7))`
`= ((1,0), (0,1))`
`= I`
Мы можем лечь спать счастливыми, зная, что наш ответ правильный.
Метод 2 — Дополнительная матрица (может быть увеличена до любого размера)
ПРИМЕЧАНИЕ. Я оставил здесь метод 2 по историческим причинам. Мы будут использовать компьютеры, чтобы найти обратное (или, что более важно, решение системы уравнений) матриц больше, чем 2 × 2.
Если вам нужно найти обратное число 3 × 3 (или большего размера), используя бумагу, затем следуйте приведенным ниже инструкциям. Это утомительно, но вы туда доберетесь. Удачи.
Метод 2 использует сопряженную матрицу метод.
[Предупреждение: это долгая и древняя история!]
Ответ
Метод 2 (пример математики динозавров — должен исчезнуть)
Дана обратная матрица 3 × 3 по:
`A ^ -1 = (» adj «A) / (detA)`
«прил. A » — это сокращение от «примыкающий к A ».Мы используем кофакторы (которые мы встречали ранее), чтобы
определить сопряженных матрицы.
A » — это сокращение от «примыкающий к A ».Мы используем кофакторы (которые мы встречали ранее), чтобы
определить сопряженных матрицы.
Кофакторы
Напомним: Кофактор элемент в матрице — это значение, полученное путем оценки определитель, образованный элементами не в этой конкретной строке или столбец.
Пример 2а
Рассмотрим матрицу:
`((5,6,1), (0,3, -3), (4, -7,2))`
Кофактор 6 равен
.`| (0, -3), (4,2) | = 0 + 12 = 12`
Коэффициент -3 равен
.`| (5,6), (4, -7) | = -35-24 = -59`
Находим сопряженную матрицу заменой каждый элемент в матрице с его кофактором и добавлением + или — подписать:
`((+, -, +), (-, +, -), (+, -, +))`
, а затем найти транспонировать результирующая матрица. Транспонирование означает, что столбец 1 st становится столбцом 1 st строка; 2 nd столбец становится 2 nd ряд и т. д.
Транспонирование означает, что столбец 1 st становится столбцом 1 st строка; 2 nd столбец становится 2 nd ряд и т. д.
Пример 2b
Найти обратное методом сопряженных матриц:
`A = ((5,6,1), (0,3, -3), (4, -7,2))`
Решение
Шаг 1 :
Замените элементы сомножителями и примените + и —
`((+ (- 15), — (12), + (- 12)), (- (19), + (6), — (- 59)), (+ (- 21), — (- 15), + (15))) `
`= ((- 15, -12, -12), (- 19,6,59), (- 21,15,15))`
Шаг 2
Транспонировать матрицу:
`» adj «A = ((-15, -19, -21), (- 12,6,15), (- 12,59,15))`
Прежде чем мы сможем найти , инверсию матрицы A , нам понадобится det A:
`| (5,6,1), (0,3, -3), (4, -7,2) |` = 5 (-15) +4 (-21) `= -159`
Теперь у нас есть все необходимое для применения формулы
`A ^ -1 = (» adj «A) / detA`
Так
`A ^ -1 = (» adj «A) / detA`
`= 1 / -159 ((- 15, -19, -21), (- 12,6,15), (- 12,59,15))`
`A ^ -1 = ((0.
-1 = (» adj «A) / (detA)`
`= 1 / -60 ((- 12, -25, -21), (- 12, -10, -6), (- 12,10, -6))`
`= ((1 / 5,5 / 12,7 / 20), (1 / 5,1 / 6,1 / 10), (1/5, -1 / 6,1 / 10))`
`= ((0.2,0,417,0,35), (0,2,0,167,0,1), (0,2, -0,167,0,1)) `
Использование компьютера для поиска обратной матрицы
Теперь посмотрим, как делать все это более уместно с помощью компьютера …
Обращение больших матриц (метод 3)
Большинство реальных систем уравнений очень большие (обычно до 100 на 100). Мы используем компьютеры, чтобы найти эти инверсии. Вам нужно понять, что дать компьютеру и что он даст вам в ответ.
Однако некоторым нужно уметь находить инверсии больших матриц!
См. Обращение матрицы с помощью исключения Гаусса-Жордана для наиболее распространенного метода нахождения обратного.
Упражнение
Найдите число, обратное
.`((7, -2), (- 6,2))`
по методике 1.
-1 = 1 / (| A |) ((2,2), (6,7))`
`= 1/2 ((2,2), (6,7))`
`= ((1,1), (3,3.{-1} A \, = \, I_ {n}.
Если мы знаем это обратное, это в целом очень полезно. Например, оказывается, что обратная матрица
\ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right)
является
\ left (\ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right),
как можно быстро проверить:
\ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right) \ left (\ begin {array} {ccc} 4 & — 5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right) = \ left (\ begin {array} {ccc} 0-15 + 16 & 0 + 18-18 & 0 + 6-6 \\ 4 -20 + 16 & -5 + 24-18 & -2 + 8-6 \\ — 12 + 20-8 & 15-24 + 9 & 6-8 + 3 \ end {array} \ right) = \ left (\ begin {array} { ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right).
Теперь рассмотрим систему уравнений
\ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right) \ left (\ begin {array} {c} x \ \ y \\ z \ end {array} \ right) = \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right).
{- 1} \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right) = \ left ( \ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right) \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right) = \ left (\ begin {array} {c} 1 \\ — 2 \\ 2 \ end {array} \ right).
К сожалению, для больших квадратных матриц не существует четкой формулы для обратного. Действительно, поиск обратных чисел настолько трудоемок, что обычно не стоит усилий, и мы используем альтернативные методы для решения систем уравнений (см. Исключение Гаусса).
Однако иногда оно того стоит. Например, мы можем обнаружить, что хотим многократно решать
\ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right) \ left (\ begin {array} {c} x \ \ y \\ z \ end {array} \ right) = \ left (\ begin {array} {c} v_ {1} \\ v_ {2} \\ v_ {3} \ end {array} \ right)
для множества различных значений v_ {1}, v_ {2} и v_ {3}, и в этом случае зная, что обратное
\ left (\ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right)
очень пригодится.
Есть три основных метода поиска обратных. Первый метод, который называется методом кофакторов, подробно описан здесь. Второй называется исключением Гаусса-Жордана и рассматривается в другом месте. Третий использует так называемую теорему Кэли-Гамильтона: на одних курсах она рассматривается, а на других — нет.
Мы не будем здесь доказывать, что метод кофакторов работает; вместо этого мы представляем его просто как пошаговый рецепт.
Шаг 1: замените каждую запись ее второстепенной
Для данной записи в матрице 3 на 3 вычеркните всю ее строку и столбец и возьмите определитель оставшейся матрицы 2 на 2 (это называется второстепенным).
В нашем примере это дает нам
\ left (\ begin {array} {ccc} \ left (-4 \ right) \ times 1- \ left (-2 \ right) \ times 4 & 1 \ times 1- \ left (-2 \ right) \ times \ left (-3 \ right) & 1 \ times 4- \ left (-4 \ right) \ times \ left (-3 \ right) \\\ left (-3 \ right) \ times 1- \ left (-2 \ вправо) \ раз 4 и 0 \ раз 1- \ влево (-2 \ вправо) \ раз \ влево (-3 \ вправо) и 0 \ раз 4- \ влево (-3 \ вправо) \ раз \ влево (-3 \ вправо ) \\\ влево (-3 \ вправо) \ раз \ влево (-2 \ вправо) — \ влево (-2 \ вправо) \ раз \ влево (-4 \ вправо) & 0 \ раз \ влево (-2 \ вправо ) — \ left (-2 \ right) \ times 1 & 0 \ times \ left (-4 \ right) — \ left (-3 \ right) \ times 1 \ end {array} \ right) = \ left (\ begin { array} {ccc} 4 & -5 & -8 \\ 5 & -6 & -9 \\ — 2 & 2 & 3 \ end {array} \ right).
Шаг 2: измените некоторые знаки
Теперь меняем приметы некоторых несовершеннолетних по схеме
\ left (\ begin {array} {ccc} + & — & + \\ — & + & — \\ + & — & + \ end {array} \ right),
таким образом создавая так называемую матрицу кофакторов. В нашем случае это
\ left (\ begin {array} {ccc} 4 & 5 & -8 \\ — 5 & -6 & 9 \\ — 2 & -2 & 3 \ end {array} \ right).
Шаг 3: транспонировать
Теперь транспонируем матрицу сомножителей.В нашем случае мы получаем
\ left (\ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right).
Шаг 4: разделите на определитель
Наконец, делим на определитель исходной матрицы. В нашем случае определитель
\ text {det} \ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right) = 0 \ times \ text {det } \ left (\ begin {array} {cc} -4 & -2 \\ 4 & 1 \ end {array} \ right) +3 \ times \ text {det} \ left (\ begin {array} {cc} 1 & -2 \\ — 3 & 1 \ end {array} \ right) -2 \ times \ text {det} \ left (\ begin {array} {cc} 1 & -4 \\ — 3 & 4 \ end {array} \ right) = 1,
так что обратное просто
A ^ {- 1} = \ left (\ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right).{-1} [/ latex] равно единичной матрице . Единичная матрица — это квадратная матрица, содержащая единицы по главной диагонали и нули во всех остальных местах. Мы идентифицируем единичные матрицы как [latex] {I} _ {n} [/ latex], где [latex] n [/ latex] представляет размерность матрицы. Приведенные ниже уравнения представляют собой единичные матрицы для матрицы [latex] 2 \ text {} \ times \ text {} 2 [/ latex] и [latex] 3 \ text {} \ times \ text {} 3 [/ latex] матрица соответственно.
[латекс] {I} _ {2} = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right ] [/ латекс]
[латекс] {I} _ {3} = \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right] [/ latex]
Единичная матрица действует как 1 в матричной алгебре.{-1} [/ latex] уникален. Мы рассмотрим два метода поиска обратной матрицы [latex] 2 \ text {} \ times \ text {} 2 [/ latex] и третий метод, который можно использовать как для [latex] 2 \ text {} Матрицы \ times \ text {} 2 [/ latex] и [latex] 3 \ text {} \ times \ text {} 3 [/ latex].
Общее примечание: матрица идентичности и мультипликативная инверсия
Единичная матрица , [latex] {I} _ {n} [/ latex], представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули во всех остальных местах.
[латекс] \ begin {массив} {l} \ hfill \\ \ begin {array} {l} \ begin {array} {l} \ hfill \\ {I} _ {2} = \ left [\ begin { array} {rr} \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 \ end {array} \ right] \ begin {array} {cccc} & & & \ end {array} {I} _ {3} = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 0 & \ hfill 1 \ end {array} \ right ] \ hfill \ end {array} \ hfill \\ \ text {} 2 \ times 2 \ text {3} \ times 3 \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Если [latex] A [/ latex] представляет собой матрицу [latex] n \ times n [/ latex], а [latex] B [/ latex] — матрица [latex] n \ times n [/ latex], такая, что [ латекс] AB = BA = {I} _ {n} [/ latex], затем [latex] B = {A} ^ {- 1} [/ latex], мультипликативная инверсия матрицы [латекс] A [ /латекс].
Пример 1: Показывает, что матрица идентичности действует как 1
Дана матрица A , покажите, что [латекс] AI = IA = A [/ latex].
[латекс] A = \ left [\ begin {array} {cc} 3 & 4 \\ -2 & 5 \ end {array} \ right] [/ latex]
Решение
Используйте матричное умножение, чтобы показать, что произведение [латекс] A [/ latex] и идентичности равно произведению идентичности и A.
[латекс] AI = \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill 4 \\ \ hfill -2 & \ hfill & \ hfill 5 \ end {array} \ right] \ begin {array } {r} \ hfill \ end {array} \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right] = \ left [\ begin {array} {rrrr} \ hfill 3 \ cdot 1 + 4 \ cdot 0 & \ hfill & \ hfill & \ hfill 3 \ cdot 0 + 4 \ cdot 1 \\ \ hfill -2 \ cdot 1+ 5 \ cdot 0 & \ hfill & \ hfill & \ hfill -2 \ cdot 0 + 5 \ cdot 1 \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill 4 \\ \ hfill -2 & \ hfill & \ hfill 5 \ end {array} \ right] [/ latex]
[латекс] AI = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right] \ begin {array} {r} \ hfill \ end {array} \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill 4 \\ \ hfill -2 & \ hfill & \ hfill 5 \ end {array} \ right] = \ left [\ begin {array} {rrrr} \ hfill 1 \ cdot 3 + 0 \ cdot \ left (-2 \ right) & \ hfill & \ hfill & \ hfill 1 \ cdot 4 + 0 \ cdot 5 \\ \ hfill 0 \ cdot 3 + 1 \ cdot \ left (-2 \ right) & \ hfill & \ hfill & \ hfill 0 \ cdot 4 + 1 \ cdot 5 \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill 4 \\ \ hfill -2 & \ hfill & \ hfill 5 \ end {array} \ right] [/ latex]
Как сделать: даны две матрицы, покажите, что одна является мультипликативной инверсией другой.{-1} [/ латекс].
Пример 2: Отображение того, что матрица
A является мультипликативной обратной матрицей BПокажите, что данные матрицы мультипликативно инвертируют друг друга.
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 5 \\ \ hfill -2 & \ hfill & \ hfill -9 \ end {array} \ right], B = \ left [\ begin {array} {rrr} \ hfill -9 & \ hfill & \ hfill -5 \\ \ hfill 2 & \ hfill & \ hfill 1 \ end {array} \ right] [/ latex]
Решение
Умножьте [латекс] AB [/ латекс] и [латекс] BA [/ латекс].Если оба продукта равны идентичности, то две матрицы являются обратными друг другу.
[латекс] \ begin {array} {l} AB = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 5 \\ \ hfill -2 & \ hfill & \ hfill -9 \ end { array} \ right] \ cdot \ left [\ begin {array} {rrr} \ hfill -9 & \ hfill & \ hfill -5 \\ \ hfill 2 & \ hfill & \ hfill 1 \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {rrr} \ hfill 1 \ left (-9 \ right) +5 \ left (2 \ right) & \ hfill & \ hfill 1 \ left (-5 \ right) + 5 \ left (1 \ right) \\ \ hfill -2 \ left (-9 \ right) -9 \ left (2 \ right) & \ hfill & \ hfill -2 \ left (-5 \ right) -9 \ left (1 \ right) \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {ccc} 1 & & 0 \\ 0 & & 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]
[латекс] \ begin {array} {l} BA = \ left [\ begin {array} {rrr} \ hfill -9 & \ hfill & \ hfill -5 \\ \ hfill 2 & \ hfill & \ hfill 1 \ end { array} \ right] \ cdot \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 5 \\ \ hfill -2 & \ hfill & \ hfill -9 \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {rrr} \ hfill -9 \ left (1 \ right) -5 \ left (-2 \ right) & \ hfill & \ hfill -9 \ left (5 \ right) -5 \ left (-9 \ right) \\ \ hfill 2 \ left (1 \ right) +1 \ left (-2 \ right) & \ hfill & \ hfill 2 \ left (-5 \ right) +1 \ left (-9 \ right) \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {ccc} 1 & & 0 \\ 0 & & 1 \ end {array} \ right] \ hfill \ конец {array} [/ latex]
[латекс] A [/ latex] и [latex] B [/ latex] противоположны друг другу.
Попробуйте 1
Покажите, что следующие две матрицы инвертируют друг друга.
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 4 \\ \ hfill -1 & \ hfill & \ hfill -3 \ end {array} \ right], B = \ left [\ begin {array} {rrr} \ hfill -3 & \ hfill & \ hfill -4 \\ \ hfill 1 & \ hfill & \ hfill 1 \ end {array} \ right] [/ latex]
Нахождение обратного умножения с помощью умножения матрицы
Теперь мы можем определить, являются ли две матрицы инверсными, но как мы можем найти инверсию данной матрицы? Поскольку мы знаем, что произведение матрицы на обратную матрицу является единичной матрицей, мы можем найти обратную матрицу, составив уравнение с использованием умножения матриц .
Пример 3: Нахождение обратного умножения с помощью матричного умножения
Используйте умножение матриц, чтобы найти обратную матрицу.
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill -3 \ end {array} \ right] [/ latex ]
Решение
Для этого метода мы умножаем [latex] A [/ latex] на матрицу, содержащую неизвестные константы, и устанавливаем ее равной единице.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -3 \ end {array} \ right] \ text {} \ left [\ begin {array } {rr} \ hfill a & \ hfill b \\ \ hfill c & \ hfill d \ end {array} \ right] = \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 \ end {array} \ right] [/ latex]
Найдите произведение двух матриц, стоящих слева от знака равенства.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -3 \ end {array} \ right] \ text {} \ left [\ begin {array } {rr} \ hfill a & \ hfill b \\ \ hfill c & \ hfill d \ end {array} \ right] = \ left [\ begin {array} {rr} \ hfill 1a — 2c & \ hfill 1b — 2d \\ \ hfill 2a — 3c & \ hfill 2b — 3d \ end {array} \ right] [/ latex]
Затем создайте систему уравнений с записью в строке 1, столбце 1 новой матрицы, равной первой записи идентичности, 1. Установите запись в строке 2, столбце 1 новой матрицы, равной соответствующей запись идентичности, которая равна 0.
[латекс] \ begin {array} {c} 1a — 2c = 1 \ text {} {R} _ {1} \\ 2a — 3c = 0 \ text {} {R} _ {2} \ end {array } [/ latex]
Используя операции со строками, умножьте и сложите следующим образом: [latex] \ left (-2 \ right) {R} _ {1} + {R} _ {2} \ to {R} _ {2} [/ latex] . Сложите уравнения и решите для [латекс] c [/ латекс].
[латекс] \ begin {array} {r} \ hfill 1a — 2c = 1 \\ \ hfill 0 + 1c = -2 \\ \ hfill c = -2 \ end {array} [/ latex]
Обратный заменитель решить для [latex] a [/ latex].
[латекс] \ begin {array} {r} \ hfill a — 2 \ left (-2 \ right) = 1 \\ \ hfill a + 4 = 1 \\ \ hfill a = -3 \ end {array} [ / латекс]
Напишите другую систему уравнений, установив запись в строке 1, столбце 2 новой матрицы, равной соответствующей записи тождества, 0.Установите запись в строке 2, столбце 2, равной соответствующей записи идентификатора.
[латекс] \ begin {array} {rr} \ hfill 1b — 2d = 0 & \ hfill {R} _ {1} \\ \ hfill 2b — 3d = 1 & \ hfill {R} _ {2} \ end {массив } [/ latex]
Используя операции со строками, умножьте и сложите следующим образом: [latex] \ left (-2 \ right) {R} _ {1} + {R} _ {2} = {R} _ {2} [/ latex]. Сложите два уравнения и решите относительно [латекс] d [/ латекс].
[латекс] \ begin {array} {r} \ hfill 1b — 2d = 0 \\ \ hfill \ frac {0 + 1d = 1} {d = 1} \\ \ hfill \ end {array} [/ latex]
Еще раз выполните обратную замену и решите [латекс] b [/ латекс].{-1} [/ латекс].
Например, учитывая
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 2 & \ hfill & \ hfill 1 \\ \ hfill 5 & \ hfill & \ hfill 3 \ end {array} \ right] [/ latex]
augment [latex] A [/ latex] с идентификатором
[латекс] \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 1 \\ \ hfill 5 & \ hfill 3 \ end {array} \ text {} | \ text {} \ begin {array} {rr } \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 \ end {array} \ right] [/ latex]
Выполните операций со строками с целью превращения [latex] A [/ latex] в идентификатор.
- Поменять местами ряд 1 и ряд 2.
[латекс] \ left [\ begin {array} {rr} \ hfill 5 & \ hfill 3 \\ \ hfill 2 & \ hfill 1 \ end {array} \ text {} | \ text {} \ begin {array} {rr } \ hfill 0 & \ hfill 1 \\ \ hfill 1 & \ hfill 0 \ end {array} \ right] [/ latex]
- Умножить строку 2 на [latex] -2 [/ latex] и прибавить к строке 1.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 2 & \ hfill 1 \ end {array} \ text {} | \ text {} \ begin {array} {rr } \ hfill -2 & \ hfill 1 \\ \ hfill 1 & \ hfill 0 \ end {array} \ right] [/ latex]
- Умножить строку 1 на [latex] -2 [/ latex] и прибавить к строке 2.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { rr} \ hfill -2 & \ hfill 1 \\ \ hfill 5 & \ hfill -2 \ end {array} \ right] [/ latex]
- Добавьте строку 2 к строке 1.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { rr} \ hfill 3 & \ hfill -1 \\ \ hfill 5 & \ hfill -2 \ end {array} \ right] [/ latex]
- Умножить строку 2 на [latex] -1 [/ latex].{-1} = \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill -1 \\ \ hfill -5 & \ hfill & \ hfill 2 \ end {array} \ right] [/ latex]
Нахождение обратной мультипликативной матрицы 2 × 2 по формуле
Когда нам нужно найти мультипликативную обратную матрицы [latex] 2 \ times 2 [/ latex], мы можем использовать специальную формулу вместо умножения матриц или увеличения с тождеством. {- 1} = \ frac {1} {ad-bc} \ left [\ begin {array} {rrr} \ hfill d & \ hfill & \ hfill -b \\ \ hfill -c & \ hfill & \ hfill a \ end {array} \ right] [/ latex]
где [латекс] ad-bc \ ne 0 [/ латекс].{-1} = \ frac {1} {\ left (1 \ right) \ left (-3 \ right) — \ left (-2 \ right) \ left (2 \ right)} \ left [\ begin {массив } {cc} -3 & 2 \\ -2 & 1 \ end {array} \ right] \ hfill \\ = \ frac {1} {- 3 + 4} \ left [\ begin {array} {cc} -3 & 2 \\ -2 & 1 \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {cc} -3 & 2 \\ -2 & 1 \ end {array} \ right] \ hfill \ end { array} [/ latex]
Анализ решения
Мы можем проверить, работает ли наша формула, используя один из других методов вычисления обратного. Давайте дополним [latex] A [/ latex] идентичностью.
[латекс] \ left [\ begin {array} {cc} 1 & -2 \\ 2 & -3 \ end {array} | \ begin {array} {cc} 1 & 0 \\ 0 & 1 \ end {array} \ right ] [/ латекс]
Выполните операций со строками с целью превращения [latex] A [/ latex] в идентификатор.
- Умножьте строку 1 на [latex] -2 [/ latex] и прибавьте к строке 2.
[латекс] \ left [\ begin {array} {cc} 1 & -2 \\ 0 & 1 \ end {array} | \ begin {array} {cc} 1 & 0 \\ -2 & 1 \ end {array} \ right ] [/ латекс]
- Умножить строку 1 на 2 и прибавить к строке 1.{-1} = \ left [\ begin {array} {cc} -3 & 2 \\ -2 & 1 \ end {array} \ right] [/ latex]
Попробуйте 2
Используйте формулу, чтобы найти обратную матрицу [латекс] A [/ латекс]. Проверьте свой ответ, добавив единичную матрицу.
[латекс] A = \ left [\ begin {array} {cc} 1 & -1 \\ 2 & 3 \ end {array} \ right] [/ latex]
Пример 5: Нахождение обратной матрицы, если она существует
Найдите обратную матрицу, если она существует.
[латекс] A = \ left [\ begin {array} {cc} 3 & 6 \\ 1 & 2 \ end {array} \ right] [/ latex]
Решение
Мы будем использовать метод увеличения идентичности.
[латекс] \ left [\ begin {array} {cc} 3 & 6 \\ 1 & 3 \ end {array} | \ begin {array} {cc} 1 & 0 \\ 0 & 1 \ end {array} \ right] [ / латекс]
- Поменять местами ряд 1 и ряд 2.
[латекс] \ left [\ begin {array} {cc} 1 & 3 \\ 3 & 6 \ text {} \ end {array} \ text {} \ text {} \ text {} | \ begin {array} {cc } 0 & 1 \\ 1 & 0 \ end {array} \ right] [/ latex]
- Умножьте строку 1 на −3 и прибавьте ее к строке 2.
[латекс] \ left [\ begin {array} {cc} 1 & 2 \\ 0 & 0 \ end {array} | \ begin {array} {cc} 1 & 0 \\ -3 & 1 \ end {array} \ right] [/ латекс]
- Мы больше ничего не можем сделать.Нули в строке 2 означают, что эта матрица не имеет инверсии.
Нахождение обратной мультипликативной матрицы 3 × 3
К сожалению, у нас нет формулы, аналогичной формуле для матрицы [latex] 2 \ text {} \ times \ text {} 2 [/ latex], чтобы найти инверсию [latex] 3 \ text {} \ times \ text {} 3 [/ latex] матрица. Вместо этого мы дополним исходную матрицу единичной матрицей и будем использовать строковых операций для получения обратной.
Для матрицы [latex] 3 \ text {} \ times \ text {} 3 [/ latex]
[латекс] A = \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ right] [/ latex]
augment [latex] A [/ latex] с тождественной матрицей
[латекс] A | I = \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ text {} | \ text {} \ begin {array } {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] [/ latex]
Для начала запишем расширенную матрицу с идентичностью справа и [latex] A [/ latex] слева.Выполнив элементарные операции со строками так, чтобы слева появилась единичная матрица , мы получим справа обратную матрицу . Мы найдем инверсию этой матрицы в следующем примере.
Как: по матрице [latex] 3 \ times 3 [/ latex] найти обратную
- Запишите исходную матрицу, дополненную единичной матрицей справа.
- Используйте элементарные операции со строками, чтобы идентификатор отображался слева.
- То, что получается справа, является обратной по отношению к исходной матрице.{-1} A = I [/ латекс].
Пример 6: Нахождение обратной матрицы 3 × 3
Учитывая [латекс] 3 \ умножить на 3 [/ латекс] матрицу [латекс] A [/ латекс], найдите обратное.
[латекс] A = \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ right] [/ latex]
Решение
Дополните [latex] A [/ latex] единичной матрицей, а затем начните операции со строками, пока единичная матрица не заменит [latex] A [/ latex]. Матрица справа будет инверсией [latex] A [/ latex].
[латекс] \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} | \ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] \ stackrel {\ text {Interchange} {R} _ {2} \ text {и} {R} _ {1}} {\ to} \ left [\ begin {array} {ccc} 3 & 3 & 1 \\ 2 & 3 & 1 \\ 2 & 4 & 1 \ end {array} | \ begin {array} {ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {array } \ right] [/ latex]
[латекс] — {R} _ {2} + {R} _ {1} = {R} _ {1} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 2 & 3 & 1 \ \ 2 & 4 & 1 \ end {array} | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill 1 & \ hfill 0 & \ hfill 0 \\ \ hfill 0 & \ hfill 0 & \ hfill 1 \ end {array} \ right] [/ latex]
[латекс] — {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 2 & 3 & 1 \ \ 0 & 1 & 0 \ end {array} | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill 1 & \ hfill 0 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \ end {array} \ right] [/ latex]
[латекс] {R} _ {3} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 2 & 3 & 1 \ end {массив } | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 1 & \ hfill 0 & \ hfill 0 \ end {array} \ right ] [/ латекс]
[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 3 & 1 \ end {array} | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 3 & \ hfill -2 & \ hfill 0 \ end {array} \ right] [/ latex]
[латекс] -3 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 6 & \ hfill -2 & \ hfill -3 \ end {array} \ right] [/ latex]
Таким образом,
[латекс] {A} ^ {- 1} = B = \ left [\ begin {array} {ccc} -1 & 1 & 0 \\ -1 & 0 & 1 \\ 6 & -2 & -3 \ end {array} \ right ] [/ латекс]
Анализ решения
Чтобы доказать, что [latex] B = {A} ^ {- 1} [/ latex], давайте умножим две матрицы вместе, чтобы увидеть, совпадает ли продукт с тождеством, if [latex] A {A} ^ {- 1} = I [/ latex] и [latex] {A} ^ {- 1} A = I [/ latex].{-1} = \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ right] \ text {} \ left [\ begin {array} { rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 6 & \ hfill -2 & \ hfill -3 \ end {array} \ right] \ hfill \ end { массив} \ hfill \\ = \ left [\ begin {array} {ccc} 2 \ left (-1 \ right) +3 \ left (-1 \ right) +1 \ left (6 \ right) & 2 \ left (1 \ вправо) +3 \ влево (0 \ вправо) +1 \ влево (-2 \ вправо) и 2 \ влево (0 \ вправо) +3 \ влево (1 \ вправо) +1 \ влево (-3 \ вправо) \\ 3 \ влево (-1 \ вправо) +3 \ влево (-1 \ вправо) +1 \ влево (6 \ вправо) и 3 \ влево (1 \ вправо) +3 \ влево (0 \ вправо) +1 \ влево (-2 \ вправо) и 3 \ влево (0 \ вправо) +3 \ влево (1 \ вправо) +1 \ влево (-3 \ вправо) \\ 2 \ влево (-1 \ вправо) + 4 \ влево (-1 \ вправо) +1 \ влево (6 \ вправо) и 2 \ влево (1 \ вправо) +4 \ влево (0 \ вправо) +1 \ влево (-2 \ вправо) и 2 \ влево (0 \ right) +4 \ left (1 \ right) +1 \ left (-3 \ right) \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]
[латекс] \ begin {массив} {l} \ begin {array} {l} \ begin {array} {l} \ hfill \\ \ hfill \ end {array} \ hfill \\ {A} ^ {- 1 } A = \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 6 & \ hfill -2 & \ hfill -3 \ end {array} \ right] \ text {} \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ = \ left [\ begin {array} {rrr} \ hfill -1 \ left (2 \ right) +1 \ left (3 \ right) +0 \ left (2 \ right) & \ hfill -1 \ left (3 \ right) +1 \ left (3 \ right) +0 \ left (4 \ right) & \ hfill -1 \ left (1 \ right) +1 \ left (1 \ right) +0 \ left (1 \ right) \\ \ hfill -1 \ left (2 \ right) +0 \ left (3 \ right) +1 \ left (2 \ right) & \ hfill -1 \ left (3 \ right) +0 \ left (3 \ right) +1 \ left (4 \ right) & \ hfill -1 \ left (1 \ right) +0 \ left (1 \ right) +1 \ left (1 \ right) \\ \ hfill 6 \ left (2 \ right) + — 2 \ left (3 \ right) + — 3 \ left (2 \ right) & \ hfill 6 \ left (3 \ right) + — 2 \ left (3 \ right) + -3 \ left (4 \ right) & \ hfill 6 \ left (1 \ right) + — 2 \ left (1 \ right) + — 3 \ left (1 \ right) \ end {array} \ right] \ hfill \\ = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfil l 0 \\ \ hfill 0 & \ hfill 0 & \ hfill 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]
Попробовать 3
Найдите обратную матрицу [latex] 3 \ times 3 [/ latex]. {- 1} a = \ left (\ frac {1} {a} \ right) a = 1 [/ latex].{-1} [/ latex] равно единичной матрице . Единичная матрица — это квадратная матрица, содержащая единицы по главной диагонали и нули во всех остальных местах. Мы идентифицируем единичные матрицы как [latex] {I} _ {n} [/ latex], где [latex] n [/ latex] представляет размерность матрицы. Приведенные ниже уравнения представляют собой единичные матрицы для матрицы [latex] 2 \ text {} \ times \ text {} 2 [/ latex] и [latex] 3 \ text {} \ times \ text {} 3 [/ latex]. , соответственно.
[латекс] {I} _ {2} = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right ] [/ латекс]
[латекс] {I} _ {3} = \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right] [/ latex]
Единичная матрица действует как 1 в матричной алгебре.{-1} [/ latex] уникален. Мы рассмотрим два метода поиска обратной матрицы [latex] 2 \ text {} \ times \ text {} 2 [/ latex] и третий метод, который можно использовать как для [latex] 2 \ text {} Матрицы \ times \ text {} 2 [/ latex] и [latex] 3 \ text {} \ times \ text {} 3 [/ latex].
Общее примечание: матрица идентичности и мультипликативная инверсия
Единичная матрица , [latex] {I} _ {n} [/ latex], представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули во всех остальных местах.
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ {I} _ {2} & = \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 \ end {array} \ right] \ begin {array} {cccc} & & & \ end {array} & {I} _ {3} & = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 0 & \ hfill 1 \ end {array} \ right] \ hfill \\ & \ text { } 2 \ times 2 & & \ text {3} \ times 3 \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Если [latex] A [/ latex] представляет собой матрицу [latex] n \ times n [/ latex], а [latex] B [/ latex] — матрица [latex] n \ times n [/ latex], такая, что [ латекс] AB = BA = {I} _ {n} [/ latex], затем [latex] B = {A} ^ {- 1} [/ latex], мультипликативная инверсия матрицы [латекс] A [ /латекс].
Пример: демонстрация того, что матрица идентичности действует как 1
Дана матрица A , покажите, что [латекс] AI = IA = A [/ latex].
Показать решение
[латекс] A = \ left [\ begin {array} {cc} 3 & 4 \\ -2 & 5 \ end {array} \ right] [/ latex]Используйте матричное умножение, чтобы показать, что произведение [латекс] A [/ latex] и идентичности равно произведению идентичности и A.
[латекс] AI = \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill 4 \\ \ hfill -2 & \ hfill & \ hfill 5 \ end {array} \ right] \ begin {array } {r} \ hfill \ end {array} \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right] = \ left [\ begin {array} {rrrr} \ hfill 3 \ cdot 1 + 4 \ cdot 0 & \ hfill & \ hfill & \ hfill 3 \ cdot 0 + 4 \ cdot 1 \\ \ hfill -2 \ cdot 1+ 5 \ cdot 0 & \ hfill & \ hfill & \ hfill -2 \ cdot 0 + 5 \ cdot 1 \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill 4 \\ \ hfill -2 & \ hfill & \ hfill 5 \ end {array} \ right] [/ latex]
[латекс] AI = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right] \ begin {array} {r} \ hfill \ end {array} \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill 4 \\ \ hfill -2 & \ hfill & \ hfill 5 \ end {array} \ right] = \ left [\ begin {array} {rrrr} \ hfill 1 \ cdot 3 + 0 \ cdot \ left (-2 \ right) & \ hfill & \ hfill & \ hfill 1 \ cdot 4 + 0 \ cdot 5 \\ \ hfill 0 \ cdot 3 + 1 \ cdot \ left (-2 \ right) & \ hfill & \ hfill & \ hfill 0 \ cdot 4 + 1 \ cdot 5 \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill 3 & \ hfill & \ hfill 4 \\ \ hfill -2 & \ hfill & \ hfill 5 \ end {array} \ right] [/ latex]
Как сделать: даны две матрицы, покажите, что одна является мультипликативной обратной величиной другой
- Дана матрица [латекс] A [/ латекс] порядка [латекс] n \ умноженная на n [/ латекс] и матрица [латекс] B [/ латекс] порядка [латекс] n \ умноженная на n [/ латекс] умножить [ латекс] АВ [/ латекс].{-1} [/ латекс].
Пример: отображение этой матрицы
A является мультипликативной обратной матрицей BПокажите, что данные матрицы мультипликативно инвертируют друг друга.
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 5 \\ \ hfill -2 & \ hfill & \ hfill -9 \ end {array} \ right], B = \ left [\ begin {array} {rrr} \ hfill -9 & \ hfill & \ hfill -5 \\ \ hfill 2 & \ hfill & \ hfill 1 \ end {array} \ right] [/ latex]
Показать решениеУмножьте [латекс] AB [/ латекс] и [латекс] BA [/ латекс].Если оба продукта равны идентичности, то две матрицы являются обратными друг другу.
[латекс] \ begin {массив} {l} AB & = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 5 \\ \ hfill -2 & \ hfill & \ hfill -9 \ end {массив} \ right] \ cdot \ left [\ begin {array} {rrr} \ hfill -9 & \ hfill & \ hfill -5 \\ \ hfill 2 & \ hfill & \ hfill 1 \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {rrr} \ hfill 1 \ left (-9 \ right) +5 \ left (2 \ right) & \ hfill & \ hfill 1 \ left (-5 \ right ) +5 \ left (1 \ right) \\ \ hfill -2 \ left (-9 \ right) -9 \ left (2 \ right) & \ hfill & \ hfill -2 \ left (-5 \ right) — 9 \ left (1 \ right) \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {ccc} 1 & & 0 \\ 0 & & 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]
[латекс] \ begin {массив} {l} BA & = \ left [\ begin {array} {rrr} \ hfill -9 & \ hfill & \ hfill -5 \\ \ hfill 2 & \ hfill & \ hfill 1 \ end {массив} \ right] \ cdot \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 5 \\ \ hfill -2 & \ hfill & \ hfill -9 \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {rrr} \ hfill -9 \ left (1 \ right) -5 \ left (-2 \ right) & \ hfill & \ hfill -9 \ left (5 \ right) -5 \ left (-9 \ right) \\ \ hfill 2 \ left (1 \ right) +1 \ left (-2 \ right) & \ hfill & \ hfill 2 \ left (-5 \ right) + 1 \ left (-9 \ right) \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {ccc} 1 & & 0 \\ 0 & & 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]
[латекс] A [/ latex] и [latex] B [/ latex] противоположны друг другу.
Попробуйте
Покажите, что следующие две матрицы инвертируют друг друга.
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 4 \\ \ hfill -1 & \ hfill & \ hfill -3 \ end {array} \ right], B = \ left [\ begin {array} {rrr} \ hfill -3 & \ hfill & \ hfill -4 \\ \ hfill 1 & \ hfill & \ hfill 1 \ end {array} \ right] [/ latex]
Показать решение[латекс] \ begin {array} {l} AB = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 4 \\ \ hfill -1 & \ hfill & \ hfill -3 \ end { array} \ right] \ begin {array} {r} \ hfill \ end {array} \ left [\ begin {array} {rrr} \ hfill -3 & \ hfill & \ hfill -4 \\ \ hfill 1 & \ hfill & \ hfill 1 \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill 1 \ left (-3 \ right) +4 \ left (1 \ right) & \ hfill & \ hfill 1 \ left (-4 \ right) +4 \ left (1 \ right) \\ \ hfill -1 \ left (-3 \ right) + — 3 \ left (1 \ right) & \ hfill & \ hfill -1 \ left (-4 \ right) + — 3 \ left (1 \ right) \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right] \ hfill \\ BA = \ left [\ begin {array} {rrr} \ hfill -3 & \ hfill & \ hfill -4 \\ \ hfill 1 & \ hfill & \ hfill 1 \ end {array} \ right] \ begin {array} {r} \ hfill \ end {array} \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 4 \\ \ hfill -1 & \ hfill & \ hfill -3 \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill -3 \ left (1 \ right) + — 4 \ left (-1 \ right) & \ hfill & \ hfill -3 \ left (4 \ right) + — 4 \ left (-3 \ right) \\ \ hfill 1 \ left (1 \ right) +1 \ left (-1 \ r ight) & \ hfill & \ hfill 1 \ left (4 \ right) +1 \ left (-3 \ right) \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill 0 \\ \ hfill 0 & \ hfill & \ hfill 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]
Нахождение обратного умножения с помощью умножения матрицы
Теперь мы можем определить, являются ли две матрицы инверсными, но как мы можем найти инверсию данной матрицы? Поскольку мы знаем, что произведение матрицы на обратную матрицу является единичной матрицей, мы можем найти обратную матрицу, составив уравнение с использованием умножения матриц .
Пример: поиск обратного умножения с помощью умножения матрицы
Используйте умножение матриц, чтобы найти обратную матрицу.
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill -3 \ end {array} \ right] [/ latex ]
Показать решениеДля этого метода мы умножаем [latex] A [/ latex] на матрицу, содержащую неизвестные константы, и устанавливаем ее равной единице.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -3 \ end {array} \ right] \ text {} \ left [\ begin {array } {rr} \ hfill a & \ hfill b \\ \ hfill c & \ hfill d \ end {array} \ right] = \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 \ end {array} \ right] [/ latex]
Найдите произведение двух матриц, стоящих слева от знака равенства.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -3 \ end {array} \ right] \ text {} \ left [\ begin {array } {rr} \ hfill a & \ hfill b \\ \ hfill c & \ hfill d \ end {array} \ right] = \ left [\ begin {array} {rr} \ hfill 1a — 2c & \ hfill 1b — 2d \\ \ hfill 2a — 3c & \ hfill 2b — 3d \ end {array} \ right] [/ latex]
Затем создайте систему уравнений с записью в строке 1, столбце 1 новой матрицы, равной первой записи идентичности, 1. Установите запись в строке 2, столбце 1 новой матрицы, равной соответствующей запись идентичности, которая равна 0.
[латекс] \ begin {array} {c} 1a — 2c = 1 \ text {} {R} _ {1} \\ 2a — 3c = 0 \ text {} {R} _ {2} \ end {array } [/ latex]
Используя операции со строками, умножьте и сложите следующим образом: [latex] \ left (-2 \ right) {R} _ {1} + {R} _ {2} \ to {R} _ {2} [/ latex] . Сложите уравнения и решите для [латекс] c [/ латекс].
[латекс] \ begin {array} {r} \ hfill 1a — 2c = 1 \\ \ hfill 0 + 1c = -2 \\ \ hfill c = -2 \ end {array} [/ latex]
Обратный заменитель решить для [latex] a [/ latex].
[латекс] \ begin {array} {r} \ hfill a — 2 \ left (-2 \ right) = 1 \\ \ hfill a + 4 = 1 \\ \ hfill a = -3 \ end {array} [ / латекс]
Напишите другую систему уравнений, установив запись в строке 1, столбце 2 новой матрицы, равной соответствующей записи тождества, 0.Установите запись в строке 2, столбце 2, равной соответствующей записи идентификатора.
[латекс] \ begin {array} {rr} \ hfill 1b — 2d = 0 & \ hfill {R} _ {1} \\ \ hfill 2b — 3d = 1 & \ hfill {R} _ {2} \ end {массив } [/ latex]
Используя операции со строками, умножьте и сложите следующим образом: [latex] \ left (-2 \ right) {R} _ {1} + {R} _ {2} = {R} _ {2} [/ latex]. Сложите два уравнения и решите относительно [латекс] d [/ латекс].
[латекс] \ begin {array} {r} \ hfill 1b — 2d = 0 \\ \ hfill \ frac {0 + 1d = 1} {d = 1} \\ \ hfill \ end {array} [/ latex]
Еще раз выполните обратную замену и решите [латекс] b [/ латекс].{-1} [/ латекс].
Например, учитывая
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 2 & \ hfill & \ hfill 1 \\ \ hfill 5 & \ hfill & \ hfill 3 \ end {array} \ right] [/ latex]
augment [latex] A [/ latex] с идентификатором
[латекс] \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 1 \\ \ hfill 5 & \ hfill 3 \ end {array} \ text {} | \ text {} \ begin {array} {rr } \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 \ end {array} \ right] [/ latex]
Выполните операций со строками с целью превращения [latex] A [/ latex] в идентификатор.
- Переключить строку 1 и строку 2.
[latex] \ left [\ begin {array} {rr} \ hfill 5 & \ hfill 3 \\ \ hfill 2 & \ hfill 1 \ end {array} \ text {} | \ text {} \ begin {array} {rr} \ hfill 0 & \ hfill 1 \\ \ hfill 1 & \ hfill 0 \ end {array} \ right] [/ latex]- Умножьте строку 2 на [latex] -2 [/ latex] и добавьте к строке 1.
[latex] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 2 & \ hfill 1 \ end {array} \ text {} | \ text {} \ begin {array} {rr} \ hfill -2 & \ hfill 1 \\ \ hfill 1 & \ hfill 0 \ end {array} \ right] [/ latex]- Умножить строку 1 на [latex] -2 [/ latex] и прибавить к строке 2.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { rr} \ hfill -2 & \ hfill 1 \\ \ hfill 5 & \ hfill -2 \ end {array} \ right] [/ latex]- Добавить строку 2 в строку 1.
[latex] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} {rr} \ hfill 3 & \ hfill -1 \\ \ hfill 5 & \ hfill -2 \ end {array} \ right] [/ latex]- Умножить строку 2 на [latex] -1 [/ latex]. {- 1} = \ frac {1} {ad-bc} \ left [\ begin {array} {rrr} \ hfill d & \ hfill & \ hfill -b \\ \ hfill -c & \ hfill & \ hfill a \ end {array} \ right] [/ latex]
где [латекс] ad-bc \ ne 0 [/ латекс].{-1} & = \ frac {1} {\ left (1 \ right) \ left (-3 \ right) — \ left (-2 \ right) \ left (2 \ right)} \ left [\ begin { array} {cc} -3 & 2 \\ -2 & 1 \ end {array} \ right] \ hfill \\ & = \ frac {1} {- 3 + 4} \ left [\ begin {array} {cc} — 3 & 2 \\ -2 & 1 \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {cc} -3 & 2 \\ -2 & 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]
Анализ решения
Мы можем проверить, работает ли наша формула, используя один из других методов вычисления обратного. Давайте дополним [latex] A [/ latex] идентичностью.
[латекс] \ left [\ begin {array} {cc} 1 & -2 \\ 2 & -3 \ end {array} | \ begin {array} {cc} 1 & 0 \\ 0 & 1 \ end {array} \ right ] [/ латекс]
Выполните операций со строками с целью превращения [latex] A [/ latex] в идентификатор.
- Умножьте строку 1 на [latex] -2 [/ latex] и добавьте к строке 2.
[latex] \ left [\ begin {array} {cc} 1 & -2 \\ 0 & 1 \ end {array} | \ begin {array} {cc} 1 & 0 \\ -2 & 1 \ end {array} \ right] [/ latex]- Умножить строку 1 на 2 и прибавить к строке 1.{-1} = \ left [\ begin {array} {cc} \ frac {3} {5} & \ frac {1} {5} \\ — \ frac {2} {5} & \ frac {1} {5} \ end {array} \ right] [/ latex]
Пример: поиск обратной матрицы, если она существует
Найдите обратную матрицу, если она существует.
[латекс] A = \ left [\ begin {array} {cc} 3 & 6 \\ 1 & 2 \ end {array} \ right] [/ latex]
Показать решениеМы будем использовать метод увеличения идентичности.
[латекс] \ left [\ begin {array} {cc} 3 & 6 \\ 1 & 2 \ end {array} | \ begin {array} {cc} 1 & 0 \\ 0 & 1 \ end {array} \ right] [ / латекс]
- Поменять местами ряд 1 и ряд 2.
[латекс] \ left [\ begin {array} {cc} 1 & 2 \\ 3 & 6 \ text {} \ end {array} \ text {} \ text {} \ text {} | \ begin {array} {cc } 0 & 1 \\ 1 & 0 \ end {array} \ right] [/ latex]- Умножьте строку 1 на −3 и добавьте ее к строке 2.
[latex] \ left [\ begin {array} {cc} 1 & 2 \\ 0 & 0 \ end {array} | \ begin {array} {cc} 1 & 0 \\ 1 & -3 \ end {array} \ right] [/ latex]- Мы больше ничего не можем сделать. Нули в строке 2 означают, что эта матрица не имеет инверсии.
Нахождение обратной мультипликативной матрицы 3 × 3
К сожалению, у нас нет формулы, аналогичной формуле для матрицы [latex] 2 \ text {} \ times \ text {} 2 [/ latex], чтобы найти инверсию [latex] 3 \ text {} \ times \ text {} 3 [/ latex] матрица.Вместо этого мы дополним исходную матрицу единичной матрицей и будем использовать строковых операций для получения обратной.
Для матрицы [latex] 3 \ text {} \ times \ text {} 3 [/ latex]
[латекс] A = \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ right] [/ latex]
augment [latex] A [/ latex] с тождественной матрицей
[латекс] A | I = \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ text {} | \ text {} \ begin {array } {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] [/ latex]
Для начала запишем расширенную матрицу с идентичностью справа и [latex] A [/ latex] слева.Выполнив элементарные операции со строками так, чтобы слева появилась единичная матрица , мы получим справа обратную матрицу . Мы найдем инверсию этой матрицы в следующем примере.
Как: по матрице [latex] 3 \ times 3 [/ latex] найти обратную
- Запишите исходную матрицу, дополненную единичной матрицей справа.
- Используйте элементарные операции со строками, чтобы идентификатор отображался слева.
- То, что получается справа, является обратной по отношению к исходной матрице.{-1} A = I [/ латекс].
Пример: поиск обратной матрицы 3 × 3
Учитывая [латекс] 3 \ умножить на 3 [/ латекс] матрицу [латекс] A [/ латекс], найдите обратное.
[латекс] A = \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ right] [/ latex]
Показать решениеДополните [latex] A [/ latex] единичной матрицей, а затем начните операции со строками, пока единичная матрица не заменит [latex] A [/ latex]. Матрица справа будет инверсией [latex] A [/ latex].
[латекс] \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} | \ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] \ stackrel {\ text {Interchange} {R} _ {2} \ text {и} {R} _ {1}} {\ to} \ left [\ begin {array} {ccc} 3 & 3 & 1 \\ 2 & 3 & 1 \\ 2 & 4 & 1 \ end {array} | \ begin {array} {ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \ end {array } \ right] [/ latex]
[латекс] — {R} _ {2} + {R} _ {1} = {R} _ {1} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 2 & 3 & 1 \ \ 2 & 4 & 1 \ end {array} | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill 1 & \ hfill 0 & \ hfill 0 \\ \ hfill 0 & \ hfill 0 & \ hfill 1 \ end {array} \ right] [/ latex]
[латекс] — {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 2 & 3 & 1 \ \ 0 & 1 & 0 \ end {array} | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill 1 & \ hfill 0 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \ end {array} \ right] [/ latex]
[латекс] {R} _ {3} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 2 & 3 & 1 \ end {массив } | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 1 & \ hfill 0 & \ hfill 0 \ end {array} \ right ] [/ латекс]
[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 3 & 1 \ end {array} | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 3 & \ hfill -2 & \ hfill 0 \ end {array} \ right] [/ latex]
[латекс] -3 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} | \ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 6 & \ hfill -2 & \ hfill -3 \ end {array} \ right] [/ latex]
Таким образом,
[латекс] {A} ^ {- 1} = B = \ left [\ begin {array} {ccc} -1 & 1 & 0 \\ -1 & 0 & 1 \\ 6 & -2 & -3 \ end {array} \ right ] [/ латекс]
Анализ решения
Чтобы доказать, что [latex] B = {A} ^ {- 1} [/ latex], давайте умножим две матрицы вместе, чтобы увидеть, совпадает ли продукт с тождеством, if [latex] A {A} ^ {- 1} = I [/ latex] и [latex] {A} ^ {- 1} A = I [/ latex].{-1} & = \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ right] \ text {} \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 6 & \ hfill -2 & \ hfill -3 \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {ccc} 2 \ left (-1 \ right) +3 \ left (-1 \ right) +1 \ left (6 \ right) & 2 \ left (1 \ right) +3 \ влево (0 \ вправо) +1 \ влево (-2 \ вправо) и 2 \ влево (0 \ вправо) +3 \ влево (1 \ вправо) +1 \ влево (-3 \ вправо) \\ 3 \ влево (-1 \ вправо) +3 \ влево (-1 \ вправо) +1 \ влево (6 \ вправо) и 3 \ влево (1 \ вправо) +3 \ влево (0 \ вправо) +1 \ влево ( -2 \ вправо) и 3 \ влево (0 \ вправо) +3 \ влево (1 \ вправо) +1 \ влево (-3 \ вправо) \\ 2 \ влево (-1 \ вправо) +4 \ влево (- 1 \ вправо) +1 \ влево (6 \ вправо) и 2 \ влево (1 \ вправо) +4 \ влево (0 \ вправо) +1 \ влево (-2 \ вправо) и 2 \ влево (0 \ вправо) +4 \ left (1 \ right) +1 \ left (-3 \ right) \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]
[latex] \ begin {array} {l} \ begin {array} {l} \ hfill \\ \ hfill \ end {array} \ hfill \\ {A} ^ {- 1} A & = \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill 1 & \ hfill 0 \\ \ hfill -1 & \ hfill 0 & \ hfill 1 \\ \ hfill 6 & \ hfill -2 & \ hfill -3 \ end {array} \ right] \ text {} \ left [\ begin {array} {ccc} 2 & 3 & 1 \\ 3 & 3 & 1 \\ 2 & 4 & 1 \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {rrr} \ hfill -1 \ left (2 \ right) +1 \ left (3 \ right) +0 \ left (2 \ right) & \ hfill -1 \ left (3 \ right) +1 \ left (3 \ right) +0 \ left (4 \ right) & \ hfill -1 \ left (1 \ right ) +1 \ влево (1 \ вправо) +0 \ влево (1 \ вправо) \\ \ hfill -1 \ влево (2 \ вправо) +0 \ влево (3 \ вправо) +1 \ влево (2 \ вправо) & \ hfill -1 \ left (3 \ right) +0 \ left (3 \ right) +1 \ left (4 \ right) & \ hfill -1 \ left (1 \ right) +0 \ left (1 \ right ) +1 \ left (1 \ right) \\ \ hfill 6 \ left (2 \ right) + — 2 \ left (3 \ right) + — 3 \ left (2 \ right) & \ hfill 6 \ left (3 \ right) + — 2 \ left (3 \ right) + — 3 \ left (4 \ right) & \ hfill 6 \ left (1 \ right) + — 2 \ left (1 \ right) + — 3 \ left ( 1 \ right) \ end {array} \ right] \ hfill \\ & = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill 0 \ \ \ hfill 0 & \ hfill 0 & \ hfill 1 \ end {array} \ right] \ hfill \ end {array} [/ latex]Попробуйте
Найдите обратную матрицу [latex] 3 \ times 3 [/ latex].{-1} = \ left [\ begin {array} {ccc} 1 & 1 & 2 \\ 2 & 4 & -3 \\ 3 & 6 & -5 \ end {array} \ right] [/ latex]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Обратная квадратная матрица
6.3 — Обратная квадратная матрицаРеальные числа
При работе с действительными числами уравнение ax = b может быть решено относительно x путем деления обоих стороны уравнения на a, чтобы получить x = b / a, пока a не было равным нулю.Поэтому казалось бы логичным что при работе с матрицами можно взять матричное уравнение AX = B и разделить оба сторон на A, чтобы получить X = B / A.
Однако это не сработает, потому что …
Нет матричного деления!
Хорошо, скажете вы. Вычитание было определено в терминах сложения, а деление — в терминах умножение. Поэтому вместо деления я просто умножу на обратное. Так оно и есть должно быть сделано.
Обратная матрица
Итак, что есть инверсия матрицы?
Ну, в реальных числах, обратное любому действительному числу a было числом a -1 , так что a умножить на a -1 равняется 1.Мы знали, что для действительного числа обратное число было обратным число, если число не было нулем.
Обратной квадратной матрице A, обозначенной A -1 , является матрица так что произведение A и A -1 — это матрица идентичности. Идентификационная матрица, которая дает будет того же размера, что и матрица A. Вау, есть а много общего между действительными числами и матрицами. Это хорошо, правда — ты не хочу это быть что-то совсем другое.
A (A -1 ) = I или A -1 (A) = I
Но есть несколько исключений. Прежде всего, А -1 делает не значит 1 / A. Помните: «Матричного деления нет!» Во-вторых, А -1 делает не означает брать обратную величину каждого элемента в матрице А.
Требования к инверсу
- Матрица должна быть квадратной (одинаковое количество строк и столбцов).
- Определитель матрицы не должен быть нулевым (определители рассматриваются в разделе 6.4). Это вместо того, чтобы действительное число не равнялось нулю, чтобы иметь обратное, определитель не должен равняться нулю, чтобы иметь обратное.
Квадратная матрица, имеющая обратную, называется обратимой или невырожденной . Матрица, которая не у инверсии называется в единственном числе .
Матрица не обязательно должна иметь обратную, но если она есть, то обратная матрица уникальна.
Трудный путь в поисках обратного
Матрица, обратная матрице A, будет удовлетворять уравнению A (A -1 ) = I.
- Присоедините единичную матрицу к правой части исходной матрицы, чтобы у вас есть A слева и единичная матрица справа. Это будет выглядеть так [A | I].
- Строка-уменьшить (предлагаю использовать поворот) матрицу пока в левой части не появится матрица идентичности. Когда левая сторона — это личность матрица правая сторона будет Обратной [I | А -1 ]. Если вы не можете чтобы получить единичную матрицу в левой части, тогда матрица сингулярна и не имеет обратного.
- Возьмите расширенную матрицу с правой стороны и назовите ее обратной.
Ярлык для поиска инверсии матрицы 2 × 2
Матрица, обратная матрице 2 × 2, может быть найдена с помощью …
- Переключить элементы по главной диагонали
- Возьмите противоположность двух других элементов
- Делим все значения на определитель матрицы (так как мы не говорили о детерминанте, для системы 2 × 2 это произведение элементов на главной диагонали за вычетом произведения двух других элементов).
Пример ярлыка
Поехали с оригинальной матрицей
Шаг 1, переключение элементов на главной диагонали повлечет за собой переключение 5 и 7.
Шаг 2, возьмите противоположность двух других элементов, но оставьте их там, где они есть.
Шаг 3, найдите определитель и разделите на него каждый элемент. Определитель это произведение элементов на главной диагонали за вычетом произведения элементы от главной диагонали.Это означает, что определитель этой матрицы равен 7 (5) — (-3) (2) = 35 + 6 = 41. Делим каждый элемент на 41.
Матрица, обратная исходной матрице …
5/41 2/41 -3/41 7/41 Теперь, вы говорите, подождите минутку — вы сказали, что не было матричного деления. Деления по матрице нет. Вы можете умножить или разделить матрицу на скаляр (действительное число) и определитель является скаляром.
Использование калькулятора
Теперь, когда вы знаете, как найти единичную матрицу вручную, поговорим о практичности. Калькулятор сделаю это за вас.
Вход в матрицу
- Нажмите клавишу Matrix (справа под клавишей X). На TI-83 + вам понадобится чтобы поразить 2 и Matrix.
- Стрелка к подменю Правка.
- Выберите матрицу для работы. У вас есть пять вариантов на выбор с TI-82 и десять на выбор. выбирайте из с TI-83.Обычно вы будете использовать [A]. Старайтесь избегать использования [E] для неуказанные причины, которые будут указаны, если вы изучаете конечную математику.
- Введите количество строк, нажмите клавишу ВВОД, а затем введите количество столбцов, а затем входить.
- Теперь вы вводите каждый элемент в матрицу, читая слева направо и сверху вниз. Нажмите введите после каждого числа. Вы можете использовать клавиши со стрелками для перемещения, если вы допустили ошибку.
- Закройте (2 nd Mode), когда вы закончите вводить все числа.
Использование матриц
Всякий раз, когда вам нужно получить доступ к созданной вами матрице, просто нажмите клавишу Matrix и выберите соответствующая матрица. Я бы посоветовал вам начать использовать Матрицу 1, Матрицу 2 и т. Д. Вместо Матрица, стрелка вниз, ввод. Это будет происходить быстрее, и вы будете много делать с этими матрицами.
Нахождение обратной матрицы на калькуляторе
Введите выражение [A] -1 , перейдя в Матрицу 1 и нажав клавишу x -1 .(-1).
Возможно, вам придется использовать клавиши со стрелками вправо или влево, чтобы прокрутить всю матрицу, чтобы записать ее вниз. По возможности дайте точные ответы.
Один из способов дать точный ответ — это заставить калькулятор переводить десятичные дроби в дроби для ты. В конце концов, дроби действительно ваши друзья (и я серьезно это имею в виду). Вы можете получить Калькулятор выполняет преобразование десятичной дроби в дробную, нажимая Math, Enter, Enter.
Также, если вы получите ответ типа 1.2E-12, шансы действительно хорошо, что число равно нулю, и это из-за неточности в калькуляторе что вы получаете такой ответ. Преобразуйте число до нуля.
Зачем понадобился инверс?
Я так рад, что вы спросили об этом.
Одно из основных применений обратного преобразования — решение системы линейных уравнений. Вы можете записать систему в матричной форме как AX = B.
Теперь предварительно умножьте обе части на обратную величину A. Убедитесь, что вы соблюдаете эти два условия.
- Вы должны разместить инверсную матрицу рядом с матрицей. Это потому что инверсии должны быть рядом друг с другом (математически очень расплывчато, но вернемся к функциям), чтобы уничтожить друг друга.
- Если вы умножаете, помещая что-то перед левой стороной (предварительное умножение), он должен идти впереди правой стороны. Если вы положите что-то позади (пост-умножение) левой стороны, она должна идти позади правой стороны.
Умножение матриц НЕ коммутативно!
A -1 (AX) = A -1 (B)… предварительное умножение с обеих сторон по А -1
(A -1 A) X = A -1 B … используйте ассоциативный свойство для перегруппировки факторов
I X = A -1 B … при умножении на обратное вместе они становятся единичной матрицей
X = A -1 B … единичная матрица похожа на умножение на 1.
Если AX = B, то X = A -1 B
Итак, вы обычно цинично спрашиваете: «Вы только что решили другое уравнение, что это имеет отношение к чему-нибудь? »
Решение систем линейных уравнений
Рассмотрим систему линейных уравнений
3x + 2y - 5z = 12 х - 3у + 2z = -13 5х - у + 4z = 10Запишите коэффициенты в матрицу A.
х y z 3 2 -5 1 -3 2 5 -1 4 Запишите переменные в матрицу X.
Запишите константы в матрицу B.
12 -13 10 Убедитесь, что AX = B
Этот шаг на самом деле не нужен, но я хотел показать вам, что это действительно работает.
AX будет (3 × 3) × (3 × 1) = 3 × 1 матрица. Матрица B также является матрицей 3 × 1, поэтому, по крайней мере, размеры работать правильно.
Вот A, умноженное на X.
3 2 -5 х 3x + 2y — 5z 1 -3 2 y = 1x — 3y + 2z 5 -1 4 z 5x — 1y + 4z Обратите внимание, что это левая часть системы уравнений.В B — правая часть, значит, мы достигли равенства. Woohoo! Ты можешь написать система линейных уравнений в виде AX = B.
Итак, если вы можете написать систему линейных уравнений как AX = B, где A — коэффициент матрица, X — переменная матрица, а B — правая часть, вы можете найти решение системы X = A -1 B.
Поместите матрицу коэффициентов в [A] на калькуляторе и с правой стороны. стороной в [B].
Если вы попросили калькулятор найти обратный коэффициент матрица, это даст вам это для A -1
5/44 3/88 1/8 -3/44 -37/88 1/8 -7/44 -13/88 1/8 Вы можете сделать это, а затем умножить это на B, но было бы проще просто поместить все выражение в калькулятор и сразу получить ответ.Даже то, что показано ниже, — это больше работы, чем необходимо.
X = A -1 B = …
х 5/44 3/88 1/8 12 191/88 y = -3/44 -37/88 1/8 -13 = 519/88 z -7/44 -13/88 1/8 10 111/88 Итак, x = 191/88, y = 519/88 и z = 111/88.Это было бы настоящим боль решать вручную.
Это просто, почему мы не всегда так делаем?
Основная причина в том, что это не всегда работает.
- Инверсии существуют только для квадратных матриц. Это означает, что если вы не то же самое количество уравнений как переменных, то вы не можете использовать этот метод.
- Не каждая квадратная матрица имеет инверсию. Если матрица коэффициентов A равна единственное число (не имеет обратного), то решения может не быть или может быть много решений, но мы не можем сказать, что это такое.
- Перевертыши сложно найти вручную. Если у вас есть калькулятор, его нет так плохо, но помните, что калькуляторы не всегда дают вам ответ, который вы находясь в поиске.
обратных матричных вопросов с решениями
Пример 2
Найти матрицу, обратную матрице A: \ [A = \ begin {bmatrix} 1 и 1 \ 2 и 4 \ end {bmatrix} \] если он существует. {- 1} = \ begin {bmatrix} 2 & -1 / 2 \\ — 1 & 1/2 \ end {bmatrix} \]Пример 3
Найти матрицу, обратную матрице A:
\ [ A = \ begin {bmatrix} -2 & 2 & 0 \\ 2 & 1 & 3 \\ -2 & 4 & -2 \ end {bmatrix} \] если он существует.
Решение
Запишите расширенную матрицу \ ([A | I) \) \ [\ begin {bmatrix} -2 & 2 & 0 & | & 1 & 0 & 0 \\ 2 & 1 & 3 & | & 0 & 1 & 0 \\ -2 & 4 & -2 & | & 0 & 0 & 1 \ end {bmatrix} \] шаг 1 \ [ \ color {red} {\ begin {matrix} \\ R_2 + R_1 \\ R_3 — R_1 \ end {matrix}} \ begin {bmatrix} -2 & 2 & 0 & | & 1 & 0 & 0 \\ 0 & 3 & 3 & | & 1 & 1 & 0 \\ 0 & 2 & -2 & | & -1 & 0 & 1 \ end {bmatrix} \] шаг 2 \ [ \ color {red} {\ begin {matrix} \\ \\ R_3 — (2/3) R_2 \\ \ end {matrix}} \ begin {bmatrix} -2 & 2 & 0 & | & 1 & 0 & 0 \\ 0 & 3 & 3 & | & 1 & 1 & 0 \\ 0 & 0 & — 4 & | & -5/3 & -2/3 & 1 \ end {bmatrix} \] шаг 3 \ [ \красный цвет}{ \ begin {matrix} \\ \\ (-1/4) R_3 \\ \ end {matrix}} \ begin {bmatrix} -2 & 2 & 0 & | & 1 & 0 & 0 \\ 0 & 3 & 3 & | & 1 & 1 & 0 \\ 0 & 0 & 1 & | & 5/12 & 1/6 & -1/4 \ end {bmatrix} \] шаг 4 \ [ \красный цвет}{ \ begin {matrix} \\ R_2 — 3 \ раза R_3 \\ \\ \ end {matrix}} \ begin {bmatrix} -2 & 2 & 0 & | & 1 & 0 & 0 \\ 0 & 3 & 0 & | & -1 / 4 & 1/2 & 3/4 \\ 0 & 0 & 1 & | & 5/12 & 1/6 & -1/4 \ end {bmatrix} \] шаг 5 \ [ \красный цвет}{ \ begin {matrix} \\ (1/3) R_2 \\ \\ \ end {matrix}} \ begin {bmatrix} -2 & 2 & 0 & | & 1 & 0 & 0 \\ 0 & 1 & 0 & | & -1 / 12 & 1/6 & 1/4 \\ 0 & 0 & 1 & | & 5/12 & 1/6 & -1/4 \ end {bmatrix} \] шаг 6 \ [ \красный цвет}{ \ begin {matrix} R_1- 2 \ раз R_2 \\ \\ \\ \ end {matrix}} \ begin {bmatrix} -2 & 0 & 0 & | & 7/6 & -1 / 3 & -1 / 2 \\ 0 & 1 & 0 & | & -1 / 12 & 1/6 & 1/4 \\ 0 & 0 & 1 & | & 5/12 & 1/6 & -1/4 \ end {bmatrix} \] шаг 7 \ [ \красный цвет}{ \ begin {matrix} (-1/2) R_1 \\ \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 0 & 0 & | & -7 / 12 & 1/6 & 1/4 \\ 0 & 1 & 0 & | & -1 / 12 & 1/6 & 1/4 \\ 0 & 0 & 1 & | & 5/12 & 1/6 & -1/4 \ end {bmatrix} \] Следовательно \ [A ^ {- 1} = \ begin {bmatrix} -7 / 12 и 1/6 и 1/4 \\ -1 / 12 и 1/6 и 1/4 \\ 5/12 и 1/6 и -1/4 \ end {bmatrix} \]
Включены дополнительные примеры того, как найти обратную матрицу с помощью строковых операций. {th} \ ) столбец.Чтобы найти \ (M_ {1,1} \), удалите строку 1 и столбец 1 из матрицы A и найдите определитель оставшейся матрицы 2 на 2 следующим образом: \ (M_ {1,1} = Det \ begin {bmatrix} . &. &. \\ . & — 1 & 2 \\ . & 2 & 1 \ end {bmatrix} = -1 — 4 = -5 \)
Чтобы найти \ (M_ {1,2} \), удалите строку 1 и столбец 2 из матрицы A и найдите определитель оставшейся матрицы 2 на 2 следующим образом: \ (M_ {1,2} = Det \ begin {bmatrix} . &. &. \\ 2 &. & 2 \\ -1 &. & 1 \ end {bmatrix} = 2 — (- 2) = 4 \)
Чтобы найти \ (M_ {1,3} \), удалите строку 1 и столбец 3 из матрицы A и найдите определитель оставшейся матрицы 2 на 2 следующим образом: \ (M_ {1,3} = Det \ begin {bmatrix} .&. &. \\ 2 & -1 &. \\ -1 & 2 &. \ end {bmatrix} = 4 — 1 = 3 \)
Чтобы найти \ (M_ {2,1} \), удалите строку 2 и столбец 1 из матрицы A и найдите определитель оставшейся матрицы 2 на 2 следующим образом: \ (M_ {2,1} = Det \ begin {bmatrix} . & 0 & 1 \\ . &. &. \\ . & 2 & 1 \ end {bmatrix} = 0 — 2 = — 2 \)
. {- 1} = \ dfrac {1} {ad — bc} \ begin {bmatrix} d & -b \\ -c & a \\ \ end {bmatrix} \]Свойства обратных матриц
Матрица, имеющая обратную, называется обратимой матрицей.{-1} = А \)
Вопросы по обратным матрицам
- Вопрос 1
Используйте метод сокращения строк, чтобы найти инверсию следующих матриц:
\ (А = \ begin {bmatrix} -1 и -1 и 1 \\ 2 & 0 & -2 \\ 1 и 1 и 1 \ end {bmatrix} \) , \ (B = \ begin {bmatrix} 1 и 0 и 1 и 2 \\ -1 и 1 и 2 и 0 \\ -2 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \ end {bmatrix} \)- вопрос 2
Используйте метод сомножителей, чтобы найти обратную матрицу для следующей матрицы.
\ (А = \ begin {bmatrix} -1 & 0 & 3 \\ 3 и 2 и 2 \\ 0 и 0 и 1 \ end {bmatrix} \)- Вопрос 3
A, B и C — это матрицы 2 на 2. Матрицы B и C имеют следующий вид:
\ [B = \ begin {bmatrix} -1 & -1 \\ -2 и 1 \ end {bmatrix}, C = \ begin {bmatrix} 2 & -1 \\ -2 и 2 \ end {bmatrix} \] Найдите матрицу A такую, что AB = C.- Вопрос 4
Для какого значения k каждая из матриц, приведенных ниже, является обратимой?
а) \ ( \ begin {bmatrix} к & -1 & 4 \\ 2 & 0 & 1 \\ -1 & 0 & -1 \ end {bmatrix} \), б) \ (\ begin {bmatrix} к & -1 \\ -1 и 3 \ end {bmatrix} \), в) \ ( \ begin {bmatrix} к & -1 & 4 \\ 0 и к + 1 и 1 \\ 0 & 0 & k -3 \ end {bmatrix} \)- Вопрос 5
Квадратные матрицы P, Q, R и S имеют одинаковую размерность и обратимы, так что \ [P = Q R ^ {- 1} S \] Выразите (или определите) \ (R \) через \ (P \), \ (Q \) и \ (S \) или / и их обратные значения.- Вопрос 6
Матрица A определяется выражением
\ (А = \ begin {bmatrix} а & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & 0 \\ 0 и 0 и 0 и d \ end {bmatrix} \)
Найдите формулу, обратную матрице A, если ни один из параметров a, b, c и d не равен нулю.- Вопрос 7
Используйте обратную матрицу для решения системы уравнений \ ( \ begin {bmatrix} 1 и 0 и 1 и 2 \\ -1 и 1 и 2 и 0 \\ -2 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \ end {bmatrix} \ begin {bmatrix} x_1 \\ х_2 \\ х_3 \\ x_4 \ end {bmatrix} = \ begin {bmatrix} 0 \\ 1 \\ -1 \\ 2 \ end {bmatrix} \)- Вопрос 8
Какой метод является наиболее эффективным для решения следующих систем уравнений?
\ (A X_1 = B_1 \), \ (A X_2 = B_2 \), \ (A X_3 = B_3 \).{-1} = А В \).
Найдите B в терминах A или обратного.- Вопрос 10
1) Приведите пример матриц 2 на 2 A и B, таких, что ни A, ни B не обратимы, но A + B обратимы.
2) Приведите пример матриц 2 на 2 A и B, таких, что ни A, ни B не обратимы, но A — B обратимы.- Вопрос 11
Используйте любой из двух методов, чтобы найти формулу, обратную матрице 2 на 2. (она уже приведена выше без доказательства).- Вопрос 12
Система уравнений в матричной форме
\ (А Х = В \)
имеет следующие решения: \ (X_1 = \ begin {bmatrix} -1 \\ 2 \\ 3 \ end {bmatrix} \) для \ (B_1 = \ begin {bmatrix} 2 \\ 13 \\ 3 \ end {bmatrix} \), \ (X_2 = \ begin {bmatrix} 0 \\ -1 \\ 1 \ end {bmatrix} \) для \ (B_2 = \ begin {bmatrix} 4 \\ 2 \\ 2 \ end {bmatrix} \), \ (X_3 = \ begin {bmatrix} 1 \\ 1 \\ 1 \ end {bmatrix} \) для \ (B_3 = \ begin {bmatrix} 4 \\ 5 \\ 3 \ end {bmatrix} \).
Найдите X для \ (B = \ begin {bmatrix} 1 \\ -9 \\ -1 \ end {bmatrix} \).Решения вышеперечисленных вопросов
- Решение вопроса 1
Обратная матрица A
Запишите расширенную матрицу \ ([A | I) \) \ [\ begin {bmatrix} -1 & -1 & 1 & | & 1 & 0 & 0 \\ 2 & 0 & -2 & | & 0 & 1 & 0 \\ 1 & 1 & 1 & | & 0 & 0 & 1 \ end {bmatrix} \]
шаг 1 \ [ \ color {red} {\ begin {matrix} -R_1 \\ \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 1 & -1 & | & -1 & 0 & 0 \\ 2 & 0 & -2 & | & 0 & 1 & 0 \\ 1 & 1 & 1 & | & 0 & 0 & 1 \ end {bmatrix} \]
шаг 2 \ [ \ color {red} {\ begin {matrix} \\ R_2-2R_1 \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 1 & -1 & | & -1 & 0 & 0 \\ 0 & -2 & 0 & | & 2 & 1 & 0 \\ 1 & 1 & 1 & | & 0 & 0 & 1 \ end {bmatrix} \]
шаг 3 \ [ \ color {red} {\ begin {matrix} \\ \\ R_3-R_1 \\ \ end {matrix}} \ begin {bmatrix} 1 & 1 & -1 & | & -1 & 0 & 0 \\ 0 & -2 & 0 & | & 2 & 1 & 0 \\ 0 & 0 & 2 & | & 1 & 0 & 1 \ end {bmatrix} \]
шаг 4 \ [ \ color {red} {\ begin {matrix} \\ R_2 = (- 1/2) R_2 \\ R_3 = (1/2) R_3 \\ \ end {matrix}} \ begin {bmatrix} 1 & 1 & -1 & | & -1 & 0 & 0 \\ 0 & 1 & 0 & | & -1 & -1 / 2 & 0 \\ 0 & 0 & 1 & | & 1/2 & 0 & 1/2 \ end {bmatrix} \]
шаг 5 \ [ \ color {red} {\ begin {matrix} R_1 + R_3 \\ \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 1 & 0 & | & -1 / 2 & 0 & 1/2 \\ 0 & 1 & 0 & | & -1 & -1 / 2 & 0 \\ 0 & 0 & 1 & | & 1/2 & 0 & 1/2 \ end {bmatrix} \]
шаг 6 \ [ \ color {red} {\ begin {matrix} R_1-R_2 \\ \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 0 & 0 & | & 1/2 & 1/2 & 1/2 \\ 0 & 1 & 0 & | & -1 & -1 / 2 & 0 \\ 0 & 0 & 1 & | & 1/2 & 0 & 1/2 \ end {bmatrix} \]
Матрица, обратная матрице A, — это матрица 3 на 3 справа.{-1} = \ begin {bmatrix} 1/2 и 1/2 и 1/2 \\ -1 и -1 / 2 и 0 \\ 1/2 и 0 и 1/2 \ end {bmatrix} \]Обратная матрица B
Запишите расширенную матрицу \ ([A | I) \) \ [\ begin {bmatrix} 1 & 0 & 1 & 2 & | & 1 & 0 & 0 & 0 \\ -1 & 1 & 2 & 0 & | & 0 & 1 & 0 & 0 \\ -2 & 0 & 1 & 2 & | & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & | & 0 & 0 & 0 & 1 \ end {bmatrix} \]
шаг 1 \ [ \ color {red} {\ begin {matrix} \\ R_2 + R_1 \\ R_3 + 2R_1 \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 0 & 1 & 2 & | & 1 & 0 & 0 & 0 \\ 0 & 1 & 3 & 2 & | & 1 & 1 & 0 & 0 \\ 0 & 0 & 3 & 6 & | & 2 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & | & 0 & 0 & 0 & 1 \ end {bmatrix} \]шаг 2 \ [ \ color {red} {\ begin {matrix} \\ \\ (1/3) R_3 \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 0 & 1 & 2 & | & 1 & 0 & 0 & 0 \\ 0 & 1 & 3 & 2 & | & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 2 & | & 2/3 & 0 & 1/3 & 0 \\ 0 & 0 & 0 & 1 & | & 0 & 0 & 0 & 1 \ end {bmatrix} \]
шаг 3 \ [ \ color {red} {\ begin {matrix} R_1-2R_4 \\ Р_2-2Р_4 \\ Р_3-2Р_4 \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 0 & 1 & 0 & | & 1 & 0 & 0 & -2 \\ 0 & 1 & 3 & 0 & | & 1 & 1 & 0 & -2 \\ 0 & 0 & 1 & 0 & | & 2/3 & 0 & 1/3 & -2 \\ 0 & 0 & 0 & 1 & | & 0 & 0 & 0 & 1 \ end {bmatrix} \]
шаг 4 \ [ \ color {red} {\ begin {matrix} R_1-R_3 \\ Р_2-3Р_3 \\ \\ \\ \ end {matrix}} \ begin {bmatrix} 1 & 0 & 1 & 0 & | & 1/3 & 0 & -1 / 3 & 0 \\ 0 & 1 & 0 & 0 & | & -1 & 1 & -1 & 4 \\ 0 & 0 & 1 & 0 & | & 2/3 & 0 & 1/3 & -2 \\ 0 & 0 & 0 & 1 & | & 0 & 0 & 0 & 1 \ end {bmatrix} \]
Матрица, обратная матрице B, — это матрица 4 на 4 справа.{-1} = \ begin {bmatrix} 1/3 и 0 и -1 / 3 и 0 \\ -1 и 1 и -1 и 4 \\ 2/3 и 0 и 1/3 и -2 \\ 0 & 0 & 0 & 1 \ end {bmatrix} \]- Решение вопроса 2
Сначала находим несовершеннолетних.
\ (M_ {1,1} = Det \ begin {bmatrix} . &. &. \\ . & 2 & 2 \\ . & 0 & 1 \ end {bmatrix} = 2 \), \ (M_ {1,2} = Det \ begin {bmatrix} . &. &. \\ 3 &. & 2 \\ 0 &. & 1 \ end {bmatrix} = 3 \), \ (M_ {1,3} = Det \ begin {bmatrix} . &. &. \\ 3 и 2 и.\\ 0 & 0 &. \ end {bmatrix} = 0 \)\ (M_ {2,1} = Det \ begin {bmatrix} . & 0 & 3 \\ . &. &. \\ . & 0 & 1 \ end {bmatrix} = 0 \), \ (M_ {2,2} = Det \ begin {bmatrix} -1 &. & 3 \\ . &. &. \\ 0 &. & 1 \ end {bmatrix} = -1 \), \ (M_ {2,3} = Det \ begin {bmatrix} -1 & 0 &. \\ . &. &. \\ 0 & 0 &. \ end {bmatrix} = 0 \)
\ (M_ {3,1} = Det \ begin {bmatrix} . & 0 & 3 \\ . & 2 & 2 \\ . &. &. \ end {bmatrix} = — 6 \), \ (M_ {3,2} = Det \ begin {bmatrix} -1 &.{-1} = \ begin {bmatrix} 2 & -1 \\ -2 и 2 \ end {bmatrix} (- \ dfrac {1} {3}) \ begin {bmatrix} 1 и 1 \\ 2 и -1 \ end {bmatrix} = \ begin {bmatrix} 0 & -1 \\ -2/3 и 4/3 \ end {bmatrix} \)
Примечание: вы можете проверить ответ для матрицы A, подставив в уравнение \ (A B = C \)
- Решение вопроса 4
Матрица обратима, если ее определитель не равен нулю.
a) Используя второй столбец,
Дет \ ( \ begin {bmatrix} к & -1 & 4 \\ 2 & 0 & 1 \\ -1 & 0 & -1 \ end {bmatrix} = — 1 \) Матрица обратима для любых k вещественныхб) Дет \ (\ begin {bmatrix} к & -1 \\ -1 и 3 \ end {bmatrix} = 3k — 1 \)
\ (3k — 1 \ ne 0 \)
\ (к \ нэ 1/3 \)
Матрица в части b) обратима для всех действительных значений k, не равных 1/3.{-1} Q \)- Решение вопроса 6
Запишите расширенную матрицу \ ([A | I] \)\ (\ begin {bmatrix} a & 0 & 0 & 0 & | & 1 & 0 & 0 & 0 \\ 0 & b & 0 & 0 & | & 0 & 1 & 0 & 0 \\ 0 & 0 & c & 0 & | & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & d & | & 0 & 0 & 0 & 1 \ end {bmatrix} \)
Умножьте строку (1) на 1 / a, строку (2) на 1 / b, строку (3) на 1 / c и строку (4) на 1 / d и упростите
\ (\ begin {bmatrix} 1 & 0 & 0 & 0 & | & 1 / a & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & | & 0 & 1 / b & 0 & 0 \\ 0 & 0 & 1 & 0 & | & 0 & 0 & 1 / c & 0 \\ 0 & 0 & 0 & 1 & | & 0 & 0 & 0 & 1 / d \ end {bmatrix} \)
Обратная матрица имеет вид
\ (A ^ {- 1} = \ begin {bmatrix} 1 / а & 0 & 0 & 0 \\ 0 & 1 / b & 0 & 0 \\ 0 & 0 & 1 / c & 0 \\ 0 & 0 & 0 & 1 / д \ end {bmatrix} \)
- Решение вопроса 7
Система имеет вид
A X = B с A = \ ( \ begin {bmatrix} 1 и 0 и 1 и 2 \\ -1 и 1 и 2 и 0 \\ -2 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \ end {bmatrix} \), \ (B = \ begin {bmatrix} 0 \\ 1 \\ -1 \\ 2 \ end {bmatrix} \) и \ (X = \ begin {bmatrix} x_1 \\ х_2 \\ х_3 \\ x_4 \ end {bmatrix} \)
Справа Умножьте обе части уравнения на \ (A ^ {- 1} \) и упростите.{-1} B = \ begin {bmatrix} 1/3 & 0 & -1 / 3 & 0 \\ -1 и 1 и -1 и 4 \\ 2/3 и 0 и 1/3 и -2 \\ 0 & 0 & 0 & 1 \ end {bmatrix} \ begin {bmatrix} 0 \\ 1 \\ -1 \\ 2 \ end {bmatrix} = \ begin {bmatrix} \ dfrac {1} {3} \\ 10 \\ — \ dfrac {13} {3} \\ 2 \ end {bmatrix} \)- Решение вопроса 8
Поскольку матрица A является общей для всех данных систем, наиболее эффективный метод решения систем уравнений вида
\ (A X_1 = B_1 \), \ (A X_2 = B_2 \), \ (A X_3 = B_3 \).{-2} \)- Решение вопроса 10
Есть много возможных ответов на обе части этого вопроса.
1) \ (A = \ begin {bmatrix} 1 & 1 \\ 0 & 0 \\ \ end {bmatrix}, B = \ begin {bmatrix} 0 & 0 \\ — 1 & 1 \\ \ end {bmatrix} \), \ (A + B = \ begin {bmatrix} 1 & 1 \\ — 1 & 0 \\ \ end {bmatrix} \)2) \ (A = \ begin {bmatrix} 3 & 1 \\ 0 & 0 \\ \ end {bmatrix}, B = \ begin {bmatrix} 0 & 0 \\ — 1 и 4 \\ \ end {bmatrix} \), \ (A — B = \ begin {bmatrix} 3 & 1 \\ 1 & — 4 \\ \ end {bmatrix} \)
Проверить, что определитель матриц A и B равен нулю и, следовательно, необратим.

 {-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе. {-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}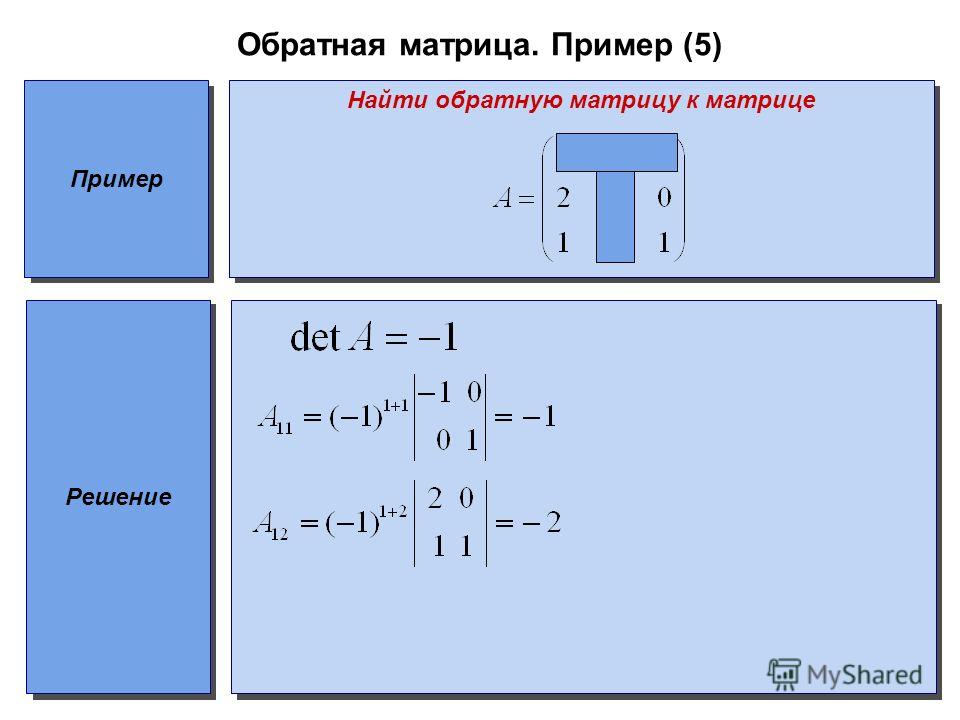 {-1} = \frac{1}{\det(\mathbf{A})} \begin& \!\!-b \\ -c & \,a \\ \end{bmatrix} = \frac{1}{ad — bc} \begin{bmatrix} \,\,\,d & \!\!-b\\ -c & \,a \\ \end{bmatrix}.}
{-1} = \frac{1}{\det(\mathbf{A})} \begin& \!\!-b \\ -c & \,a \\ \end{bmatrix} = \frac{1}{ad — bc} \begin{bmatrix} \,\,\,d & \!\!-b\\ -c & \,a \\ \end{bmatrix}.} Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн
Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.
Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде. Обратная матрица может существовать только для квадратных матриц.
Обратная матрица может существовать только для квадратных матриц. Результирующая матрица является обратной для исходной матрицы.
Результирующая матрица является обратной для исходной матрицы.

 1.
1. -1 = (» adj «A) / (detA)`
-1 = (» adj «A) / (detA)` -1 = 1 / (| A |) ((2,2), (6,7))`
-1 = 1 / (| A |) ((2,2), (6,7))` {- 1} \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right) = \ left ( \ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right) \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right) = \ left (\ begin {array} {c} 1 \\ — 2 \\ 2 \ end {array} \ right).
{- 1} \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right) = \ left ( \ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right) \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right) = \ left (\ begin {array} {c} 1 \\ — 2 \\ 2 \ end {array} \ right).