Численные и вычислительные методы, оптимизация
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| klubni4ka |
| ||
11/01/12 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| мат-ламер |
| |||
30/01/09 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Aleksandr Pavlovich |
| ||
05/05/12 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| fit |
| ||
07/03/10 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| AndrewN |
| ||
13/01/12 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| TOTAL |
| |||
23/08/07 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 11 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Обратная матрица — презентация онлайн
Похожие презентации:
Матрицы и определители
Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения
Невырожденные матрицы. Обратная матрица. Матричные уравнения
Определитель и его свойства. Обратная матрица
Обратная матрица. (Тема 7)
Матрицы и определители
Матрицы, определители. Обратная матрица. Ранг матрицы. Системы линейных уравнений элементы векторной алгебры
Обратная матрица
Линейная алгебра. Матрицы и действия над ними
Высшая математика. Лекция 2. Обратная матрица
Матрицы и СЛАУ МНК. (Лекция 5 )
1. Обратная Матрица
2. Определение. Матрица называется о б р а т н о й к квадратной матрице , если
A B B A EОбратная матрица обозначается символом
1
1
A
1
A A A A E
Примечание. Операция деления для матриц не
определена. Вместо этого предусмотрена операция
обращения (нахождения обратной) матрицы.
3. Определение. Матрица, составленная из алгебраических дополнений для элементов исходной матрицы , называется с о ю з н о й м а т р и ц е й .
Определение. Матрица, составленная из
Матрица, составленная изалгебраических дополнений для элементов
исходной матрицы , называется
союзной матрицей.
A11
A A21
A
31
A12
A22
A32
A13
A23
A33
4. Формула для нахождения обратной матрицы
11
T
A
A
det A
A11 A21 A31
1
1
A
A12 A22 A32
det A
A
A
A
13 23 33
6. Алгоритм нахождения
• 1. Находим определительматрицы А. Он должен быть
отличен от нуля.
• 2. Находим алгебраические
дополнения для каждого
элемента матрицы А.
• 3. Составляем союзную
матрицу и транспонируем ее.
• 4. Подставляем результаты
п.1 и п.4 в формулу обратной
матрицы.
A
1
7. Пример. Найти матрицу, обратную к матрице:
1 2A
4
3
Р е ш е н и е. Действуем по алгоритму:
1. Находим определитель матрицы:
1 2
det A =
3 4
= 4- 6 = — 2
Определитель отличен от нуля det A № 0 ,
следовательно, обратная матрица существует.

2. Находим алгебраические дополнения:
A11 = 4
A21 = — 2
A12 = — 3
A22 = 1
3. Составляем союзную матрицу:
~ 4 3
A
2 1
4. Записываем обратную матрицу по
формуле
1
T
1 4
A
A
2 3
det A
1
2
1
13. 5. Проверка
• Воспользуемся определением обратнойматрицы и найдем произведение
1
A A
1 4 2 1 2
2 3 1 3 4
1 4 1 2 3 4 2 2 4 1 2 0 1 0
2 0 2 0 1
2 3 1 1 3 3 2 1 4
14. Задача. Найти матрицу, обратную к данной
2 1 1A 3 2 1
1 2 1
15. 1. Находим определитель
2 1 1det A 3 2 1 2 2 1 3 2 1 1 1 1
1 2 1
1 2 1 1 2 2 3 1 1
4 6 1 2 4 3 3 5 2 0.
16. 2. Алгебраические дополнения для первой строки:
2 1A11
2 2 4,
2 1
3 1
A12
3 1 2,
1 1
3 2
A13
6 2 8,
1 2
17. Алгебраические дополнения для второй строки:
1 1A21
1 2 1,
2 1
2 1
A22
2 1 1,
1 1
2 1
A23
4 1 3,
1 2
18.
 Алгебраические дополнения для третьей строки:1 1
Алгебраические дополнения для третьей строки:1 1A31
1 2 3,
2 1
2 1
A32
2 3 1,
3 1
2 1
A33
4 3 7.
3 2
19. Обратная матрица:
4 1 31
1
A 2 1 1
2
8
3
7
20. Элементарные преобразования матриц
• перестановка строк (столбцов) местами;• исключение из матрицы строк (столбцов),
состоящих из нулей;
• умножение всех элементов какой-либо строки
(столбца) матрицы на любое число, отличное от
нуля;
• прибавление к одной строке (столбцу) другой,
предварительно умноженной на любое число,
отличное от нуля.
Определение. Э к в и в а л е н т н ы м и называются
матрицы, полученные одна из другой путем элементарных
преобразований.
Важным понятием для матриц является понятие РАНГА.
Существует несколько определений этого понятия. Мы
остановимся на одном из них, основанном на элементарных
преобразованиях.
Определение. Р а н г о м м а т р и ц ы называется
число ненулевых строк в матрице, после приведения ее к
ступенчатому виду (путем элементарных преобразований).

Обозначение. Ранг матрицы будем обозначать r ( A)
или
rang ( A)
.
Теорема. Ранг матрицы не меняется при элементарных
преобразованиях.
English Русский Правила
Найти обратную матрицу с помощью Python | Эндрю Джозеф Дэвис
Как найти обратную матрицу с помощью операций со строками в Python
Введение
Эта статья следует за « Алгоритм исключения Гаусса в Python» . В нем представлен метод нахождения обратной матрицы с использованием редукции строк.
Ознакомьтесь со статьей ниже, чтобы получить необходимые сведения об исключении Гаусса.
Алгоритм исключения Гаусса в Python
Учебник по решению системы линейных уравнений методом исключения Гаусса в Python
levelup.gitconnected.com
Photo by Linus Mimietz on UnsplashBackground
“ Основы матричной алгебры | Часть 2 » представляет обратных матриц . Напомним, что не все матрицы обратимы.0010 .
Напомним, что не все матрицы обратимы.0010 .
Основы матричной алгебры в Python | Часть 2
Понимание и реализация основных концепций и операций матричной алгебры с Python
в направлении datascience.com
По существу, умножение матрицы на ее обратную дает Identity Matrix, обозначенную как 901 0, , Уравнение 1.
Уравнение 1 — Вычисление обратной матрицы (изображение автора)Возьмем матрицу 3×3 A в уравнении 2 в качестве примера.
Уравнение 2 — Матрица A (изображение автора)Уравнение 3 эквивалентно уравнению 1 с переменными , замененными на .
Уравнение 3 — Подстановка параметров (изображение автора)Результатом следующего вычисления является неизвестное A⁻¹ .
Алгоритм
Создайте расширенную матрицу из компонентов уравнения 3. Эта новая матрица содержит A CONCATENATED С точки зрения колонны с I , как в уравнении 4.
дополненная матрица .
Выполнение исключения Гаусса тип процедуры на расширенной матрице для получения A в сокращенная форма эшелона строк ( rref ) одновременные переходы I в A ⁻¹ .
Итого:
- Преобразование A в rref . Таким образом, A становится единичной матрицей .
- Выполните эквивалентных операций со строками выше на I , что станет обратной матрицей А ⁻¹.
Пример
На рис. 1 показаны пошаговых операций , необходимых для изменения первых трех столбцов расширенной матрицы для получения 1 rref .
Результат соответствует ожидаемому. A становится идентификационной матрицей , а I преобразуется в ранее неизвестную обратную матрицу .
Реализация Python
Имея запрограммированный алгоритм исключения Гаусса в Python, код требует только незначительных модификаций для получения обратного .
Определить A из уравнения 2 как массив NumPy с использованием Gist 1.
Gist 1 — определить A с помощью NumpyАналогично, создать экземпляр новой переменной I , который имеет ту же квадратную форму , что и A .
Суть 2 — Определение матрицы идентичности Создание расширенной матрицы с использованием операции NumPy конкатенации по столбцам, как указано в Gist 3.
Без учета определенных пограничных случаев приведенный ниже в Gist 4 представляет собой наивную реализацию операций со строками, необходимых для получения Инверсия .
Gist 4 — Найти обратную матрицу в PythonПо сравнению с алгоритмом исключения Гаусса, первичная модификация кода состоит в том, что вместо из завершается на строке-эшелоне формы , операции продолжают прибывать к сокращенной строке эшелонированная форма .
Следовательно, вместо итерации исключительно ниже опорной точки, строк над опорной точкой также проходятся и обрабатываются .
Выполнение 9Скрипт 0009 возвращает тот же ответ, что и на рисунке 1.
Рисунок 2. Вывод консоли Python с обратной матрицей Также возможно увеличение размера матрицы. Gist 5 предоставляет код для создания случайной квадратной матрицы в NumPy.
Сравнение среды выполнения с пользовательской 9Алгоритм 0010 по сравнению с эквивалент NumPy подчеркивает разницу в скорости . Код в Gist 6 представляет собой простой способ записи таймингов .
Суть 6 — Сравните время выполнения методаNumPy на быстрее на секунду, чтобы инвертировать матрицу. Эта колоссальная разница во времени будет только увеличиваться по мере расширения размеров матрицы.
Заключение
В этой статье изложен основной метод, используемый в матричной алгебре с по вычислить обратную матрицу.
Используйте описанный метод теоретической матричной алгебры и эквивалентный код Python , чтобы понять, как работает операция . Однако такие библиотеки, как NumPy в Python, оптимизированы для эффективного расшифровки обратных матриц. На практике используйте надежные, хорошо поддерживаемые математические библиотеки.
Ознакомьтесь с другими моими статьями, если вы интересуетесь Python, инженерией и наукой о данных.
Присоединяйтесь к Medium по моей реферальной ссылке — Эндрю Джозеф Дэвис
Как участник Medium, часть вашего членского взноса идет авторам, которых вы читаете, и вы получаете полный доступ ко всем историям…
medium.com
Найдите весь код Python в Gist 7.
Gist 7 — Полный код Python для поиска обратной матрицыСсылки
[1] Алгебра матриц для инженеров — Джеффри Р. Часнов
14. Обратная матрица и правило Крамера
Преподавание, линейная алгебра и геометрия I UW
м_корч
Проблемы, решения.
Теперь воспользуемся определителями и попутно введем понятие обратной матрицы.
Обратная матрица
Матрица обратна матрице , если , где – единичная матрица (матрица с единицами по диагонали и нулями везде). Обратная матрица обозначается как . Поскольку и , мы видим, что . Это означает, что только матрицы с ненулевыми определителями могут иметь свои обратные. Поэтому мы называем такие матрицы обратимыми.
Обратная матрица обозначается как . Поскольку и , мы видим, что . Это означает, что только матрицы с ненулевыми определителями могут иметь свои обратные. Поэтому мы называем такие матрицы обратимыми.
Как вычислить обратную заданную матрицу? Недавно мы упоминали, что операции над строками матрицы, приводящие к уменьшенной «ступенчатости» for, на самом деле являются умножением на матрицу. Представьте, что мы преобразуем матрицу, состоящую из матрицы вместе с единичной матрицей, в редуцированную «ступенчатую» форму. Так как это квадратная матрица с ненулевым определителем, мы получим единичную матрицу в левой части: . Но заметьте, что если это матрица операций со строками, то . Поэтому и . Из первого уравнения следует, что . Второй то. Таким образом, мы получаем обратную матрицу справа после этих операций!
Напр. вычислим обратную следующую матрицу:
Итак:
И поэтому:
Определение одного элемента обратной матрицы
Если вам нужна не вся матрица, а только некоторые элементы, следующий способ кажется полезным. Он использует сопряженную матрицу к заданной. Сопряженная матрица — это матрица, в которой в -й строке и -м столбце стоит определитель матрицы (матрица без -й строки и -го столбца, здесь нет ошибки, здесь играет роль перестановка), умноженная на . Выполняется следующее равенство:
Он использует сопряженную матрицу к заданной. Сопряженная матрица — это матрица, в которой в -й строке и -м столбце стоит определитель матрицы (матрица без -й строки и -го столбца, здесь нет ошибки, здесь играет роль перестановка), умноженная на . Выполняется следующее равенство:
Следовательно, если мы хотим вычислить значение во второй строке и первом столбце из предыдущего примера, мы вычеркнем второй столбец и первую строку и вычислим определители, и получим:
что согласуется с результатом, полученным первым методом!
Правило Крамера
Имея систему уравнений с переменными, мы можем попытаться решить ее с помощью правила Крамера. Пусть – матрица этой системы без столбца свободных коэффициентов. Пусть – матрица , в которой вместо -го столбца поставлен столбец свободных коэффициентов. Тогда:
- если система имеет ровно одно решение. Решение находится по следующей формуле: ,
- если , и хотя бы одно из не равно , система не имеет решений,
- если и для каждого , может быть ноль или бесконечно много решений — метод Крамера не дает точного ответа.


 01.2012, 19:14
01.2012, 19:14 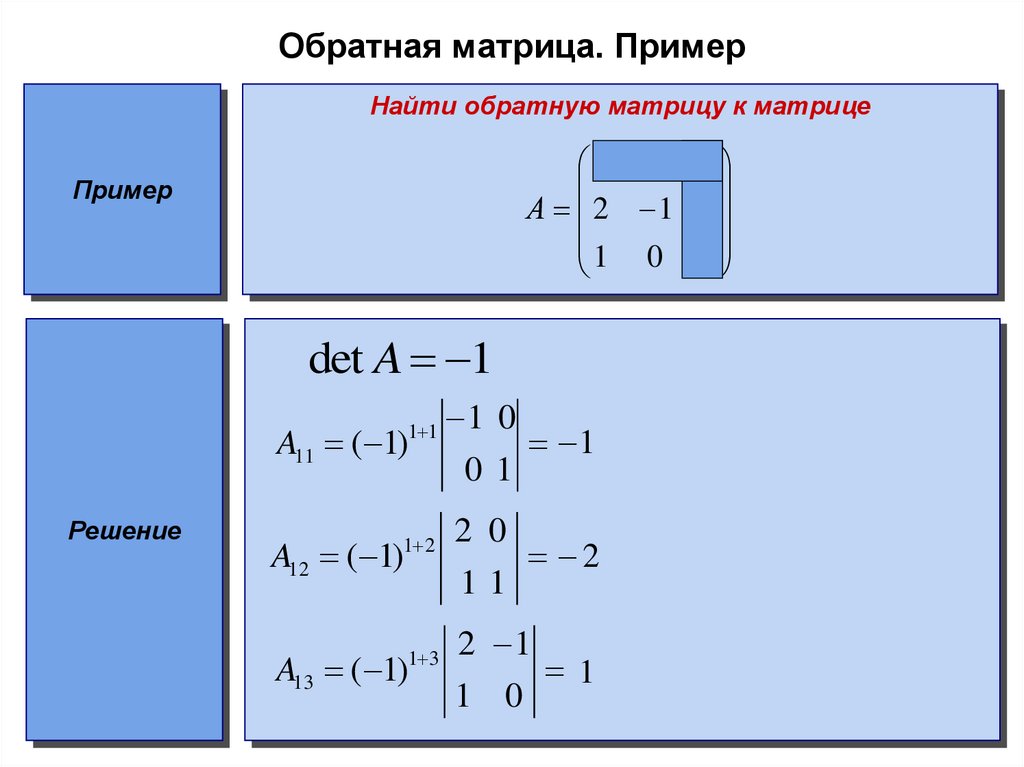 01.2012, 20:09
01.2012, 20:09  01.2012, 08:49
01.2012, 08:49  05.2012, 10:54
05.2012, 10:54  05.2012, 17:44
05.2012, 17:44  06.2012, 02:02
06.2012, 02:02  06.2012, 10:02
06.2012, 10:02  Но не принципиально эффективнее — всего раза в полтора, кажется.
Но не принципиально эффективнее — всего раза в полтора, кажется. Разница лишь в нюансах.
Разница лишь в нюансах.