Нахождение производной с помощью производной: Нахождение производной

Алгоритм нахождения производной функции. Алгебра 10-11 класс Мордкович. – Рамблер/класс

Алгоритм нахождения производной функции. Алгебра 10-11 класс Мордкович. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Кто знает алгоритм нахождения производной функции у = f(х)?
 

ответы

Алгоритм нахождения производной

функции у = f(х).
 
1. Зафиксировать значение х, найти f(x).
2. Дать аргументу х приращение Ах, перейти в новую точку х + ∆х, найти f(x + ∆х).
3. Найти приращение функции: ∆ у = f(х + ∆х) — f(х).
4. Составить отношение 
5. Вычислить 
Этот предел и есть f(x).
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

9 класс

похожие вопросы 5

ГДЗ по геометрии 8 класс Атанасян. Гл.V №441. Докажите, что прямые,….

Не понимаю, как решить задачу Гл.V №441.
Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.
  (Подробнее…)

11 класс8 классГеометрияАтанасян Л.С.

№ 59. 8 ГДЗ Алгебра 10-11 класс Мордкович. Сколько решений имеет система уравнений?

Применяя графический метод, определите, сколько решений имеет система уравнений: (Подробнее…)

ГДЗАлгебра10 класс11 классМордкович А.Г.

Решите систему уравнений. Поможете? № 59.21 ГДЗ Алгебра 10-11 класс Мордкович.

Решите систему уравнений: (Подробнее…)

ГДЗАлгебра10 класс11 классМордкович А.Г.

№ 11.15 ГДЗ Алгебра 10-11 класс Мордкович. Сколько решений имеет система уравнений?

Помогите определить!
Сколько решений имеет система уравнений: (Подробнее…)

ГДЗАлгебра10 класс11 классМордкович А.Г.

Хелп № 1117 ГДЗ Геометрия 9 класс Атанасян Л.С.

Найдите площадь круга, вписанного: а) в равносторонний треугольник со стороной а; б) в прямоугольный треугольник с катетом а и (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

8.

Производная. Правила дифференцирования. Таблица производных, Производная сложных функций. Исследование функции с помощью производной.

Определение: производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента при (если такой предел существует):

.

Геометрический смысл производной.

Производная в точке равна угловому коэффициенту касательной к графику функции в этой точке.

ч

Уравнение касательной к графику функции в точке :

.

Правила нахождения производной.

Если у функций и существуют производные, то

Производная сложной функции.

Если и существуют производные и , то , где индексы и указывают, по какому аргументу берутся производные.

Производные элементарных функций.

Пример. Вычислить производную функции .

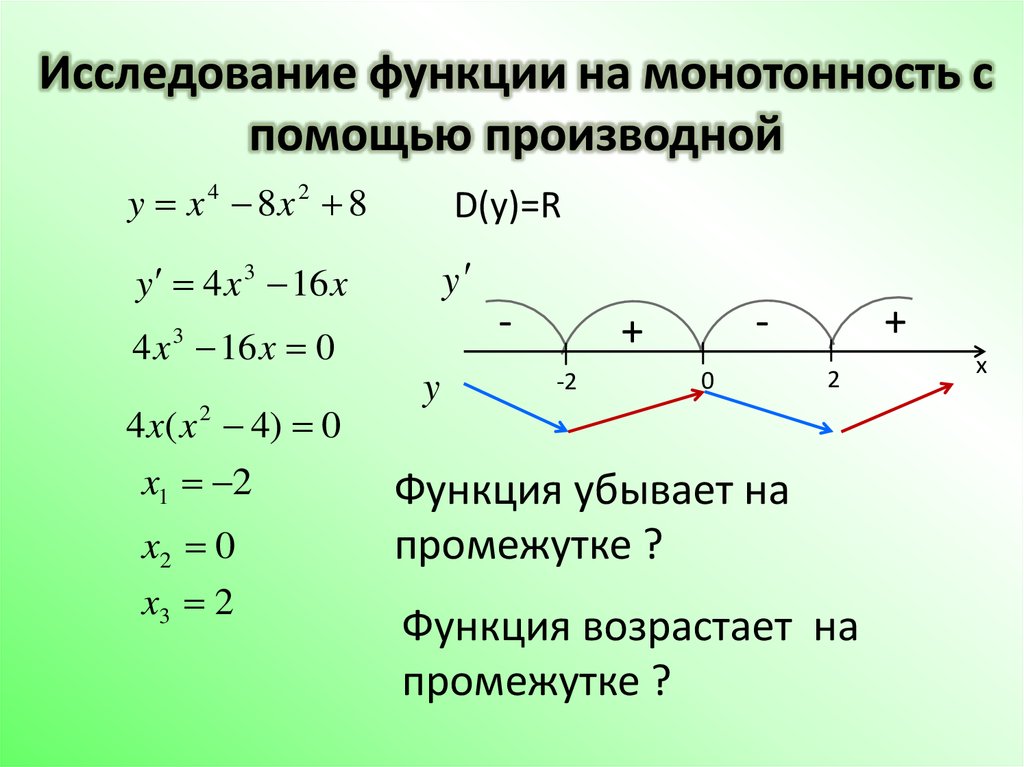
Исследование функции с помощью производной.

1. Монотонность

Достаточное условие возрастания функции

Если в каждой точке интервала , то функция возрастает на этом интервале.

Достаточное условие убывания функции

Если в каждой точке интервала , то функция убывает на этом интервале.

2. Экстремумы

Определение. Точка называется точкой минимума функции , если для всех из некоторой окрестности точки выполнено неравенство .

Определение. Точка называется точкой максимума функции , если для всех из некоторой окрестности точки выполнено неравенство .

Для точек максимума и минимума функции принято общее название – точки экстремума функции. Значения в этих точках называют соответственно максимумами ( ) и минимумами ( ) функции.

Необходимое условие экстремума функции

Для того, чтобы функция имела экстремум в точке , необходимо, чтобы производная в этой точке равнялась нулю ( ) или не существовала.

Точки, в которых выполнено необходимое условие экстремума, то есть производная равна нулю или не существует, называются критическими точками. Отметим, что эти точки должны входить в область определения функции.

Таким образом, если в какой-то точке имеется экстремум, то эта точка критическая. Однако, обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума.

Достаточное условие экстремума функции

Если при переходе через точку производная дифференцируемой функции меняет свой знак с плюса на минус, то точка есть точка максимума функции , а если с минуса на плюс, то точка минимума.

Схема нахождения интервалов монотонности и экстремумов функции

1. Найти область определения функции.

2. Найти производную функции.

3. Найти критические точки.

4. В каждом из интервалов, а которые область определения разбивается критическими точками, определить знак производной и характер изменения функции.

5. Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума.

6. Записать результат исследования функции: промежутки монотонности и экстремумы.

Что такое производная? Производные Определение и значение

Explore Derivatives

Если у вас есть вопросы о деривативах — например, что это такое, почему они используются и как их найти — вы обратились по адресу! Производные являются фундаментальной концепцией в вашем путешествии по исчислению, поэтому не стесняйтесь потратить на это некоторое время.

Мы не хотим переусердствовать, но мы думаем, что вы извлечете большую пользу из приведенных ниже деталей (извините, нам пришлось).

Впрочем, хватит шуток! Время сосредоточиться на наших сильных сторонах.

Давайте научимся математике, ладно?

Что такое производная?

Производная — один из важнейших инструментов дифференциального исчисления. Производные дают нам гибкий способ измерения точных скоростей изменений, что действительно здорово!

Вы можете использовать производные во многих различных сценариях, включая:

• Производные функции
• Производные выражения
• Производные интегралов
• Первые производные и вторые производные
• Производные высшего порядка

Значение производных

Проще говоря, производные показывают нам мгновенную скорость изменения в конкретной точке на графике функции. Это означает, что мы можем с относительной легкостью получить довольно надежную информацию (в зависимости от уровня вычислений, которые вы выполняете!).

Кроме того, возможность находить производные дает нам возможность более точно моделировать такие вещи, как скорость, сила, ускорение и т. д., поэтому они используются не только для того, чтобы бросить вам вызов во время выполнения домашних заданий. Производные на самом деле имеют решающее значение для внутренней работы очень многих вещей вокруг нас.

Например: допустим, вы находитесь на бейсбольном матче и хотите узнать скорость изменения скорости мяча, когда он покидает руку питчера. В этом случае вы захотите взять производную!

Производная и наклон

Трудно говорить о производных, не связывая их с наклоном.

Почему? Потому что нахождение производной на самом деле эквивалентно нахождению наклона касательной в определенной точке функции.

Забавный факт: то, как мы вычисляем производную, зависит от того, как мы вычисляем наклон! Это подъем над пробегом, но с несколькими интересными поворотами.

Определение производной

Итак, зная контекст производных и то, что они нам говорят, как мы определяем «производную»? Вот наше определение:

Производная : ( n ) скорость изменения величины по отношению к изменению переменной; результат дифференцирования

Достаточно просто, правда?

Производные в математике и деривативы в финансах

Для ясности: мы здесь, чтобы рассказать вам о деривативах в математике, но вы также можете найти информацию о деривативах в финансах или инвестициях.

Если это то, что вы ищете, вам следует знать, что «дериватив» в финансах — это контракт, стоимость которого определяется динамикой актива, процентной ставкой или другим «базовым активом».

Но мы здесь, чтобы учить математику, так что давайте займемся уравнениями!

Как будут выглядеть уравнения с производными?

Мы можем говорить о «почему» деривативов до посинения, но теперь пришло время сосредоточиться на «как» и посмотреть, как деривативы будут выглядеть на странице. 92}$$

Примечание. Это всего лишь примеры, а НЕ решения этих проблем!

Пока вы работаете с этими уравнениями, не забывайте о правилах дифференцирования, которые помогут вам более стратегически управлять вычислениями!

Постоянная кратность производных	$$\frac{d}{dx}\left(c\times f(x)\right)=c\times\frac{d}{dx}\left(f(x) \right)$$
Правило сумм для производных	$$\frac{d}{dx}\left(f(x) + g(x)\right)=\frac{d}{dx}\left( f(x) \right)+\frac{d }{dx}\left( g(x) \right)$$
Правило разности для производных	$$\frac{d}{dx}\left(f(x) — g(x)\right)=\frac{d}{dx}\left( f(x) \right)-\frac{d }{dx}\left( g(x) \right)$$
Правило произведения для производных	$$\frac{d}{dx}\left(f(x)\times g(x)\right)=\frac{d}{dx}\left( f(x) \right)\times g( x)+f(x)\times\frac{d}{dx}\left( g(x) \right) $$
Частное правило для производных	$ $ \ frac {d} {dx} \ left (\ frac {f (x)} {g (x)} \ right) = \ frac {\ frac {d} {dx} \ left (f (x) \right)\times g(x)-f(x)\times\frac{d}{dx}\left( g(x) \right)}{(g(x))^{2}}$$ 9{-1}\влево(х\вправо)\вправо)}$$

Как вы понимаете, существует множество уравнений для производных, так что давайте уточним!

Производная функции

Нахождение производных функций обычно является отправной точкой вашего приключения с дифференциацией, поэтому обязательно освойте эти процедуры, прежде чем переходить к ограничениям и более сложным задачам дифференциации.

Как и во всем в жизни, во время работы полезно помнить о своих целях! Итак, какова наша цель с производными функций?

Когда мы берем производную функции, это потому, что мы хотим найти:

• Скорость изменения функции
• Наклон касательной в определенной точке функции

Вскоре мы рассмотрим, как это сделать; но сначала давайте расшифруем кое-что еще, что вы можете услышать при изучении производных функций.

Производная по x

Возможно, вы слышали, как учитель математики говорил о производной «по» переменной (вначале это обычно $$x$$), и вы не совсем уверены, что это действительно означает.

Если мы работаем с функцией — $$f(x)$$ — и хотим найти «производную по $$x$$», это просто означает, что мы ищем скорость при который $$f$$ изменяется при изменении $$x$$. По сути, это означает, что мы действительно фокусируемся на переменной $$x$$ и на том, как она влияет на нашу функцию.

Процесс нахождения производной функции

Если вы помните ключевые слова, вы помните, что процесс нахождения производной называется «дифференцированием».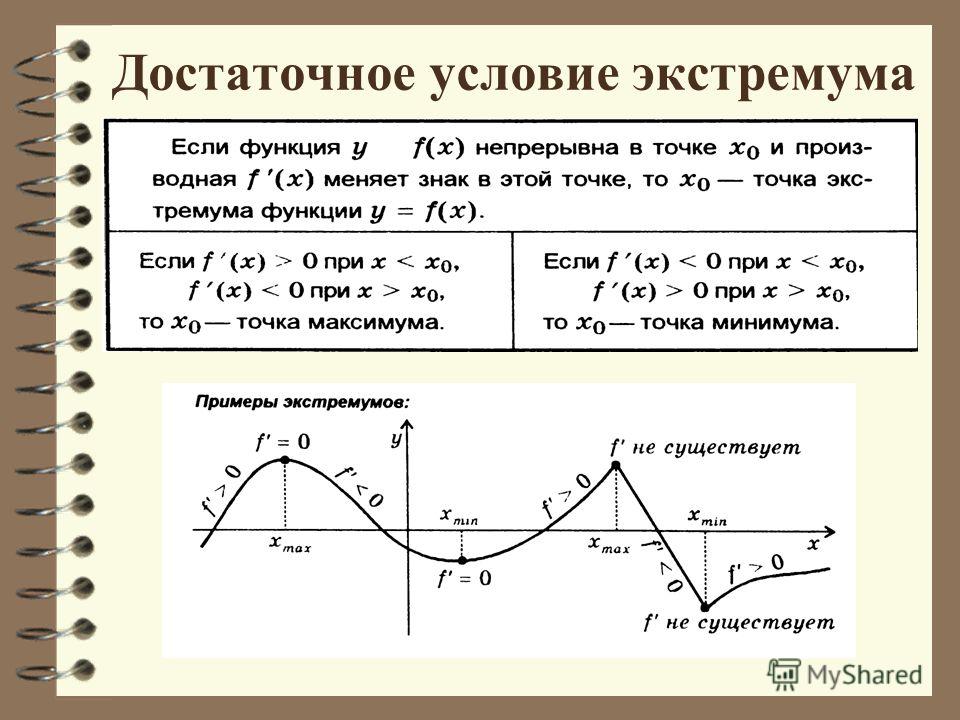 (Мы можем помочь, если вам нужно освежить словарный запас!)

Забавный факт: производная функции — это тоже функция, а ее значения — соответствующие производные в точке. По существу, если мы определяем производную функции $$f$$ при любом значении $$x$$, то наша производная $$f'(x)$$ представляет собой функцию, которая выводит значение $$f'(x )$$ для любого входа $$x$$ (по крайней мере, для которого эта производная существует).

Фактические шаги дифференциации будут варьироваться в зависимости от конкретной проблемы и сложности — мы можем подробно объяснить в приложении! — но вот обзор:

1. Возьмите производную от обеих частей уравнения
2. Использовать правила дифференцирования (также называемые «формулами производных»)
3. Найдите производную
4. Упростите выражение, если необходимо

Нужно больше? Перейдите, чтобы глубже погрузиться в производные функций.

Не забывайте: Вы также можете найти производные от выражений и интегралов, которые будут выглядеть немного иначе.

Что такое f’(x)?

$$f’(x)$$ обозначает производную. Итак, когда вы начнете брать производную функции $$f(x)$$, ваше решение — производная — будет помечено как $$f’(x)$$. Вы также можете увидеть $$f’(x)$$ в виде $$\frac{dy}{dx}$$ в определенных сценариях.

Будьте осторожны при чтении, потому что легко пропустить этот маленький апостроф. Когда мы видим $$f’(x)$$, мы видим производную, но $$f(x)$$ говорит нам, что это функция!

Производная и предельная: в чем разница?

Производные и лимиты не являются взаимозаменяемыми терминами, но есть некоторое совпадение.

Разница зависит от того, говорите ли вы о производных и пределах определенного значения функции или о функции в целом. Поясним:

• Производная функции в точке — это особый тип предела в этой точке — другими словами, каждая производная — это предел!
  • Численно значение производной в определенной точке функции говорит нам о мгновенной скорости изменения функции в этой точке.
  • Геометрически значение производной в определенной точке функции представляет собой наклон линии, проходящей касательной к графику функции в этой точке.
• Предел функции в точке представляет поведение функции вокруг этой точки. По сути, если поведение предсказуемо, то предел существует. 92дт$$

Вот как мы решаем первую практическую задачу в приложении:

00:00 / 00:00

Застряли на других производных практических задачах? Отсканируйте проблему с помощью приложения Photomath, чтобы мы могли помочь вам с каждым шагом!

Часто задаваемые вопросы
Каковы два определения производной?

Производная описывается либо как скорость изменения функции, либо как наклон касательной в определенной точке функции.

Что такое производная простыми словами?

Производная говорит нам о скорости изменения определенной переменной.

Как деривативы используются в реальной жизни?

Производные можно использовать для прогнозирования таких изменений, как колебания температуры при изменении климата, диапазоны магнитуд землетрясений, прогнозы переписи населения, изменения импульса и многое другое.

Есть домашнее задание по математике?

Зайдите в приложение Photomath, чтобы быстро найти пошаговые решения всех ваших математических задач.

Видео с вопросами: Нахождение производной рациональной функции с использованием предельного определения производных

Стенограмма видео

Используя определение производной, оцените 𝑑 на 𝑑𝑥 единицы на 𝑥 плюс один.

По определению, производная от 𝑓 от 𝑥 — 𝑑 по 𝑑𝑥 от 𝑓 от 𝑥 — это предел 𝑓 от 𝑥 плюс ℎ минус 𝑓 от 𝑥 по ℎ, когда ℎ приближается к нулю. Это также пишется как 𝑓 тире от 𝑥 или 𝑓 штрих от 𝑥, чтобы подчеркнуть, что это функция от 𝑥. Применим это определение к нашей задаче.

Знаменатель ℎ копируем из определения. Также, надеюсь, ясно, что 𝑓 из 𝑥 должно быть на один больше 𝑥 плюс один для нашего вопроса. Конечно, это в левой части уравнения. Возможно, немного сложнее понять, что такое 𝑓 из 𝑥 плюс ℎ. Ну, если 𝑓 из 𝑥 на один больше 𝑥 плюс один, то 𝑓 из 𝑥 плюс ℎ будет один больше 𝑥 плюс ℎ плюс один.

Теперь мы готовы найти этот предел. Важно отметить, что это предел, поскольку ℎ приближается к нулю. Это не предел, так как 𝑥 приближается к некоторому значению. И наш окончательный ответ будет в терминах 𝑥. Если мы попытаемся прямо заменить здесь ℎ равным нулю, мы получим неопределенную форму ноль над нулем. Если не верите мне, можете проверить.

Нам нужно упростить дробь в пределе и, надеюсь, найти множитель ℎ в числителе, чтобы сократить его на ℎ в знаменателе, прежде чем мы сможем вычислить предел. В настоящее время у нас есть дроби в нашей фракции. В числителе две дроби. Если мы умножим и числитель, и знаменатель на 𝑥 плюс ℎ плюс один, мы избавимся от одной из этих дробей.

Здесь мы распределили 𝑥 плюс ℎ плюс один по двум слагаемым в числителе. Итак, мы можем распознать первую дробь как единицу. Чтобы избавиться от другой дроби в числителе, мы умножаем на 𝑥 плюс один на 𝑥 плюс один. И снова упрощаем. Так что теперь наши знаменатели становятся намного сложнее, но наш числитель намного проще. А на самом деле его можно еще упростить.

Для начала можно избавиться от ненужных скобок вокруг 𝑥 плюс ℎ. И мы замечаем, что два 𝑥 сокращаются. У нас есть 𝑥, из которого мы затем вычитаем 𝑥. И что-то подобное происходит с теми. Так что у нас просто остался минус ℎ в числителе. И в знаменателе тоже есть множитель ℎ. Отменив эти множители, числитель станет отрицательным, а знаменатель будет равен 𝑥 плюс ℎ плюс один, умноженный на 𝑥 плюс один.

И, сократив этот множитель ℎ в числителе и знаменателе, мы теперь можем напрямую подставить. Подставив ноль вместо ℎ, мы получим минус один на 𝑥 плюс ноль плюс один, умноженный на 𝑥 плюс один. И, конечно же, нам не нужно писать это плюс ноль явно. Мы получаем минус один на 𝑥 плюс один, умноженный на 𝑥 плюс один, следовательно, или минус один на 𝑥 плюс один в квадрате.

No related posts.