Найдите длину вектора 10 24: Найдите длину вектора а (-10,24)

2.6. ВЕКТОРЫ НА ПЛОСКОСТИ — ГИА-ЕГЭ 2021

2463. Вектор AB с началом в точке А(3, 2) имеет координа­ты (—6, 6). Найдите абсциссу точки В.

2464. Вектор AB с началом в точке А(9, 2) имеет координа­ты (6, 2). Найдите ординату точки В.

2465. Вектор AB с началом в точке А(—12, -3) имеет коор­динаты (8, 4). Найдите абсциссу точки В.

2466. Вектор AB с началом в точке А(3, 2) имеет координа­ты (6, -6). Найдите ординату точки В.

2467. Вектор ABС началом в точке А(9, 2) имеет координа­ты (2, 6). Найдите абсциссу точки В.

2468. Вектор ABС началом в точке A(12, -1) имеет коорди­наты (8, -3). Найдите сумму координат точки В.

2469. Вектор ABС началом в точке А(2,-3) имеет коорди­наты (4, 18). Найдите сумму координат точки В.

2470. Вектор AB с началом в точке A(9, 1) имеет координа­ты (5, 3).

Найдите сумму координат точки В.

2471. Вектор AB с началом в точке А(4,-2) имеет коорди­наты (6, -7). Найдите сумму координат точки В.

2472. Вектор AB с началом в точке A(-15, 2) имеет коорди­наты (6, -3). Найдите сумму координат точки В.

2473. Вектор AB с концом в точке B(9, 1) имеет координа­ты (5, 3). Найдите ординату точки А.

2474. Вектор AB с концом в точке B(8, 1) имеет координа­ты (5, 4). Найдите абсциссу точки А.

2475. Вектор AB с концом в точке В(8, 2) имеет координа­ты (6, -11). Найдите ординату точки А.

2476. Вектор AB с концом в точке B(-21, 4) Имеет коорди­наты (8, 9). Найдите абсциссу точки А.

2477. Вектор AB с концом в точке B(10, -1) имеет коорди­наты (8, -7). Найдите ординату точки

А.

2478. Вектор AB с концом в точке. B(10, -1) имеет коорди­наты (8, -7). Найдите сумму координат точки А.

2479. Вектор AB с концом в точке В(8, -3) имеет координа­ты (4, -11). Найдите сумму координат точки А.

2480. Вектор ABС концом в точке B(-22, -1) имеет коор­динаты (8, 7). Найдите сумму координат точки А.

2481. Вектор ABС концом в точке В(-7, 2) имеет координа­ты (6, -10). Найдите сумму координат точки А.

2482. Вектор ABС концом в точке B(5, 1) имеет координа­ты (5, 7). Найдите сумму координат точки А.

2483. Найдите длину вектора а (-12, -9).

2484. Найдите длину вектора а (12, -5).

2485. Найдите длину вектора а (-8, -15).

2486. Найдите длину вектора А(3, 4).

2487. Найдите длину вектора а (15, -8).

2488. Две стороны прямоугольника ABCDРавны 28 и 21.

Найдите длину вектора AC.

2489. Две стороны прямоугольника ABCDРавны 42 и 40.

Найдите длину вектора AC.

2490. Две стороны прямоугольника ABCDРавны 60 и 25.

Найдите длину вектора AC.

2491. Две стороны прямоугольника ABCDРавны 15 и 36. Найдите длину вектора AC.

2492. Две стороны прямоугольника ABCDРавны 4 и 3. Най­дите длину вектора AC.

2493. Две стороны прямоугольника ABCDРавны 32 и 24. Найдите длину суммы векторов ABИ AD .

2494. Две стороны прямоугольника ABCDРавны 48 и 20. Найдите длину суммы векторов

ABИ AD .

2495. Две стороны прямоугольника ABCDРавны 63 И 60.

Найдите длину суммы векторов ABИ AD .

2496. Две стороны прямоугольника ABCDРавны 36 и 27. Найдите длину суммы векторов ABИ AD .

2497. Две стороны прямоугольника ABCDРавны 3 и 4. Най­дите длину суммы векторов ABИ AD .

2498. Две стороны прямоугольника ABCDРавны 16 и 30. Найдите длину разности векторов ABИ AD .

2499. Две стороны прямоугольника ABCDРавны 5 и 12. Найдите длину разности векторов ABИ AD .

2500. Две стороны прямоугольника ABCDРавны 45 и 24. Найдите длину разности векторов ABИ AD .

2501.

Две стороны прямоугольника ABC-D равны 24 и 45. Найдите длину разности векторов AB и AD.

2502. Две стороны прямоугольника ABCDРавны 8 и 15. Найдите длину разности векторов AB и AD.

2503. Две стороны прямоугольника ABCDРавны 4 и 21. Найдите скалярное произведение векторов AB и AD.

2504. Две стороны прямоугольника ABCDРавны 4 и 18. Найдите скалярное произведение векторов AB и AD.

2505. Две стороны прямоугольника ABCD равны 15 и 30. Найдите скалярное произведение векторов AB и AD.

2506. Две стороны прямоугольника ABCDРавны 4 и 22. Найдите скалярное произведение векторов AB и AD .

2507. Две стороны прямоугольника ABCD равны 40 и 75. Найдите скалярное произведение векторов AB и AD.

2508. В прямоугольнике ABCDИзвестны стороны AB = 8 и AD = 68. Диагонали пересекаются в точке

О. Найдите длину суммы векторов АО и ВО.

2509. В Прямоугольнике ABCDИзвестны стороны AB = 17 и AD = 34. Диагонали пересекаются в точке О. Найдите длину суммы векторов АО и ВО.

2510. В прямоугольнике ABCDИзвестны стороны AB = 25 и AD = 46. Диагонали пересекаются в точке О. Найдите длину суммы векторов АО и ВО.

2511. В прямоугольнике ABCDИзвестны стороны AB = 21 и AD = 40. Диагонали пересекаются в точке О. Найдите длину суммы векторов АО и ВО.

2512. В прямоугольнике ABCDИзвестны стороны AB = 13 и AD = 53.Диагонали пересекаются в точке О. Найдите длину суммы векторов АО и ВО.

2513.

В прямоугольнике ABCDИзвестны стороны AB = 33 и AD = 58. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.

2514. В прямоугольнике ABCDИзвестны стороны AB = 4 и AD = 61. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.

2515. В прямоугольнике ABCDИзвестны стороны AB = 10 и AD = 62. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.

2516. В прямоугольнике ABCDИзвестны стороны AB = 5 и AD = 77. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.

2517. В прямоугольнике ABCDИзвестны стороны AB = 7 и AD =71. Диагонали пересекаются в точке

О. Найдите длину разности векторов АО и ВО.

2518. В ромбе ABCDИзвестны диагонали AC =33 и BD = 58. Найдите длину вектора AB + AD .

2519. В ромбе ABCDИзвестны диагонали AC = 20 и BD = 35. Найдите длину вектора AB + AD .

2520. В ромбе ABCDИзвестны диагонали AC =14 и BD = 76. Найдите длину вектора AB + AD .

2521. В ромбе ABCDИзвестны диагонали AC = 8 и BD = 67. Найдите длину вектора AB + AD .

2522. В ромбе ABCDИзвестны диагонали AC =15 и BD = 31. Найдите длину вектора AB + AD .

2523. В Ромбе ABCDИзвестны диагонали

AC = 8 И BD = 67. Найдите длину вектора AB — AD .

2524. В Ромбе ABCD известны диагонали AC =14 и

BD = 76. Найдите* длину вектора AB — AD .

2525. В ромбе ABCD известны диагонали AC = 33 и

BD —58. Найдите длину вектора AB — AD .

2526. В ромбе ABCD известны диагонали AC =10 и

BD = 70. Найдите длину вектора AB — AD .

2527. В ромбе ABCD известны диагонали AC = 22 и

BD = 88. Найдите длину вектора AB — AD .

2528. Диагонали ромба ABCDРавны 24 и 45. Найдите длину вектора AB — AC.

2529. Диагонали ромба ABCDРавны 9 И 12. Найдите длину вектора AB — AC .

2530. Диагонали ромба ABCDРавны 28 и 45. Найдите длину вектора AB — AC .

2531. Диагонали ромба ABCDРавны 16 и 30. Найдите длину вектора AB — AC .

2532. Диагонали ромба ABCDРавны 20 и 48. Найдите длину вектора AB — AC.

2533. Диагонали ромба ABCDПересекаются в точке О и рав­ны 3 и 4. Найдите длину вектора АО + ВО.

2534. Диагонали ромба ABCDПересекаются в точке О и рав­ны 24 и 10. Найдите длину вектора АО + ВО.

2535. Диагонали ромба ABCDПересекаются в точке О и рав­ны 7 и 24. Найдите длину вектора АО + ВО.

2536. Диагонали ромба ABCDПересекаются в точке О и рав­ны 25 и 60. Найдите длину вектора АО + ВО.

2537.

Диагонали ромба ABCDПересекаются в точке О и рав­ны 9 и 40. Найдите длину вектора АО + ВО.

2538. Диагонали ромба ABCDПересекаются в точке О и рав­ны 36 и 27. Найдите длину вектора АО ВО.

2539. Диагонали ромба ABCDПересекаются в точке О и рав­ны 63 И 60. Найдите длину вектора АО — ВО.

2540. Диагонали ромба ABCDПересекаются в точке О и рав­ны 21 и 72. Найдите длину вектора АО — ВО.

2541. Диагонали ромба ABCD пересекаются в точке О и рав­ны 36 и 15. Найдите длину вектора АО — ВО.

2542. Диагонали ромба ABCDПересекаются в точке О и рав­ны 14 и 48. Найдите длину вектора AO—BO .

2543. Диагонали ромба ABCDПересекаются в точке О и рав­ны 4 и 19. Найдите скалярное произведение векторов АО и ВО.

2544. Диагонали ромба ABCDПересекаются в точке О и рав­ны 24 и 10. Найдите скалярное произведение векторов АО и ВО.

2545. Диагонали ромба ABCDПересекаются в точке О и рав­ны 32 и 60. Найдите скалярное произведение векторов АО и ВО.

2546. Диагонали ромба ABCDПересекаются в точке О и рав­ны 144 и 60. Найдите скалярное произведение векто­ров АО и ВО.

2547. Диагонали ромба ABCDПересекаются в точке О и рав­ны 48 и 54. Найдите скалярное произведение векторов АО и ВО.

2548. Стороны правильного треугольника ABC равны 47∖∕3. Найдите длину вектора AB + AC .

2549. Стороны правильного треугольника ABCРавны 25-J3 . Найдите длину вектора AB + AC .

2550. Стороны правильного треугольника ABCРавны 40∖∕3 . Найдите длину вектора AB + AC .

2551. Стороны правильного треугольника ABC равны 29\/3. Найдите длину вектора AB + AC.

2552. Стороны правильного треугольника ABC равны 12∖∕3. Найдите длину вектора AB + AC.

2553. Стороны правильного треугольника ABC равны 42. Найдите длину вектора АД — AC.

2554. Стороны правильного треугольника ABC равны 28. Найдите длину вектора AB — AC.

2555. Стороны правильного треугольника ABC равны 14. Найдите длину вектора AB — AC.

2556. Стороны правильного треугольника ABCРавны 39. Найдите длину вектора AB — AC.

2557. Стороны правильного треугольника ABC равны 9. Найдите длину вектора AB — AC.

2558. Стороны правильного треугольника ABC равны 40. Найдите скалярное произведение векторов AB и AC.

2559. Стороны правильного треугольника ABC равны 1. Найдите скалярное произведение векторов AB и AC.

2560. Стороны правильного треугольника ABC равны 23.

Найдите скалярное произведение векторов AB и AC.

2561. Стороны правильного треугольника ABC равны 42. Найдите скалярное произведение векторов AB и AC.

2562. Стороны правильного треугольника ABC равны 33. Найдите скалярное произведение векторов AB и AC.

Векторы 9 класс онлайн-подготовка на Ростелеком Лицей

Определение вектора

 

Жизнь бесконечна, но для того, чтобы решать конкретные практические задачи, мы пытаемся приблизить реальность моделью с интересующей нас степенью точности. Описывать человека можно очень долго, но если нужно сшить костюм, то описание сузится до набора чисел – рост, длина рукавов, обхват груди и т. д. Похожая ситуация и с погодой – про нее можно рассказывать с любой степенью подробности. Но в прогнозе погоды обычно ограничиваются несколькими важными параметрами: температура воздуха, скорость ветра, атмосферное давление и т. д.

 

В рассмотренных примерах для описания объектов выбранной модели мы должны измерить характеристики этих объектов (например, рост человека или температуру воздуха). В некоторых случаях достаточно измерить одну величину. Так, покупая на рынке яблоки, мы их только взвешиваем. Нас не интересует диаметр яблок или их температура.

Но в примерах с костюмом или погодой измерением одной величины не обойтись. Т. е. один объект может описываться набором значений нескольких характеристик (двух, трех и т. д.). Такая ситуация нам уже встречалась и в математике: треугольник мы однозначно определяли длинами трех сторон или длинами двух сторон и угла между ними.

Ваш друг рассказал, что выехал из Москвы и проехал 170 км. Где он может находиться? Понятно, что его путь составил 170 км. Но куда он переместился? Он мог оказаться около Твери, Калуги, Тулы, Рязани, Владимира и т. д. Если бы речь шла об идеальной ситуации – движении в чистом поле, то он мог бы оказаться в любой точке окружности с центром в Москве и радиусом 170 км (см. рис. 1). Конкретное местоположение зависит от выбранного направления.

Рис. 1. Окружность с центром в Москве и радиусом 170 км

Перемещение на юг приведет нас в Тулу, а на северо-запад – в Тверь. Соединим Москву с Тулой отрезком и отметим стрелкой направление (см. рис. 2). Такой направленный отрезок называется перемещением (вспомните уроки физики: это направленный отрезок, соединяющий начало и конец движения).

Рис. 2. Перемещение Москва – Тула

Теперь Москву с Тверью тоже соединим направленным отрезком (см. рис. 3). Это другое перемещение. Длины этих перемещений равны. Но направления у них были разные. Поэтому сами перемещения тоже являются разными.

Рис. 3. Перемещения Москва – Тула и Москва – Тверь одинаковы по длине, но имеют разные направления

Понятно, что если одинаковыми будут только направления, но длины перемещений окажутся разными, то и сами перемещения тоже окажутся разными. Посмотрите на перемещения Москва – Владимир и Москва – Нижний Новгород. У них практически одинаковые направления, но у второго в два раза больше длина.

Рис. 4. Перемещения Москва – Владимир и Москва – Нижний Новгород имеют практически одинаковые направления, но разные длины

Рассмотрим два последовательных перемещения: Москва – Владимир и Владимир – Рязань. Откуда и куда мы в итоге переместились? Из Москвы в Рязань. Два последовательных перемещения дают нам новое (см. рис. 5). И, как видим, длина итогового перемещения здесь не равна сумме длин исходных.

Рис. 5. Два последовательных перемещения Москва – Владимир и Владимир – Рязань дают новое – Москва – Рязань

Т. е. для итогового перемещения не важна траектория, по которой мы двигались. Важны начальная и конечная точки. Например, последовательные перемещения Москва – Владимир – Калуга – Рязань – Тула эквивалентны простому перемещению Москва – Тула (см. рис. 6).

Рис. 6. Перемещение Москва – Владимир – Калуга – Рязань – Тула эквивалентно перемещению Москва – Тула

Рассмотрим еще один пример. Два человека несут сумку. Каждый из них прикладывает определенную силу к ручкам сумки. Результат их взаимодействия будет зависеть как от величины сил, так и от их направления (см. рис. 7).

Рис. 7. Результат взаимодействия людей, которые несут сумку, зависит и от величины сил, и от их направления

Силу, как и перемещение, удобно изображать направленным отрезком: чем длиннее отрезок, тем больше численное значение силы; направление действия силы совпадает с направлением отрезка.

И таких величин, которые можно описать, используя числовое значение и направление, достаточно много. Кроме перемещения и силы, таким образом можно описывать, например, скорость  и ускорение тела .

Ну а раз есть целый класс подобных объектов, то для их описания был придуман удобный инструмент, который назвали вектором. Величины, которые описываются с помощью векторов, как вы уже слышали на уроках физики, называются векторными величинами.

Сформулируем строгое определение: вектор – это направленный отрезок, т. е. отрезок, для которого указаны начало и конец (задано направление).

Изображается в виде отрезка со стрелкой на конце. Обозначается либо большими буквами со стрелкой наверху: , либо одной маленькой тоже со стрелкой наверху:  (см. рис. 8).

Рис. 8. Обозначения вектора

Часто вектор изображают без буквенных обозначений (см. рис. 9):

Рис. 9. Вектор без буквенных обозначений

Мы ввели вектор как инструмент для описания перемещения, силы, скорости и т. д. Но для решения различных задач нужно отработать технику работы с векторами. Мы уже сталкивались с такой ситуацией – ввели натуральные числа как удобный инструмент описания количества, а затем начали изучать технику работы с числами – сложение, умножение и т. д.

 

Равные векторы

 

 

Что можно делать с векторами? Мы уже рассмотрели несколько примеров задач, в которых необходимо сложить перемещения или силы, следовательно, нужно научиться складывать векторы. В дальнейшем мы поговорим и о других операциях, которые можно делать с векторами, а также о различных свойствах векторов, т. е. мы переходим непосредственно к технике работы с векторами.

 

Итак, пусть дан вектор  (см. рис. 10):

Рис. 10. Вектор

Длину отрезка  назовем модулем вектора или просто длиной вектора. Обозначение такое же, как для модуля числа . Модуль вектора соответствует численному значению физической величины: длине перемещения (расстоянию между начальной и конечной точками), величине силы и т. д.

Модуль вектора можно найти так же, как и длину отрезка, если задан масштаб (см. рис. 11). Например, ,  (выбираем в качестве единицы измерения длины  клетку). Модуль вектора  можем найти, используя теорему Пифагора, как гипотенузу соответствующего прямоугольного треугольника: .

Рис. 11. Длину вектора можно найти, если задан масштаб

Как сравнивать длины векторов понятно – в этом смысле задача сравнения сводится к задаче сравнения длин соответствующих отрезков, которую мы уже умеем решать. А как сравнивать (и можно ли вообще это делать) направления разных векторов?

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых (см. рис. 12). Векторы , ,  коллинеарны друг другу. Вектор  не коллинеарен ни одному другому. Если совсем просто, то коллинеарность – это параллельность векторов.

Рис. 12. Коллинеарные векторы , ,

Коллинеарные векторы могут быть сонаправлены, как  и , или противоположно направлены, как  и  или  и .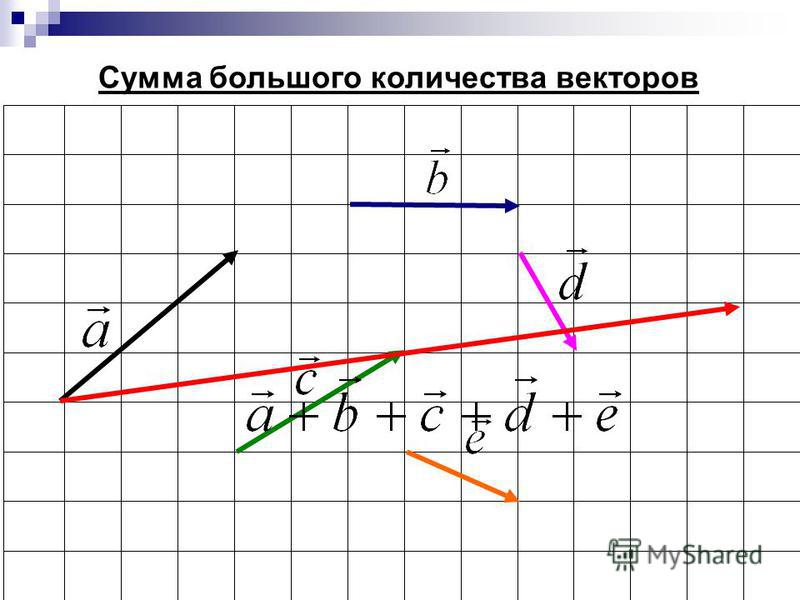 Обозначаются двумя стрелками в одну или разные стороны соответственно: , , .

Поскольку векторы определяются двумя характеристиками – модулем и направлением, то они будут равны, если у них совпадают оба эти параметра. Т. е. равными будут векторы, у которых равны длины и которые являются сонаправленными.

Прежде чем формулировать строгое определение, посмотрим, согласуется ли это определение с логикой и жизненным опытом. Рассмотрим в качестве примера перемещение.

Нарисуем на листе бумаги два одинаковых вектора (см. рис. 13):

Рис. 13. Одинаковые векторы  и

Накроем лист бумаги стеклом и посадим муху над точкой . Пусть муха переползет в точку  (см. рис. 14). Вектор перемещения .

Рис. 14. Вектор перемещения

Вернем муху назад и сдвинем под стеклом лист так, чтобы муха оказалась над точкой , а затем повторила свой предыдущий путь. В результате она окажется в точке  (см. рис. 15). Вектор перемещения .

Рис. 15. Вектор перемещения

Но ведь муха совершала одно и то же перемещение по стеклу. Она могла даже не видеть листа бумаги под стеклом. Конечно, разумно считать два рассмотренных перемещения одинаковыми, равными.

Векторы называются равными, если они сонаправлены и их длины равны (равенство векторов записывается как ):

Обратите внимание, что отдельно равенство модулей векторов или их сонаправленность не дают нам оснований говорить о равенстве векторов.

Действительно, в примере с другом, который отъехал от Москвы на 170 км, мы говорили о разных векторах одинаковой длины. Понятно, что перемещения, которые из одной и той же точки приводят нас в совершенно разные места, нельзя считать одинаковыми.

Аналогично в ситуации с сонаправленными векторами – можно выехать в одном направлении, но проехать 10 км, а можно – 100 км. Понятно, что перемещения, а значит, и векторы в этих случаях будут разными.

 

Правило треугольника

 

 

Мы определили равные векторы, т. е. ввели классы эквивалентности. Теперь можно поговорить об операциях, которые можно выполнять с векторами. Мы уже говорили, что несколько последовательных перемещений – это сложение перемещений, одновременное приложение к одному телу нескольких сил – это сложение сил. Если вы идете по движущемуся эскалатору, то ваша скорость относительно Земли – это сложение вашей скорости относительно эскалатора и скорости эскалатора относительно Земли.

 

Понятно, что для решения задач необходимо ввести операцию сложения для векторов. Перемещение естественным образом подсказывает нам, как складывать векторы.

Пусть мы переместились из точки  в точку . Вектор перемещения . Далее мы переместились из точки  в точку . Вектор перемещения . Итоговое перемещение  складывается из двух первых перемещений (см. рис. 16). Тогда: .

Рис. 16. Перемещение  складывается из перемещений  и

Такое правило сложения двух векторов называют правилом треугольника. Оно непосредственно следует из того, что два последовательных перемещения эквивалентны перемещению из начальной точки в конечную.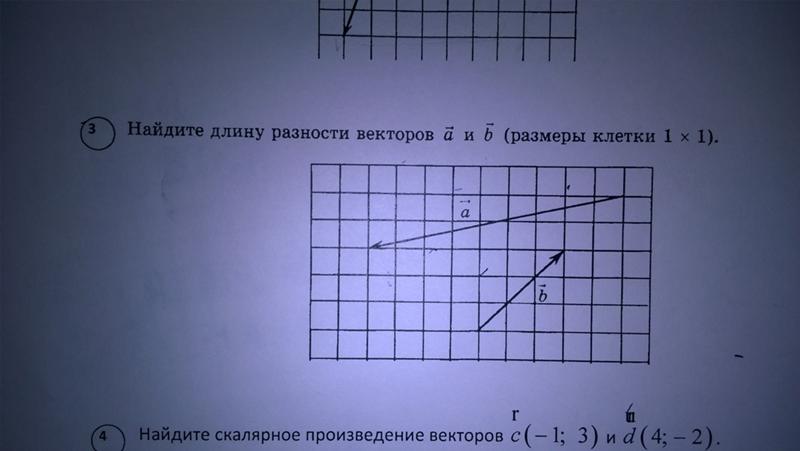

Обратите внимание, что если точка  не принадлежит отрезку , то сумма длин векторов всегда больше длине вектора суммы (неравенство треугольника). И только если точка  принадлежит отрезку , то сумма длин векторов равна длине суммы. Можно сформулировать это так:

Можем ли мы применять правило треугольника для сложения двух произвольных векторов? Конечно. Рассмотрим векторы  и  (см. рис. 17):

Рис. 17. Рассматриваемые векторы  и

Построим четырехугольник  так, чтобы вектор  был равен вектору  (см. рис. 18). Полученный четырехугольник является параллелограммом, т. к. , .

Рис. 18. Параллелограмм

Т. к. векторы  равны, то  (по правилу треугольника) (см. рис. 19).

Рис. 19. Сумма векторов  и  равна вектору

Операцию, которую мы выполнили с вектором , чтобы получить равный ему вектор , называют параллельным переносом (см. рис. 20). Подробнее о ней мы поговорим чуть позже.

Рис. 20. Параллельный перенос

Частным, более простым случаем является сложение коллинеарных векторов. Если векторы сонаправлены, то, совместив параллельным переносом конец одного и начало другого, мы получим новый вектор, направленный в ту же сторону, что и слагаемые, и длина которого равна сумме длин слагаемых (см. рис. 21).

Рис. 21. Сложение сонаправленных коллинеарных векторов

Если векторы разнонаправленны, то после совмещения конца одного и начала другого мы получим короткий вектор суммы, который направлен в ту сторону, куда был направлен более длинный вектор, и длина суммы будет равна разности длин исходных векторов (см. рис. 22). Эта ситуация очень напоминает сумму двух чисел одного знака в первом случае и сумму двух чисел с разными знаками во втором случае.

Рис. 22. Сложение разнонаправленных коллинеарных векторов

 

Правило параллелограмма

 

 

Пример со сложением сил будет отличаться от сложений перемещений. Все дело в том, что перемещения могут быть последовательными. А о сумме сил мы говорим в тех случаях, когда две силы приложены к одному телу одновременно.

 

Если на горизонтальной поверхности человек тянет сани, то они движутся в ту же самую сторону, куда направлен вектор силы тяги. Если два человека тянут сани чуть в разных направлениях, то сани движутся по направлению между этими двумя этими векторами (см. рис. 23). Мы это интуитивно хорошо понимаем, когда выполняем вдвоем подобного рода работу (ранее рассматривали пример с сумкой, которую несут двое).

Рис. 23. Если два человека тянут сани в разных направлениях, то сани движутся по направлению между этими двумя этими векторами

Задача сложения сил сводится к задаче сложения векторов, которые имеют общее начало. Рассмотрим сумму векторов . Построим вектор , равный вектору  (см. рис. 24).

Рис. 24. Векторы  и  имеют общее начало, векторы

Мы уже знаем, что по правилу треугольника:

Но что такое вектор ? Рассмотрим четырехугольник  (см. рис. 25).

Рис. 25. Рассматриваемый четырехугольник

В нем ,  (в силу равенства векторов ). Значит, по признаку параллелограмма,  – параллелограмм.

Т. е. суммой векторов с общим началом будет вектор диагонали параллелограмма, построенного на этих двух векторах, имеющий то же начало (см. рис. 26). Это правило называется правилом параллелограмма.

Рис. 26. Правило параллелограмма

Так как же складывать два вектора, по правилу треугольника или параллелограмма? Мы получили правило параллелограмма через правило треугольника. Т. е. оба правила верны. Какое из правил применять, зависит от ситуации – если нам нужно сложить векторы, у которых конец одного совпадает с началом другого, то удобнее пользоваться правилом треугольника. Если же мы складываем векторы с одинаковым началом, то – правилом параллелограмма. В остальных случаях можно выбрать любое из двух правил, которое покажется более удобным.

 

Вычитание векторов

 

 

Для чисел после операции сложения мы естественным образом ввели обратную операцию – вычитание. По аналогии поступим и с векторами.

 

Т. к. , то естественно считать, что . Теперь можно сформулировать алгоритм вычитания векторов.

Пусть нужно из вектора  вычесть вектор . Совместим их начала. Соединим концы векторов и направим к уменьшаемому, т. е. к вектору . Полученный вектор и есть разность двух векторов (см. рис. 27).

Рис. 27. Разность векторов  и

Изобразим операцию сложения и вычитания векторов на одной картинке. Пусть два вектора  и  имеют общее начало. Достроим рисунок до параллелограмма.

Тогда одна диагональ является суммой векторов , а вторая – разностью (см. рис. 28).

Рис. 28. Сумма и разность векторов  и

Иногда при решении задач забывают, в какую сторону направить вектор разности. Здесь есть очень простой совет: проверьте себя сложением. Если , значит, все в порядке.

 

Умножение вектора на число

 

 

Мы поговорили о сложении и вычитании векторов. Если продолжать аналогию с числами, то следующий шаг – введение операции умножения. Вспомним, что умножение – это краткая запись сложения одинаковых элементов: .

 

Если тело совершило  раза одно и то же перемещение, равное , то можно сказать, что оно переместилось в том же направлении на расстояние, равное .

Другой пример: если говорят, что машина увеличила скорость в  раза, то обычно это означает, что направление не изменилось, а увеличилось численное значение скорости в  раза. Описанные операции называются умножением вектора на число.

Сложим вектор  с самим собой  раза:  – получаем вектор, длина которого в  раза больше, а направление совпадает с . Новый вектор мы так и обозначили: . Это хорошо согласуется с понятием умножения как многократного сложения одинаковых элементов. В самом деле, если вектор  сложить с самим собой  раза, то как раз получится такой вектор  (см. рис. 29).

Рис. 29. Сложение вектора  с самим собой  раза

Если умножить вектор  на , то его длина увеличится в  раза, а направление снова останется прежним (см. рис. 30).

Рис. 30. Умножение вектора  на

Умножение вектора  на число ноль дает нам вектор нулевой длины. Назовем его нулевым вектором:

Нулевой вектор – это вектор нулевой длины. Начало и конец этого вектора совпадают. Направление у него не определено.

Давайте теперь подумаем, что может означать умножение на отрицательное число.

Возьмем для примера умножение на . Вспомним умножение чисел. Если умножить любое число на , получим противоположное ему число: , т. е. число, которое в сумме с данным дает ноль: .

Используем это определение и для векторов: для вектора  назовем противоположным такой вектор , чтобы они в сумме давали ноль-вектор:

Вернемся к примеру с перемещением. Ноль-вектор – это перемещение, начало и конец которого – одна и та же точка . Пусть мы переместились из точки  в точку . Каким должно быть перемещение, чтобы в итоге мы снова оказались в точке ? Понятно, что это перемещение из точки  в точку . Получаем, что: . Нетрудно увидеть, что это у противоположного вектора должна быть такая же длина, но противоположное направление.

Тогда, по аналогии с числами, умножение вектора  на число  дает противоположный вектор:

Тогда при умножении вектора на произвольное отрицательное число будем получать вектор, противоположно направленный, длина которого – это длина первого вектора, умноженная на модуль этого числа (см. рис. 31).

Рис. 31. Умножение вектора  на

Например, при умножении вектора  на  получим противоположно направленный вектор в  раза длиннее, а при умножении на  тоже противоположно направленный, но в  раза короче:

Заметим, что векторы  и  всегда коллинеарны:

1. если , то сонаправлены;
2. если , то противоположно направлены

Оказывается, верно и обратное утверждение: если векторы  и  коллинеарны, то существует такое число , что:

Действительно, если векторы  и  сонаправлены, то в качестве , если противоположно направлены, то   (в силу определения умножения вектора на число).

Заключение

Мы рассмотрели умножение вектора на число. А можно ли умножать векторы между собой? Оказывается, можно, причем разными способами. Но подробнее об этом мы поговорим на следующих уроках.

 

Список литературы

1. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия. 9 класс. Учебник. – М.: «Просвещение», 2014.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия. 9 класс. Учебник. – М.: «Просвещение», 2018.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия. 9 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «onlinemschool.com» (Источник)
2. Интернет-портал «math34.ru» (Источник)
3. Интернет-портал «yaklass.ru» (Источник)

 

Домашнее задание

1. Стороны правильного треугольника  равны . Найти длину вектора .
2. Две стороны прямоугольника  равны  и . Найти длину суммы .
3. Найти длину вектора:

 

 

Самостоятельная работа по геометрии 9 класс Векторы (по материалам ОГЭ) с ответами | Учебно-методический материал по геометрии (9 класс) на тему:

Опубликовано 21.10.2015 — 19:38 — Чернышова Людмила Антоновна

Работа по текстам Закрытого банка заданий ОГЭ 2016

Скачать:

Предварительный просмотр:

Вариант 1

1. Две стороны прямоугольника ABCD равны 42 и 40. Найдите длину вектора   .

2. Две стороны прямоугольника ABCD равны 48 и 20. Найдите длину суммы векторов     и   .
3. Две стороны прямоугольника ABCD равны 5 и 12. Найдите длину разности векторов     и   .
4. В прямоугольнике ABCD  известны стороны АВ = 17 и AD = 34. Диагонали пересекаются в точке О. Найдите длину суммы векторов     и    .
5. В ромбе ABCD  диагонали АС = 20 и BD = 35. Найдите длину вектора     +  .
6. В ромбе ABCD  диагонали АС = 14 и BD = 76. Найдите длину вектора     —  .
7. Найдите среднюю линию трапеции, если её основания 33 и 27.
8. Средняя линия трапеции равна 25,5.а меньшее основание равно 21. Найдите большее основание трапеции.
9. Основания трапеции равны 3 и 17. Найдите больший из отрезков, на которые делит  среднюю линию одна из её диагоналей.
10. Катеты прямоугольного треугольника равны 18 и 24.  Найдите гипотенузу.

___________________________________________________________________

Вариант 2

1. Две стороны прямоугольника ABCD равны 60 и 25. Найдите длину вектора   .
2. Две стороны прямоугольника ABCD равны 63 и 60. Найдите длину суммы векторов     и   .
3. Две стороны прямоугольника ABCD равны 45 и 24. Найдите длину разности векторов     и   .
4. В прямоугольнике ABCD  известны стороны АВ = 25 и AD = 46. Диагонали пересекаются в точке О. Найдите длину суммы векторов    и   .
5. В ромбе ABCD  диагонали АС = 14 и BD = 76. Найдите длину вектора     +  .
6. В ромбе ABCD  диагонали АС = 33 и BD = 58. Найдите длину вектора     —  .
7. Найдите среднюю линию трапеции, если её основания 16 и 32.
8. Средняя линия трапеции равна 23.а меньшее основание равно 15. Найдите большее основание трапеции.
9. Основания трапеции равны 6 и 11. Найдите больший из отрезков, на которые делит  среднюю линию одна из её диагоналей.
10. Катеты прямоугольного треугольника равны 20 и 21.  Найдите гипотенузу.

Вариант 3

1. Две стороны прямоугольника ABCD равны 28 и 21. Найдите длину вектора   .
2. Две стороны прямоугольника ABCD равны 32 и 24. Найдите длину суммы векторов     и  .
3. Две стороны прямоугольника ABCD равны 16 и 30. Найдите длину разности векторов     и  .
4. В прямоугольнике ABCD  известны стороны АВ = 8 и AD = 68. Диагонали пересекаются в точке О. Найдите длину суммы векторов     и    .
5. В ромбе ABCD  диагонали АС = 33 и BD = 58. Найдите длину вектора     +  .
6. В ромбе ABCD  диагонали АС = 3 и BD = 67. Найдите длину вектора     —  .
7. Найдите среднюю линию трапеции, если её основания 46 и 66.
8. Средняя линия трапеции равна 11.а меньшее основание равно 5. Найдите большее основание трапеции.
9. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит  среднюю линию одна из её диагоналей.
10. Катеты прямоугольного треугольника равны 9 и 40.  Найдите гипотенузу.

Ответы:

	1	2	3	4	5	6	7	8	9	10
Вар. 1	58	52	13	34	20	76	30	30	8,5	30
Вар.2	65	87	51	46	14	58	24	31	5,5	29
Вар.3	35	40	34	68	33	67	56	17	5	41

По теме: методические разработки, презентации и конспекты

Самостоятельная работа по геометрии для 11 класса по теме: «Скалярное произведение векторов»

Самостоятельная работа составлена в 4 вариантах по 6 задач в каждом. Предназначена для проверки и отработки умений решать задачи на нахождение угла между векторами, скалярного произведения векторов по…

Самостоятельная работа по геометрии 9 класс.Векторы.

В данной работе рассматривается тема: построение векторов….

Самостоятельная работа по геометрии 9 класс по теме «Векторы»

Самостоятельная работа состоит из двух вариантов.. Одно задание на  среднюю линии трапеции, второе задание на построение векторов….

Самостоятельная работа по геометрии по теме «Векторы», 9 кл.

Тема «Векторы и операции над ними», самостоятельная работа…

Самостоятельная работа по геометрии 11 класс. Координаты точки и координаты вектора.

Самостоятельная работа по геометрии по теме: «Координаты точки и координаты вектора», 11 класс. УМК Л.С, Атанасян, В.Ф. Бутузов….

Самостоятельная работа по геометрии 9 класс «Понятие вектора»

Самостоятельная работа по геометрии 9 класс«Понятие вектора&raquo…

Самостоятельная работа по геометрии для 9 класса Векторы

Самостоятельная работа по геометрии для 9 класса Векторы. ..

Поделиться:

 

Найти единичный вектор в том же направлении, что и заданный вектор

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочие

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все ресурсы Precalculus

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

Precalculus Help » Матрицы и векторы » Алгебраические векторы и параметрические уравнения » Найдите единичный вектор в том же направлении, что и заданный вектор

Найдите единичный вектор, направленный в том же направлении, что и вектор Пояснение:

Чтобы найти единичный вектор в том же направлении, что и вектор, мы разделим его на его модуль.

Величина  равна .

Мы делим вектор на его модуль, чтобы получить единичный вектор:

или

Все единичные векторы имеют модуль, поэтому для проверки правильности:

Сообщить об ошибке

Единичный вектор имеет длину .

По заданному вектору

найдите единичный вектор в том же направлении.

Возможные ответы:

Правильный ответ:

Пояснение:

Во-первых, вы должны найти длину вектора. Это дается уравнением:

Затем, деление вектора на его длину дает единичный вектор в том же направлении.

Сообщить об ошибке

Представить вектор в форме единичного вектора.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы получить единичный вектор, направленный в том же направлении, что и исходный вектор , мы делим вектор на модуль вектора.

Для , величина:

 .

 Это означает, что единичный вектор в том же направлении  равен, 

.

Сообщить об ошибке

Найти единичный вектор числа

.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти единичный вектор u заданного вектора v , мы следуем формуле

Пусть

Модуль v следует формуле

9017

Для этого вектора в задаче

.

Следуя формуле единичного вектора и заменяя вектор и величину

.

Как таковой,

.

Сообщить об ошибке. Объяснение:

Чтобы найти единичный вектор u заданного вектора V , мы следуем за Формулой

LET

Величина V следует за Формулой

для этого вектора в задаче

9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000

9000 3

. подстановка вектора и величины

Как таковая,

Сообщить об ошибке

Уведомление об авторских правах

Посмотреть Pre-Calculus Tutors

Leonard
Сертифицированный преподаватель

Университет штата Флорида, бакалавр наук, наука об окружающей среде.

View Pre-Calculus Tutors

Erik
Сертифицированный преподаватель

Университет Иллинойса в Урбане-Шампейне, бакалавр наук, физика. Калифорнийский университет в Сан-Диего, магистр наук…

Просмотреть репетиторов по математике

Кристофер
Сертифицированный репетитор

Университет штата Аризона, бакалавр наук, математика.

Все ресурсы для предварительного расчета

12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Learn by Concept

Модуль 24 — Векторы — Урок 1

В этом уроке вы научитесь определять векторы на TI-89 и выполнять три типа умножения векторов. Будут обсуждаться единичные векторы и будут определены два формата, используемые для обозначения векторов.

---

Определение векторов

Величины, которые имеют как величину, так и направление, называются векторами и часто представляются направленными отрезками, как показано ниже.

Показанный вектор имеет начальную точку в точке O и конечную точку в точке P .

Представление векторов с помощью скобок

Векторы можно представить на TI-89, задав координаты кончика стрелки. Например, вектор, идущий из начала координат в точку (3, 2), представлен на ТИ-89 обозначением [3, 2]. Обратите внимание на использование квадратных скобок вместо круглых, чтобы обозначить, что величина является вектором.

• Выполнить NewProb
• Сохраните вектор [3, 2] в переменной и на вашем TI-89
скобки стоят над а также ключи.

ti.com/images/online_courses/t3/calculus/images/pd/CautionBackground.gif»> Вам нужно ввести «запятую» между компонентами при вводе вектора на TI-89, но калькулятор не отображает ее при отображении векторов. Этот факт иллюстрируется приведенным выше снимком экрана.

Определение единичных векторов i и j

Вектор i имеет длину в одну единицу и указывает вдоль положительной оси x , а вектор j имеет длину в одну единицу и указывает на положительную ось y . Поскольку векторы i и j имеют длину в одну единицу, они называются единичными векторами. И i , и j показаны ниже вместе с вектором [3, 2].

Представление векторов с помощью i и j

Другая запись использует единичные векторы i и j для представления вектора. Вектор [3, 2] также можно записать в виде

a = 3 i + 2 j

Обратите внимание, что a , i и j выделены жирным шрифтом, чтобы показать, что они являются векторами.

Нахождение длины вектора

Длина или величина любого вектора a = [x, y] равна

Длина a = [3, 2] есть единицы.

Умножение векторов

Есть три типа умножения, которые включают векторы. Два типа производят вектор, а оставшийся тип производит действительное число. Каждый тип умножения обсуждается ниже.

Скалярное умножение векторов

Сдача c представляют собой

Скаляр — это действительное число. У него есть величина, но нет направления.

скаляр и a представляют собой вектор, скалярное число , кратное c a , является вектором, длина которого равна |c| раз больше длины a , и направление которого совпадает с направлением a , если c положительно, и направлением, противоположным a , если c отрицательно.

Координаты c a находятся путем умножения каждой координаты а по с .

c a = c [ a ₁ , a ₂ ] = [ ca ₁ , ca ₂ ]

• Сохраните вектор [3, -1] в переменной a на вашем калькуляторе и умножьте вектор на скаляр 2.

• Умножьте вектор [2, -5] на скаляр 3, не сохраняя вектор в переменную.

Использование команды unitV

Вектор, который указывает в том же направлении, что и на , и имеет модуль, равный единице, можно найти с помощью команды unitV .

Определите единичный вектор, который указывает в том же направлении, что и a = [3, 2].

• Откройте меню Math, нажав
• Откройте подменю Matrix, выбрав 4:Matrix и нажав
• Прокрутите до L:Векторные операции

Нажатие в то время как в верхней части меню отображается нижняя часть меню, что может быть быстрее, чем прокрутка вниз до нижней части меню.

• Откройте подменю векторной операции, нажав

Пункт меню «1:unitV(» должен быть выделен.

• Нажимать чтобы вставить его в строку редактирования
• Введите единицу измеренияV(а)

Каждый компонент a был умножен на величину, обратную величине a , чтобы создать единичный вектор, который указывает в том же направлении, что и a . Обратите внимание, что дроби были

Рационализация (знаменатель): дробь рационализируется путем записи ее в виде эквивалентной дроби без радикалов в знаменателе.

рационализировано.

Нахождение скалярных произведений векторов

Второй тип умножения называется скалярным произведением . Точечный продукт двух векторов [ A ₁ , A ₂ ] и [ B ₁ , B ₂ ] — A ₂ ] — B ₂ ] — B ₂ ] B ₂ ] B ₂ ] B ₂ ] B ₂ ] — B ₂ ]. б ₁ + а ₂ · б ₂ .
Скалярное произведение a и b можно найти с помощью команды dotP , которая находится в меню Math Matrix :Vector ops.

• Сохраните вектор -2 i + 5 j в b

Вычислите скалярное произведение a · b .

• Откройте подменю «Матрица» в меню «Математика».
• Откройте подменю :Vector ops подменю Matrix.

• Вставьте точку P( в строку редактирования
• Введите точкуP(a,b)

Скалярное произведение a · b равно 4.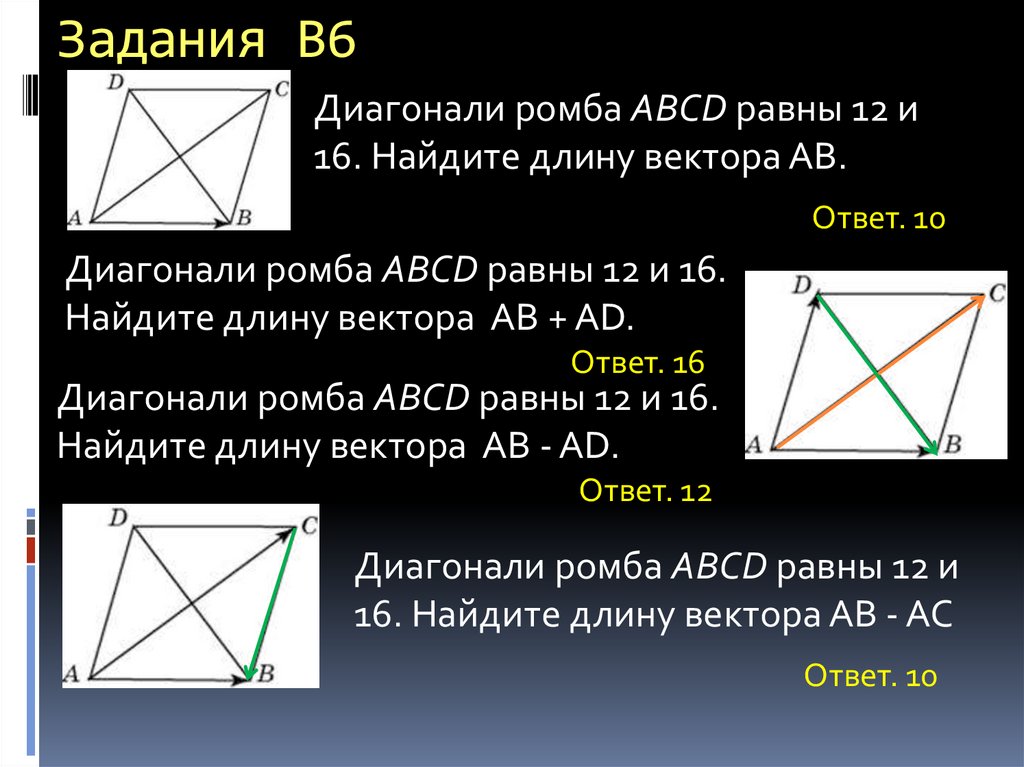

Обратите внимание, что результатом скалярного произведения двух векторов является число 9.0012 реальное число , а не вектор. Скалярное произведение равно произведению величины a , величины b и косинуса угла между a и b .
Если угол между a и b

Скалярные произведения широко используются в физике. Например, они используются для расчета работы силы, действующей на объект.

Проецирование одного вектора на другой вектор

Проекцию можно рассматривать как тень одного вектора на другой. Когда два вектора имеют одну и ту же начальную точку, проекция b на a параллельна a и имеет длину тени b . На приведенной ниже диаграмме показана проекция b на a , записанная как proj 9.0615 a b и показан более темным вектором.

Проекции и скалярные произведения

Величина проекции b на a , |proj _a b |, также называется компонентой b вдоль a , и она равна | б | потому что . Обратите внимание, что компонент b вдоль a равно a · b / | и |.

Поиск формулы для скалярных произведений на вашем калькуляторе

Формула для нахождения скалярного произведения двух векторов [ a ₁ , a ₂ ] и [ b ₁ , b ₂ , b 2 ] может быть получена на TI 9.

• Введите точкуP([a1,a2],[b1,b2])

24.1.1 Напишите формулу для нахождения скалярного произведения двух векторов. Щелкните здесь, чтобы получить ответ.

Определение перекрестных произведений

Третий тип умножения называется перекрестным произведением на и используется в геометрии и во многих случаях в физике и технике. Перекрестное произведение a x b двух трехмерных векторов является вектором, который перпендикулярен к обоим a и b . Если угол между a и b , тогда длина a x b определяется выражением

Перекрестное произведение определено только для трехмерных векторов, но TI-89 вычисляет перекрестное произведение двумерных векторов, рассматривая их как трехмерные векторы с 0 в качестве третьего компонента.

Поиск перекрестных произведений

Перекрестное произведение можно рассчитать с помощью команды crossP , которая находится в меню операций Math Matrix Vector.

Найдите векторное произведение a x b ранее определенных векторов a = [3, 2] и b = [-2, 5].

• Введите crossP(a,b)

[3, 2, 0] x [-2, 5, 0] = [0, 0, 19] = 0 i + 0 j + 19 k

Результатом перекрестного произведения является вектор , который имеет три компонента, что означает, что это трехмерный вектор. Единичный вектор k указывает вдоль положительной оси z. Вектор 0 i + 0 j + 19 k указывает вверх вдоль положительной оси z и имеет длину 19.

Векторное произведение двух векторов a и b всегда перпендикулярно каждому из двух векторов. Его величина равна величине a , умноженной на величину компонента b , который перпендикулярен a .

24.1.2 Найдите векторное произведение трехмерных векторов a = 2 i + j — 4 k и b = — i 2 j + k . Опишите взаимосвязь между и , b и их векторным произведением. Нажмите здесь, чтобы проверить свой ответ.

MathScene — Векторы — Урок 1

MathScene — Векторы — Урок 1

2008 Расмус Эф и Джанн Сак

 

Урок 1

Сложение и вычитание векторов.

Векторы, умноженные на константу.

---

Немного такие величины, как температура и длина, могут быть описаны с помощью одного числа указать их величину. Такие величины называются скалярными.
Другие величины, такие как силы и скорость, также нуждаются в направлении. величина. Они называются векторами. Вектор не обязательно фиксирован в пространстве. Перемещение на 5 м на север по горизонтальной плоскости — одно и то же действие, где бы оно ни находилось. выполненный.

В математические векторы рисуются в виде отрезков со стрелкой. Длина линия представляет величину вектора и направление линии представляет направление вектора.

За например, перевод 5 м на север может быть представлен вертикальной линия длиной 5 см со стрелкой, указывающей вверх (север). Перевод 2 м восток можно изобразить горизонтальной линией длиной 2 см, указывающей вправо. (см. векторы  и в схему).

Вектор представляет собой направленный отрезок, обозначенный стрелкой в ​​конце отрезок в нужном направлении. Длина линии сегмент представляет величину вектора.

Векторы пишутся в текстах маленькими буквами с чертой или стрелкой над их. Если вектор начинается в точке А и заканчивается в точке Б, его часто пишут в качестве (с линию или стрелку). Векторы одинаковой длины и направление равны. Вектор не зависит от его положения в система координат.

На диаграмме ниже линейные векторы AE, FK и DH имеют одинаковую длину. и направление, и все они могут быть помечены как вектор. Если мы рисуем векторы BF, CG, EJ, GL и  NM , они также могут быть помечены как вектор .

В диаграмма вектор (начинается в L и заканчивается в G) параллелен вектору но указывает в противоположном направлении. Мы можем назвать вектор −.

В настоящее время посмотреть на дополнительные возможности.

Если направленная линия AE представляет вектор   , тогда линия в том же направлении, но вдвое длиннее вектор 2.
Точно так же, если направленная прямая BD представляет вектор затем ГГ, что составляет половину длины BD, должно быть ∙.

Наши результаты можно резюмировать следующим образом

Умножение вектора на постоянное число влияет только на длину, а не на направление. Если число отрицательное, направление вектора перевернутый.

Эти результаты показаны на диаграмме ниже, где мы объединили два направленных отрезки вместе, оба представляют вектор .

Это логично сделать вывод, что  +  это одно и то же как 2. Это не поэтому удивительно видеть, что сложение двух векторов вместе выполняется путем соединения их вместе так, чтобы голова одного соединилась с хвостом другого.

В на приведенной выше диаграмме направленная линия AE представляет вектор  и KM вектор . БК это параллельно AE, но в два раза длиннее. Соединяя вместе БК (2) и КМ (), имеем сделал вектор 2+ представлены по БМ.

Добавление двух векторов включает в себя их объединение так, чтобы второй вектор начинался где заканчивается первый вектор. Тогда сумма двух векторов равна направленный отрезок, идущий от начала первого вектор в конец второго.

---

 

Пример 1:

в диаграмма ниже, AE представляет вектор, переменный ток вектор а также АМ вектор .

как мы можем написать, используя а также ?
Мы можем сделать это, удвоив   (путем добавление вектора EJ к AE), а затем добавление 1 к этому. ЭйДжей + Дж. М. (См. схему).

Результат:   = 2 .  + 1 .

Эта операция называется нахождением компонент вектора   через а также . компоненты 2 и 1 .

---

Пример 2:

Теперь мы используем те же координатные точки, что и в примере 1, чтобы найти направленную линию который может представлять − .

 

Начнем с предположения, что − то же самое вектор как   + (- ).

Нам нужно больше места на нашей диаграмме, поэтому мы нарисуем вектор с G как его отправная точка. Это дает нам GL.

Затем мы добавляем вектор, который имеет ту же длину, что и но указывает в обратном направлении, это LJ. Нашей отправной точкой была G, и мы закончили в J, поэтому результирующий перевод происходит из G в J, что дает вектор = − .

 

На приведенной выше диаграмме показано, что , взяты из конец и к концу из , тот же вектор, что и а также поэтому также равно − . Это дает Нам второй метод для нахождения разницы между двумя векторами.

Разница между двумя векторами, − может быть найдено изменением направления вектора и добавление его в вектор . Его также можно найти, рисуя а также так, что они начать с той же точки. затем − это вектор, который идет от конца до конца из .

Тот факт, что вектор представлен длинами и направлениями (углами) означает, что нам часто приходится использовать тригонометрию для решения векторных задач, для пример для вычисления длины и направления суммы или разности два вектора.

Обычно используется символ абсолютного значения, когда речь идет о длина вектора.

 

длина вектора пишется ||.

---

Пример 3:

В строительной отрасли инженеры и архитекторы должны уметь рассчитывать действие сил, которые взаимодействуют в разных частях здания. Представьте, что векторы на приведенной ниже диаграмме представляют собой силы, действующие на тот же объект. Нам нужно выяснить, каков будет общий эффект.

Сначала мы используем сложение векторов, чтобы сложить их вместе.

Добавленные векторы заканчиваются на единицу ниже начальной точки. Это означает, что Эффект всех четырех сил заключается в том, чтобы притянуть объект, на который они действуют, на одну единицу вертикально вниз. Другими словами, сила в одну единицу, направленная вертикально вниз, точно тот же эффект, что и остальные четыре силы вместе взятые.

---

Пример 4:

Используя те же векторы, что и в примере 3, найдите вектор  – −  + .

Мы меняем направление а также а потом соедините все вектора вместе.

Результат – красный вектор на диаграмме, проведенный из начального точки первого вектора до конца четвертого. Это подчеркивает факт что положение векторов не имеет значения, только длина и направление должны оставаться неизменными. На самом деле нам вообще не нужно использовать систему координат. на данном этапе он используется для облегчения правильного рисования векторов.

---

Пример 5:

Корабль плывет на север со скоростью 24 морских мили в час (узлы). Сильное океанское течение со скоростью 7 узлов с запада течет прямо по всему кораблю. Какова фактическая скорость и направление движения корабля относительно на дно океана? Сначала нарисуйте два вектора и добавьте их вместе. Цифры 24 и 7 образуют стороны прямоугольного треугольника. где гипотенуза показывает действительную скорость и направление движения корабля. Если мы назовите начальную точку A и конечную точку B, затем | | это реальная скорость корабля и угол между АВ и вертикалью, назовите это A даст нам угол, на который повернули корабль ( подшипники). Использование Pythagoras для поиска ||:

| | мы можем найти с помощью Пифагора.

| | ² = 24 ² + 7 ²

= 576 + 49 = 625

| | знак равно

= 25 Узлы.

Мы найдите угол А, используя правило для загара:

tan A = противоположная сторона/прилегающая сторона.

= 7/24

A = загар ⁻¹ (7/24) ≈ 16

---

Пример 6:

Паром должен пересечь реку шириной 100 м. Лодка может плыть со скоростью 3 м/с. и река течет со скоростью 1 м/с.

а) Как много времени потребуется парому, чтобы пересечь реку, если он не попытается противодействовать эффекту течения рек?

Мы можем игнорировать течение реки, так как паром не пытается работать. против течения. Нам просто нужно рассчитать, сколько времени потребуется, чтобы путешествовать 100м. со скоростью 3 м/с.

       Время =  100 м/3 м/с = 33⅓ с

б)   Рассчитайте фактическую скорость лодки.

На диаграмме показаны паром и река, а также то, что происходит, когда мы складываем их векторы вместе.

x показывает реальную скорость парома. используя Пифагора, мы получаем:

х ² = 3 ² + 1 ² = 9 + 1 = 10

х = ≈ 3,2 м/с

c) Какое расстояние вниз по реке прошел паром после пересечения реки?

В этом случае x представляет собой расстояние, которое нам нужно вычислить, а 100 – ширина реки. Они образуют короткие стороны прямоугольного треугольника. Этот треугольник подобен (в тех же пропорциях), что и предыдущая диаграмма. поэтому мы можем использовать коэффициенты для вычисления x.

1/3 = х/100

Умножить на 100.

х = 100/ 3 = 33⅓ м

Мы использовали векторы для решения этой задачи, но на самом деле это простая легко решаемая геометрическая задача.
Мы знаем, что путешествие занимает 33⅓ с и что река двигает паром. вниз по течению 1 м каждую секунду. Отсюда следует, что за 33⅓ с паром перемещается на 33⅓ м вниз по течению.

г)   Паромщик желает приземлиться на берегу прямо напротив того места, где он начал путешествие. В каком направлении ему нужно двигаться, чтобы противодействовать эффекту течения рек?

Он должен направить лодку вверх по течению так, чтобы на каждые 3 метра, которые он путешествии река уводит его на 1 м вниз по течению. Мы называем угол y и используем правило для синуса, чтобы найти у .

г = sin ⁻¹ (1/3) ≈ 19,5

e)   Рассчитайте фактическую скорость лодки, когда она меняет направление находится в г).

Фактическая скорость лодки обозначается x м/с и находится путем сложения векторы длины 3 и длины 1 вместе

(см. схему ниже). х — одна из коротких сторон прямоугольного треугольник, поэтому мы можем использовать триггерные функции или Пифагора для вычисления Икс.

Воспользуемся правилом Пифагора.

х ² + 1 ² = 3 ²

х ² = 9 — 1 = 8

Икс = 8 ≈ 2,8 м/с

---

Пример 7:

Тяжелые сани тянут с помощью двух отрезков веревки, привязанных к передней части сани и которые составляют угол 60 между ними.

No related posts.