Взаимно обратные функции: алгоритм вывода формулы, примеры
- Функция, обратная данной
- Алгоритм вывода формулы функции, обратной данной
- Свойства взаимно обратных функций
- Примеры
Функция, обратная данной
По определению (см. §34 справочника для 7 класса)
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Пусть некоторое соответствие задано таблицей:
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
Множество значений X = {-4;-3;…;4} отображается в множество значений Y = {-2;-1,5;…;2}: $X \xrightarrow{f} Y$.
Например: аналитическое выражение для функции $X \xrightarrow{f} Y$, заданной таблицей $y = f(x) = \frac{x}{2}$. Обратное соответствие $Y \xrightarrow{g} X$ также является функцией x = g(y) = 2y.
Функция g — обратная функция к f.
В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = \frac{x}{2}$ и y=2x являются взаимно обратными.
Алгоритм вывода формулы функции, обратной данной
На входе: множества X и Y, для которых оба соответствия $X \xrightarrow{f} Y$ и $Y \xrightarrow{g} X$ являются функциями.
Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x \rightarrow y$, $y \rightarrow x$.
Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.
Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.
Например:
1) Пусть исходная функция $y = \frac{x}{2}$
Шаг 1.
2+1$
Шаг 2. Находим y из полученной формулы: $y = \sqrt{\frac{x-1}{2}}$ — искомая обратная функция
Шаг 3. На обратную функцию накладываются ограничения
на $x:x-1 \ge 0 \Rightarrow x \ge 1$, на $y:y \ge 0$
Тогда исходная функция определяется на множествах $y \ge 1$, $x \ge 0$
Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.
Свойства взаимно обратных функций
Пусть f и g — взаимно обратные функции. Тогда:
1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.
3. Если f — нечётная, то и g — нечётная.
4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.
5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.
Например:
Графики пар взаимно обратных функций, найденных выше:
Примеры
Пример 1.
Задайте формулой функцию, обратную данной.
а) y = 5x-4
Меняем аргумент и значение: x = 5y-4
Получаем: $y = \frac{x+4}{5}$ — искомая обратная функция
б) y = -3x+2
Меняем аргумент и значение: x = -3y+2
Получаем: $y = \frac{-x+2}{3}$ — искомая обратная функция
в) y = 4x+1, где $-1 \le x \le 5$
Меняем аргумент и значение: x = 4y+1
Получаем: $y = \frac{x-1}{4}$
Требуем, чтобы: $-1 \le y \le 5 \Rightarrow -1 \le \frac{x-1}{4} \le 5 \Rightarrow -4 \le x-1 \le 20 \Rightarrow -3 \le x \le 21$
Итак, искомая обратная функция: $y = \frac{x-1}{4}$, где -3 $\le x \le 21$
г) $y=- \frac{1}{2} x+7$, где $2 \le x \le 9$
Меняем аргумент и значение: $x=-\frac{1}{2} y+7$
Получаем: y = 2(-x+7) = -2x+14
Требуем, чтобы: $2 \le y \le 9 \Rightarrow 2 \le -2x+14 \le 9 \Rightarrow -12 \le -2x \le -5 \Rightarrow$
$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$
$y = -2x+14,где 2,5 \le x \le 6$ — искомая обратная функция
Пример 2.
2+3$
Область определения: $x \ge 1$
Область значений: $y \ge 3$
найти уравнение обратной у=3х+2
Обратный ДЕЙЛ Л.
найти уравнение обратного y=3x +2
Подписаться І 5
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Григорий С. ответил 24.02.13
Репетитор
0 (0)
Сертифицированный учитель физики и математики G.S.
Смотрите таких репетиторов
Смотрите таких репетиторов
Все ответы правильные. Только одно добавить. Если у вас есть одна функция (скажем, f(x) = 3x+2), и вам нужно найти ее обратную функцию g(x), вы можете начать со свойства композиции: f(g(x)) = x, что означает
f(g) = 3g +2 = x
Тогда вы можете найти d и найти g = (x-2)/3 или g = (1/ 3)х -2/3 (в наклоне-перехвате форма).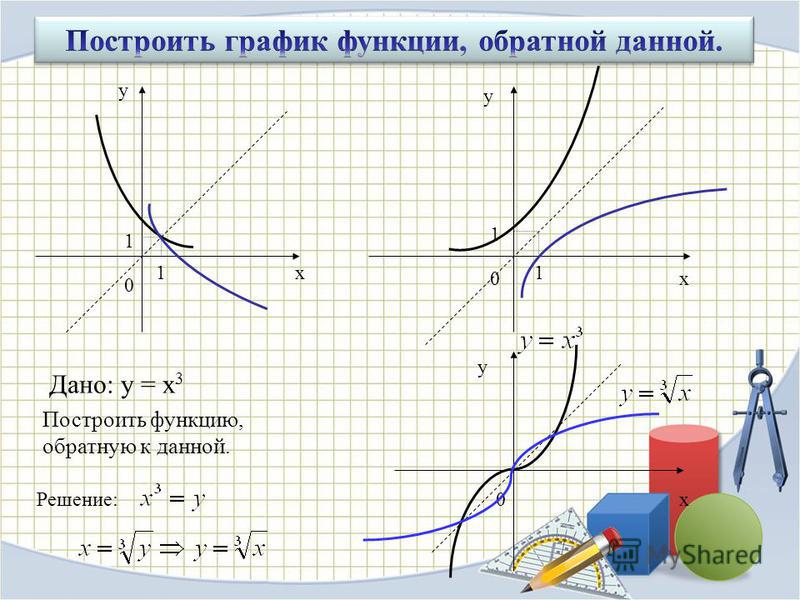
Уравнение f(g(x)) = x означает, что две функции, f(x) и g(x), симметричны относительно прямой
y = x (она работает как биссектриса). Вы увидите это, если построите оба графика на одной координатной плоскости.
Голосовать за 1 Понизить
Подробнее
Отчет
Рейна Х. ответил 24.02.13
Репетитор
0 (0)
Любовь к математике, страсть к преподаванию. CSUSB Математический майор.
Смотрите таких репетиторов
Смотрите таких репетиторов
Сладко! Таким образом, инверсии звучат довольно интенсивно, когда вы впервые смотрите на них, но на самом деле это довольно просто
Первый шаг к нахождению обратного уравнения — это поменять местами x и y.
хотите y сам по себе, поэтому мы вычитаем на 2: 3y=x-2
теперь мы делим на 3: y= (x-2)/3
если ваш учитель хочет это в виде уравнения (y=mx+b) вы просто переписываете его:
y= x/3 -2/3, что совпадает с y= 1/3 x — 2/3 (где наклон равен 1/3, на всякий случай, если вы хотите знать :))
Надеюсь, это помогло Дейлу!
Голосовать за 1 Понизить
Подробнее
Отчет
Наталия Д. ответил 24.02.13
Репетитор
Новое в Византе
Терпеливый и эффективный репетитор по самому сложному предмету.
Смотрите таких репетиторов
Смотрите таких репетиторов
Решим функцию y = 3x + 2 относительно «x» —-> 3x = y — 2 —-> x = (y — 2)/3
просто «поменяем» местами «y» и » x» и получим обратную функцию для данного
y = (1/3)x — 2/3
Голосовать за 1 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
