Найдите координату середины отрезка соединяющего точки: Найдите координату середины отрезка, соединяющего точки : а) 1 и 7 б) 3 и 8…

Координаты | ЕГЭ по математике (профильной)

Русский язык Математика (профильная) Обществознание Физика История Биология Химия Английский язык Информатика Литература

Задания Варианты Теория

Округление Проценты Операции с числами Графики Диаграммы Векторы Линейные, квадратные, кубические уравнения Рациональные уравнения Иррациональные уравнения Показательные уравнения Операции со степенями Логарифмические уравнения Тригонометрические уравнения и преобразования Преобразование логарифмических выражений Преобразование иррациональных выражений Преобразование рациональных выражений Задачи с физическим смыслом Задачи на прогрессии и проценты (включая часть С) Задачи на движение по прямой и по окружности Задачи на движение по воде Задачи на производительность труда Окружности и её элементы Координаты Треугольник Четырехугольники и многоугольники Задачи на координатной сетке Прямоугольные треугольники Равнобедренные треугольники Треугольники общего вида Четырехугольники Касательные, секущие, хорды Вписанные и описанные окружности Теория вероятностей Производная Наибольшее и наименьшее значение функции Первообразная Куб Прямоугольный параллелепипед Призма Пирамида Многогранники Комбинации тел Цилиндр, конус, шар Уравнения, часть С Планиметрия, часть С Стереометрия, часть С Неравенства, часть С Параметрические уравнения, неравенства и системы, часть С Задача повышенной сложности, часть С

Разбор сложных заданий в тг-канале:

Посмотреть

Координатная плоскость состоит из двух взаимно перпендикулярных координатных прямых. Началом отсчета на обеих прямых принято считать точку их пересечения (точку $О$). Горизонтальная ось $О_х$ называется абсциссой, вертикальная ось $О_у$ — ординатой.

У каждой точки на плоскости есть две координаты, в скобках на первом месте всегда стоит координата $Х$, на втором $Y$, например $М(2;3)$ – читается: точка $М$ имеет координату $х=2$, координату $у=3$.Симметрия точек относительно осей координат:

1. У точек, симметричных относительно оси $О_х$ абсциссы совпадают, а ординаты являются противоположными числами.
2. У точек, симметричных относительно оси $О_у$ ординаты совпадают, а абсциссы являются противоположными числами.

Векторы и отрезки в координатах:

1. Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.

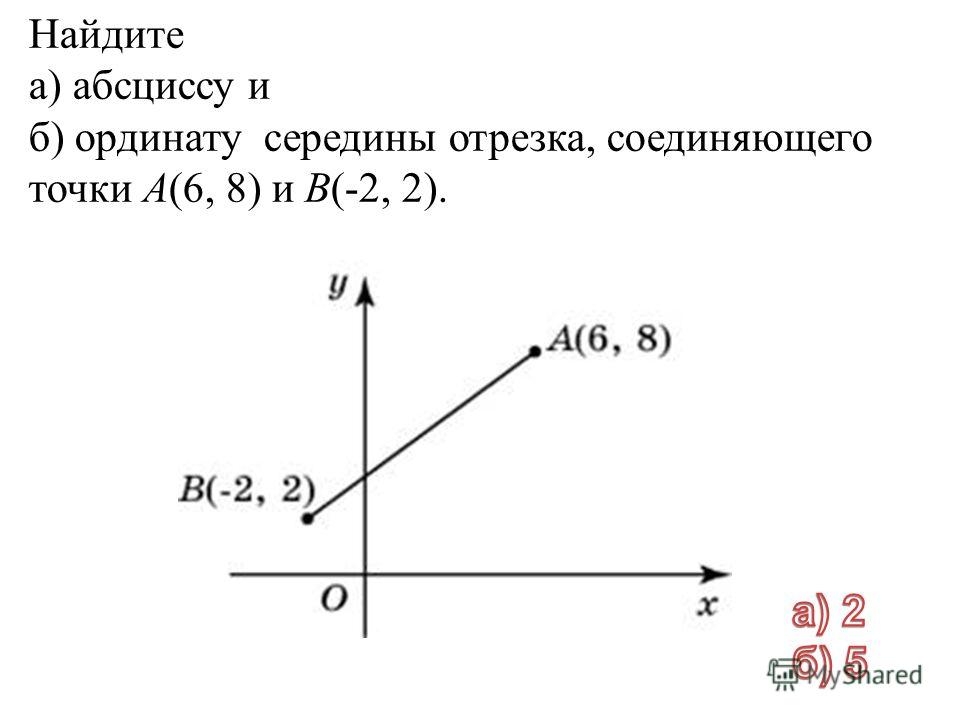
2. Координаты середины отрезка (вектора) равны среднему арифметическому координат его концов.

Пример:

Найдите абсциссу середины отрезка, соединяющего точки $В(2;8)$ и $A(6;4)$.

2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Пример:

В прямоугольном треугольнике $АВС$ для острого угла $В$:

$sin ⁡B={AC}/{AB};$

$cos ⁡B={BC}/{AB};$

$tg B={AC}/{BC};$

$ctg B={BC}/{AC}.$

Признаки подобия треугольников:

1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Практика: решай 3 задание и тренировочные варианты ЕГЭ по математике (профильной)

математика (база): Задачи на координатной сетке

Рассмотрим прямоугольную систему координат Oxy (см. рис. 207). Длина отрезка AB, для которого известны координаты его концов A(xA; yA) и B(xB; yB), определяется по формуле

 Координаты середины отрезка вычисляются по формулам:

 Если точки A и B симметричны относительно оси Ox (оси абсцисс), то их ординаты противоположны (см. рис. 208), а абсциссы равны: A(x; y), B(x; −y).
 Если точки A и C симметричны относительно оси Oy, то их абсциссы противоположны, а ординаты равны: A(x; y), C(−x; y).
 Если точки A и D симметричны относительно начала координат, то их координаты противоположны: A(x; y), D(−x; −y).

 Координаты и векторы в пространстве
 1. Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.


 4. Любой вектор можно единственным образом разложить по трём некомпланарным векторам.

 9. Координаты середины отрезка равны средним арифметическим координат его концов.

 10. Свойства скалярного произведения векторов:

  

Задачи с решениями

 Найдите расстояние от точки B с координатами (12; −5) до начала координат (см. рис. 209)

 Решение.

 Ответ: 13.

---

 Найдите абсциссу точки, симметричной точке A(2; 5) относительно оси Oy (см. рис. 210).

 Решение.
 Точке A симметрична точка B(−2; 5) (см. рис. 211). Абсцисса точки B равна −2

 Ответ: -2.

---

 Найдите ординату середины отрезка, соединяющего точки A(−4; 6) и B(2; 4) (см. рис. 212).

 Решение.

 Ответ: 5.

---

 Точки A(−1; −2), B(4; −1), C(6; 5) и D являются вершинами параллелограмма. Найдите абсциссу точки P пересечения его диагоналей (см. рис. 213).

 Решение.

 Ответ: 2,5

---

 Найдите ординату центра окружности (см. рис. 214), описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (2; 2), (2; −6), (−4; −6), (−4; 2)

 Решение.

 Ответ: -2

---

 Точки O(0; 0), B(8; 2), C(0; 8) являются вершинами параллелограмма (см. рис. 215). Найдите ординату точки M

 Решение.
 Ордината — это координата по оси Oy. Она равна длине отрезка HM (см. рис. 216). HB = 2, так как ордината B равна 2. Поскольку противоположные стороны параллелограмма равны, то OC = BM = 8. Тогда HM = 2 + 8 = 10

 Ответ: 10

---

 Прямая a проходит через точки с координатами (0; 2) и (−4; 0). Прямая b проходит через точку с координатами (0; −4) и параллельна прямой a (см. рис. 217). Найдите абсциссу точки пересечения прямой b с осью Ox.

 Решение.

 1-й способ.

 Нарисуем картинку на клетчатой бумаге (см. рис. 218).

 Абсцисса точки пересечения прямой b с осью Ox равна длине отрезка OA. Так как прямые параллельны, углы HCO и ABK равны, достроим 2 треугольника BKT и TMA, равных треугольнику HCO.
 OA = BK + TM = 4 + 4 = 8.

 Ответ: 8.

 2-й способ.

 Треугольники CHO и BOA подобны по трём углам (см. рис. 219), значит, их стороны пропорциональны. OB : OH = OA : OC, тогда 4 : 2 = OA : 4. OA = 8.

 Ответ: 8

---

 Найдите угловой коэффициент прямой, проходящей через точки с координатами (12; 0) и (0; 12) (см. рис. 220).

 Решение.

 1-й способ.

 Угловой коэффициент прямой равен тангенсу угла, который прямая образует с положительным направлением оси Ox (там, где на оси стрелочка). В нашей задаче это угол a (см. рис. 221).

 Ответ: -1

 2-й способ.

 Ответ: -1

Как найти середину отрезка

Все ресурсы по промежуточной геометрии

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

Промежуточная помощь по геометрии » Координатная геометрия » Линии » Формула середины » Как найти середину отрезка

Что такое середина между и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Середина определяется путем взятия среднего значения координат и по отдельности.

Пусть и

Таким образом, формула средней точки становится и

Таким образом, средняя точка равна

Сообщить об ошибке

Какова середина отрезка, соединяющего точки и

Возможные ответы:

Правильный ответ:

Объяснение:

Используйте формулу средней точки:

Сообщить об ошибке

Даны две точки  и  и отрезок, соединяющий их.

Что такое середина отрезка? Кроме того, какова длина отрезка?

Возможные ответы:

Средняя точка:

Длина:

Средняя точка:

Длина:

Средняя точка:

Длина:

Средняя точка:

Длина:

Средняя точка:

Длина:

Правильный Ответ:

Midpoint:

Длина:

. Объяснение:

Формула средней точки выглядит следующим образом:

Это имеет смысл; это так же просто, как среднее значение компонентов и каждой точки.

Для этой задачи .

Итак, середина равна

 

Формула расстояния выглядит следующим образом:

Порядок, в котором вы ставите первый и второй компоненты каждой точки, НЕ имеет значения, когда положительное или отрицательное число возводится в квадрат, оно всегда будет положительным.

 

Таким образом, расстояние равно

Сообщить об ошибке

Найдите середину отрезка, идущего от  до .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти середину отрезка, необходимо найти среднее значение значений x и среднее значение значений y.

Наши значения x равны  и  чтобы найти их среднее значение, мы делаем это.

Наши значения y равны и , поэтому наше среднее значение равно . Следовательно, наша средняя точка должна быть .

Сообщить об ошибке

Найти координату середины отрезка, соединяющего пару точек

 и .

Возможные ответы:

Невозможно определить

Правильный ответ:

Пояснение:

Координата середины отрезка, соединяющего пару точек, равна

Итак, для пары точек и,

получаем:

Сообщить об ошибке

Найти координату точки середина отрезка, соединяющего пару точек

 и .

Возможные ответы:

Невозможно определить

Правильный ответ:

5

5 Объяснение:

Координата середины отрезка, соединяющего пару точек, равна

.

Таким образом, для пары точек  и 

мы получаем

Сообщить об ошибке

Линия проходит от начала координат до . Какова его середина?

Возможные ответы:

Правильный ответ:

Объяснение:

Исходной точкой является точка. Мы можем использовать обычную формулу средней точки с as и заданной точкой как :

 

Обратите внимание, что, поскольку первая точка является исходной, мы усредняем эти точки с 0 или, другими словами, просто делим на 2.

Сообщить об ошибке

Между двумя точками (5, 10) и (3, 6) есть отрезок. Какая формула даст вам правильную середину отрезка?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти среднюю точку по двум точкам на координатной плоскости, вы в основном находите среднее значение значений x и среднее значение значений y. Для этого следуйте приведенной ниже формуле:

С нашими точками это дает:

Сообщить об ошибке

Линия имеет конечные точки в точках (4,5) и (-6,8). Где его середина?

Возможные ответы:

Правильный ответ:

Объяснение:

Средняя точка — это точка, равноудаленная от каждой конечной точки.

Мы находим его, используя формулу, которая вычисляет среднее значение координат x и y.

Сообщить об ошибке

Сегмент линии имеет конечные точки  и . Какова середина этого отрезка?

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните формулу для нахождения середины отрезка:

Координаты средней точки — это просто среднее значение координат x и среднее значение координат y.

Подставьте заданные точки, чтобы найти середину отрезка.

Сообщить об ошибке

← Предыдущий 1 2 3 Далее →

Уведомление об авторских правах

Все промежуточные ресурсы по геометрии

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

Объяснение урока: Середины и биссектрисы перпендикуляра

В этом объяснении мы научимся находить серединный перпендикуляр к отрезку, определяя его середину и перпендикулярная линия, проходящая через эту точку.

Наша первая цель — научиться вычислять координаты середины отрезка, соединяющего две точки. Предположим, мы даны две точки 𝑃(𝑥,𝑦) и 𝑃(𝑥,𝑦). Середина Отрезок 𝑃𝑃 есть точка 𝑀, лежащая на 𝑃𝑃 ровно посередине между 𝑃 и 𝑃. Это значит, что 𝑥-координата 𝑥 точки 𝑀 лежит на полпути между 𝑥 и 𝑥 и поэтому может быть рассчитана путем усреднения двух точек, что дает нам 𝑥=𝑥+𝑥2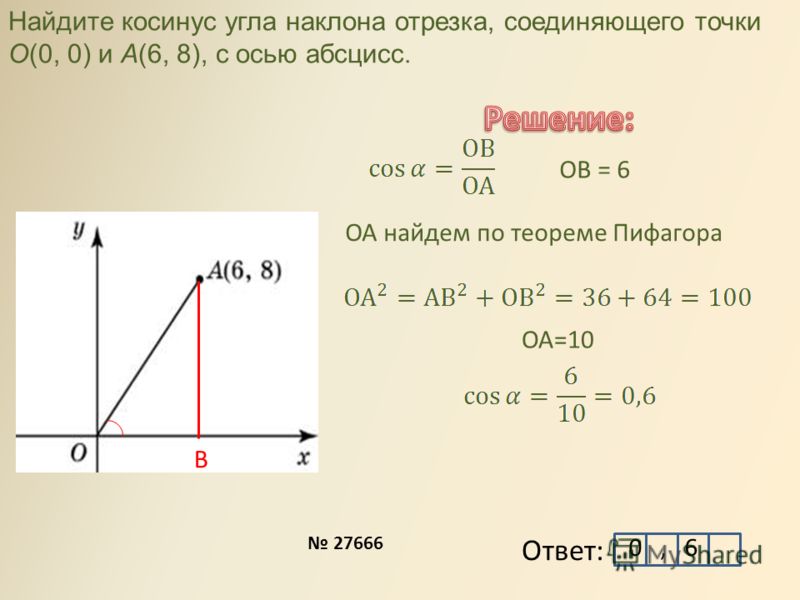. То же верно и для 𝑦-координаты 𝑦 точки 𝑀. Это приводит нас к следующей формуле.

Формула: координаты средней точки

Предположим, что 𝑃(𝑥,𝑦) и 𝑃(𝑥,𝑦) — точки, соединенные линией сегмент 𝑃𝑃. Тогда координаты середины отрезка 𝑃𝑃 даются 𝑀(𝑥,𝑦)=𝑥+𝑥2,𝑦+𝑦2.

Потренируемся находить координаты средних точек.

Пример 1. Нахождение середины отрезка по заданным конечным точкам

Учитывая 𝐴(4,8) и 𝐵(6,6), каковы координаты средней точки из 𝐴𝐵?

Ответ

Напомним, что середина 𝑀 отрезка — это точка на полпути между концами, которую мы можем найти усреднением 𝑥- и 𝑦-координат 𝐴 и 𝐵 соответственно. Таким образом, применяем формулу: 𝑀(𝑥,𝑦)=𝑥+𝑥2,𝑦+𝑦2=4+62,8+62=(5,7).

Следовательно, координаты середины 𝐴𝐵 (5,7).

Мы также можем использовать формулу для координат средней точки, чтобы вычислить одну из конечных точек отрезка, зная его другую конечной точки и координаты середины.

Пример 2. Нахождение конечной точки отрезка прямой по средней точке и другой конечной точке

Начало — середина прямого отрезка 𝐴𝐵. Найдите координаты точки 𝐵, если координаты точки 𝐴 равны (−6,4).

Ответ

Здесь нам дан один конец отрезка и середина 𝑀(0,0) и попросил найти другую конечную точку. Мы можем сделать это, используя формулу средней точки в обратном порядке: 𝑀(𝑥,𝑦)=(0,0)=𝑥+𝑥2,𝑦+𝑦2=−6+𝑥2,4+𝑦2.

Это дает нам два уравнения: −6+𝑥2=0−6+𝑥=0𝑥=6 и 4+𝑦2=04+𝑦=0𝑦=−4.

Мы заключаем, что координаты 𝐵 равны (6,−4).

Одним из приложений вычисления середины отрезков прямой является вычисление координат центров окружностей с учетом их диаметров по той простой причине, что центр окружности является серединой любого из ее диаметров.

В следующем примере мы увидим пример нахождения центра круга с помощью этого метода.

Пример 3. Нахождение центра окружности по конечным точкам диаметра

Точки 𝐴(4,1) и 𝐵(−4,−5) определяют диаметр 𝐴𝐵 круга с центром 𝑀. Найдите координаты 𝑀 и длину окружности, округляя ответ до десятых.

Ответ

Центр 𝑀 круга является серединой его диаметра 𝐴𝐵. Отзывать что середина 𝑀 отрезка (например, диаметра) может быть найдена путем усреднения 𝑥- и 𝑦-координаты концов 𝐴 и 𝐵 следующим образом: 𝑀(𝑥,𝑦)=𝑥+𝑥2,𝑦+𝑦2=4−42,1−52=(0,−2).

Длина окружности находится по формуле 𝐶=2𝜋𝑟, где 𝑟 — длина его радиус. Длина радиуса — это расстояние от центра окружности до любой точки на ее радиусе, например, точка 𝐴(4,1). Мы можем рассчитать эту длину, используя формулу для расстояния между двумя точками 𝑀 и 𝐴: 𝑟=(𝑥−𝑥)+(𝑦−𝑦)𝑟=(0−4)+(−2−1)=16+9=25.

Извлечение квадратных корней , мы находим, что 𝑟=5 и, следовательно, длина окружности равна 2𝜋𝑟=10𝜋=31,4 с точностью до десятых.

Таким образом, координаты центра равны (0,−2), а длина окружности равна 31,4 относительно центра. ближайший десятый.

Обратимся теперь ко второй основной теме этого объяснения, вычислению уравнения серединного перпендикуляра к данному отрезок.

Определение: Биссектрисы перпендикуляра

Дан отрезок 𝐴𝐵, серединный перпендикуляр к 𝐴𝐵 — единственная прямая, перпендикулярная 𝐴𝐵, проходящая через середину 𝐴𝐵.

Напомним, что для любой прямой 𝐿 с наклоном 𝑚 наклон любой перпендикулярной к ней линии равен отрицательная обратная величина 𝑚, то есть −1𝑚. Мы можем использовать этот факт и наше понимание середин отрезков, записать уравнение серединного перпендикуляра к любому отрезку.

Практическое руководство. Вычисление уравнения биссектрисы отрезка

Предположим, что нам дан отрезок 𝑃𝑃 с концами 𝑃(𝑥,𝑦) и 𝑃(𝑥,𝑦) и хотите найти уравнение их серединный перпендикуляр.

1. Сначала мы вычисляем наклон сегмента прямой. Для этого напомним определение наклона: наклон изменениявизменении в наклон биссектрисы = −𝑥−𝑥𝑦−𝑦.
2. Далее находим координаты середины 𝑃𝑃, применяя формулу к конечные точки: 𝑀(𝑥,𝑦)=𝑥+𝑥2,𝑦+𝑦2. 
3. Теперь мы можем подставить эти координаты и наклон в форму уравнения прямой линии, состоящую из точек и наклонов: Это дает нам уравнение для серединного перпендикуляра.

Давайте попробуем применить этот алгоритм.

Пример 4. Нахождение биссектрисы отрезка, соединяющего две точки

Найдите уравнение биссектрисы, соединяющей точки отрезка 𝐴(1,3) и 𝐵(7,11). Дайте ответ в виде 𝑦=𝑚𝑥+𝑐.

Ответ

Чтобы найти уравнение серединного перпендикуляра, нам сначала нужно найти его наклон, который является отрицательной обратной величиной наклон отрезка, соединяющего 𝐴 и 𝐵. Это дается наклон 𝐴𝐵=𝑦−𝑦𝑥−𝑥=11−37−1=86=43.

Теперь мы можем найти отрицательное обратное число, перевернув дробь и взяв отрицательное; это дает нам следующее: наклон биссектрисы = −34.

Далее нам нужны координаты точки на серединном перпендикуляре. Поскольку биссектриса (по определению) проходит через середину отрезка 𝐴𝐵, мы можем использовать формулу для координат середина: 𝑀(𝑥,𝑦)=𝑥+𝑥2,𝑦+𝑦2=1+72,3+112=(4,7). 

Подставляя эти координаты и наш наклон −34 в форму точка–наклон уравнения прямая линия, 𝑦−𝑦=𝑚(𝑥−𝑥)𝑦−7=−34(𝑥−4), и переставляя в виде 𝑦=𝑚𝑥+𝑐, мы имеем 𝑦=−34𝑥+10.

В нашем последнем примере мы будем использовать наше понимание средних точек и серединных перпендикуляров для вычисления некоторых неизвестных значений.

Пример 5. Определение неизвестных переменных, описывающих биссектрису перпендикуляра отрезка

Отрезок 𝐴𝐵 соединяет точки 𝐴(−6,−6) и 𝐵(0,𝑝). Серединный перпендикуляр к 𝐴𝐵 имеет уравнение 𝑦=−3𝑥+𝑐. Найдите значения 𝑝 и 𝑐.

Ответ

Поскольку биссектриса имеет наклон −3, мы знаем, что отрезок 𝐴𝐵 имеет наклон 13 (отрицательная обратная величина −3). Мы можем вычислить 𝑦-координату точки 𝐵 (то есть, 𝑝), используя определение уклона 𝑚: 𝑚=𝑦−𝑦𝑥−𝑥13=𝑝−(−6)0−(−6)=𝑝+662=𝑝+6𝑝=−4.

Вычислим значение 𝑐 в уравнении 𝑦= −3𝑥+𝑐 серединного перпендикуляра используя координаты середины 𝑀 точки 𝐴𝐵 (это точка, которая лежит на серединный перпендикуляр по определению).

У нас есть формула 𝑀(𝑥,𝑦)=𝑥+𝑥2,𝑦+𝑦2=−6+02,−6−42=(−3,−5).

Теперь мы можем заменить 𝑥 =−3 и 𝑦=−5 в уравнение серединного перпендикуляра и переставить, чтобы найти 𝑐: 𝑦=−3𝑥+𝑐−5=−3×−3+𝑐𝑐=−5−9=−14.

Наше решение для примера: 𝑝=−4, 𝑐=−14.

Давайте закончим повторением нескольких важных понятий из этого объяснения.

Ключевые точки

• Мы можем использовать формулу 𝑀(𝑥,𝑦)=𝑥+𝑥2,𝑦+𝑦2 найти координаты середины отрезка, зная координаты его концов. Мы можем использовать ту же формулу для вычисления координат конечной точки с учетом средней точки и другой конечной точки.
• Мы можем вычислить центры окружностей, зная конечные точки их диаметров.
• Мы знаем, что биссектриса отрезка — это единственная прямая, перпендикулярная отрезку, проходящая через его середина.
• У нас есть процедура для вычисления уравнения серединного перпендикуляра к отрезку с заданными координатами его конечные точки:
  1. Сначала мы вычисляем его наклон как отрицательную обратную величину наклона отрезка прямой.

     No related posts.