Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
е.
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.
75 . Найдите АС.
В двузначном натуральном числе сумма цифр равна 13.Число десятков на 3 больше числа единиц. Найдите это число.
треугольник авс вписан в окружность ДА касательная угол с = 59 , угол в = 93. найти угол АДС
Решено
1. Изобразите при помощи кругов Эйлера отношения между множествами А и В:
Решено
основание прямой призмы ромб с острым углом 60градусов.боковое ребро призмы 10см а площадь боковой поверхности 240см в квадрате найдите площадь…
Пользуйтесь нашим приложением
Как найти координаты середины отрезка
Основное определение отрезка
Определение
Отрезок — это прямая линия, которая соединяет две произвольно расположенные точки, именуемые окончанием отрезка. В качестве конкретного примера можно назвать точки A и B и соответственно отрезок AB.
Прямую АВ можно получить путем удлинения отрезка, который состоит из двух точек. Вследствие чего, можно сказать, что полученный отрезок АВ — это часть прямой, которая ограничена точками А и В. Отрезок объединяет обе точки, которые являются концами прямой, а также множество других точек, лежащих на отрезке.
Например: дана точка К которая расположена между заданными отметками, следовательно, можно сказать, что данная точка лежит на этом отрезке.
Определения
Длина прямой – конкретное отмеренное расстояние, которое задано в масштабе. Чаще всего данный параметр задается как АВ.
Середина отрезка – это некая определенная отметка, которая лежит на прямой и удалена от концов на одинаковом расстоянии друг от друга. Ее можно обозначить как координата С.
Середина отрезка на координатной прямой
Заданы следующие параметры: координатная прямая Ox; точки А и В, которые не совпадают с данной прямой.
Заданным точкам соответствуют действительные числовые значения xAxA и xBxB.
Координата С — это середина отрезка А и В. Исходя из этого нужно определить значение координаты xCxC .
AB = |a — b|, где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Середина отрезка на плоскости
Зададим следующие параметры: прямоугольная система координат относительно заданной плоскости Oxy; две произвольно расположенные несовпадающие точки, для которых заданы координаты \[\mathrm{A}\left(x_{A} y_{A}\right)\] и \[B\left(\chi_{B} \chi_{B}\right)\]. Точка C — это заданная середина отрезка АВ. Нужно вычислить координаты \[x_{C}\] и \[y_{C}\] относительно точки С.
Чтобы правильно проанализировать задачу, возьмем случай, когда точки A и В между собой не совпадают и расположены на одной координатной плоскости.
В свою очередь координатная плоскость является перпендикулярной относительной одной из осей.
Координаты отметок \[A_{x} A_{y} B_{x} B_{y} C_{x} C_{y}\] — это проекции точек А, В, С.
Рисунок 2. Координатная плоскость с заданным отрезком.Согласно построению, все прямые можно назвать параллельными; прямые также параллельны между собой. Принимая во внимание данное свойство и теорему Фалеса из равенства А С = С В следуют, что все равенства между собой равны. Также они в свою очередь свидетельствуют о том, что точка \[C_{x}\] – это середина отрезка \[A_{x}\] и \[B_{x}\], \[C_{y}\] а – середина отрезка \[A_{y}\] и \[B_{y}\].
Опираясь на полученное выражение получаем основное уравнение середины отрезка на координатной плоскости.
\[x_{c}=\frac{x_{A}+x_{B}}{2}\text { и } y_{c}=\frac{y_{A}+y_{B}}{2}\]
Данным набором формул можно использовать, когда точки А и B лежат на одной координатной плоскости или прямой.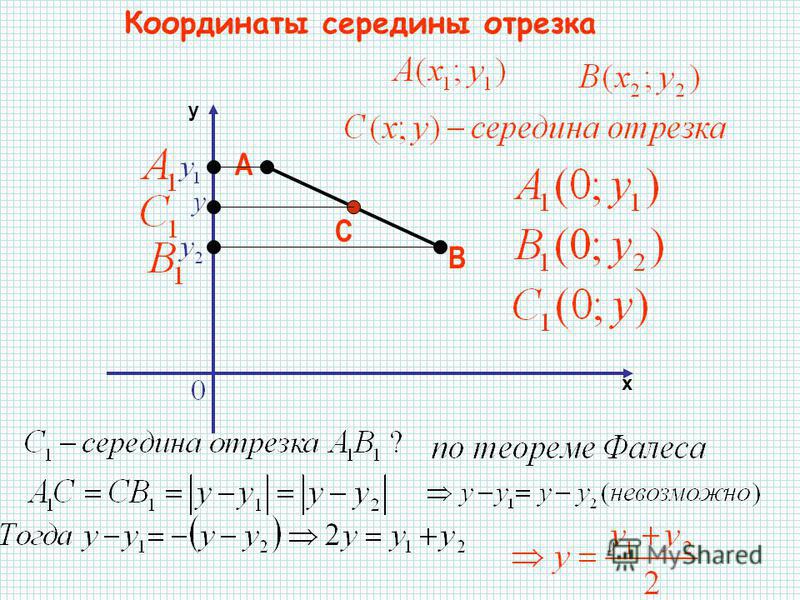
Которая соответственно перпендикулярна относительной одной из осей.
В данном случае координаты отрезка будут определяться по следующей формуле:
\[x_{C}=\frac{x_{A}+x_{B}}{2} \text{ и } y_{c}=\frac{y_{A}+y_{B}}{2}\]
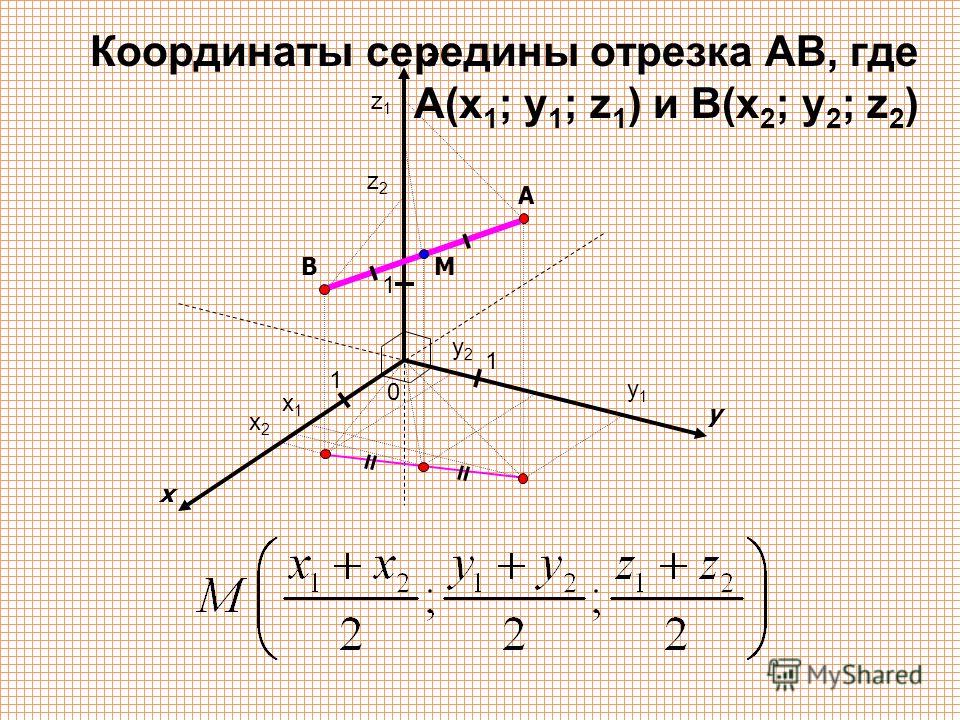
Параметры середины отрезка в пространстве
Для выведения основной формулы для решения подобного рода задач, нужно рассмотреть конкретный пример.
Дана система координат, две произвольные координатные точки с конкретными координатами \[\mathrm{A}\left(A_{x} A_{y} A_{z}\right)\] и \[\mathrm{B}\left(B_{\chi} B_{y} B_{z}\right)\]. Нужно определить отметку точки C, которая в свою очередь будет являться серединой отрезка.
Рисунок 4. Система координат с тремя координатными осями.Согласно основной теоремы Фалеса, все равенства между собой являются равными. Следовательно, значение точек С будут являться серединами отрезков, каждой координатной плоскости, коих имеется три.
Можно составить и записать окончательную формулу для определения середины прямой при координатной плоскости, состоящей более чем двух осей.
\[x_{c}=\frac{x_{A}+x_{B}}{2} \text{ и } y_{C}=\frac{y_{A}+y_{B}}{2}, z_{c}=\frac{z_{A}+z_{B}}{2}\]
Данные формулы также можно применять в случаях, когда точки A и B расположены на одной из координатных прямых. Либо на прямой, которая перпендикулярна относительно одной из осей. Есть еще случай, когда точки расположены в одной координатной плоскости, которая перпендикулярна одной из координатных плоскостей.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для определения отметок середины отрезка, можно определить применяя алгебраическое правило решения векторных выражений.
Исходные данные: прямоугольная декартова система координат Oxy, точки с конкретно заданными координатами \[\mathrm{A}\left(A_{x} A_{y}\right)\] и \[\text { B }\left(B_{x} B_{y}\right)\].
Точка C – это середина отрезка с точками А и В.
Согласно геометрическому правилу и определению, действия над векторами будет выглядеть следующим образом:
\[\overline{O C}=\frac{1}{2} \cdot(\overline{O A}+\overline{O B}).\]
Координата С в данной ситуации — это значение, в которой пересекаются диагонали геометрической фигуры параллелограмм. Данная фигура построена на основании следующих векторов \[\overline{O A}\] и \[\overline{O B}\], иными словами — это точка середины диагоналей.
Координатные показатели радиуса — это векторные показатели, которые равны координатам, тогда будут верны и равенства: \[\overline{O A}\left(x_{A} y_{A}\right)\] и \[\overline{O B}\left(x_{B} y_{B}\right)\].
Выполним следующие действия над векторными значениями и получим следующие формулы:
\[\overline{O C}=\frac{1}{2} \cdot(\overline{O A}+\overline{O B})=\left(\frac{x_{A}+y_{B}}{2}, \frac{y_{A}+y_{B}}{2}\right).\]
Следовательно, заданная координата С обладает данными:
\[\left(\frac{x_{A}+y_{B}}{2}, \frac{y_{A}+y_{B}}{2}\right).
\]
Аналогичным образом определяется нахождение координат середины заданного отрезка в пространстве.
\[C\left(\frac{x_{A}+y_{B}}{2}, \frac{y_{A}+y_{B}}{2}, \frac{z_{A}+z_{B}}{2}\right)\]
Примеры решения задачи, при нахождении точки середины отрезка
Примеры
Пример №1:
Заданы координатные данные. Точка А с показателями (-7,3) и В (2,4).
Нужно определить точку с отметками, которая является серединой отрезка А и В.
Решение:
Середину отрезка можно обозначить любой точкой. В данном примере возьмем наименование точки — С.
Координатные значения ее будут вычисляться как половина суммы координат концов заданного отрезка с точками А
и В.
Составим и запишем следующие формулы:
\[x_{C}=\frac{x_{A}+x_{B}}{2}=\frac{-7+2}{2}=-\frac{5}{2}\\y_{C}=\frac{y_{A}+y_{B}}{2}=\frac{3+4}{2}=\frac{7}{2}\]
Ответ: искомые координатные значения середины отрезка будут равны следующим данным:
\[\mathrm{AB}\left(-\frac{5}{2}, \frac{7}{2}\right)\]
Пример №2:
Заданы координатные отметки геометрической фигуры треугольника: АВС А(-1,0), В (3,2), С (9,-8).
{2}}=\sqrt{58}\]
Ответ: \[\sqrt{58}\].
Видео с вопросом: нахождение координат точек по формуле средней точки
Предположим, 𝐴(−7, −4), 𝐵(6, −9) и 𝐷(8, −2). Если 𝐶 является серединой отрезка 𝐴𝐵 и отрезка 𝐷𝐸, найдите 𝐸.
Стенограмма видео
Предположим, что 𝐴 минус семь, минус четыре; 𝐵 шесть, минус девять; а 𝐷 равно восьми, минус два. Если 𝐶 является серединой обеих линий отрезок 𝐴𝐵 и отрезок 𝐷𝐸, найдите точку 𝐸.
Давайте сначала набросаем то, что мы
знать. У нас есть отрезок 𝐴𝐵 с
середина 𝐶. И 𝐶 также является серединой линии
сегмент 𝐷𝐸. Нам даны координаты 𝐴,
𝐵 и 𝐷. Наша конечная цель – найти
координаты точки 𝐸. Но прежде чем мы сможем найти 𝐸, мы
нужно знать 𝐶. Как только мы найдем 𝐶, мы сможем найти
𝐸.
𝑥-координата средней точки находится путем взятия 𝑥-координат от конечных точек и деления на два. И 𝑦-координата середина находится путем усреднения 𝑦-координат двух конечных точек. Поскольку 𝐶 является серединой 𝐴 и 𝐵, пусть 𝐴 будет 𝑥 один, 𝑦 один и 𝐵 будет 𝑥 два, 𝑦 два. Середина 𝐶 будет расположена в минус семь плюс шесть больше двух, минус четыре плюс минус девять больше двух. Минус семь плюс шесть больше двух равно отрицательная половина. И минус четыре плюс минус девять отрицательно 13. Итак, 𝑦-координата отрицательна 13 больше двух. Теперь мы знаем, где находится 𝐶 расположенный. И мы готовы подумать о 𝐸.
Если 𝐶 также является серединой 𝐷𝐸,
тогда координаты 𝐶 будут равны 𝑥-координатам 𝐷 и 𝐸 усредненным
вместе, а 𝑦-координаты 𝐷 и 𝐸 усреднены вместе.
Нам даны координаты
𝐷. Это восемь, минус два. И так, мы подключаем это. Отсюда мы сделаем два отдельных
уравнения. Мы установим отрицательную половину равной
до восьми плюс 𝑥-координата 𝐸 больше двух. И минус 13 больше двух равно
к отрицательным двум плюс 𝑦-координата 𝐸 больше двух. Мы дадим себе немного
больше места.
Поскольку все знаменатели два, то числители равны между собой. Отрицательная единица равняется восьми плюс 𝑥-координата 𝐸. И решить эту пропажу значение, мы вычитаем восемь с обеих сторон. И мы видим 𝑥-координату для точка 𝐸 минус девять. Чтобы найти 𝑦-координату точка 𝐸, прибавляем по две к обеим сторонам. 𝑦-координата 𝐸 отрицательна 11. В координатной форме точка 𝐸 расположен на отрицательной девятке, отрицательной 11.
Координаты середины прямой АВ (1,2).
Длина АВ 10 единиц.Координатная геометрия
Шайна Б.
спросил 18.02.171. Если градиент AB равен 0, найдите координату AB.
2. Если градиент AB равен 3\4, найти координаты AB.
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Марк М. ответил 18.02.17
Репетитор
4.9 (917)
Репетитор по математике — уровни средней школы/колледжа
Об этом репетиторе ›
Об этом репетиторе ›
1. Поскольку наклон AB равен 0, точки A, B и середина AB имеют одну и ту же координату y, а AB является горизонтальным отрезком.
Поскольку AB имеет длину 10, A и B на 5 единиц левее и правее средней точки.
A = (-4, 2) и B = (6,2)
2. Пусть M=(1,2). Отрезки AM и BM оба имеют длину 5, и, поскольку наклон AB равен 3/4, каждый из них является гипотенузой прямоугольного треугольника с вертикальным катетом 3 и горизонтальным катетом 4.
Чтобы найти A, начните с M, затем переместитесь на 4 единицы влево и на 3 единицы вниз. Чтобы найти B, начните с M, затем переместитесь на 4 единицы вправо и на 3 единицы вверх.
Таким образом, A = (-3, -1) и B = (5, 5)
Голосовать за 0 Понизить
Подробнее
Отчет
Шон В. ответил 18.02.17 92 + 0
10 = x1-x2 или x1 = x2 + 10
Подставим это в (x1+x2) = 2, получим 2×2 + 10 = 2 → x2 = -4 и x1 = 6
Теперь, когда мы нашли Bx (x2) и Ax (x1), нам нужно найти y1 или y2 (помните, что они равны).
Мы можем использовать уравнение (y1+y2) = 4. Поскольку они равны, 2y2 = 4 → y2 = 2 = y1.
Это дает нам A (6, 2) и B (-4, 2).
2. Если градиент равен 3/4, то 4 * (y2-y1) = 3 * (x2-x1). Я использовал дроби и перекрестное умножение, чтобы найти эту связь. Мы можем использовать уравнение расстояния, где я подставляю 3/4 * (x2-x1) в (y2-y1): 92
8 = (x2-x1) → x2 = x1 + 8
Подставьте обратно к (x1+x2) = 2:
2×1 + x2 = -3 и = 5
Теперь мы можем использовать соотношение, которое мы впервые нашли, чтобы найти y2 и y1: -y1) = 24
(y2-y1) = 6
Используя соотношение (y1+y2) = 4:
y2 = 4 — y1
(4 — y1 — y1) = 6
y1 = -1 и y2 = 5
Это дает нам A (-3) и B , 5).
Надеюсь, это поможет!
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
