как найти уравнение касательной
Вы искали как найти уравнение касательной? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как написать уравнение к касательной графику функции, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как найти уравнение касательной».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как найти уравнение касательной,как написать уравнение к касательной графику функции,как написать уравнение касательной к графику функции,как составить уравнение касательной,как составить уравнение касательной к графику,как составить уравнение касательной к графику функции,найти уравнение касательной,найти уравнение касательной к графику функции,найти уравнение касательной онлайн,написать уравнение к касательной к графику функции,написать уравнение касательной,написать уравнение касательной к графику функции,напишите уравнение к касательной к графику функции,напишите уравнение касательной к графику функции,онлайн уравнение касательной к графику функции,составить уравнение касательной,составить уравнение касательной к графику функции,составить уравнение касательной к графику функции онлайн,составить уравнение касательной к графику функции параллельной прямой,составить уравнение касательной к кривой,составьте уравнение к касательной к графику функции,составьте уравнение касательной,составьте уравнение касательной к графику,составьте уравнение касательной к графику функции,составьте уравнение касательной к графику функции f x в точке x0,составьте уравнение касательной к графику функции y,составьте уравнение касательной к графику функции параллельной оси абсцисс,уравнение к касательной к графику функции онлайн,уравнение касательной,уравнение касательной к графику функции,уравнение касательной к графику функции в точке онлайн,уравнение касательной к кривой,уравнение касательной как найти,уравнение касательной как составить,уравнение касательной составить,уравнение касательной формула,уравнения касательной,уравнения касательной к графику функции,формула уравнение касательной,формула уравнения касательной.
Решить задачу как найти уравнение касательной вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Геометрический смысл дифференциала (Лекция №7)
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Пусть имеем функцию y=f(x),
где x – независимая переменная.
Тогда дифференциал этой функции dy=f‘(x)dx также зависит от переменной x,
причем от x зависит только первый
сомножитель f‘(x) , а dx = Δx от x не зависит (приращение в
данной точке x можно выбирать независимо
от этой точки). Рассматривая dy как функцию x, мы можем найти дифференциал этой функции.
Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y: d(dy)=d2y.
Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому
d2y = d(dy) = d[f ‘(x)dx)] = [f ‘(x)dx]’dx = f »(x)dx·dx = f »(x)(dx)2.
Принято записывать (dx)2 = dx2. Итак, d2у= f»(x)dx2.
Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:
d3y=d(d2y)=[f »(x)dx2]’dx=f »'(x)dx3.
Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: dn(y)=d(dn-1y)
| dny = f (n)(x)dxn |
Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:
ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ
Пусть значения двух переменных x и y связаны между собой некоторым уравнением, которое символически запишем так:
F(x, y) = 0.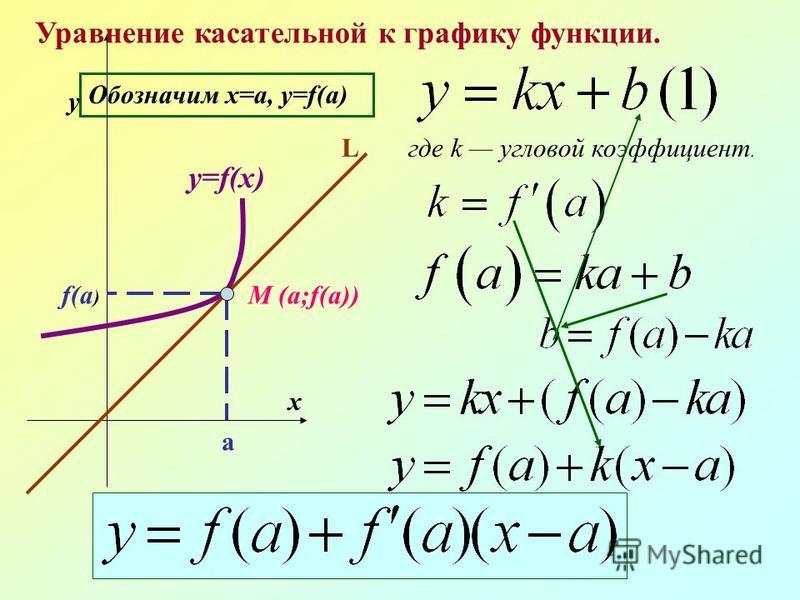
| (1) |
Если на некотором множестве D каждому значению переменной x соответствует единственное значение y, которое вместе с x удовлетворяет уравнению (1), то будем говорить, что это уравнение задает неявную функцию y=f(x).
Из определения следует, что
для любой неявной функции y=f(x), заданной
уравнением (1), имеет место тождество F(x, f(x)) ≡ 0, справедливое при всех
Например, уравнение x2 + y2 – a2 = 0 неявно определяет две элементарные функции . Действительно, после подстановки в исходное уравнение этих значений получим равенство x2+(a2–x2) – a2 = 0.
Однако, не всякую неявно заданную функцию можно представить явно, т.е. в виде y=f(x).
Например, функции, заданные уравнениями y2– y – x2=0 или , не выражаются через элементарные функции, т.
е. эти
уравнения нельзя разрешить относительно y.
Заметим, что каждая явная функция y=f(x) может быть представлена и как неявная y–f(x) = 0.
Таким образом, неявная функция – это определенный способ задания зависимости между переменными x и y.
Рассмотрим правило нахождения производной неявной функции, не преобразовывая ее в явную, т.е. не представляя в виде y=f(x).
Чтобы найти производную у‘ неявной функции F(x, y)=0, нужно обе части этого уравнения продифференцировать по x, рассматривая у как функцию от x, и из этого полученного уравнения найти искомую производную y‘. Чтобы найти y», нужно уравнение F(x, y)=0 дважды продифференцировать по x и выразить y» и т.д.
Примеры. Найти производные функций заданных неявно.
Итак, производная неявной
функции выражается, как правило, не только через аргумент, но и через функцию.
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Пусть даны два уравнения
| x=x(t),y=y(t), где t Î [T1, T2]. | (1) |
Каждому значению t из [T1, T2] соответствуют определенные значения x и y. Если рассматривать значения x и y как координаты точки на плоскости xOy, то каждому значению t будет соответствовать определенная точка плоскости. Когда t изменяется от T1 до T2, эта точка на плоскости описывает некоторую кривую. Уравнения (1) называются параметрическими уравнениями этой кривой, t называется параметром, а способ задания кривой уравнениями (1) называется параметрическим.
Предположим, что функция x=x(t) имеет обратную t=t(x). Тогда, очевидно, у является функцией от x: y=y[t(x)]
.
Следовательно, уравнения (1) определяют y как функцию от x, и
говорят, что функция y от
x задается параметрически.При рассмотрении функций, заданных параметрически, исключение параметра не всегда возможно. Во многих случаях удобнее задавать различные значения t и затем вычислять соответствующие значения аргумента x и функции y.
Пример. Пусть кривая задана параметрическими уравнениями:
Построим эту кривую на плоскости, придавая различные значения параметру t и находя соответствующие значения х и у.
При t =0 M(R, 0).
Таким образом, получаем окружность с центром в начале координат, радиуса R. Здесь t обозначает угол, образованный радиусом, проведенным в некоторую точку окружности М(x, y)
Если исключим из этих
уравнений параметр t,
то получим уравнение окружности, содержащее только x и y.
Возводя в квадрат параметрические уравнения и складывая их, находим:
x2+ y2=R2(cos2t + sin2t) или x2+ y2=R2.
Выведем правило нахождения производных функций, заданных параметрически. Пусть x=x(t), y=y(t), причем на некотором отрезке [T1, T2] функции x(t) и y(t) дифференцируемы и x‘ ≠ 0.
Т.к. у – функция, зависящая от переменной x, то будем считать, что функция x=x(t) имеет обратную t=t(x).
Будем обозначать: yx‘ – производная функции по переменной x, yt‘, xt‘, tx‘ – соответственно производные по t и х.
Воспользовавшись правилом
дифференцирования сложной функции, получим . Производную tx‘ найдем по правилу
дифференцирования обратной функции .
Окончательно, .
Итак,
Полученную функцию можно рассматривать как функцию, заданную параметрически: .
Используя эту формулу, можно находить и производные высших порядков функций, заданных параметрически. Найдем . По определению второй производной . Учитывая, что yx‘ есть функция параметра t, yx‘=f(t), получаем:
Примеры.
- , y = arcsin (t–1). Найдем .
Следовательно, .
- Найти угловой коэффициент касательной к циклоиде x = a·(t – sin t), y = a·(1 – cost)
в произвольной точке (0 ≤t≤ 2·π).
Угловой коэффициент касательной .
x‘ = a·(1 – cost) ,y‘ = a·sin t. Поэтому .
Найти .
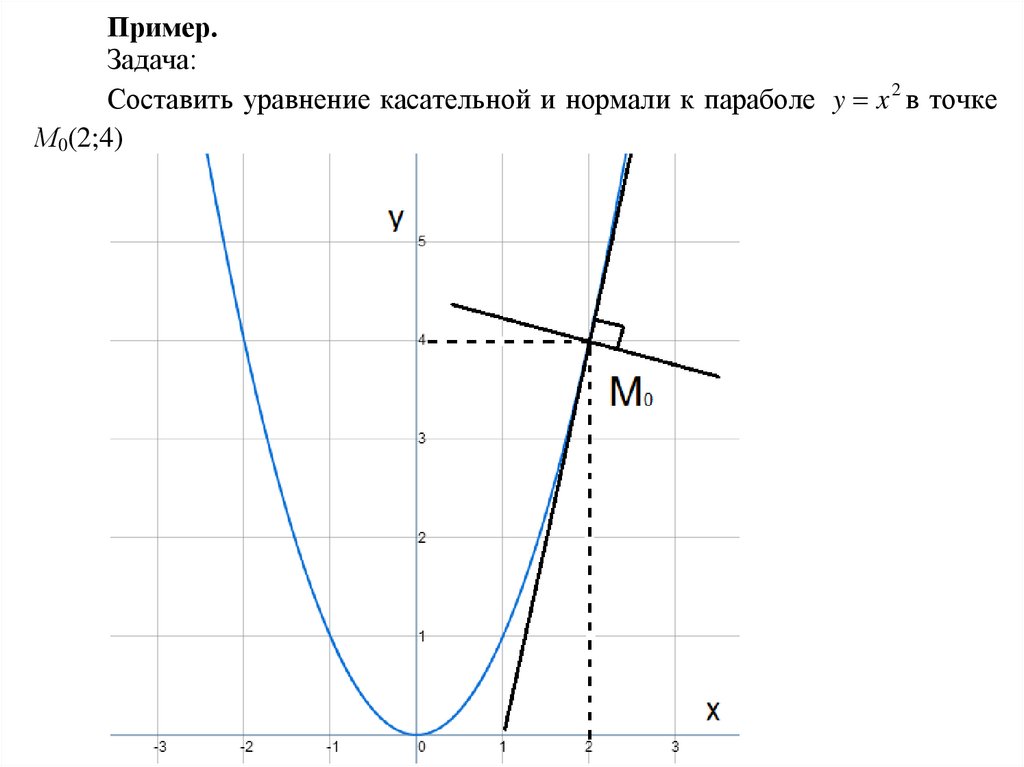
УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ
Рассмотрим кривую, уравнение
которой есть y=f(x).
Возьмем на этой кривой точку M(x0, y0), и составим уравнение
касательной к данной кривой в точке M,
предполагая, что эта касательная не параллельна оси Oy.
Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f‘(x0), то получаем уравнение y= f‘(x0)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x0, y0). Поэтому ее координаты должны удовлетворять уравнению касательной: y0= f‘(x0)·x0 + b. Отсюда b=y0– f‘(x0)·x0.
Таким образом, получаем уравнение касательной y= f‘(x0)·x +y0 – f‘(x0)·x0 или
| y = f ‘(x0)·(x – x0) + f(x0) |
Если касательная, проходящая
через точку М(x0,y0) параллельна оси ординат (т.
е. производная в этой
точке не существует), то ее уравнение x= x0.
Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.
Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.
Из определения нормали следует, что ее угловой коэффициент kn связан с угловым коэффициентом касательной k равенством:
.
Учитывая, что нормаль также как и касательная проходит через точку M(x0, y0), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:
Ясно, что если касательная параллельна
оси Ox, т.е.f‘(x0) = 0 и ее уравнение имеет вид y= y0, то нормаль в этой же точке
будет перпендикулярна оси Ox.
Значит, ее уравнение имеет
вид x= x0.
Примеры.
- Составить
уравнения касательной и нормали к графику функции у = tg2x в точке с абсциссой x0=π/4.
Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4x – π + 1.
Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4·x + π/16 + 1.
- Составить уравнения
касательной и нормали к графику функции у
= 0.5·(x – 2)2 + 5 в точке M(2; 5).
y‘= x – 2, y‘(2) = 0 . Следовательно, касательная параллельна оси Ox, а значит ее уравнение y= 5 . Тогда нормаль параллельна оси Oy и имеет уравнение x= 2 .
- Найти уравнение касательной и нормали к эллипсу в точке M(2; 3).
Найдем y‘ по правилу дифференцирования неявной функции .
Уравнение касательной: ,т.е. .
Уравнение нормали: , т.е. .
- Составить
уравнения касательной и нормали к циклоиде x= t – sin t, y= 1 – cos tв точке М(x0; y0), которая соответствует
значению параметра t = π/2.
При t=π/2x0= π/2 – 1, y0=1.
.
Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2.
Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.
ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Теорема Ролля. Если
функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех
внутренних точках этого отрезка (т.е. на (а;
b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется
хотя бы одна точка c Î (a; b),
в которой f‘(c) = 0.
Доказательство. Так как функция f(x) непрерывна на [a; b], то по одной из теорем о непрерывных функциях она достигает на этом отрезке наибольшего значения и наименьшего. Пусть
Заметим, что если М = m, то f(x) = const = 0 (по условию теоремы f(a)=f(b)=0) и, следовательно, f‘(x)=0при всех x Î [a; b] .
Предположим, что M≠m, тогда, по крайней мере, одно из этих чисел отлично от нуля. Для определенности будем считать, что М ≠0 и М > 0.
Пусть в точке x = c f(c)=М, при этом c≠a и с ≠ b, т.к. f(a)=f(b)=0. Придадим значению c приращение Δx и рассмотрим новую точку c+Δx. Поскольку f(c) – наибольшее значение функции, то f(c+Δx) – f(c)≤0 для любого Δx. Отсюда следует, что
Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная при x = c существует, будем иметь:
Но неравенства f‘(c) ≤ 0 и f‘(c) ≥ 0 одновременно возможны лишь в случае, когда
f‘(c)=0.
Теорема доказана.
Эта теорема имеет простой геометрический смысл. Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ox в точках x=a и x=b, то на этой кривой найдется хотя бы одна точка с абсциссой c, a < c < b, в которой касательная параллельна оси Ox.
Заметим, что доказанная теорема останется справедливой, если предположить, что на концах отрезка функция принимает равные значения f(a)=f(b), не обязательно равные нулю.
Кроме того, отметим, что если внутри [a; b] найдется хотя бы одна точка, в которой производная функции f(x) не существует, то утверждение теоремы может оказаться неверным.
Пример. Функция непрерывна на [–1; 1], обращается в нуль на концах отрезка. Но производная не обращается в нуль ни в одной точке этого отрезка.
Теорема Лагранжа.
Если функция y= f(x)
непрерывна на [a; b] и дифференцируема во всех
внутренних точках этого отрезка, то внутри отрезка [a; b] найдется хотя бы одна
точка c, a<c<b такая, чтоf(b) – f(a)=f‘(c)(b – a).
Доказательство. Обозначим и рассмотрим вспомогательную функцию F(x) = f(x) – f(a) – k(x – a).
Выясним геометрический смысл введенной функции. Для этого рассмотрим график данной функции на [a; b] и напишем уравнение хорды АВ. Заметим, что угловой коэффициент хорды и она проходит через точку A(а; f(a)). Следовательно, ее уравнение
y = f(a) + k(x – a).
Но F(x)=f(x)–[f(a)+k(x–a)]. ПоэтомуF(x) при каждом x есть разность ординат графика y= f(x) и хорды, соответствующих точкам с одинаковой абсциссой.
Легко видеть, что F(x) непрерывна
на [a; b] , как разность непрерывных
функций.
Эта функция дифференцируема внутри [a; b] и F(a)=F(b)=0.
Следовательно, к функции F(x)
можно применить теорему Ролля. Согласно этой теореме
найдется точка c Î (a; b), что F‘(c)=0.
Но F ‘(x) = f‘(x) – k, а значит,F‘(c) = f‘(c) – k = 0.
Подставляя в это равенство значение k, получим
,
что и требовалось доказать.
Теорему Лагранжа
геометрически можно пояснить так. Рассмотрим график функции y=f(x),
удовлетворяющий условиям теоремы и соединим концы графика на [a; b] хордой AB. Как мы уже отметили,
отношение для хорды AB, а f‘(c) есть угловой коэффициент касательной. Следовательно, теорема
утверждает, что на графике функции y=f(x) найдется
хотя бы одна точка, в которой касательная к графику параллельна хорде,
соединяющей концы дуги.
Теорема Коши. Если f(x) и g(x) – две функции, непрерывные на [a; b] и дифференцируемые внутри него, причем g‘(x) ≠ 0 при всех x Î (a; b), то внутри отрезка [a; b] найдется хотя бы одна точка c Î (a; b), что .
Доказательство.Определим число . Заметим, что g(b) – g(a) ≠ 0, т.к. в противном случае выполнялось бы равенство g(b)=g(a) и по теореме Ролля в некоторой точке d Î (a; b)g‘(d) = 0. Это противоречит условию теоремы.
Составим вспомогательную функцию.
F(x) = f(x) – f(a) – k[g(x) – g(a)].
Несложно заметить, что F(a)=F(b)=0. Функция F(x) удовлетворяет на [a;b] всем условиям теоремы Ролля. Следовательно, найдется число сÎ(a; b) такое, что F‘(c) = 0. Но
F'(x) = f'(x) – k·g(x), а значит F‘(c) = f‘(c) – k·g‘(c) = 0,
откуда.
Заметим, что теорему Коши нельзя доказать, применяя теорему Лагранжа к числителю и знаменателю дроби k. Объясните почему.
Уравнение касательной с использованием неявного дифференцирования — Криста Кинг Математика
Три шага для нахождения уравнения касательной с помощью неявного дифференцирования
Использование неявного дифференцирования для нахождения уравнения касательной лишь немного отличается от нахождения уравнения касательной с помощью обычного дифференцирования. Помните, что мы выполняем следующие шаги, чтобы найти уравнение касательной с помощью нормального дифференцирования:0005
Возьмем производную от заданной функции.
Оцените производную в данной точке, чтобы найти наклон касательной.
Подставьте наклон касательной и заданную точку в формулу наклона точки для уравнения прямой ???(y-y_1)=m(x-x_1)???, затем упростите.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.
Этот результат представляет собой уравнение касательной к заданной функции в данной точке. Когда у нас есть функция, которая не определена явно для ???y???, и нахождение производной требует неявного дифференцирования, мы выполняем те же шаги, которые только что описали, за исключением того, что мы используем неявное дифференцирование вместо обычного дифференцирования, чтобы получить производная на шаге 1.
Видеопример использования неявного дифференцирования для получения уравнения касательной прямой 95=10??? в ???(1,2)???
???y-2=\frac{5}{6}(x-1)???
???y-2=\frac{5}{6}x-\frac{5}{6}???
???y=\frac{5}{6}x-\frac{5}{6}+\frac{12}{6}???
???y=\frac{5}{6}x+\frac{7}{6}???
Получите доступ к полному курсу исчисления 1
Начать
Изучите математикуКриста Кинг математика, изучите онлайн, онлайн-курс, онлайн-математика, неявное дифференцирование, уравнение касательной линии, уравнение касательной линии, касательная точка, точка касания, производные, дифференцирование, неявное дифференцирование, касательная линия, касательная линия уравнение
0 лайковКак найти уравнение касательной – mathsathome.com
Как найти уравнение касательной: видеоурок
Что такое касательная к кривой?
Касательная к кривой — это прямая линия, которая касается кривой только в одной точке. Касательная линия имеет тот же градиент, что и кривая в этой точке.
Касательная к приведенной выше кривой показана красным цветом.
Касательная к кривой просто касается кривой в заданной точке. Он не проходит через кривую в этой точке, хотя может пересекать кривую в другом месте.
Линия, проходящая через две точки кривой, называется секущей. Секущая линия показана зеленым цветом выше. Это не касательная линия.
Как найти уравнение касательной с помощью дифференцирования
Пример 1: Уравнение касательной к параболе
Например, найдите уравнение касательной к кривой в точке (1, 3).
Шаг 1. Дифференцировать функцию кривой
Если , то
Шаг 2. Подставить координату x заданной точки в эту производную, чтобы найти градиент ‘m’
Градиент в любом месте кривой определяется функцией градиента .
Касательная находится в точке (1, 3).
Здесь х=1.
Подставляя x=1 в функцию градиента, можно найти градиент в этой точке.
и так, m=5.
Шаг 3. Подставьте данные координаты (x,y) вместе с ‘m’ в ‘y=mx+c’ и затем решите, чтобы найти ‘c’
Поскольку касательная находится в точке (1, 3 ), здесь x = 1 и y = 3.
Ранее было установлено, что значение m в этой точке равно m = 5.
Касательная представляет собой прямую линию, поэтому она представлена уравнением прямой линии .
Подставляя в это уравнение значения x = 1, y = 3 и m = 5, получаем .
Решая это уравнение относительно с, находим, что с = -2.
Шаг 4. Подставить эти значения m и c в y=mx+c
Было обнаружено, что m = 5 и c = -2.
Заменив эти значения в , уравнение касательной будет .
Как найти, где касательная снова встречается с кривой
Чтобы найти, где касательная снова встречается с кривой, сначала найдите уравнение касательной.
Затем используйте одновременные уравнения, чтобы решить как уравнение касательной, так и уравнение кривой. Каждая пара решений x и y соответствует координате (x, y), где касательная пересекает кривую.
Например, найдите касательную к точке (-1, 2) и найдите координаты, в которых касательная снова пересекает кривую.
Во-первых, уравнение касательной находится.
Так как производная .
Подставляя в эту производную, находим, что .
Подставляя , и в ,
и т.д., .
Следовательно, так как и уравнение касательной .
Чтобы найти, где касательная к кривой снова встречается с кривой, одновременно решите уравнение касательной и уравнение кривой.
Синхронные уравнения используются для нахождения координат пересечения двух линий.
Уравнения и можно решить, установив уравнения равными друг другу, чтобы получить .
Умножая каждый член на , уравнение принимает вид .
Вычитаем по 2 с обеих сторон, чтобы уравнение стало равным нулю: .
Разделив каждый член на 2, получим уравнение: .
Мы уже знаем, что найдено одно решение при , поэтому один фактор должен быть .
Деление с использованием полиномиального длинного деления дает результат , который разлагается на .
Поэтому можно записать как .
Следовательно, либо (что приводит к исходному решению , либо , что дает нам новое решение .
Когда , координата y может быть найдена путем подстановки ее обратно в, чтобы получить .
Следовательно, касательная снова пересекает кривую at
Формула уравнения касательной
Уравнение касательной к y=f(x) в точке x=a задается формулой: y=f'(a)(x-a)+f (а)
Формула уравнения касательной получена из .
Градиент касательной при равен производной в точке , которая определяется выражением.
и можно взять любую и точки на касательной.
равно и равно .
Уравнение градиента становится таким, которое можно изменить, чтобы получить .
Уравнение касательной к в точке находится по формуле: .
Например, найти уравнение касательной в точке (0, 0).
Координата x точки (0, 0) равна 0, поэтому a = 0.
Дифференцируя функцию, .
находится подстановкой x = 0 в .
Поэтому и так .
находится подстановкой x = 0 в .
Поэтому и так .
Чтобы найти уравнение касательной, подставьте , и в .
Это упрощается до .
Уравнение касательной к окружности
Чтобы найти уравнение касательной к окружности:
Например, найдите касательную к окружности в точке (0, 5).
Шаг 1. Найдите градиент от центра окружности до точки касания
Центр круга находится в (1, 3).
Точка касания находится в точке (0, 5).
Градиент находится с помощью .
Оценивая это по двум точкам, что равно -2. Градиент между центром и заданной точкой равен -2.
Шаг 2. Вычислите отрицательную обратную величину этого градиента, чтобы найти «m»
Градиент касательной к окружности перпендикулярен градиенту от центра к той же точке.
Градиент линии определяется обратной отрицательной величиной градиента линии, перпендикулярной к ней.
Чтобы вычислить отрицательное обратное число, вычислите -1, деленное на это число.
, поэтому градиент касательной к окружности в этой точке равен .
Значение m для касательной к окружности равно .
Шаг 3. Подставьте значения координат x и y вместе с ‘m’ в ‘y=mx+c’ и найдите c
Касательная находится в точке (0, 5), поэтому мы подставляем , и m = в уравнение прямой.
В результате получается .
Шаг 4. Подставить значения ‘m’ и ‘c’ обратно в ‘y=mx+c’
Было найдено, что m = и c = 5.
Следовательно, уравнение касательной к окружности имеет вид
Уравнение касательной к функции квадратного корня
Тангенс функции квадратного корня можно найти, продифференцировав его и подставив координату x, чтобы найти градиент. Это можно сделать, написав функцию внутри квадратного корня в степени, равной половине. Затем это можно дифференцировать с помощью цепного правила.
Например, найти уравнение касательной к функции в точке (6, 2).
Мы можем использовать формулу уравнения касательной: .
Шаг 1. Дифференцируем функцию
, и это можно записать как .
Это можно отличить, используя цепное правило, чтобы получить .
Шаг 2. Найдите f'(a) и f(a)
‘ a’ — координата x точки, в которой касательная пересекает кривую. В этом примере .
находится путем подстановки значения « a» в уравнение.
и так далее, .
находится путем подстановки значения «a» в уравнение.
и так далее, .
Шаг 3. Подставляем значения f(a), f'(a) и a в формулу тангенса
и таким образом уравнение тангенса принимает вид .
Это упрощается до .
Умножая каждый член на 4, это также можно записать как или переставить как .
Уравнение касательной к y=sin(x)
Найдите уравнение касательной к в точке .
Шаг 1. Продифференцируем функцию
и .
Шаг 2. Найдите f'(a) и f(a)
‘a’ — координата x точки, в которой касательная пересекает кривую. В этом примере .
находится подстановкой в .
и так далее, .
находится подстановкой в .
и так далее, .
Шаг 3. Подставить значения f(a), f'(a) и a в формулу тангенса
и, таким образом, уравнение тангенса примет вид .
Это расширяется, чтобы дать .
Умножая каждый член на 8, получаем: .
Факторизация , это становится .
Деление на 8 с обеих сторон, .
Уравнение касательной с неявным дифференцированием
Чтобы найти уравнение касательной с помощью неявного дифференцирования:
Например, найдите уравнение касательной к в точке (3, 2).
Шаг 1. Неявное дифференцирование функции
При неявном дифференцировании дифференцируйте каждый член, как обычно, но не забывайте ставить после каждого члена y.
неявно отличается от .
Шаг 2. Оцените производную, используя значения координат x и y, чтобы найти «m»
В точке (3, 2) и .
Подставляя их в , получаем .
Следовательно, переставляя , получаем .
Это значение m в нашем уравнении прямой линии.
Шаг 3. Подставьте координаты x и y вместе с этим значением m в (y-y1)=m(x-x1)
Уравнение прямой может быть задано как .
и .
Поэтому уравнение становится .
Можно расширить, чтобы получить .
Прибавляя 2 к обеим сторонам и упрощая, . Это можно записать как .
Как найти уравнение касательной из внешней точки
Чтобы найти касательную к кривой из внешней точки, сначала найдите точку «а» на кривой, где проходит касательная. Для этого продифференцируем функцию и приравняем ее к изменению у по сравнению с изменением х от внешней точки до точки «а» на кривой. Решите это для «а». Как только положение «а» найдено, найдите уравнение касательной обычным способом.
Например, найдите уравнение касательных к кривой, проходящей через точку (1, 1).
Из этой точки к кривой можно пройти двумя касательными.
Места, в которых касательная пересекает кривую, будут иметь координату x и координату y .
Шаг 1. Продифференцировать функцию
Если , то .
Шаг 2. Установить производную в точке a равной градиенту между внешней точкой и кривой
В точке пересечения касательной с кривой и т. д. .
Градиент между двумя точками равен .
будет взято за точку на кривой.
будет считаться внешней точкой.
Поэтому становится . Это упрощает до .
Значение касательной должно быть равно этому градиенту.
Поэтому .
Шаг 3. Решите это уравнение, чтобы найти положение касательной в точке «а»
Умножив на a-1, приведенное выше уравнение станет
Раскрывающие скобки: .
Так как это квадратичное число, мы преобразуем правую часть уравнения, чтобы сделать его равным нулю: .
Факторинг: и так, или .
Следовательно, касательная пересекает кривую в точке или .
Подставьте эти значения обратно, чтобы получить (0, 2) и (2, 4) соответственно.