Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .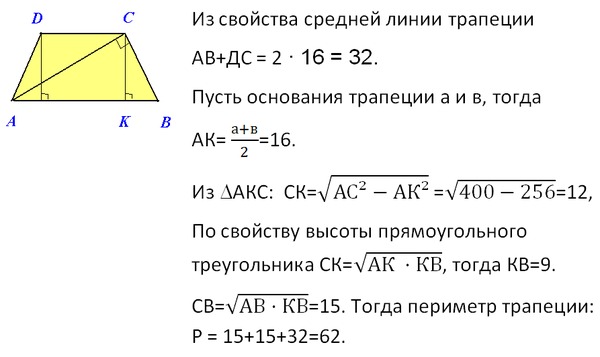
Решено
На полке было 12 книг. Несколько книг взяли с полки. После этого осталось на 4 книги больше, чем взяли. Сколько книг взяли с полки?
как решить задачу 1,3,5,7,9,11,13,15 используя 3 числа чтоб ответ получился 30 одно и тоже число можно использовать несколько раз несколько раз
Схема района, где живут Маша и Саша, выполнена в масштабе 1:1000. Начертите маршруты, по которым они могут ходить в школу друг к другу в гости и из…
Стоимость автомобиля с гаражом составляет…
Пользуйтесь нашим приложением
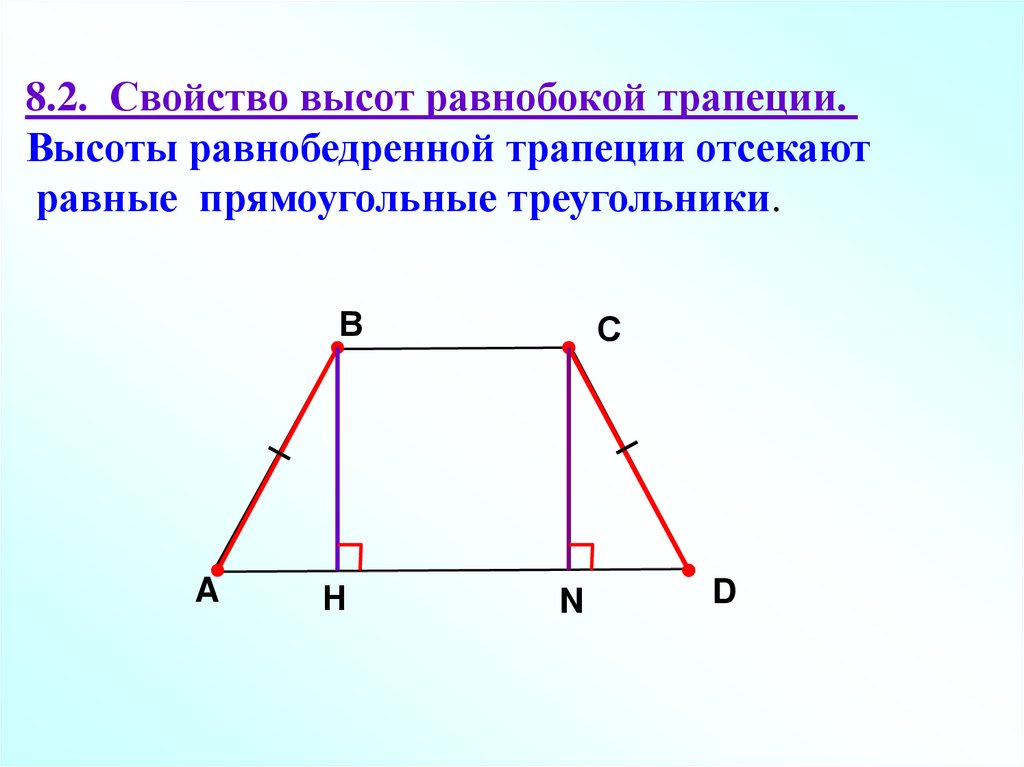
614 диагонали прямоугольной трапеции. Диагонали трапеции. Свойства отрезка, параллельного основаниям трапеции
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.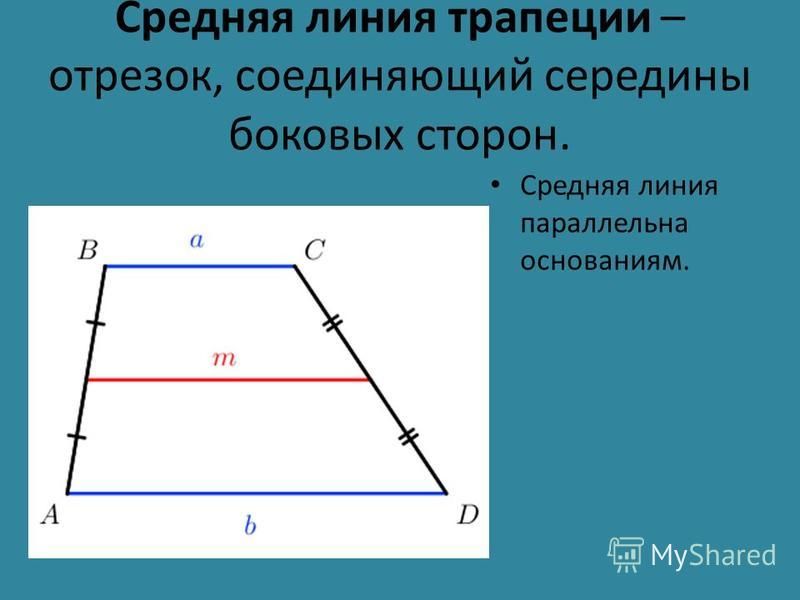
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥ DF как основания трапеции, BD∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3.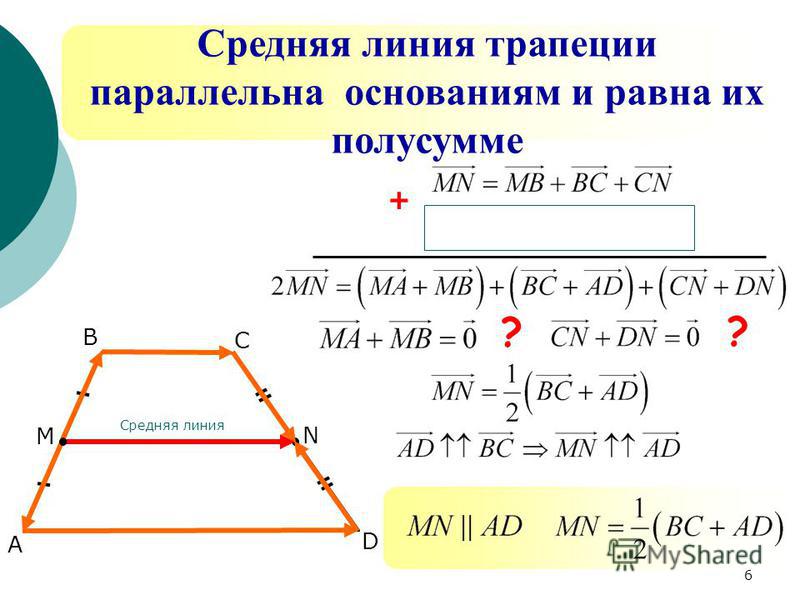 Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.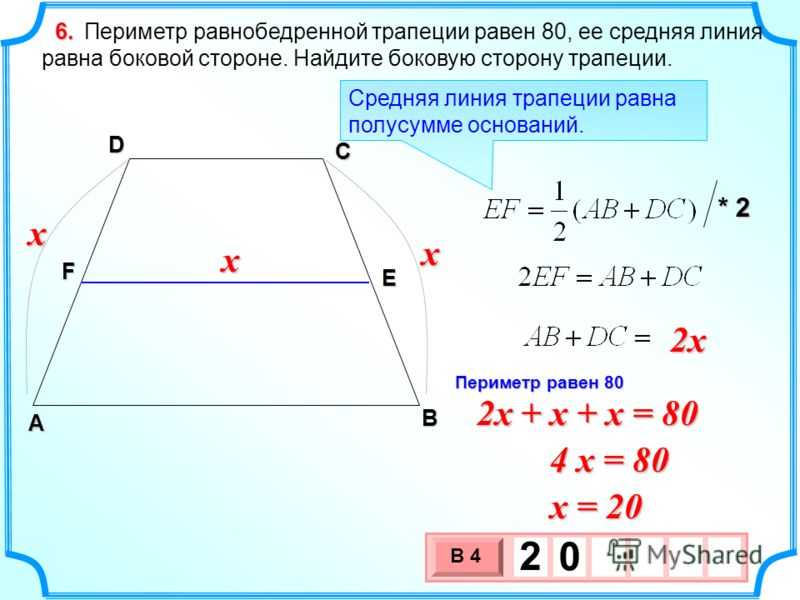
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание . В данном уроке приведено решение задач по геометрии о трапециях.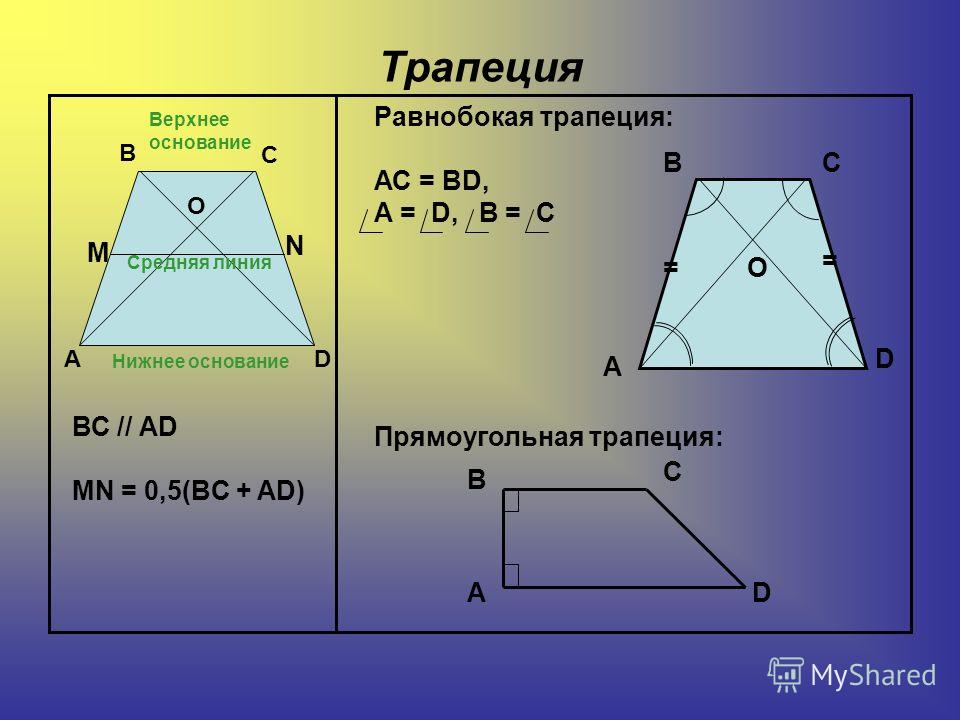 Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме .
Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме .
Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .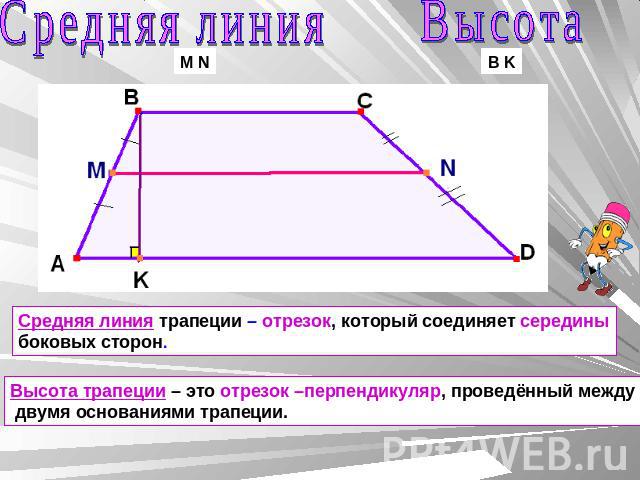
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
Как найти площадь трапеции если. Как найти площадь равнобедренной трапеции
А . Теперь можно приступить к рассмотрению вопроса, как найти площадь трапеции. Эта задача в быту встречается очень редко, но иногда возникает необходимость, например, найти площадь комнаты в форме трапеции, которая все чаще используется при строительстве современных квартир, или в дизайнерских проектах реконструкции.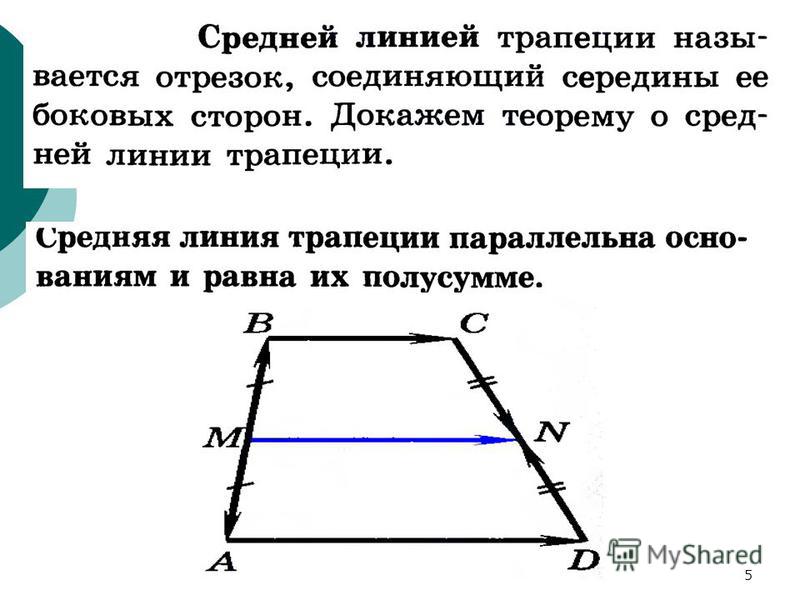
Трапеция – геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны друг другу и называются основаниями трапеции. Два других сегмента называются сторонами трапеции. Кроме того, в дальнейшем нам понадобится еще одно определение. Это средняя линия трапеции, представляющая собой отрезок, соединяющий середины сторон и высоту трапеции, равную расстоянию между основаниями.
Как и треугольники, трапеция имеет отдельные виды в виде равнобедренной (равнобедренной) трапеции, у которой длины сторон одинаковы, и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна половине суммы оснований и параллельна им.
- Равнобедренные трапеции имеют равные стороны и углы, которые они образуют с основаниями.
- Середины диагоналей трапеции и точка пересечения ее диагоналей лежат на одной прямой.

- Если сумма сторон трапеции равна сумме оснований, то в нее можно вписать окружность
- Если сумма углов, образованных сторонами трапеции при любом ее основании равно 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. Наоборот. Если в окружность вписана трапеция, то она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции, будет перпендикулярен ее основаниям и представляет собой ось симметрии.
Как найти площадь трапеции .
Площадь трапеции будет равна половине суммы ее оснований, умноженной на ее высоту. В виде формулы это записывается как выражение:
где S — площадь трапеции, a,b — длина каждого из оснований трапеции, h — высота трапеции.
Вы можете понять и запомнить эту формулу следующим образом. Как следует из рисунка ниже, трапецию с помощью средней линии можно преобразовать в прямоугольник, длина которого будет равна половине суммы оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один-два треугольника, а если вам так проще, то найти площадь трапеции как сумму площадей составляющих ее фигур .
Есть еще одна простая формула для расчета его площади. Согласно ему площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается как: S = m * h, где S — площадь, m — длина средней линии, h — высота трапеции. Эта формула больше подходит для математических задач, чем для бытовых, так как в реальных условиях вы не узнаете длину средней линии без предварительных расчетов. И вы будете знать только длины оснований и сторон.
В этом случае площадь трапеции можно найти по формуле:
S = ((a + b) / 2) * √c 2 — ((b-a) 2 + c 2 -d 2 / 2 (b-a)) 2
где S – площадь, a,b – основания, c,d – стороны трапеции.
Есть еще несколько способов найти площадь трапеции. Но, они примерно так же неудобны, как и последняя формула, а значит, нет смысла на них останавливаться. Поэтому рекомендуем использовать первую формулу из статьи и желаем всегда получать точные результаты.
Поэтому рекомендуем использовать первую формулу из статьи и желаем всегда получать точные результаты.
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие — нет. Параллельные противоположные стороны называются основаниями, а две другие – сторонами трапеции. Отрезок, соединяющий середины сторон, называется средней линией. Трапеции бывают нескольких видов: равнобедренные, прямоугольные, криволинейные. Для каждого типа трапеций существуют формулы нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание равно a, нижнее — b, а высота — h. Тогда можно вычислить площадь S по формуле:
S = ½ * (a + b) * h
т.е. возьмите половину суммы оснований, умноженных на высоту.
Вы также можете вычислить площадь трапеции, если знаете значение высоты и средней линии.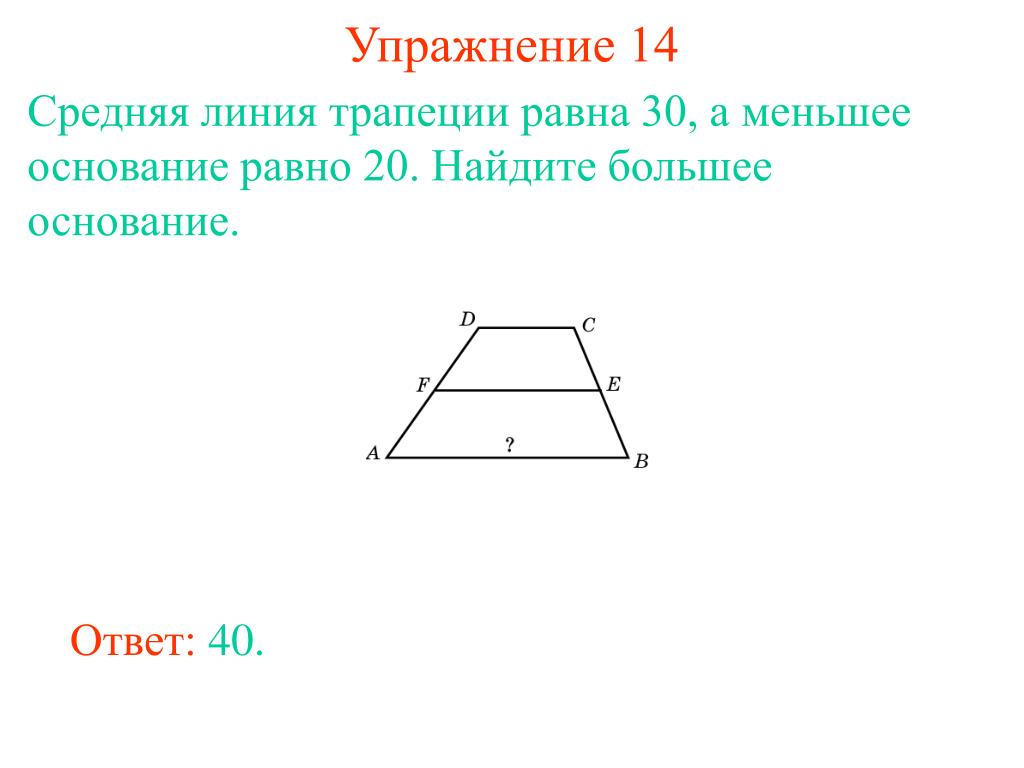 Обозначим среднюю линию — m. Затем
Обозначим среднюю линию — m. Затем
Решим задачу посложнее: нам известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь находится по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sinα
где d с индексы 1 и 2 — диагонали. В этой формуле при расчете дается синус угла.
При известных длинах основания a и b и двух углах у нижнего основания площадь рассчитывается следующим образом:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция является частным случаем трапеции. Отличие ее в том, что такая трапеция представляет собой выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Его стороны равны.
Есть несколько способов найти площадь равнобедренной трапеции.
- По трем сторонам. В этом случае длины сторон будут совпадать, поэтому они обозначаются одним значением — с, а и b — длины оснований:
- Если известны длина верхнего основания, боковой стороны и угол при нижнем основании, то площадь рассчитывается следующим образом:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — сторона.
- Если вместо верхнего основания известна длина нижнего основания — b, то площадь рассчитывается по формуле:
S = c * sin α * (b — c * cos α)
- Если известны два основания и угол при нижнем основании, площадь вычисляется по тангенсу угла:
S = ½ * (b2 — a2) * tg α
- Также площадь вычисляется через диагонали и угол между ними. При этом диагонали равны по длине, поэтому каждая обозначается буквой d без индексов:
S = ½ * d2 * sinα
- Вычислите площадь трапеции, зная длину боковой стороны, среднюю линию и угол при нижнем основании.
Пусть сторона — с, средняя линия — м, угол — а, тогда:
S = m * c * sinα
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее сторон. Затем площадь находится через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sinα
Такой же расчет производится через диаметр D вписанной окружности (кстати, он совпадает с высота трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется следующим образом:
S = a*b/sinα
(эта и последующие формулы справедливы только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется следующим образом:
Если известны только основания, то площадь вычисляется по формуле:
Через основания и боковую линию, площадь трапеции с вписанной окружностью и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из сторон перпендикулярна основаниям. В этом случае длина стороны совпадает с высотой трапеции.
Прямоугольная трапеция состоит из квадрата и треугольника. Найдя площадь каждой из фигур, сложите результаты и получите общую площадь фигуры.
Также общие формулы расчета площади трапеции подходят для расчета площади прямоугольной трапеции.
- Если длины оснований и высота (или перпендикулярная сторона) известны, то площадь рассчитывается по формуле:
S = (a + b) * h / 2
Поскольку h (высота) может быть сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ вычисления площади — умножить длину средней линии на высоту:
или по длине боковой перпендикулярной стороны:
- Следующий метод расчета — через половину произведения диагоналей на синус угла между ними:
S = ½ * d1 * d2 * sinα
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если взять длины сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция – плоская фигура, ограниченная графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , оси x и прямых линиях x = а, х = б. На самом деле две его стороны параллельны друг другу (основаниям), третья сторона перпендикулярна основаниям, а четвертая представляет собой кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищется через интеграл по формуле Ньютона-Лейбница:
Как вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают такими же свойствами углов. Как и у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к стороне, равна 180 градусов.
А сумма углов, прилежащих к стороне, равна 180 градусов.
Площадь трапеции. Привет! В данной публикации мы рассмотрим эту формулу. Почему это так и как вы можете это понять? Если есть понимание, то учиться ему не нужно. Если просто хотите посмотреть эту формулу и что срочно, то можете сразу листать страницу вниз))
Теперь подробно и по порядку.
Трапеция — четырехугольник, две стороны которого параллельны, а две другие — нет. Те, которые не параллельны, являются основаниями трапеций. Два других называются сторонами.
Если стороны равны, то трапеция называется равнобедренной. Если одна из сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапеция изображается так — большее основание внизу, соответственно меньшее вверху. Но никто не запрещает изображать его и наоборот. Вот эскизы:
Следующее важное понятие.
Срединная линия трапеции — это отрезок, соединяющий середины сторон.
Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте углубимся. Почему именно?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и проведем дополнительные построения: через основания проведем прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
* Буквенные обозначения вершин и других точек намеренно не вводятся во избежание ненужных обозначений.
Смотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 равны. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезки, то у нас получится отрезок (это сторона прямоугольника), равный средней линии. Далее, если «приклеить» отрезанные синий и красный отрезки к верхнему основанию трапеции, то у нас тоже получится отрезок (это тоже сторона прямоугольника), равный средней линии трапеции.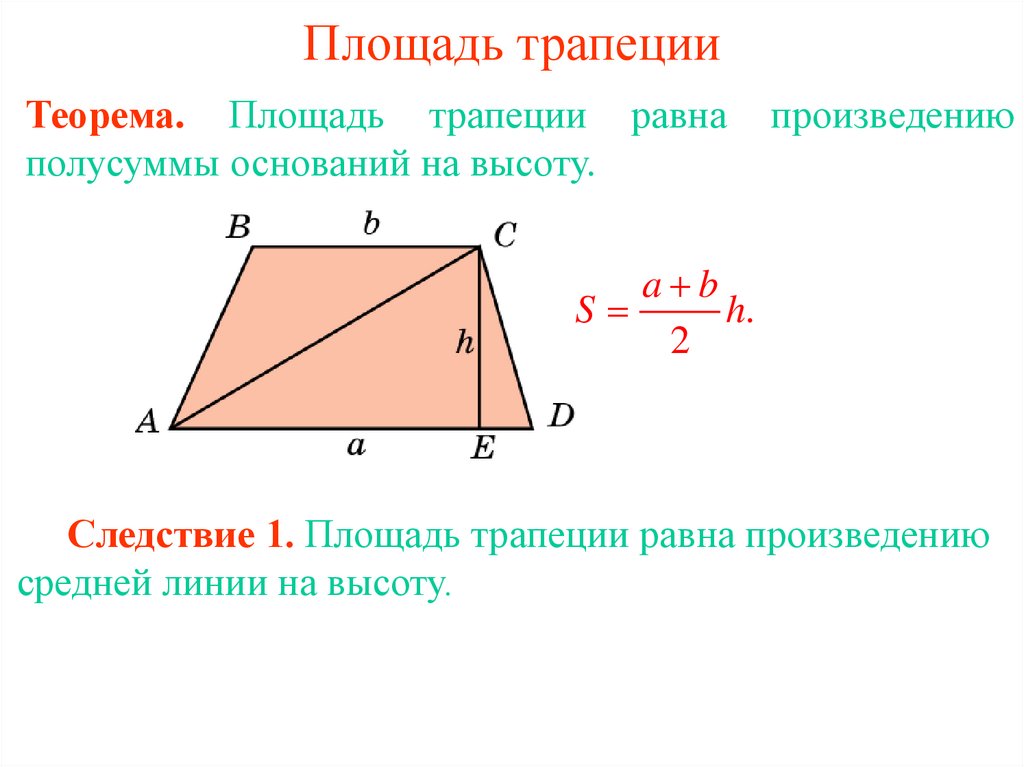
Понятно? Получается, что сумма оснований будет равна двум медианам трапеции:
См. другое объяснение
Сделаем следующее — построим прямую, проходящую через нижнее основание трапеции и прямая, которая пройдет через точки А и В:
Получаем треугольники 1 и 2, они равны по стороне и прилежащим углам (второй признак равенства треугольников). Это означает, что полученный отрезок (на эскизе он отмечен синим цветом) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия этой трапеции и средняя линия треугольника совпадают.
Известно, что треугольник равен половине параллельного ему основания, то есть:
Ладно, понял. Теперь о площади трапеции.
Формула площади трапеции:
Говорят: площадь трапеции равна произведению половины суммы ее оснований и высоты.
То есть получается, что он равен произведению средней линии на высоту:
Вы наверное уже заметили, что это очевидно.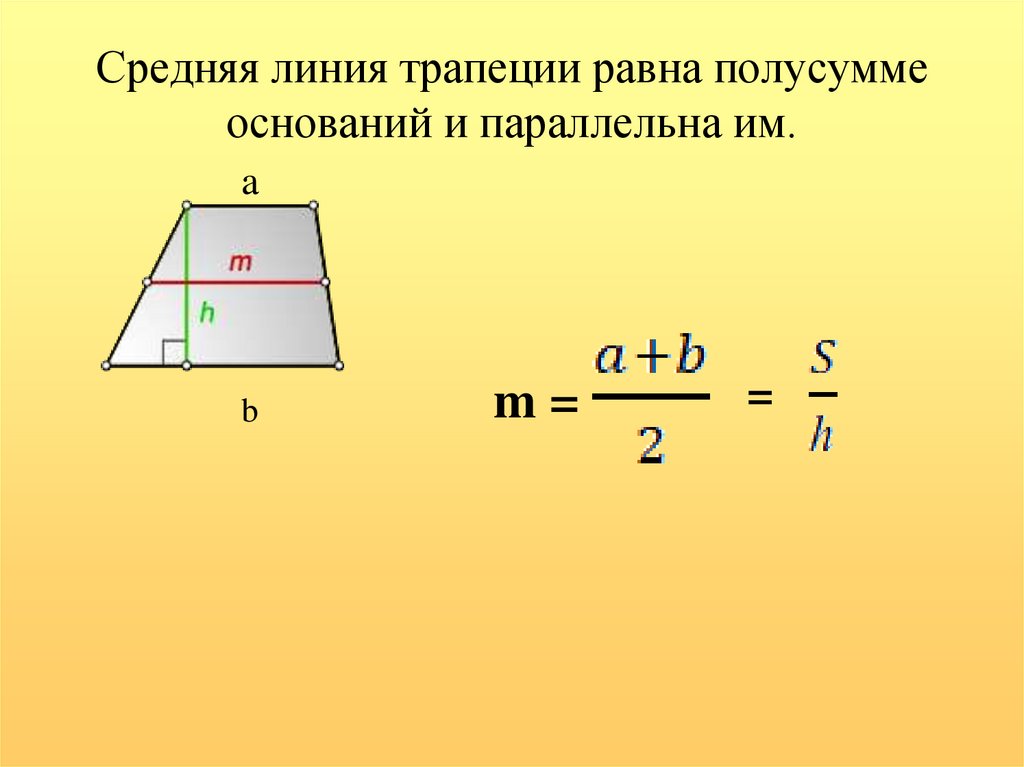 Геометрически это можно выразить так: если мысленно отрезать от трапеции треугольники 2 и 4 и положить их на треугольники 1 и 3 соответственно:
Геометрически это можно выразить так: если мысленно отрезать от трапеции треугольники 2 и 4 и положить их на треугольники 1 и 3 соответственно:
Тогда получится прямоугольник, площадь которого равна площади наша трапеция. Площадь этого прямоугольника будет равна произведению средней линии на высоту, то есть мы можем написать:
Но тут дело не в написании, конечно, а в понимании.
Скачать (просмотреть) материал статьи в формате *pdf
Вот и все. Удачи тебе!
С уважением, Александр.
Раздел содержит задачи по геометрии (планиметрия сечений) о трапециях. Если вы не нашли решение проблемы — напишите об этом на форуме. Курс обязательно будет обновляться.
Трапеция. Определение, формулы и свойства
Трапеция (от др.-греч. τραπέζιον — «стол»; τράπεζα — «стол, еда») — четырехугольник, у которого ровно одна пара противоположных сторон параллельна.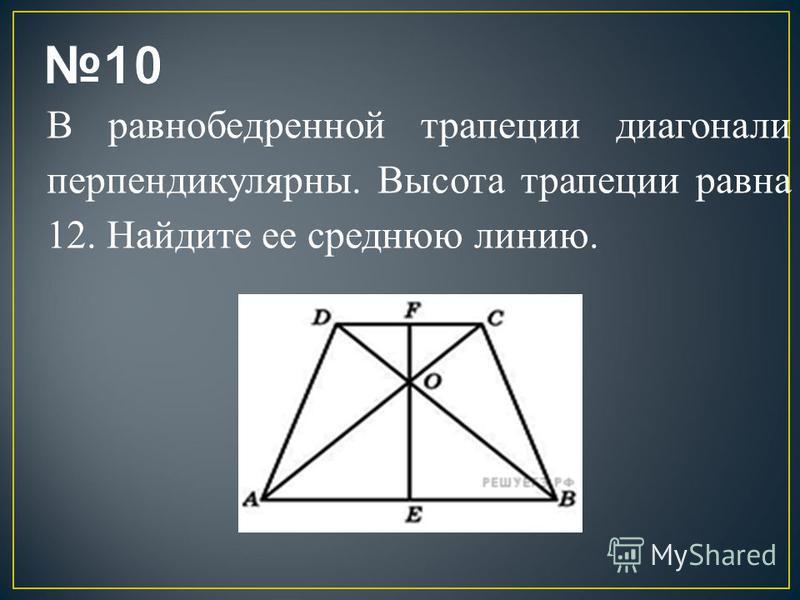
Трапеция – это четырехугольник, у которого две противоположные стороны параллельны.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие – сторонами.
Трапеции бывают:
— универсальные ;
— равнобедренный ;
— прямоугольный
.
красных и коричневых цветов обозначены боковые стороны, зеленый и синий — основания трапеций.
А — равнобедренная (равнобедренная, равнобедренная) трапеция
Б — прямоугольная трапеция
С — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
Стороны равны, а основания параллельны.
Основания параллельны, одна сторона перпендикулярна основаниям, а вторая сторона наклонена к основаниям.
Свойства трапеции
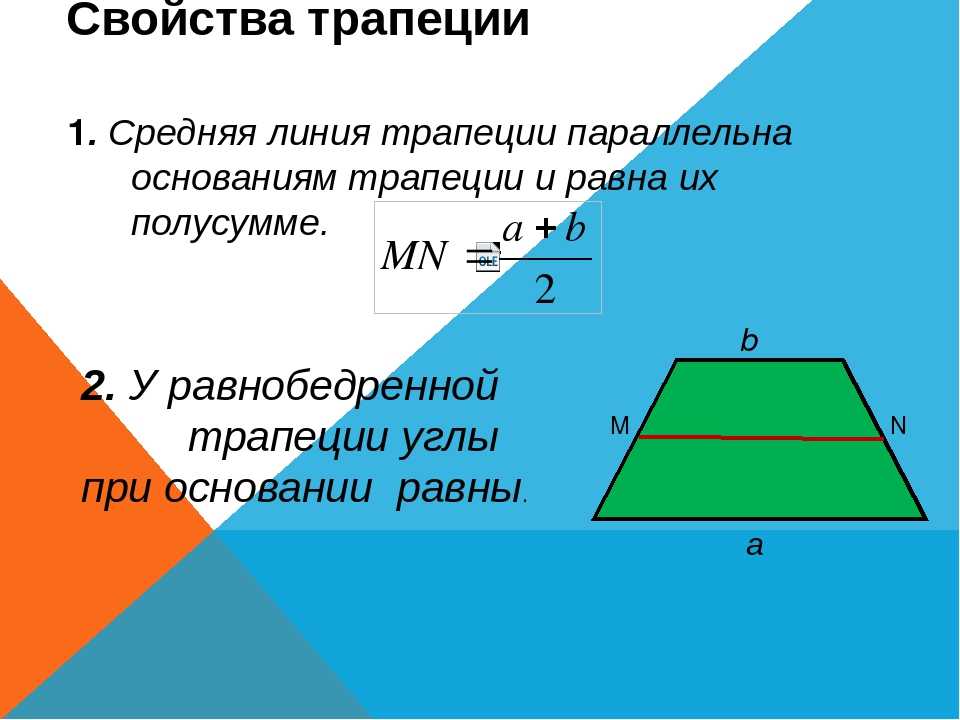
- Срединная линия трапеции параллельна основаниям и равна половине их суммы
- Отрезок, соединяющий середины диагоналей , равен половине разности оснований и лежит на средней линии.
 Его длина
Его длина - Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают пропорциональные отрезки от сторон угла (см. теорему Фалеса)
- Точка пересечения диагоналей трапеции , точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники на основаниях Трапеции, вершины которых являются точками пересечения их диагоналей, подобны. Отношение площадей таких треугольников равно квадрату отношения оснований трапеции
- Треугольники со сторонами трапеции, вершины которых являются точкой пересечения ее диагоналей, равны по площади (равны по площади)
- в трапецию можно вписать окружность , если сумма длин оснований трапеции равна сумме длин ее сторон. Срединная линия в этом случае равна сумме сторон, деленной на 2 (поскольку срединная линия трапеции равна половине суммы оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последним пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab/(a+b) (формула Буракова)
Уголки трапециевидные
Уголки трапеции острые, прямые и тупые .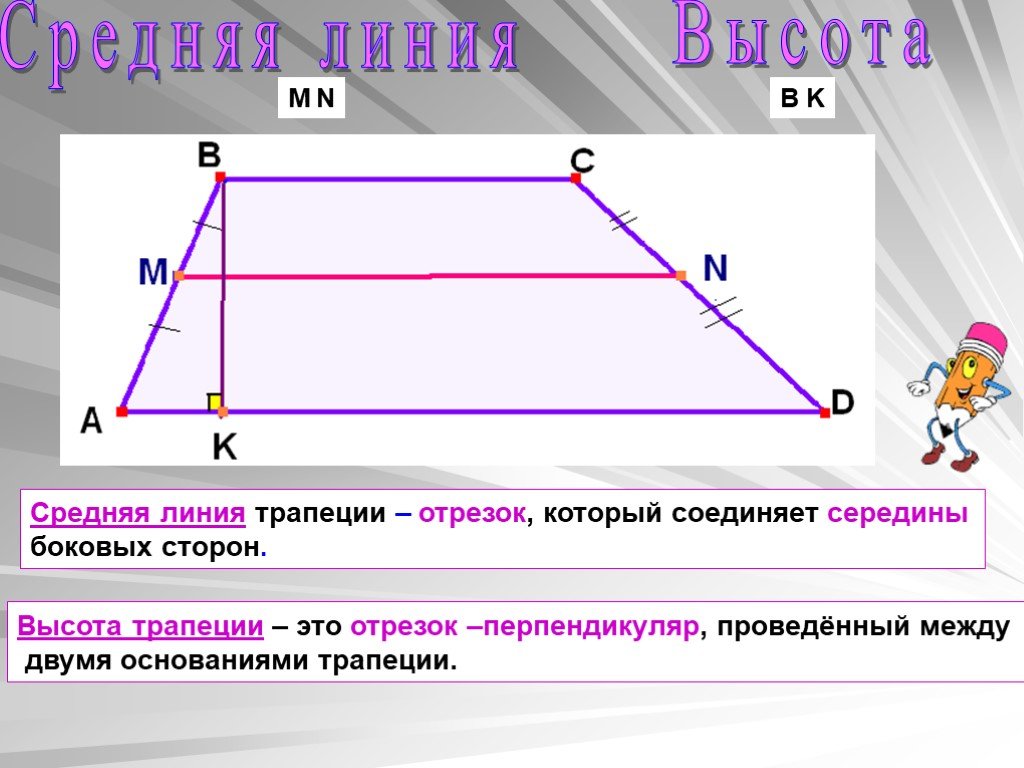
Прямых углов всего два.
Прямоугольная трапеция имеет два прямых угла , а два других — острые и тупые. Другие виды трапеций имеют: два острых угла и два тупых.
Тупые углы трапеции относятся к наименьшим по длине основания, а острые — больше основания.
Любую трапецию можно рассматривать как усеченный треугольник , линия сечения которого параллельна основанию треугольника.
Важно . Обратите внимание, что таким образом (достраиванием трапеции к треугольнику) можно решить некоторые задачи о трапеции и доказать некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции производится по формулам, которые приведены ниже:
В этих формулах используются обозначения, как на рисунке.
а — наименьшее из оснований трапеции
b — наибольшее из оснований трапеции
c,d — стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеция равна удвоенному произведению оснований трапеции на сумму квадратов сторон (формула 2)
Трапеция называется четырехугольником только две стороны параллельны друг другу.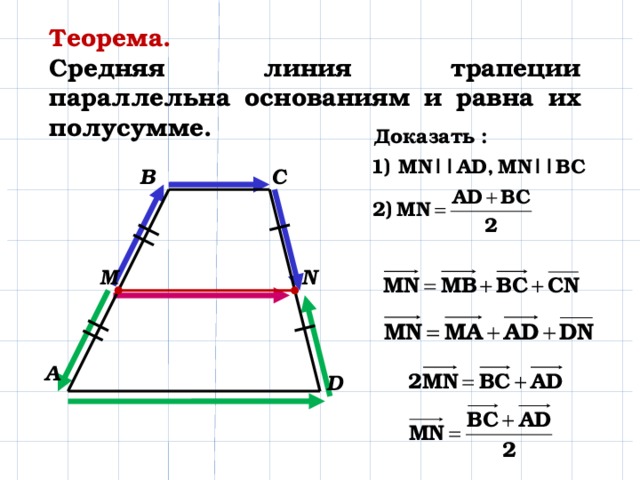
Они называются основаниями фигуры, остальные — сторонами. Параллелограмм считается частным случаем фигуры. Существует также криволинейная трапеция, которая включает в себя график функции. В формулы площади трапеции входят почти все ее элементы, и в зависимости от заданных значений выбирается наилучшее решение.
Главные роли в трапеции отведены высоте и средней линии. средняя линия — это линия, соединяющая середины сторон. Высота Трапеция проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равна произведению половины суммы длин оснований, умноженной на высоту:
Если по условию известна средняя линия, то эта формула сильно упрощается, так как равна половине суммы длин оснований:
Если по условию даны длины всех сторон, то можно рассмотреть пример вычисления площади трапеции по этим данным:
Пусть дана трапеция с основаниями а = 3 см, b = 7 см и стороны с = 5 см, d = 4 см. Найдите площадь фигуры:
Площадь равнобедренной трапеции
Отдельным случаем является равнобедренная или, как ее еще называют, равнобедренная трапеция.
Частным случаем является также нахождение площади равнобедренной (равнобедренной) трапеции. Формулы выводятся разными способами — через диагонали, через углы, прилежащие к основанию, и через радиус вписанной окружности.
Если длина диагоналей задана условиями и известен угол между ними, то можно воспользоваться следующей формулой:
Помните, что диагонали равнобедренной трапеции равны между собой!
То есть, зная одно их основание, сторону и угол, можно легко вычислить площадь.
Площадь криволинейной трапеции
Отдельным случаем является криволинейная трапеция . Он расположен на оси координат и ограничен графиком непрерывной положительной функции.
Его основание расположено на оси X и ограничено двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула записывается так:
Рассмотрим пример вычисления площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Сначала проанализируем значение определенного интеграла:
Сначала проанализируем значение определенного интеграла:
Здесь F(a) — значение первообразной функции f(x) в точке a , F(b) — значение той же функции f(x) в точке б .
Теперь решим задачу. На рисунке показана криволинейная трапеция, функция ограничена. Функция
Нам нужно найти площадь выбранной фигуры, представляющей собой криволинейную трапецию, ограниченную сверху графиком, справа прямая х = (-8), слева прямая х = (-10) и ось OX ниже.
Вычислим площадь этой фигуры по формуле:
Нам задана функция по условиям задачи. С его помощью найдем значения первообразной в каждой нашей точке:
Теперь
Ответ: площадь данной криволинейной трапеции равна 4.
В вычислении этой величины нет ничего сложного. Важна только предельная аккуратность в расчетах.
Трапеция – определение, свойства, формулы и примеры
Трапеция – определение, свойства, формулы и примерыСодержание
Последнее изменение: 6 сентября 2022 г.
Оглавление
Определение
Трапеция — это плоская геометрическая фигура с четырьмя прямыми сторонами, имеющая по крайней мере одну пару противоположных параллельных сторон. Он выглядит как треугольник, верхняя часть которого срезана.
Параллельные стороны являются основаниями, а две другие стороны называются ножками или боковыми сторонами. Его также называют трапецией в Великобритании и некоторых других частях мира.
ТрапецияСвойства
Свойства трапеции- Имеет четыре стороны и четыре угла; в трапеции ABCD стороны AB, BC, CD и DA составляют углы ∠DAB, ∠ABC, ∠BCD и ∠CDA, равные 9.
 0012
0012 - Имеет одну пару параллельных сторон. Две параллельные стороны — это основания, а непараллельные стороны — это ножки; здесь AD = короткое основание, BC = длинное основание, тогда как AB = отвод 1 и CD = отвод 2, и AD ∥ BC
- Смежные углы в сумме составляют 180°; таким образом, ∠DAB + ∠ABC = 180°, ∠ABC + ∠BCD = 180°, ∠BCD + ∠CDA = 180° и ∠CDA + ∠DAB = 180°
- Медиана параллельна двум основаниям и делит непараллельные стороны на две равные части; поэтому EF ∥ AD и EF ∥ BC
Формулы
Медиана
Это отрезок посередине между двумя основаниями. Ее также называют средней линией или средним сегментом. Формула приведена ниже:
Медиана трапецииНайдите медиану трапеции с основаниями 7 м и 9 м.
Решение:
Как мы знаем,
Медиана ( M ) = ½ ( A + B ) , здесь A = ) . (9+ 7) м
= 16/2 м
= 8 м
Площадь
Общая площадь трапеции. Формула приведена ниже:
Формула приведена ниже:
Найдите площадь трапеции, если два основания 8 см и 6 см, а высота 10 см
Решение:
A ) = ½ ( a + b ) × h , здесь a = 8 см, b = 6 см и h = 10 см0540 = 1/2 × (8 + 6) × 10 см 2
= ½ × 14 × 10 см 2
= 70 см 2
: 9053 когда известны МЕДИАНА и ВЫСОТА
Найдите площадь трапеции с медианой 5 см и высотой 11 см
20 ,
А = M × H , здесь M = медиана и H = высота
в этом трапеце. h
= 5 × 11 см 2
= 55 см 2
Периметр
Общее расстояние, пройденное по краю трапеции. Формула приведена ниже:
Найдите периметр трапеции со сторонами 6 м, 8 м, 12 м и 15 м.

 02.16
02.16

 Средняя линия параллельна основаниям трапеции и равна их полусумме.
Средняя линия параллельна основаниям трапеции и равна их полусумме.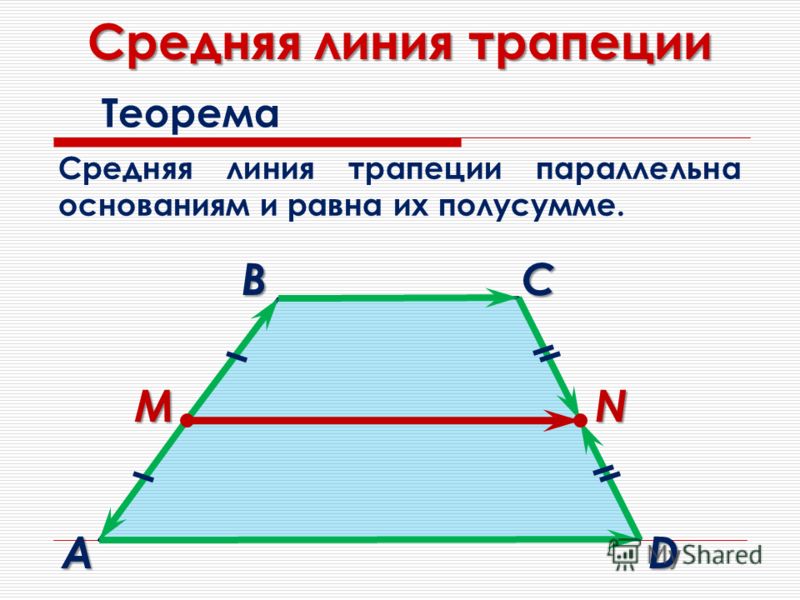 Его длина
Его длина 0012
0012