Ответ. $\begin{aligned} \cos \phi=\frac{14}{15} \end{aligned}$
Читать дальше: как найти скалярное произведение векторов.
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
03.21
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Периметр правильного треугольника, вписанного в окружность, равен 6√3 дм.
Найдите периметр правильного шестиугольника описанного около той же окружности.
Здравствуйте! Прошу помощи! Алеша сказал: «У Змея Горыныча больше трех голов». Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше
Решено
Начертите треугольник АВС. Постройте вектор: 1) АС+СВ 2)ВА-ВС 3)АС+АВ
На окружности с центром в точке О по порядку отмечены 4 точки: D, H, L, P. Найди вторую сторону получившегося четырехугольника, если угол D=90
вишнёвом сиропе фирмы «Аграрий» содержится 30 % сахара, в малиновом сиропе фирмы «Мишка» — 50 %, фирма «Солнышко» производит сироп из клюквы с
Пользуйтесь нашим приложением
Угол между двумя векторами Формула
Векторная величина – это физическая величина, имеющая как величину, так и направление. Когда на частицу действуют два вектора, результирующее действие на частицу будет зависеть от угла между этими векторами.
Поэтому важно знать угол между ними.
Некоторые свойства вектора для вычисления угла
Вектор представлен стрелкой, параллельной направлению вектора.
- Вектор остается неизменным, если он передается параллельно самому себе.
- Два вектора, имеющие одинаковое направление, являются параллельными векторами.
- Два вектора, имеющие противоположные направления, являются антипараллельными векторами.
- Два вектора, имеющие одинаковую величину и направление, являются равными векторами.
- Два вектора, имеющие одинаковую величину и противоположное направление, называются отрицательными векторами.
Скалярное произведение
Также известно как скалярное произведение векторов. У него есть только величина, но нет направления.
Два вектора А и В
Тогда скалярное произведение A и B определяется как,
= |A| |Б| cosθ.
Особые случаи
- Когда угол между векторами равен 0 градусов.
То есть θ = 0°
⇒ |A| |Б| cosθ.
⇒ |А| |Б| cos0°
⇒ |А| |Б| [cos0° = 1]
- Когда угол между векторами равен 180 градусов.
⇒ |А| |Б| cosθ.
⇒ |А| |Б| cos180°
⇒ – |A| |Б| [cos180° = -1]
- Когда угол между векторами равен 90 градусов.
⇒ |А| |Б| cosθ.
⇒ |А| |Б| cos90°
⇒ |А| |Б| × 0 [cos90° = 0]
⇒ 0,
Формула для угла между двумя векторами
Косинус угла между двумя векторами равен сумме произведений отдельных составляющих двух векторов, разделенных произведением величины двух векторов.
Два вектора A и B
=| А | | Б | cosθ.
cosθ=
θ= cos -1
В декартовой форме,
A = A x i + A y j + A z k
B= B x 8 9 j0 90890 i8 + B x 0 i8 г k
cosθ =
Свойства скалярного произведения
- Скалярное произведение коммутативно.
- Дополнительный продукт является распределительным.
В физике при конвекции угол между двумя векторами лежит между 0 ≤ θ ≤ 180. Когда хвосты или вершины обоих векторов совпадают, вычисляется угол между векторами.
Хвост совпадает
Голова совпадает
Примеры задач
Вопрос 1. Найдите угол между векторами (если они образуют равносторонний треугольник) 5 b и c векторы
Равносторонний треугольник, образованный векторами а, b, с
Решение:
- Векторы а и b друг друга, следовательно, угол между векторами a и b равен углу между двумя сторонами равностороннего треугольника = 60°.
- Векторы b и c:
Из рисунка выше видно, что начало или конец векторов b и c не совпадают друг с другом.
Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
Вектор c смещен параллельно самому себе
Теперь мы видим, что хвосты векторов b и c совпадают друг с другом, следовательно, такой же, как внешний угол при равностороннем треугольнике = 120°.
- Векторы а и с
Хвост векторов а и с совпадает
Для векторов а и с хвосты обоих векторов совпадают, следовательно, угол между векторами а и с равен углу между Две стороны равностороннего треугольника = 60°.
Вопрос 2: Найдите углы между векторами, если они образуют равнобедренный прямоугольный треугольник.
- вектор a и b
- вектор b и c
- векторы a и c
Решение:
- вектор a и b
Прямоугольный равнобедренный треугольник
Из приведенного выше рисунка видно, что вершина и хвост вектора a не совпадают. друг с другом. Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
вектор сдвинут параллельно самому себе
Теперь хвосты векторов a и b совпадают и образуют угол, равный внешнему углу прямоугольного равнобедренного треугольника = 135°.
- Векторы b и c
Прямоугольный равнобедренный треугольник
На приведенном выше рисунке вершина или решка векторов b и c не совпадают. Таким образом, при использовании свойства вектор остается неизменным, если он передается параллельно самому себе.
Вектор b смещен параллельно самому себе
Теперь хвосты векторов b и c совпадают и составляют угол, равный внешнему углу прямоугольного равнобедренного треугольника = 135°.
- Векторы a и c
Прямоугольный равнобедренный треугольник
Из приведенного выше рисунка видно, что вершина или решка векторов a и c не совпадают. Итак, с помощью свойства- Вектор остается неизменным, если он передается параллельно самому себе.
Вектор c перемещается параллельно самому себе
Теперь хвосты векторов a и c совпадают и составляют угол, равный прямому углу равнобедренного треугольника = 90°.
Вопрос 3: Найдите угол между векторами A = i + j + k и вектором B = -2i – 2j – 2k.
Решение:
Из формулы
A = A x i + A y j + A z k 90 8 8 B = 90 0 8 B 90 0 0 8 B = 9 0 8 B 8 B 0 9 0 я + В г й + B z k
cosθ=
Здесь в заданном вопросе
A= i + j + k.
В= -2i -2j -2k.
Подставляя значения в формулу
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°.
Вопрос 4. Найдите угол между векторами A = 3i + 4j и B = 2i + j
Решение:
k
B = B x i + B y j + B z k
cosθ =
Здесь дано,
A= 2 0 3 я + j + 0k
Подставляя значения в формулу,
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ θ = cos 90⇒002 -1
() θ = cos -1 ()
Вопрос 5 : Найдите угол между вектором A = i + j и вектором B = j + k.
Решение:
Из формулы
A = A x i + A y j + A z k 9008 B = 8
B = 8
3 90 9 я + В г й + В с k
cosθ =
Здесь в заданном вопросе
⇒ A = i + j
⇒ B = j + k
⇒ cosθ = 0 9 θ 0 9 θ
⇒ 9000 co
⇒ cosθ =.
⇒ θ = cos -1 (1/2)
⇒ θ = 60°.
Калькулятор угла между двумя векторами Просто введите компоненты каждого вектора в форме
Как найти угол между двумя векторами
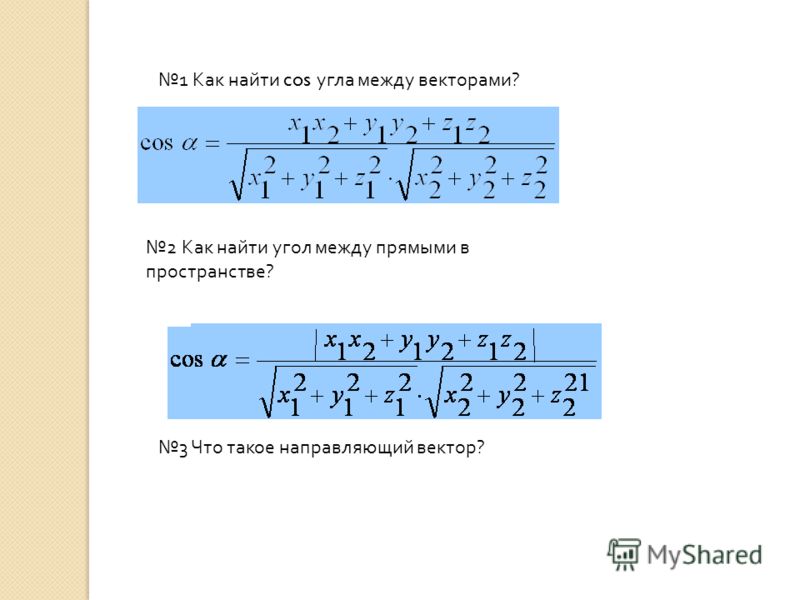
Чтобы найти угол между двумя векторами:
- Найдите скалярное произведение двух векторов.
- Разделите это значение на величину первого вектора.
- Разделите это значение на величину второго вектора.
- Возьмите арккосинус этого значения, чтобы получить угол.
Например, найдите угол между и .
Шаг 1.
Чтобы найти скалярное произведение двух векторов, умножьте соответствующие компоненты и сложите их.
Скалярное произведение двух двумерных векторов и находится с помощью .
Для векторов и скалярное произведение .
Поэтому
(3\-2)” role=”presentation” style=”font-size: 113%; position: relative;»>
Шаг 2. Разделите это на величину первого вектора
Чтобы вычислить величину вектора, используйте теорему Пифагора с компонентами 𝑥 и y вектора.
Величина любого вектора находится следующим образом: .
Следовательно, величина вектора равна .
Это становится который есть .
Величина первого вектора, a равна .
Мы делим скалярное произведение, рассчитанное ранее, на эту величину.
Получаем
Шаг 3. Разделим на величину второго вектора
Величина второго вектора b находится с помощью .
Для вектора величина равна .
Это становится то, что есть .
Мы делим предыдущий результат на эту величину, чтобы получить
Шаг 4. Возьмем арккосинус этого результата
Формула для нахождения угла между двумя векторами: .
Это можно преобразовать, взяв значение, обратное косинусу в обеих частях уравнения.
Угол между двумя векторами равен .
Как было рассчитано ранее:
Используя калькулятор, мы вводим, .
Это дает нам угол между двумя векторами как .
Формула угла между двумя векторами
Формула для угла между двумя векторами a и b равна θ=cos -1 ( a•b / |a||b| 90) . Где вектор a равен (a x a y ), а вектор b равен (b x b y ), скалярное произведение a•b=a x х + а у б у .
6 ) и модуль вектора 06
( б х 2 + б у 2 ).Наиболее распространенное отображение формулы для угла между двумя векторами показано ниже как .
Эту формулу можно преобразовать в более удобную формулу, взяв арккосинус обеих частей уравнения.
Это дает нам прямую формулу для угла между двумя векторами.
Угол между двумя векторами равен .
Мы можем использовать эту формулу, чтобы найти угол между двумя векторами в 2D.
Найдите угол между векторами и .
В этих двух векторах a x = 2, a y = 5, b x = -4 и b г = -1.
Скалярное произведение находится с помощью , которое для наших векторов становится и так .
Величина каждого вектора находится с помощью теоремы Пифагора с компонентами 𝑥 и y.
Для этих векторов и т.д. и так .
Теперь можно использовать формулу.
и это можно оценить прямо на калькуляторе, чтобы дать.
Как найти угол между двумя векторами в 3D
Чтобы найти угол между двумя векторами в 3D:
- Найдите скалярное произведение векторов.
- Разделите скалярное произведение на величину каждого вектора.
- Используйте инверсию косинуса к этому результату.
Например, найдите угол между и .
Эти векторы содержат компоненты в трех измерениях: 𝑥, y и z.
Для вектора a x = 2, a y = -1 и a z = 3.
Для вектора b x = 2, b y = 0 и b 00088 z = 1.
Шаг 1. Найдите скалярное произведение векторов
Чтобы найти скалярное произведение двух векторов, умножьте соответствующие компоненты каждого вектора и сложите результаты.
Для вектора в 3D .
Для наших векторов это становится .
Это упрощается до .
Шаг 2. Разделите это скалярное произведение на величину двух векторов
Чтобы найти величину вектора в 3D, используйте теорему Пифагора. Например, .
Для вектора , . Это упрощает до .
Для вектора , . Это упрощает до .
Мы делим скалярное произведение, найденное на шаге 1, на обе эти величины.
Получаем .
Шаг 4. Используйте обратный косинус для этого результата
Формула для угла между двумя векторами: . Эту формулу можно использовать для векторов в 2D или 3D.
Чтобы изменить эту формулу для угла, мы берем арккосинус обеих сторон.
Ранее мы рассчитали , и .
Поэтому .
Это можно оценить на калькуляторе, чтобы получить угол между двумя векторами как .
Что говорит нам о векторах знак cosθ?
Если значение cosθ положительное, угол между векторами острый.
Как определить, перпендикулярны ли два вектора
Два вектора перпендикулярны, если их скалярное произведение равно нулю. Для двух векторов (a x a y ) и (b x b y ), скалярное произведение равно a•b =
5
б х + а у б у . Если a x
b x + a y b y , то два вектора перпендикулярны. Это означает, что они встречаются под прямым углом. Формула для угла между двумя векторами имеет вид .
Если , то эта формула принимает вид .
Если числитель дроби равен нулю, то вся дробь равна нулю. Поэтому формула становится .
Решая это для угла, мы используем арккосинус нуля, .
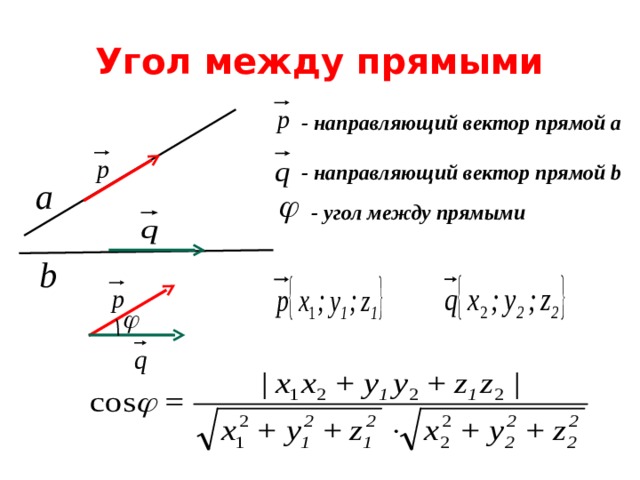
Найдите скалярное произведение двух векторов 
Величина вектора |a|=√ ( a x 2 + a y 2 
Если значение cosθ отрицательно, угол между векторами тупой. 