Показатели вариации в статистике решение задач: Задача №6. Расчёт показателей вариации

404 Cтраница не найдена

Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.

Размер:

AAA

Изображения Вкл. Выкл.

Обычная версия сайта

К сожалению запрашиваемая страница не найдена.

Но вы можете воспользоваться поиском или картой сайта ниже

Университет Майкопский государственный технологический университет – один из ведущих вузов юга России. История университета Анонсы Объявления Медиа Представителям СМИ Газета «Технолог» О нас пишут Ректорат Структура Филиал Политехнический колледж Медицинский институт Лечебный факультет Педиатрический факультет Фармацевтический факультет Стоматологический факультет Факультет послевузовского профессионального образования Факультеты Кафедры Ученый совет Дополнительное профессиональное образование Бережливый вуз – МГТУ Новости Объявления Лист проблем Лист предложений (Кайдзен) Реализуемые проекты Архив проектов Фабрика процессов Рабочая группа «Бережливый вуз-МГТУ» Вакансии Профсоюз Противодействие терроризму и экстремизму Противодействие коррупции WorldSkills в МГТУ Научная библиотека МГТУ Реквизиты и контакты Управление имущественным комплексом Опрос в целях выявления мнения граждан о качестве условий оказания образовательных услуг Работа МГТУ в условиях предотвращения COVID-19 Документы, регламентирующие образовательную деятельность Система менеджмента качества университета Региональный центр финансовой грамотности Аккредитационно-симуляционный центр Абитуриентам Подача документов онлайн Абитуриенту 2023 Экран приёма 2022 Иностранным абитуриентам Международная деятельность Общие сведения Кафедры Новости Центр международного образования Академическая мобильность и международное сотрудничество Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Как стать участником программ академической мобильности Дни открытых дверей в МГТУ День открытых дверей online Университетские субботы Дни открытых дверей на факультетах Подготовительные курсы Подготовительное отделение Курсы для выпускников СПО Курсы подготовки к сдаче ОГЭ и ЕГЭ Онлайн-курсы для подготовки к экзаменам Подготовка школьников к участию в олимпиадах Малая технологическая академия Профильный класс Социально-экономический профиль Медико-фармацевтический профиль Инженерно-технологический профиль Эколого-биологический профиль Агротехнологический профиль Индивидуальный проект Кружковое движение юных технологов Олимпиады, конкурсы, фестивали Веб-консультации для абитуриентов и их родителей Веб-консультации для абитуриентов Родительский университет Олимпиады для школьников Отборочный этап Заключительный этап Итоги олимпиад Профориентационная работа Стоимость обучения Студентам Студенческая жизнь Стипендии Организация НИРС в МГТУ Студенческое научное общество Студенческие научные мероприятия Конкурсы Академическая мобильность и международное сотрудничество Образовательные программы Расписание занятий Расписание звонков Онлайн-сервисы Социальная поддержка студентов Общежития Трудоустройство обучающихся и выпускников Вакансии Обеспеченность ПО Инклюзивное образование Условия обучения лиц с ограниченными возможностями Доступная среда Ассоциация выпускников МГТУ Перевод из другого вуза Вакантные места для перевода Студенческое пространство Студенческое пространство Запись на мероприятия Отдел по социально-бытовой и воспитательной работе

Наука и инновации Научная инфраструктура Проректор по научной работе и инновационному развитию Научно-технический совет Управление научной деятельностью Управление аспирантуры и докторантуры Точка кипения МГТУ О Точке кипения МГТУ Руководитель и сотрудники Документы Контакты Центр коллективного пользования Центр народной дипломатии и межкультурных коммуникаций Студенческое научное общество Новости Научные издания Научный журнал «Новые технологии» Научный журнал «Вестник МГТУ» Научный журнал «Актуальные вопросы науки и образования» Публикационная активность Конкурсы, гранты Научные направления и результаты научно-исследовательской деятельности Основные научные направления университета Отчет о научно-исследовательской деятельности в университете Результативность научных исследований и разработок МГТУ Финансируемые научно-исследовательские работы Объекты интеллектуальной собственности МГТУ Результативность научной деятельности организаций, подведомственных Минобрнауки России (Анкеты по референтным группам) Студенческое научное общество Инновационная инфраструктура Федеральная инновационная площадка Проблемные научно-исследовательские лаборатории Научно-исследовательская лаборатория «Совершенствование системы управления региональной экономикой» Научно-исследовательская лаборатория проблем развития региональной экономики Научно-исследовательская лаборатория организации и технологии защиты информации Научно-исследовательская лаборатория функциональной диагностики (НИЛФД) лечебного факультета медицинского института ФГБОУ ВПО «МГТУ» Научно-исследовательская лаборатория «Инновационных проектов и нанотехнологий» Научно-техническая и опытно-экспериментальная база Центр коллективного пользования Научная библиотека Экспортный контроль Локальный этический комитет Конференции Международная научно-практическая конференция фундаментальные и прикладные аспекты геологии, геофизики и геоэкологии с использованием современных информационных технологий Международная научно-практическая конференция «Актуальные вопросы науки и образования» VI Международная научно-практическая онлайн-конференция Наука и университеты Международная деятельность Иностранным студентам Международные партнеры Академические обмены, иностранные преподаватели Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Факультет международного образования Новости факультета Информация о факультете Международная деятельность Кафедры Кафедра русского языка как иностранного Кафедра иностранных языков Центр Международного образования Центр обучения русскому языку иностранных граждан Приказы и распоряжения Курсы русского языка Расписание Академическая мобильность Контактная информация Контактная информация факультета международного образования Сведения об образовательной организации Основные сведения Структура и органы управления образовательной организацией Документы Образование Образовательные стандарты и требования Руководство. Педагогический (научно-педагогический) состав Материально-техническое обеспечение и оснащённость образовательного процесса Стипендии и меры поддержки обучающихся Платные образовательные услуги Финансово-хозяйственная деятельность Вакантные места для приёма (перевода) Международное сотрудничество Доступная среда Организация питания в образовательной организации

Карта сайта

1. Главная
2. vikon

Об университете Миссия университета История университета Антитеррор Информационная безопасность Система менеджмента качества Документы СМК Партнеры События университета (Новости) Приёмная комиссия События Анонсы событий Пресс-релизы Сми о нас Символика университета Контакты Структура Руководство Структурные подразделения Институты и факультеты Деятельность Приемная комиссия Приемная комиссия Довузовская подготовка Оценка качества образования Внутренняя система оценки качества образования Независимая оценка качества образования Независимая оценка качества подготовки обучающихся Независимая оценка качества условий осуществления образовательной деятельности Общественная аккредитация. Профессионально-общественная аккредитация Студенческая жизнь Внеучебная деятельность Волонтерская деятельность Социально-культурная деятельность Совет студентов и аспирантов ПВГУС Новости и события Архив новостей Афиша мероприятий Почетные студенты ПВГУС Памятка молодому избирателю История достижений ЦВД Наука Управление научных исследований Аспирантура Диссертационный совет Студенческое научное общество Новостная лента СНО Стипендии Научные школы Конференции ГРАНТОВО-ПРОЕКТНАЯ ДЕЯТЕЛЬНОСТЬ Издательская деятельность Издательско-полиграфический центр English version Научные издания Лицензионный договор Справочная информация Международная деятельность Дополнительное образование Противодействие коррупции За здоровый образ жизни! Демонстрационный экзамен Национальный проект «Наука и университеты» Стоп коронавирус Федеральная инновационная площадка Сведения об образовательной организации Основные сведения Структура и органы управления образовательной организацией Документы Образование Образовательные стандарты и требования Руководство. Педагогический (научно-педагогический) состав Материально-техническое обеспечение и оснащённость образовательного процесса Стипендии и меры поддержки обучающихся Платные образовательные услуги Финансово-хозяйственная деятельность Вакантные места для приема (перевода) обучающихся Доступная среда Международное сотрудничество

Сервисы Расписание Электронная библиотечная система Ход образовательного процесса Телефонный справочник Обратная связь Контакты Личный кабинет обучающегося

Показатели изменчивости

Посмотрите на два набора данных в таблице 2.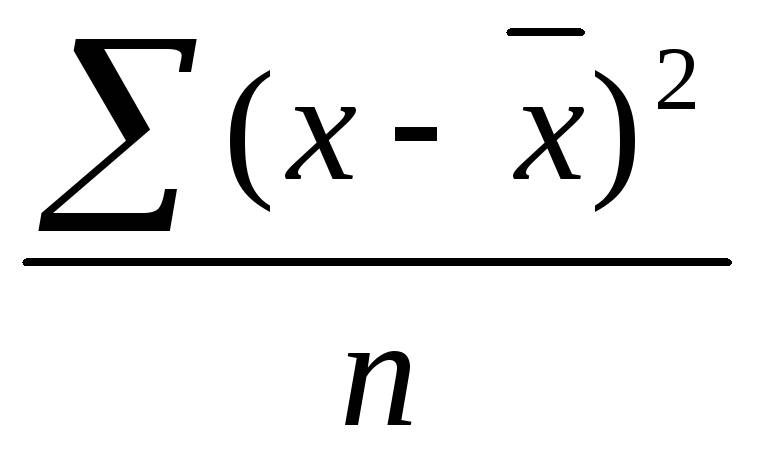 1 «Два набора данных» и графическое представление каждого из них, называемое точечным графиком , на рисунке 2.10 «Точечные графики наборов данных».

Два набора из десяти измерений центрируются на одном и том же значении: они оба имеют среднее значение, медиану и моду 40. Тем не менее, взгляд на рисунок показывает, что они заметно различаются. В наборе данных I измерения лишь незначительно отличаются от центра, в то время как в наборе данных II измерения сильно различаются. Точно так же, как мы привязывали числа к набору данных, чтобы найти его центр, теперь мы хотим связать с каждым набором данных числа, которые количественно измеряют, как данные либо рассеиваются от центра, либо группируются близко к нему. Эти новые величины называются мерами изменчивости, и мы обсудим три из них.

Диапазон

Первая мера изменчивости, которую мы обсуждаем, является самой простой.

Определение

Диапазон Изменчивость набора данных, измеряемая числом R=xmax−xmin. набора данных — это число R , определенное по формуле

R=xmax−xmin

, где xmax — наибольшее измерение в наборе данных, а xmin — наименьшее.

Пример 10

Найдите диапазон каждого набора данных в таблице 2.1 «Два набора данных».

Решение:

Для набора данных I максимальное значение равно 43, а минимальное значение равно 38, поэтому диапазон составляет R=43−38=5.

Для набора данных II максимальное значение равно 47, а минимальное значение равно 33, поэтому диапазон составляет R=47−33=14.

Диапазон является мерой изменчивости, поскольку он указывает размер интервала, по которому распределены точки данных. Меньший диапазон указывает на меньшую изменчивость (меньшую дисперсию) среди данных, тогда как больший диапазон указывает на обратное.

Дисперсия и стандартное отклонение

Две другие меры изменчивости, которые мы рассмотрим, являются более сложными и также зависят от того, является ли набор данных просто выборкой, взятой из гораздо большей совокупности, или представляет собой всю совокупность как таковую (т. , перепись).

Определение

Выборочная дисперсия набора n Выборочные данные — это число s ^{3 3 900 формула0004}

s2=Σ(x−x-)2n−1

, что по алгебре эквивалентно формуле

s2=Σx2−1n(Σx)2n−1

Изменчивость стандартного отклонения выборочные данные, измеренные числом Σ(x−x-)2n−1. набора n выборочных данных представляет собой квадратный корень выборочной дисперсии, следовательно, число s определяется формулами

s=Σ(x−x-)2n−1= Σx2−1n(Σx)2n−1

Хотя первая формула в каждом случае выглядит менее сложной, чем вторая, последнюю легче использовать в ручных вычислениях, и она называется

.0055 формула быстрого доступа .

Пример 11

Найдите выборочную дисперсию и выборочное стандартное отклонение набора данных II в таблице 2. 1 «Два набора данных».

Решение:

Чтобы использовать определяющую формулу (первую формулу) в определении, мы сначала вычисляем для каждого наблюдения x его отклонение x−x- от выборочного среднего. Поскольку среднее значение данных равно x-=40, мы получаем десять чисел, отображаемых во второй строке прилагаемой таблицы.

x46374033423640473445x-x-6-30-72-407-65

Затем

Σ(x−x-)2=62+(−3)2+02+(−7)2+22+(−4)2+02+72+(−6)2+52= 224

, поэтому

s2=Σ(x−x-)2n−1=2249=24,8-

и

s=24,8-≈4,99

Студенту предлагается вычислить десять отклонений для набора данных I и убедитесь, что сумма их квадратов равна 20, так что выборочная дисперсия и стандартное отклонение набора данных I представляют собой гораздо меньшие числа s2=20/9=2,2- и s=20/9≈1,49.

Пример 12

Найдите выборочную дисперсию и выборочное стандартное отклонение десяти GPA в примечании 2. 12 «Пример 3» в разделе 2.2 «Показатели центрального местоположения».

1.903.002.533.712.121.762.711.394.003.33

Решение:

С

σx = 1,90+3,00+2,53+3,71+2,12+1,76+2,71+1,39+4.00+3,33 = 26,45292222 и 2,71+9.39+4.00+3,33 = 26,4522 и 2,71+9,39+4,00+3,33 = 26,452 9000 и 2,712 и 2,71. Σ​x2=1,902+3,002+2,532+3,712+2,122+1,762+2,712+1,392+4,002+3,332=76,7321

сокращенная формула дает

s2=Σx2−1n(Σx)2n−1=76,76,7 21010−1=6,771859=0,752427-

и

s=0,752427-≈0,867

Выборочная дисперсия отличается от данных. Например, если единицами измерения в наборе данных были дюймы, новые единицы измерения будут квадратными дюймами или квадратными дюймами. Таким образом, это имеет прежде всего теоретическое значение и не будет рассматриваться далее в этом тексте, кроме как вскользь.

Если набор данных включает всю совокупность, то определяется стандартное отклонение совокупности , обозначаемое σ (строчная греческая буква сигма), и его квадрат, дисперсия совокупности σ ² . следующее.

Определение

дисперсия населения и стандартное отклонение населения Изменчивость данных населения, измеряемая числом σ2=Σ(x−μ)2N. комплекта из 9 штук0004 N Данные популяции являются числа σ ² и σ , определяемые формулами

σ = σ (x — μ) 2n и σ = σ (x -μ) 2n.

Обратите внимание, что знаменатель дроби представляет собой полное число наблюдений, а не число, уменьшенное на единицу, как в случае стандартного отклонения выборки. Поскольку большинство наборов данных являются выборками, мы всегда будем работать со стандартным отклонением и дисперсией выборки.

Наконец, во многих реальных ситуациях наиболее важные статистические вопросы связаны со сравнением средних значений и стандартных отклонений двух наборов данных. Рисунок 2.11 «Разница между двумя наборами данных» иллюстрирует, как разница в одном или обоих из среднего значения выборки и стандартного отклонения выборки отражается на внешнем виде набора данных, как показано кривыми, полученными из гистограмм относительной частоты, построенных с использованием данных. .

Рисунок 2.11 Разница между двумя наборами данных

Основные выводы

Диапазон, стандартное отклонение и дисперсия дают количественный ответ на вопрос «Насколько изменчивы данные?»

Упражнения

Базовый

1. Найдите диапазон, дисперсию и стандартное отклонение для следующей выборки.

   1 2 3 4

2. Найдите диапазон, дисперсию и стандартное отклонение для следующей выборки.

   2 −3 6 0 3 1

3. Найдите диапазон, дисперсию и стандартное отклонение для следующей выборки.

   2 1 2 7

4. Найдите диапазон, дисперсию и стандартное отклонение для следующей выборки.

   −1 0 1 4 1 1

5. Найдите диапазон, дисперсию и стандартное отклонение для выборки, представленной таблицей частот данных.

   x127f121

6. Найдите диапазон, дисперсию и стандартное отклонение для выборки, представленной таблицей частот данных.

   х-1014f1131

Приложения

7. Найдите диапазон, дисперсию и стандартное отклонение для выборки из десяти показателей IQ, случайно выбранных в школе для академически одаренных учащихся.

   132162133145148139147160150153

8. Найдите диапазон, дисперсию и стандартное отклонение для выборки из десяти баллов IQ, случайно выбранных из школы для академически одаренных учащихся.

   142152138145148139147155150153

Дополнительные упражнения

9. Рассмотрим набор данных, представленный таблицей

   x26272829303132f341612621

   1. Используйте таблицу частот, чтобы найти, что Σx=1256 и Σx2=35 926.
   2. Используйте информацию в части (a) для вычисления среднего значения выборки и стандартного отклонения выборки.

10. Найдите стандартное отклонение выборки для данных

    x12345f384208985628x678910f128231

11. Произведена случайная выборка из 49 накладных на ремонт в автомастерской. Данные сгруппированы на показанной диаграмме стебля и листа. (Стебли стоят тысячи долларов, листья — сотни, так что, например, самое большое наблюдение — 3800.)

    3568300112425667788992000012241555667778834440568804

    Для этих данных Σx=101 100, Σx2=244 830 000.

    1. Вычислить среднее значение, медиану и моду.
    2. Вычислить диапазон.
    3. Вычислите стандартное отклонение выборки.

12. Что должно быть верно для набора данных, если его стандартное отклонение равно 0?

13. Набор данных, состоящий из 25 измерений, имеет стандартное отклонение 0. Одно из измерений имеет значение 17. Каковы остальные 24 измерения?

14. Создайте выборочный набор данных размером n = 3, для которого диапазон равен 0, а среднее значение выборки равно 2.

15. Создать выборочный набор данных размером n = 3, для которого выборочная дисперсия равна 0, а выборочное среднее равно 1.

16. Выборка {−1,0,1} имеет среднее значение x-=0 и стандартное отклонение s = 1. Создайте набор выборочных данных размером n = 3, для которого x-=0 и s больше чем 1.

17. Выборка {−1,0,1} имеет среднее значение x-=0 и стандартное отклонение s = 1. Создайте набор выборочных данных размером n = 3, для которого x-=0 и стандартное отклонение с меньше 1.

18. Начните со следующего набора данных, назовите его Набор данных I.

    5-2614-3014325

    1. Вычислите выборочное стандартное отклонение набора данных I.
    2. Сформируйте новый набор данных, набор данных II, добавив 3 к каждому числу в наборе данных I. Рассчитайте выборочное стандартное отклонение набора данных II.
    3. Сформируйте новый набор данных, набор данных III, вычитая 6 из каждого числа в наборе данных I. Рассчитайте выборочное стандартное отклонение набора данных III.
    4. Сравнив ответы к пунктам (а), (б) и (в), сможете ли вы угадать закономерность? Сформулируйте общий принцип, который, как вы ожидаете, будет верным.

Упражнения с большими наборами данных

19. Большой набор данных 1 содержит результаты SAT и средний балл 1000 учащихся.

    http://www.gone.2012books.lardbucket.org/sites/all/files/data1.xls

    1. Вычислить диапазон и выборочное стандартное отклонение 1000 баллов SAT.
    2. Вычислите диапазон и стандартное отклонение выборки для 1000 GPA.

20. Большой набор данных 1 содержит результаты SAT 1000 учащихся.

    http://www.gone.2012books.lardbucket.org/sites/all/files/data1.xls

    1. Считать данные полученными в результате переписи всех учащихся средней школы, в которой балл SAT измеряли каждого ученика. Вычислить диапазон населения и стандартное отклонение населения о .
    2. Считайте первые 25 наблюдений случайной выборкой, взятой из этой совокупности. Вычислите диапазон выборки и стандартное отклонение выборки s и сравните их с диапазоном совокупности и σ .
    3. Считайте следующие 25 наблюдений случайной выборкой из этой совокупности. Вычислите диапазон выборки и стандартное отклонение выборки s и сравните их с диапазоном генеральной совокупности и о .

21. Большой набор данных 1 содержит средний балл 1000 учащихся.

    http://www.gone.2012books.lardbucket.org/sites/all/files/data1.xls

    1. Рассматривайте данные как полученные в результате переписи всех первокурсников небольшого колледжа в конце их первого академического год обучения в колледже, в течение которого измерялся средний балл каждого такого человека. Вычислить диапазон населения и стандартное отклонение населения о .
    2. Считайте первые 25 наблюдений случайной выборкой, взятой из этой совокупности. Вычислите диапазон выборки и стандартное отклонение выборки s и сравните их с диапазоном совокупности и σ .
    3. Считайте следующие 25 наблюдений случайной выборкой из этой совокупности. Вычислите диапазон выборки и стандартное отклонение выборки s и сравните их с диапазоном генеральной совокупности и о .
22. В больших наборах данных

    7, 7A и 7B указано время выживания в днях 140 лабораторных мышей с лейкемией тимуса от начала до смерти.

    http://www.gone.2012books.lardbucket.org/sites/all/files/data7.xls

    http://www.gone.2012books.lardbucket.org/sites/all/files/data7A.xls

    http://www.gone.2012books.lardbucket.org/sites/all/files/data7B.xls

    1. Рассчитайте диапазон и стандартное отклонение выборки времени выживания для всех мышей, независимо от пола.
    2. Вычислите диапазон и стандартное отклонение выборки времени выживания для 65 самцов мышей (отдельно записанных в большом наборе данных 7A).
    3. Вычислите диапазон и стандартное отклонение выборки времени выживания для 75 самок мышей (отдельно записанных в большом наборе данных 7B). Вы видите разницу в результатах для самцов и самок мышей? Это кажется значительным?

Ответы

1. R = 3, с ² = 1,7, с = 1,3.

3. R = 6, s2=7,3-, s = 2,7.

5. R = 6, с ² = 7,3, с = 2,7.

7. R = 30, с ² = 103,2, с = 10,2.

9. х-=28,55, с = 1,3.

11. 1. х-=2063, х~=2000, режим=2000.
    2. Р = 3400.
    3. с = 869.

13. Все 17.

15. {1,1,1}

17. Одним из примеров является {−.5,0,.5}.

19. 1. R = 1350 и с = 212,5455
    2. R = 4,00 и с = 0,7407
21. 1. R = 4,00 и σ = 0,740375
    2. р = 3,04 и с = 0,808045
    3. R = 2,49 и с = 0,657843

Решения задач дисперсии и стандартного отклонения

В этом разделе вы найдете определения дисперсии и стандартного отклонения, а также их формулы. Кроме того, мы предоставим вам практические задачи, чтобы вы могли усовершенствовать или освежить свои знания по этим 9 упражнениям.0055 мощные меры изменчивости. В других разделах этого руководства по описательной статистике вы узнаете, как эти меры применяются на более сложном уровне, например, как интерпретировать каждую меру и в каких ситуациях следует использовать дисперсию вместо стандартного отклонения.

Лучшие репетиторы по математике

Поехали

Показатели изменчивости

Как мы обсуждали ранее, описательную статистику можно разбить на две отдельные меры: показатели центральной тенденции и показатели изменчивости. В то время как меры центральной тенденции пытаются уловить центр данных, меры изменчивости стремятся идентифицируют уровень вариации данных, также известный как спред. Распространение данных — это простая для запоминания концепция, поскольку акт распространения идет рука об руку со своим аналогом в статистике.

Распространение данных позволяет нам узнать, сгруппированы ли точки данных близко друг к другу, разбросаны ли они далеко друг от друга, есть ли какие-то точек, сгруппированных вокруг одного или нескольких значений и т. д. Из изображений Ниже вы можете лучше понять, как это выглядит.

Как видите, точки данных на первом изображении расположены близко друг к другу. Поскольку все значения расположены где-то между 5 и 25, значения точек данных не сильно различаются. Второе изображение, однако, иллюстрирует точки данных с довольно большим разбросом . На этот раз значения варьируются примерно от 5 до 95, где вариация выше, поскольку точки данных принимают различные значения.

Третье изображение — еще один пример высокой степени изменчивости. Однако в этом сценарии большинство значений расположены около 10. Это основная причина, по которой показатели центральной тенденции часто указываются с 9.0055 меры изменчивости , потому что они дают более полную картину того, как данные распределяются вокруг каких центральных значений либо вместо визуализаций, как в приведенных выше, но чаще в дополнение к визуализациям.

Напомним, что статистика также использует различные формулы и методы, когда речь идет о выборках и совокупностях. В то время как совокупность содержит все элементы, которые мы хотим изучить, например, все школы в стране, выборка содержит часть этих элементов, например, сто школ в стране. Поскольку у нас редко когда-либо появляется возможность измерить целые популяции, «истинные» измерения редко известны и называются параметрами. С другой стороны, поскольку показатели, рассчитанные по выборке, не являются истинными показателями генеральной совокупности, а скорее оценок этих истинных цифр, они называются статистикой.

Что такое дисперсия?

Дисперсия переменной или набора данных определяется как разброс их точек данных. Это похоже на то, что мы обсуждали ранее, потому что дисперсию можно рассматривать как уровень вариации в наборе данных. Формулу для дисперсии выборки и генеральной совокупности можно увидеть в таблице ниже.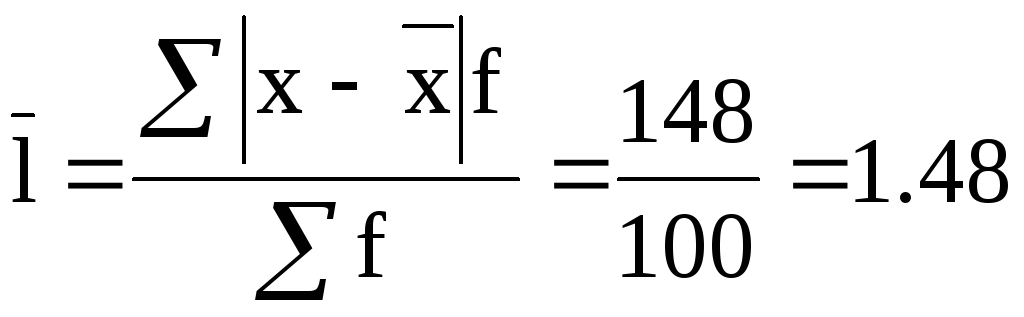

Выборочная дисперсия	Population Variance

We’ll break down step by step what this means. Поскольку вариация является попыткой измерить изменчивость набора данных, она сравнивает каждую точку данных с средним значением всех точек данных, а затем делит на размер выборки минус 1, чтобы получить среднее значение.

Объяснение	Шаг
1. Сначала вы вычисляете среднее, чтобы иметь основу для сравнения всех значений.
2. Затем вы вычисляете разницу между каждой точкой данных и средним значением. Подумайте об этом — если эта разница велика для большинства данных, это означает, что многие точки расположены далеко от центра и наоборот
3. Эта разница возводится в квадрат для работы с отрицательными значениями. Если бы мы оставили эти отрицательные значения, сумма разницы была бы недооценена. Например, предположим, что у вас есть среднее значение 50 и точка данных 4, что даст разностное значение -46. Здесь важна величина этой разницы, а не положительная она или отрицательная. Однако, если мы сохраняем отрицательный знак, это искусственно занижает сумму. Возведение в квадрат — это простой способ работы с отрицательными числами в целом.
4. Берется сумма этих квадратов разностей. Это отражает общую величину различий от среднего значения.
5. Деление на размер выборки является естественным способом оценки величины дисперсии на точку данных, подобно нахождению среднего значения. Однако мы делим на -, чтобы получить несмещенную выборочную дисперсию (операция вычитания 1 известна как поправка Бесселя)

Следуя этим шагам, мы используем приведенную ниже таблицу данных в качестве примера, чтобы найти дисперсию.

Observation	Value
1	45	45 — 41.2 =3.8	14.4
2	32	32 — 41,2 = -9,2	84.6
3	29	29 — 41.2 =-12.2	148.8
4	56	56 — 41.2 =14.8	219
5	44	44 — 41.2 =2.8	7.8
			474.8

Where the mean is calculated as,

   

And where,

   

   

Что такое стандартное отклонение?

Как вы могли заметить, хотя понять дисперсию может быть легко, ее интерпретация может оказаться непростой задачей. Хотя полезно думать о вариации как о среднем расстоянии каждой точки данных от среднего, вы должны помнить, что вы не только делите сумму разностей на n — 1, а не только на n, но также и то, что сумма разностей равна в квадратных единицах. Это означает, что дисперсия также выражается в квадратах. В буквальном переводе из приведенного выше примера дисперсия сигнализирует о приблизительной квадратичной разнице в 118,7 на точку данных.

Вот почему во многих случаях стандартное отклонение является предпочтительной мерой изменчивости. Напомним, что формула стандартного отклонения — это просто квадратный корень из дисперсии. Это связано с тем, что единицы переходят от единиц в квадрате к исходным единицам данных. Формулу стандартного отклонения можно найти ниже.

Стандартное отклонение выборки	Стандартное отклонение населения

Проблема 1

Найдите стандартное отклонение следующего набора данных.

Observation	Value
1	173
2	149
3	165
4	157
5	164

Решение Задача 1

Чтобы найти стандартное отклонение, необходимо сначала найти среднее значение.

   

Следующий шаг — вычесть среднее значение из всех значений в наборе данных, возвести в квадрат эти вычтенные значения, а затем сложить их все вместе. После этого просто подставьте его в формулу стандартного отклонения .

   

Проблема 2

Используя следующую информацию, найдите дисперсию.

Measure	Value
Mean	179
Sample Size	3 000
SD	9

Решение Задача 2

Напомним, что стандартное отклонение — это просто квадратный корень из дисперсии.