свойства, формулы включений и исключений, примеры
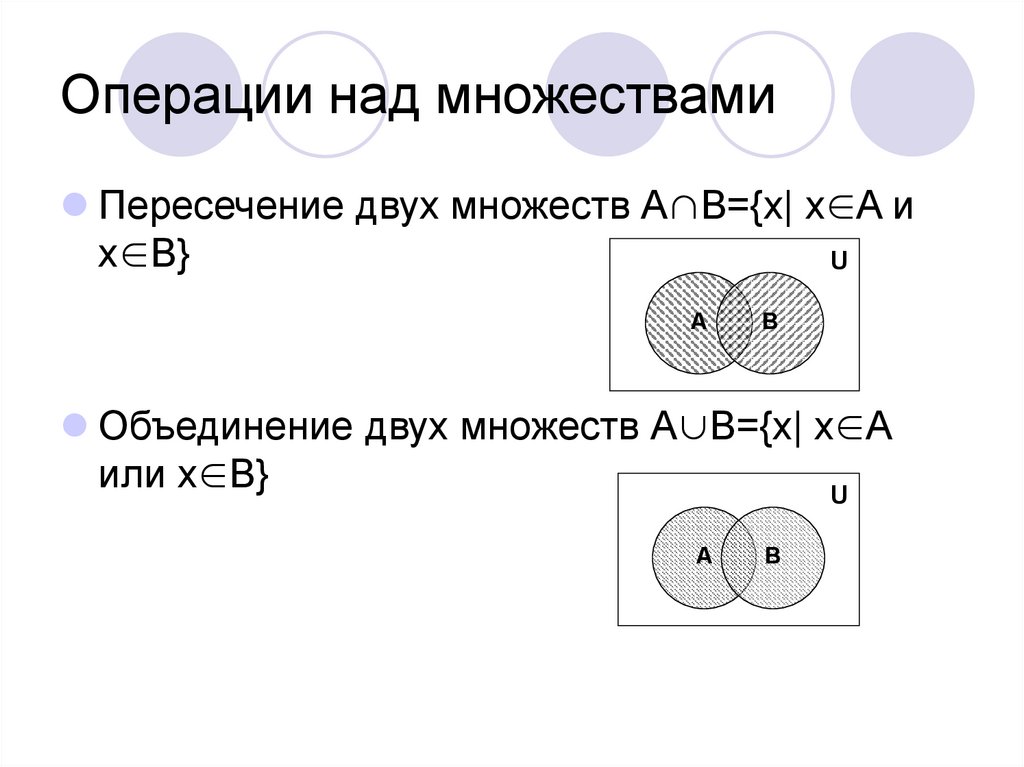
- Пересечение множеств
- Объединение множеств
- Универсум и отрицание
- Свойства операций пересечения и объединения
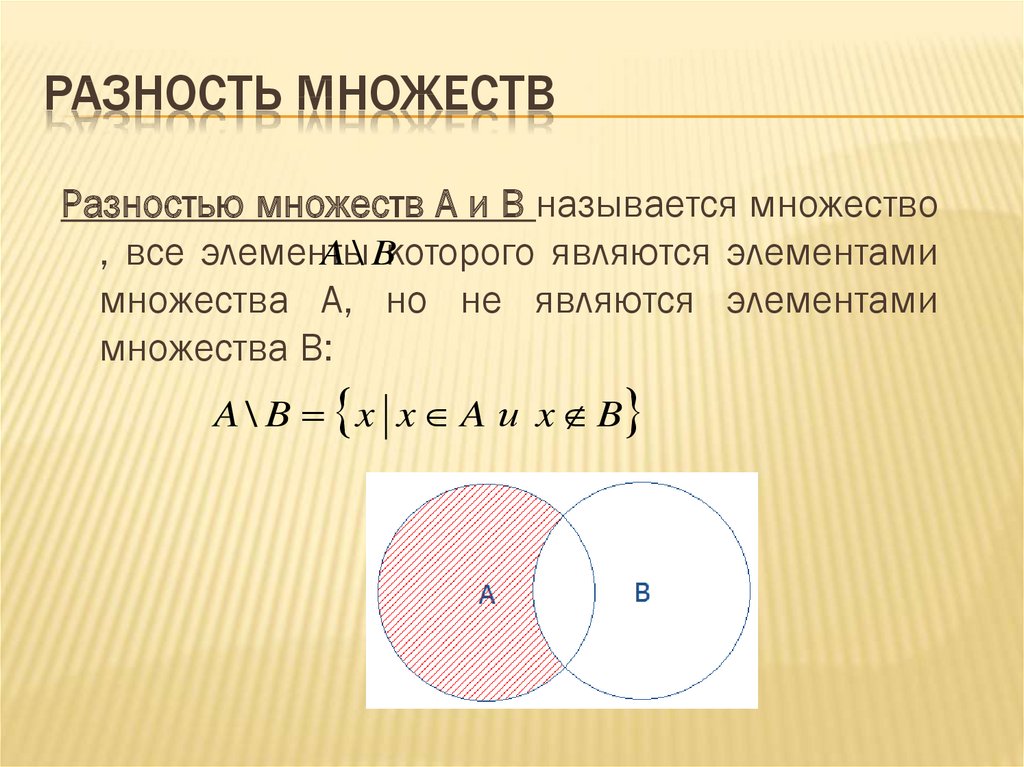
- Разность множеств
- Формулы включений и исключений
- Примеры
Пересечение множеств
Если множества не пересекаются, то $A \cap B = \varnothing $ — пустое множество в пересечении. Если $B \subseteq A$ — подмножество, то $A \cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A \cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A \cap B$ = {f|f-квадрат}.
Если A = $\{n|n⋮3, n \in \Bbb N \}$ — натуральные числа, кратные 3, B = $\{n|n⋮5, n \in \Bbb N \}$ — натуральные числа, кратные 5, то $A \cap B = {n|n⋮15, n \in \Bbb N}$ — натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A \cap B = \varnothing$. 2-4 = 0, x \in \Bbb R\}, B = \{x|x+3 = 2, x \in \Bbb R \}, то A \cup$ B = {-2;-1;2}
2-4 = 0, x \in \Bbb R\}, B = \{x|x+3 = 2, x \in \Bbb R \}, то A \cup$ B = {-2;-1;2}
Если $A = \{n│n \in \Bbb Z \}$- все целые числа, $B = \{x|x = \frac{a}{b}, a \in \Bbb Z, b \in \Bbb N \}$ — все дроби, то $A \cup B = \{x│x \in \Bbb Q\}$ — множество рациональных чисел. Заметим, что в данном случае $A \subset B$.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
Примеры универсумов:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Читается «не A».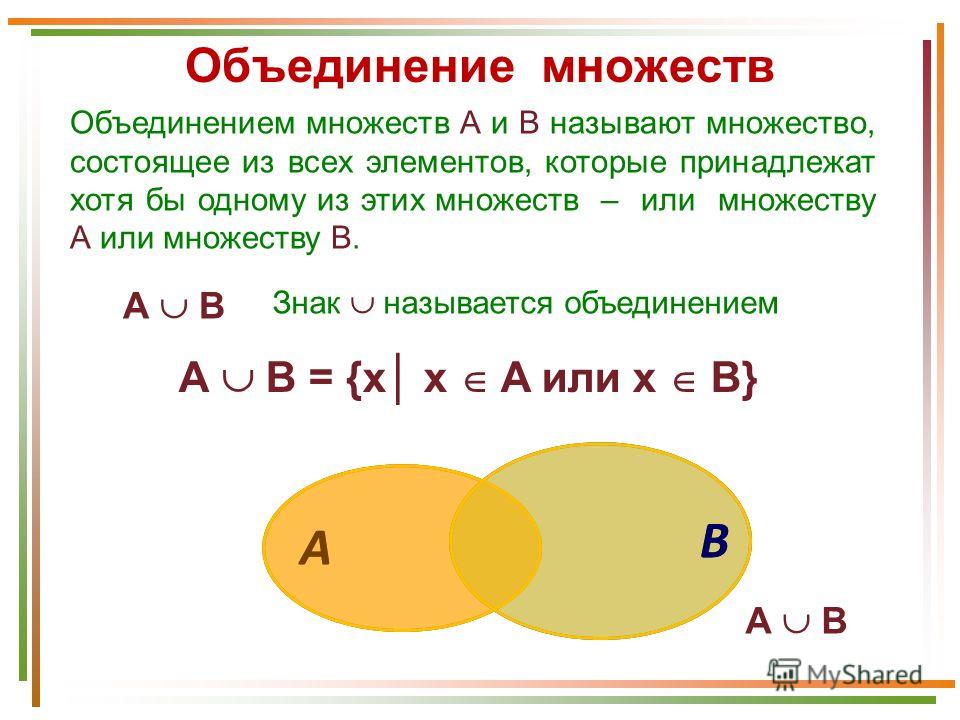
У отрицания есть любопытное свойство: $\bar{\bar{Α}} = Α $(два раза «нет» — это «да»).
Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $\bar{A} = \{1;2;6;7\}$
Если U = $\{x|x \in \Bbb R\}$ — все действительные числа, A = $\{x|x \gt 0, x \in \Bbb R \}$ — все положительные действительные числа, то $ \bar{A} = \{x|x \le 0, x \in \Bbb R\}$.
Свойства операций пересечения и объединения
Пересечение
Объединение
Коммутативность
$A \cap B = B \cap A$
$ A \cup B = B \cup A $
Ассоциативность
$(A \cap B) \cap C = A \cap (B \cap C)$
$ (A \cup B) \cup C = A \cup ( B \cup C) $
Дистрибутивность
$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$
$ (A \cap B) \cup C = (A \cup C) \cap (B \cup C) $
Идемпотентность
$A \cap A = A$
$ A \cup A = 0 $
Взаимодействие с отрицанием, пустым множеством и универсумом
$A \cap \bar{A} = \varnothing $
$A \cap U = A$
$A \cap \varnothing = \varnothing$
$A \cup \bar{A} = U $
$A \cup U = U$
$A \cup \varnothing = A$
Законы де Моргана
$ \overline{(A \cap B)} = \bar{A} \cup \bar{B} $
$ \overline{(A \cup B)} = \bar{A} \cap \bar{B} $
Закон поглощения
$ (A \cup B) \cap A = A $
$ (A \cap B) \cup A = A $
Разность множеств
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Получается, что отрицание – частный случай разности: $ \bar{A} = \{x|x \in \Bbb U, x \notin A \} $= U\A
«Не A» — это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A \cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A \cup B)$?
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A \cup B) = n(A)+ n(B)-n(A \cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.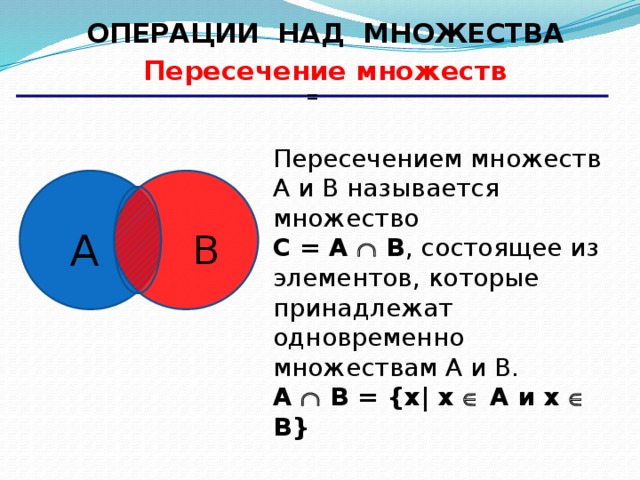 е. отнять сумму $(n(A \cap B)+n(A \cap C)+n(B \cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A \cap B \cap C)$; значит, его нужно «вернуть».
е. отнять сумму $(n(A \cap B)+n(A \cap C)+n(B \cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A \cap B \cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A \cup B \cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A \cap B)+n(A \cap C)+n(B \cap C) )+n(A \cap B \cap C) $$
Примеры
Пример 1. Найдите пересечение данных множеств:
а) A = {0;5;8;10},
B = {3;6;8;9}
$A \cap B$ = {8}
$б) A = \{x|x \lt 3, x \in \Bbb R\}, $
$ B = \{x|x \gt 1, x \in \Bbb R\} $
$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb R\}$ — отрезок
$в) A = \{x|x \lt 3, x \in \Bbb R\}, $
$ B = \{x|x \gt 1, x \in \Bbb N\} $
$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb N \} или A \cap B = \{2\}$ — одна точка
г) A = {f|f-правильный многоугольник},
B = {f|f-четырехугольник}
$A \cap B = \{f|f-квадрат\}$
Пример 2. Найдите объединение данных множеств:
а) A = {0;5;8;10}, B = {3;6;8;9}
$A \cup B$ = {0;3;5;6;8;9;10}
б) A = {1;2}, B = {1;2;3;4}
$A \subset B$ – строгое подмножество
$A \cup B $ = B = {1;2;3;4}
$в) A = \{x|x \lt 1, x \in \Bbb R\}, B = \{x|x \gt 1,x \in \Bbb R\} $
$A \cup B = \{x|x \neq 1, x \in \Bbb R \}$
$г) A = \{n│n⋮3, n \in \Bbb Z\}, B = \{n|n⋮9,n \in \Bbb N\} $
$B \subset A$ — строгое подмножество
$ A \cup B = A = \{n│n⋮3, n \in \Bbb Z\} $
Пример 3. Найдите отрицание данного множества на данном универсуме:
Найдите отрицание данного множества на данном универсуме:
а) U = {1;2;3;4;5}, A = {2;3}
$ \bar{A} = {1;4;5}$
б) U = $\{x│x \in \Bbb Q \}$, A = $\{ \frac{4}{5}, \frac{7}{8} \}$
$ \bar{A} = \{x|x \neq \frac{4}{5}, x \neq \frac{7}{8}, x \in \Bbb Q\} $
$в) U = \{x│x \in \Bbb R\}, A = \{x|x \ge 2, x \in \Bbb R\} $
$\bar{A} = \{x|x \lt 2, x \in \Bbb R\}$
г) U = { 0;1}, A = { 0}
$ \bar{A} = {1}$
Пример 4. Найдите обе разности данных множеств:
а) A = {0;1;2;3;4}, B = {2;4}
A\B = {0;1;3}, $B\A = \{∅\}$
б) A = {0;1;3}, B = {2;4;6}
A\B = {0;1;3}, B\A = {2;4;6}
$в) A = \{x|x \gt 1, x \in \Bbb R\}, $
$ B = \{x|x \lt 3, x \in \Bbb R\} $
A\B $ = \{x|x \ge 3, x \in \Bbb R\}$
B\A $ = \{x|x \le 1,x \in \Bbb R\} $
$ г*) A = \{(x,y)|x \gt 0, x \in \Bbb R, y \in \Bbb R\} $
$ B = \{(x,y)|x \le 5, x \in \Bbb R, y \in \Bbb R\} $
A\B $ = \{(x,y)|x \gt 5, x \in \Bbb R, y \in \Bbb R\} $
B\A $ = \{(x,y)|x \le 0, x \in \Bbb R, y \in \Bbb R\} $
Пример 5. Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?
Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?
n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42
$ n(A \cap B) = 8, n(B \cap C) = 5, n(A \cap C) = 10 $
$n(A \cap B \cap C) = 3$
Всего программистов:
$ n(A \cup B \cup C) = n(A)+n(B)+n(C)- $
$ (n(A \cap B)+n(B \cap C)+n(A \cap C) )+n(A \cap B \cap C) $
$n(A \cup B \cup C) = 28+30+42-(8+5+10)+3 = 100-23+3 = 80$
Число не умеющих программировать:
$n(U)-n(A \cup B \cup C) = 100-80 = 20$
Ответ: 20 человек
Пересечение и объединение множеств 9 класс онлайн-подготовка на Ростелеком Лицей
Повторение знаний о множестве
Пересечение и объединение множеств – операции над множествами.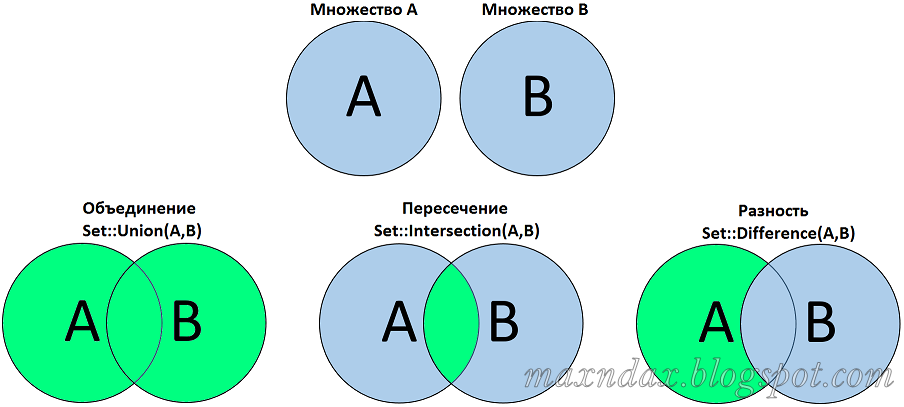
Пример на применение объединения и пересечения множеств
Пример: В классе 19 учеников: 10 девочек, 9 мальчиков.
10 девочек – это множество .
9 мальчиков – это множество .
Класс из 19 учеников – это множество С, которое объединяет два множества.
Пусть в классе 5 отличников – это множество D.
Из них 2 мальчика – это множество E.
Из какие элементов состоит множество Е?
Мальчики входят в множества В, так как 2 мальчика – отличники, они входят в множество D.
Рис. 1. Пересечение двух множеств
Множество Е есть пересечение двух множеств В и D(рис. 1).
Определение понятия объединение множеств
Определение: объединением множеств А и В называется новое множество, состоящее из тех и только тех элементов, которые входят хотя бы в одно из множеств А или В (рис. 3).
3).
Рис. 2. Множества
Рис. 3. Объединение множеств
– знак объединения.
Множество состоит из всех элементов , которые входят или в множество , или в множество . Это можно записать следующим образом:
Пример № 1 на применение определения объединение множеств
Дано множество = и .
Найти объединение множеств .
Решение:
Пример № 2 на объединение бесконечных множеств
Дано множество и .
Найти объединение множеств .
Решение:
Имеем совокупность неравенств:
Пример № 3. Решение квадратного неравенства
Решить квадратное неравенство .
Решение:
Рассмотрим функцию .
Найдём корни функции .
По теореме Виета: .
Имеем объединение двух множеств .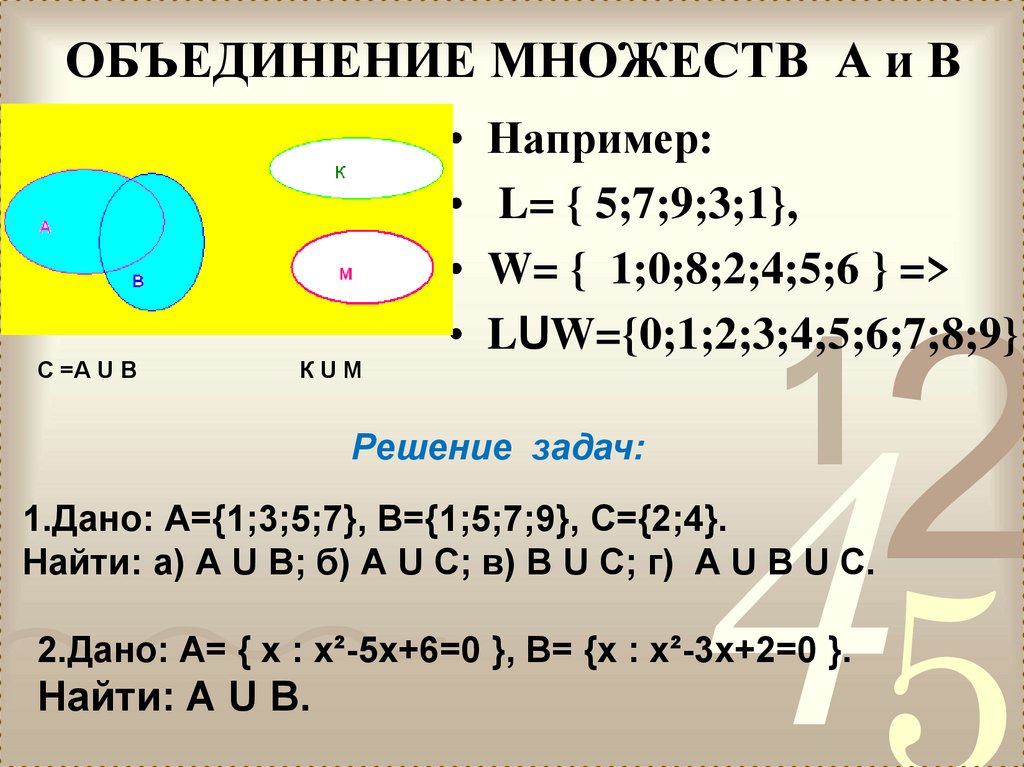
Схематически изобразим график функции:
при или .
Ответ:.
Определение понятия пересечение множеств
Пересечение множеств
Пересечением множеств Aи B называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество А, и в множество В.
– знак пересечения
Рис. 4а. Пересечение множеств
– пересечение множеств на рис. 4а
Рис. 4б. Пересечения множеств нет
На рис. 4б множества не пересекаются, их пересечение – пустое множество
Пример № 4 на применение определения пересечения множеств
Даны множества и . Найти пересечение множеств .
Решение
По определению пересечения, решением будут те элементы, которые одновременно входят в оба множества:
– пересечение множеств.
Сравним с объединением:
C= – объединение множеств.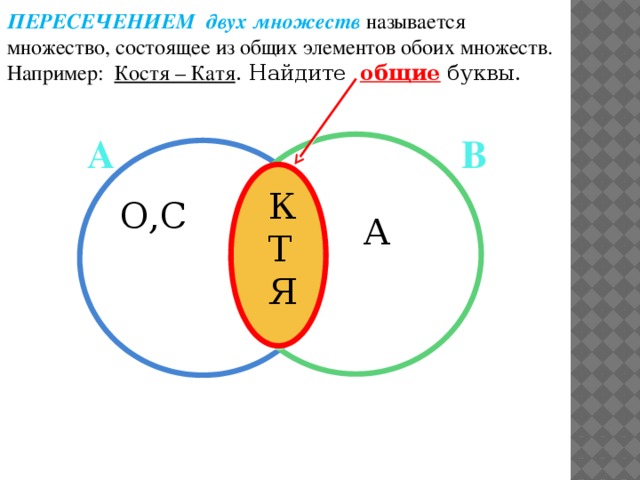
Пример № 5 на пересечение бесконечных множеств
Найти пересечение бесконечных множеств
Решение
Нужно найти такие х, которые принадлежат пересечению :
Нужно решить систему неравенств. На оси изображаем множества и находим их пересечение
Ответ:
.
Сравним с объединением множеств:
Пример № 6. Решение системы неравенств
Решить систему неравенств
Решение:
Рассмотрим ось х:
Ответ:
Пересечением множеств будет:
Итог
Мы рассмотрели объединение и пересечение множеств; решили типовые задачи.
Список литературы
- В.А. Ильин, В.А. Садовничий, Бл.Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред.
 А. Н. Тихонова. – 3-е изд., перераб. и доп. – М.: Проспект, 2006. – Т. 1. – С. 66. – 672 с.
А. Н. Тихонова. – 3-е изд., перераб. и доп. – М.: Проспект, 2006. – Т. 1. – С. 66. – 672 с. - А.Г. Мордкович, П.В. Семёнов. Алгебра. 9 класс. В 2-х частях. Часть 1. Учебник. (ФГОС) 16-е издание, исправленное. – М.: Мнемозина, 2013.
- А.Г. Мордкович, П.В. Семёнов. Алгебра. 9 класс. В 2-х частях. Часть 1. Задачник. 16-е издание, исправленное. – М.: Мнемозина, 2013.
- А.Г. Мордкович, П.В. Семёнов. Алгебра. 9 класс. Методическое пособие для учителя. – М.: Мнемозина, 2013.
- А.Г. Мордкович, Н.П. Николаев. Алгебра. 9 класс. В 2-х частях. Часть 1 – учебник. (ФГОС) Учебник для классов с углублённым изучением математики. – М.: Мнемозина, 2014.
- А.Г. Мордкович. Преподавание алгебры. Методическое пособие для учителя. 8–9 класс. – М.: Мнемозина, 2014.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Raal100.narod.ru (Источник).
- Men-c.com (Источник).

- Википедия (Источник).
Домашнее задание
- Даны множества А = {3,5, 0, 11, 12, 19}, В = {2,4, 8, 12, 18,0}. Найдите множества AU В.
- Пусть A – это множество натуральных чисел, делящихся на 2, а В – множество натуральных чисел, делящихся на 4. Какой вывод можно сделать относительно данных множеств?
- Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом – 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
|
Середина урока Диалог/ Групповая работа
4 мин
Групповая работа
Межпредметная связь
2 мин Индивидуальная работа 5 мин
Групповая работа 8–10 мин |
Дифференциация по классификации – смешанная группа. Деление учащихся на группы по принципу «1, 2, 3, 4, 5» (в каждой группе по одному сильному учащемуся (эксперту). Повторение пройденной темы на прошлом уроке. На столах лежат карточки, с вопросами, взятыми из ресурса BilimLand (эксперты организуют диалог, слушают участников групп, проверяют записанные ответы, дополняют при необходимости).
Метод: «Светофор»
Просмотр обучающего курса Bilim Media Group по теме «Объединение и пересечение множеств» Учащиеся конспектируют необходимую информацию.
Задание на закрепление материала:
Обратная связь: — К примеру, мы свами часто используем такую фразу, как: «логично», «не логично». Основу логических суждений как раз составляют множества с определенными элементами. В старших классах на уроках информатики вы часто будете выстраивать логические цепочки при составлении алгоритмов, написании кода.
В данную викторину интегрированы тестовые вопросы с образовательного ресурса BilimLand. Объединение: А ∪ В =
— Метод: «Светофор»
Класс разделен на четыре команды по 5 учащихся. Предлагается набор разноуровневых заданий по данной теме, за решение которых можно получить 18 баллов. На обсуждение и предварительное распределение заданий в группе отводится 1 минута. Если команда выполнила все задания первой, то для этой команды на интерактивную доску выводятся ответы для самопроверки. В конце игры подводятся итоги.
Цели:
Уровень А (по 3 балла за верно решенное задание)
— находят объединение и пересечение множеств;
Метод «Светофор»: |
карточки
сигнальные карточки светофор
планшет, с установленной программой для флипчарта
4 слайд
Карточки с заданиями, планшеты
5 слайд (решение) |
страница 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Похожие работы
|
Множества. Пересечение множеств. Объединение множеств — страница №1/1 Московский Педагогический Колледж №6 на тему: «Множества. Пересечение множеств. Объединение множеств» В 10«E» классе школы №591 Студента 5-ого курса 58 группы Чернышова Игоря Утверждаю: Учитель Роденкова Е. Методист Михасёв В.Г._________ Оценка за урок_________ 2008 год Тема урока: «Множества. Пересечение множеств. Объединение множеств» Цель урока: научить учеников выполнять операции пересечения и объединения множеств. Задачи:
Оборудование: доска.
|
Урок по теме «Пересечение и объединение множеств». 6-й класс
Тип урока: изучение нового материала.
Цели:
- формирование знаний о пересечении и объединении множеств;
- развитие умений и нахождение числа элементов пересечения и объединения множеств, выявлять закономерность, обобщать и делать выводы, воспитание ответственного отношения к учебе.
Ход урока
1. Организационный момент.
2. Повторение изученного по теме «Множества».
Вопросы для учащихся:
- Что такое множество?
- Что такое элементы множества?
- Какое множество конечно и бесконечно?
- Какое множество называется пустым?
3. Изучение нового материала «Пересечение множеств».
Учитель. Рассмотрим следующие два множества: М – множество всех точек круга, N – множество точек прямой, пересекающей круг. Каждый видит, что пересечение круга с прямой – это отрезок; обозначим его концы буквами А и В. Задумаемся: каким свойством обладают точки этого отрезка по отношению к множествам М и N? Ответ ясен: точки отрезка АВ – это в точности те точки, которые принадлежат и множеству М, и множеству N. Так что множество всех точек отрезка АВ естественно назвать пересечением множеств М и N.
Задумаемся: каким свойством обладают точки этого отрезка по отношению к множествам М и N? Ответ ясен: точки отрезка АВ – это в точности те точки, которые принадлежат и множеству М, и множеству N. Так что множество всех точек отрезка АВ естественно назвать пересечением множеств М и N.
Точно так же можно определить пересечение любых двух множеств М и N. Пересечением множеств М и N называется множество, состоящее из всех элементов, принадлежащих каждому из множеств М и N. Пересечение множеств М и N обозначают М ∩ N. Читают: «пересечение М и N» или «М пересечение N». Знак ∩ называется знаком пересечения.
Обсудим несколько примеров.
Пример 1. М – множество всех учениц какой-то школы, N – множество всех учащихся данного класса этой школы. Тогда М ∩ N – это множество всех девочек из данного класса.
Тогда М ∩ N – это множество всех девочек из данного класса.
Пример 2. М – множество всех квартир на 1-м этаже в каком-то доме, N – множество всех квартир в данном подъезде этого дома. Тогда М ∩ N – это множество всех квартир на 1-м этаже в данном подъезде.
Пересечение множеств точек двух фигур на плоскости легче представить, если нарисовать эти фигуры. Сделаем это, например, для двух кругов. Множество всех точек первого круга обозначим М, второго – N. Для пересечения М ∩ Nмогут быть три варианта; они изображены на рисунке.
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то легко записать их пересечение.
Примеры:
Пересечение можно образовывать не только для двух множеств, но и для любого их числа. Определяется это точно так же, как и для двух множеств: пересечением данных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств. Пересечение множеств М, N и Р обозначается М ∩N ∩ Р.
Пересечение множеств М, N и Р обозначается М ∩N ∩ Р.
Вопрос для учащихся:
Что обозначает запись Р ∩ Q ∩ R ∩ S? Какому множеству равно это пересечение, если
4. Первичное закрепление понятия пересечения множеств.
Вопросы:
- Что такое пересечение двух множеств; нескольких множеств?
- Что значит, что два множества не пересекаются? Приведите 2-3 примера непересекающихся множеств.
- Какое множество обозначается знаком ?
Практические задания:
1. Для каждой пары множеств М и Nзапишите их пересечение:
N – множество всех неправильных дробей.
2. Для каждой пары множеств М и N укажите их пересечение:
- М – множество всех нечетных чисел, N – множество всех натуральных чисел, делящихся на 4;
- М – множество всех правильных дробей, N – множество всех десятичных дробей;
- М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 5.

3. Дан многоугольник. Каждую его сторону будем рассматривать как множество всех точек, принадлежащих этой стороне. Для каждой пары сторон многоугольника укажите множество, равное пересечению этих двух сторон, если многоугольник – это:
а) треугольник АВС;
б) прямоугольник KLMN.
4. Рассмотрите три множества {1, 2}, {2, 3}, и {3, 1}. Убедитесь, что их пересечение пусто, а пересечение любых двух из этих множеств не пусто.
5. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
- Запишите всевозможные попарные пересечения этих множеств. Имеются ли среди них равные?
- Запишите всевозможные пересечения троек этих множеств. Имеются ли среди них равные?
- Запишите пересечение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
5. Изучение нового материала «Объединение множеств».
Изучение нового материала «Объединение множеств».
Учитель. Объединением множеств М и N называется множество всех элементов, принадлежащих хотя бы одному из множеств М и N.
Объединение множеств М и N обозначают М N. Читают: «объединение М и N» или «М объединение N». Знак называется знаком объединения.
Разберем несколько примеров. Обдумайте каждый из них.
Пример 1. М – множество всех учеников данного класса, получивших на сегодняшний день пятерку по какому-нибудь предмету, N – множество всех учеников того же класса, получивших в этот день четверку по какому-нибудь предмету. Тогда М N – это множество всех учеников данного класса, получивших за сегодняшний день повышенные отметки.
Пример 2. М – множество всех правильных дробей, N – множество всех неправильных дробей. Тогда М N – это множество всех обыкновенных дробей.
Тогда М N – это множество всех обыкновенных дробей.
Пример 3. М – множество всех букв слова КОШКА, N – множество всех букв слова МЫШКА. Тогда М N = {А, К, М, О, Ш, Ы}.
Задание для учащихся: Приведите сами какой-нибудь пример объединения двух множеств.
Учитель. Как и пересечение, объединение можно образовать не только для двух множеств, но и для любого их числа: объединением данных множеств называется множество, состоящее…
Закончите определение. Догадайтесь, как записать объединение трех множеств М, N и Р.
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то, как и для пересечения, легко записать их объединения.
Для любых множеств М и N можно образовать их пересечение М ∩ N и объединение М N. Это похоже на то, что происходит при действиях над числами: для любых двух чисел m и n можно образовать их произведение m n и сумму m+n. Так получаются действия, которые назвали умножением и сложением. Поэтому образование пересечения и образование объединения можно назвать действиями над множествами.
Так получаются действия, которые назвали умножением и сложением. Поэтому образование пересечения и образование объединения можно назвать действиями над множествами.
Выполняются ли те же законы для пересечения и объединения множеств? Давайте рассуждать. Начнем с переместительного закона.
Повторим, что такое пересечение двух множеств: множество М ∩ N состоит из всех элементов, принадлежащих каждому из множеств М и N, а множество N ∩М состоит из всех элементов, принадлежащих каждому из множеств Nи М. Но сказать «каждому из множеств М и N» или «каждому из множеств N и М» — значит сказать одно и то же: ведь ясно, что неважно, в каком порядке перечислять здесь множества. Значит, множества М ∩N и N ∩М состоят из одних и тех же элементов, т.е.
М ∩ N = N ∩М.
Данное равенство и означает, что переместительный закон для пересечения верен.
Чтобы проверить сочетательный закон, надо убедиться, что для любых трех множеств М, N и Р выполняется равенство
М ∩(N ∩Р)= (М ∩N) ∩Р
Легко понять, что в левой и правой частях этого равенства записаны множества, состоящие из всех элементов, принадлежащих каждому из множеств М, N и Р, т.е. состоящие из одних и тех же элементов. Это и означает, что требуемое равенство выполняется.
6. Первичное закрепление изученного понятия объединения множеств.
Вопросы:
- Что такое объединение двух множеств; нескольких множеств?
- О выполнении каких законов для действий пересечения и объединения множеств идет речь в объяснительном тексте этого параграфа?
- Каким множеством – конечным или бесконечным – будет объединение: а) двух конечных множеств; б) двух бесконечных множеств; в) конечного и бесконечного множеств?
Практические задания:
1. Для каждой пары множеств М и N запишите их объединение:
Для каждой пары множеств М и N запишите их объединение:
2. Для каждой пары множеств М и N укажите их объединение:
- М – множество всех нечетных чисел, N – множество всех четных чисел;
- М – множество всех квадратов на плоскости, N – множество всех прямоугольников на той же плоскости, четырехугольников;
- М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 15.
3. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
- Запишите всевозможные попарные объединения этих множеств. Имеются ли среди них равные?
- Запишите всевозможные объединения троек этих множеств. Имеются ли среди них равные?
- Запишите объединение всех этих множеств.
 Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
7. Изучение нового – вывод правила подсчета числа элементов объединения и пересечения множеств.
Учитель. Чтобы вывести правило давайте разберем конкретный пример. Пусть М = {Вася, Валя, Вера, Игорь}, т.е. m=4;
N = {Валя, Гриша, Игорь}, т.е. n=3.
Запишем объединение этих множеств:
М N = {Вася, Валя, Вера, Гриша, Игорь}.
В множестве МN пять элементов, а m+n=4+3=7. Вот мы и видим, что в МN элементов меньше чем 7.
Почему так получилось? Да потому, что в данном примере можно указать учеников, которые в этот день получили и пятерку, и четверку. Другими словами здесь пересечение М ∩N не пусто: М ∩ N = {Валя, Игорь}. Но в объединении-то МN каждый элемент пересечения М ∩N присутствует (и подсчитывается) только один раз, а не два раза.
Давайте-ка изобразим ситуацию нашего примера на рисунке.
Если бы подсчитали здесь сумму m+n (т.е. 4+3), то каждый элемент пересечения (в данном примере Валя и Игорь, т.е. 2 элемента) оказался бы подсчитанным дважды. Значит, чтобы узнать число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов пересечения. В данном примере получаем 4+3-2=5.
Данная задача была решена с помощью рисунка, этот способ называется «Круги Эйлера». Леонард Эйлер – швейцарский математик, который в 18 веке работал в Российской академии наук и сделал много открытий для нашей науки.
Итак, если мы возьмем сумму m+n, то в ней элементы пересечения М ∩N будут сосчитаны дважды. Значит, чтобы определить число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов из М ∩N, т.е. число р. Получим такую формулу: q=m+n-p.
Сформулируем правило для нахождения числа элементов объединения множеств:
Чтобы найти число элементов объединения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их пересечения.
Сформулируем правило для нахождения числа элементов пересечения множеств:
Чтобы найти число элементов пересечения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их объединения.
8. Первичное закрепление изученного.
Практические задания (устно):
1. Вычислите число элементов в объединении множеств М и N, если:
- М содержит 10 элементов, N – 15 элементов, а М ∩N – 7 элементов;
- М содержит 27 элементов, N – 18 элементов, а М ∩N – 13 элементов;
- М содержит 45 элементов, N – 57 элементов, а М ∩N – 1 элемент.

2. Вычислите число элементов в пересечении множеств М и N, если:
- М содержит 10 элементов, N – 15 элементов, а М ∩N – 17 элементов;
- М содержит 27 элементов, N – 18 элементов, а М ∩ N – 45 элементов;
- М содержит 45 элементов, N – 57 элементов, а М ∩N – 100 элементов.
Решение задач с помощью кругов Эйлера:
№1. В классе 28 учеников. Каждый из них начертил у себя в тетради один из двух четырехугольников – прямоугольник или ромб. При проверке прямоугольников оказалось 17, а ромбов – 15. Как такое могло случиться?
№2. В осенние каникулы 12 учеников класса участвовали в междугородных экскурсиях в Москву и Санкт-Петербург, при этом 8 из них посетили Санкт-Петербург, а 6 – Москву. Сколько из этих учеников побывало и в Москве, и в Санкт-Петербурге?
Задание на дом:
№1. Найдите пересечение множеств учителей, которые вели уроки в вашем классе: а) вчера и сегодня; б) вчера и позавчера. Оказалось ли какое-то из этих двух пересечений пустым?
Найдите пересечение множеств учителей, которые вели уроки в вашем классе: а) вчера и сегодня; б) вчера и позавчера. Оказалось ли какое-то из этих двух пересечений пустым?
№2. Вася, рассматривая свой дневник погоды, обнаружил, что в сентябре 17 раз отмечен дождь и 19 раз – сильный ветер. При этом дней, когда одновременно шел дождь и дул сильный ветер, оказалось 7. Был ли хоть один день, когда не было ни дождя, ни сильного ветра?
Тема 1.1.5 Разбиение на части — Мегаобучалка
Под классификацией в науке понимают логическую операцию, состоящую в разбиении всего множества по каким – либо свойствам на подмножества, при этом должны выполняться условия:
1) ни одно из подмножеств не пусто;
2) подмножества попарно не пересекаются;
3) объединение всех подмножеств совпадает с самим множеством.
Классификацию можно выполнить:
1) путем указания признака (класс имеющих и не имеющих указанный признак).
Если на множестве Х задано одно свойство, то это множество разобъется на 2 класса (I – объекты, которые обладают эти свойством , II – не обладают).
Например, множество натуральных чисел по признаку быть двузначным числом, или быть кратным 3.
Классификация – это наведение порядка в множестве (все «вещи» раскладываются по «полочкам»). Ни один предмет не может находиться одновременно на 2-х полках, кроме того, все до одного предмета должны быть убраны).
Упражнения
1. Даны два множества: X = {2, 4, 6} и Y = {0, 2, 4, 6, 8}.
Верно ли что:
а) множества X и Y пересекаются;
б) множество X является подмножеством множества Y;
в) множество Р = {4, 0, 6, 8, 2} равно множеству У?
2. Из множества К = {216, 546, 153, 171, 234} выпишите
числа, которые:
а) делятся на 3; б) делятся на 9;
в) не делятся на 4; г) не делятся на 5.
Есть ли среди полученных подмножеств такое, которое равно множеству К!
3. Изобразите при помощи кругов Эйлера отношения между множествами Си D, если:
а) С — множество двузначных чисел,
D = {3,43, 34, 56, 103};
б) С — множество двузначных чисел,
D — множество четных натуральных чисел;
в) С — множество двузначных чисел,
D — множество трехзначных чисел;
г) С — множество двузначных чисел,
D — множество натуральных чисел, не меньших 10.
4. Какое из данных множеств является подмножеством другого:
а) А — множество натуральных чисел, кратных 2,
В — множество натуральных чисел, кратных 6,
С — множество натуральных чисел, кратных 3.
б) А — множество треугольников,
В — множество прямоугольных треугольников, С- множество остроугольных треугольников.
Пересечение множеств:
1) Пусть даны два множества: А = {2, 4, 6, 8} и В = {5, 6, 7, 8, 9}. Образуем множество С, в которое включим общие элементы множеств А и В, т.е. С = {6, 8}. Так полученное множество С называют пересечением множествА и В.
Определение. Пересечением множеств А иВ называется множество, содержащее те и только те элементы, которые принадлежат множеству А и множеству В. Пересечение множеств А и В обозначают А В. Таким образом, по определению, А В = {х|х А и х В}. Если изобразить множества А и В при помощи кругов Эйлера, то пересечением данных множеств является заштрихованная область .
Если изобразить множества А и В при помощи кругов Эйлера, то пересечением данных множеств является заштрихованная область .
В том случае, когда множества А и В не. имеют общих элементов, говорят, что их пересечение пусто и пишут: А В = 0.
2) Если множества заданы характеристическими свойствами своих элементов?
Найдем, например, пересечение множества А — четных натуральных чисел и множества В- двузначных чисел. Характеристическое свойство элементов множества А — «быть четным натуральным числом», а характеристическое свойство элементов множества В- «быть двузначным числом». Тогда, согласно определению, элементы пересечения данных множеств должны обладать свойством «быть четными натуральными и двузначными числами». Таким образом, множество А В состоит из четных двузначных чисел (союз «и» в данном случае можно опустить). Полученное множество не пусто. Например, 24 А В, поскольку число 24 четное и двузначное.
Упражнения
1. Найдите пересечение множеств А и В, если:
a)A = {a,b,c,d,e,f},B={b,e,f,k}
б) А = {26,39,5,58, 17,81}, В= {17,26,58}.
в) А = {26,39,5,58, 17, 81}, В= {17, 26, 58, 5, 39, 81}.
2.Из каких элементов состоит пересечение множества букв в слове «математика» и множества букв в слове «геометрия»?
3.М- множество однозначных чисел, Р- множество нечетных натуральных чисел. Из каких чисел состоит пересечение данных множеств? Содержатся ли в нем числа -7 и 9?
4.Начертите два треугольника так, чтобы их пересечением: а) был треугольник; б) был отрезок; в) была точка.
Объединение множеств
1) Пусть даны два множества: А = {2, 4, 6, 8} и В = {5, 6, 7, 8, 9}. Образуем множество D, в которое включим элементы, принадлежащие хотя бы одному из данных множеств, т.е. множеству А или множеству В: D = {2, 4, 6, 8, 5, 7, 9}. Так полученное множество D называют объединением множеств А и В.
Так полученное множество D называют объединением множеств А и В.
Определение. Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают А В. Таким образом, по определению, А и В = {х \ х А или х В}.
РИСУНОК:
Если множества заданы характеристическими свойствами их элементов, то надо использовать союз « или».
2)Найдем, например, объединение множества А — «быть четным натуральным числом», а свойство элементов множества В- «быть двузначным числом», то в объединение данных множеств войдут числа, характеристическое свойство которых- «быть четным натуральным или двузначным числом». Тогда Д=А В
Пример: 8 А В , 36 А В
3)Рассмотрим теперь случай: А В=А,т.е. В А , характеристическое свойство элементов множества А и В будет таким, как и свойство элементов множества А.
Упражнения
1. Найдите объединение множеств А и В, если:
а) А = {а, Ъ, с, d, e,f), В = {Ь, e,f, k).
6)А = {26,39,5,58, 17, 81}, В= {17,26,58}.
в)А = {26,39,5,58, 17, 81}, В= {17,26,58,5,39,81}.
2. Из каких элементов состоит объединение множества букв м слове «математика» и множества букв в слове «геометрия»?
3. М — множество однозначных чисел, Р- множество нечетных натуральных чисел. Из каких чисел состоит объединение данных множеств? Содержатся ли в нем числа -7 и 9?
4. Используя координатную прямую, найдите объединение множеств решений неравенств, в которых х- действительное число:
а) х > -2 и х > 0; . в) х 5 и х < -7,5;
б) х > -3,7 и х 4; г) -2 <х < 4 и х -1;
д)-7 х 5 и -6 х 2.
8. Начертите две фигуры, принадлежащие объединению множеств С и D, если:
а) С-множество ромбов,
D — множество прямоугольников;
б) С — множество равнобедренных треугольников,
D — множество прямоугольных треугольников.
Пересечение множеств — формула, примеры
Пересечение множеств для двух заданных множеств — это множество, содержащее все элементы, общие для обоих множеств. Символом пересечения множеств является «∩». Для любых двух множеств A и B пересечение A ∩ B (читается как пересечение A B) перечисляет все элементы, присутствующие в обоих множествах, и являются общие элементы A и B.
Например, если Set A = {1,2,3,4,5} и Set B = {3,4,6,8}, A ∩ B = {3,4} Разберемся подробнее о свойствах пересечения множеств, дополнении пересечения множества, с помощью примеров, часто задаваемых вопросов.
| 1. | Что такое пересечение множеств? |
| 2. | Дополнение пересечения множеств |
| 3. | Пересечение множеств Диаграмма Венна |
| 4. | Свойства пересечения множеств |
| 5. | Пересечение наборов Примеры |
6. | Часто задаваемые вопросы о пересечении наборов |
Что такое пересечение множеств?
Пересечение множеств – множество элементов, общих для обоих заданных множеств. В теории множеств для любых двух множеств A и B пересечение определяется как множество всех элементов множества A, которые также присутствуют в множестве B. Мы используем символ «∩», который обозначает «пересечение». Например, давайте представим студентов, которые любят мороженое на десерт, Брэндона, Софи, Люка и Джесс. Это набор А. Студенты, которые любят пирожные на десерт, — это Рон, Софи, Миа и Люк. Это набор B. Студенты, которые любят и мороженое, и пирожные, — это Софи и Люк. Это представляется как A ∩ B.
Кардинальное число
Кардинальное число набора — это общее количество элементов, присутствующих в наборе. Например, если Set A = {1,2,3,4}, то кардинальное число (представленное как n (A)) = 4. Рассмотрим два множества A и B. A = {2, 4, 5, 6, 10,11,14, 21}, B = {1, 2, 3, 5, 7, 8,11,12,13} и A ∩ B = {2, 5, 11}, и кардинальное число пересечения A B представлен n(A ∩ B) = 3.
n(A ∩ B)= n(A) + n(B) — n(A ∪ B)
Непересекающиеся множества
Два множества A и B, не имеющие общих элементов, называются непересекающимися, если A ∩ B = ϕ, то A и B называются непересекающимися множествами. Пример: если А = { 2, 3, 5, 9} и B = {1, 4, 6, 12}, A ∩ B = { 2, 3, 5, 9} ∩ {1, 4, 6, 12} = ϕ. Поэтому множества A и B называются непересекающимися множествами.
Подмножества
Если множество A — это множество натуральных чисел от 1 до 10, а множество B — это множество нечетных чисел от 1 до 10, то B — это подмножество A. Пересечение множеств — это подмножество каждого множества. образуя пересечение, (A ∩ B) ⊂ A и (A ∩ B) ⊂ B.
Например, A = {3, 4, 2, 2 6, 7, 8, 9, 10}, B = {2, 4, 7, 12, 14}, A ∩ B = {2, 4, 7}. Таким образом, A ∩ B — подмножество A, а A ∩ B — подмножество B.
Дополнение пересечения наборов
Множество всех элементов в универсальном множестве, но не в A ∩ B, является дополнением пересечения множеств. Если X = {1, 2, 3, 4, 5}, Y = {2,4,6,8,10} и U = {1,2,3,4,5,6,7,8,9 ,10}, то X ∩ Y = {2,4} и (X ∩ Y)’ = {1,3, 5,6,7,8,9,10}. Дополнение пересечения множеств обозначается как (X∩Y)´.
Если X = {1, 2, 3, 4, 5}, Y = {2,4,6,8,10} и U = {1,2,3,4,5,6,7,8,9 ,10}, то X ∩ Y = {2,4} и (X ∩ Y)’ = {1,3, 5,6,7,8,9,10}. Дополнение пересечения множеств обозначается как (X∩Y)´.
Пересечение множеств Диаграмма Венна
Пересечение множеств можно легко понять с помощью диаграмм Венна. Диаграммы Венна используют круги для представления каждого набора. Перекрывающиеся круги означают, что между двумя или более наборами существует некоторая связь и что они имеют общие элементы. А круги, которые не перекрываются, не имеют общих элементов. На следующей диаграмме показано пересечение множеств с помощью диаграммы Венна. Здесь Set A = {1,2,3,4,5} и Set B = {3,4,6,8}. Следовательно, A ∩ B = {3,4}
Свойства пересечения множеств
Пересечение множеств обладает свойствами, аналогичными свойствам чисел. К свойствам пересечения множеств относятся коммутативный закон, ассоциативный закон, закон нулевого множества и универсального множества и закон идемпотента. В следующей таблице перечислены свойства пересечения множеств.
В следующей таблице перечислены свойства пересечения множеств.
| Наименование собственности/закона | Правило |
| Коммунативное право | А ∩ В = В ∩ А |
| Ассоциативное право | (А ∩ В) ∩ С = А ∩ (В ∩ С) |
| Закон ϕ и U | ϕ ∩ A = ϕ , U ∩ A= A |
| Закон идемпотента | (А ∩ (В ∪ С) = (А ∩ В) ∪ (А ∩ С) (А ∪ (В ∩ С) = (А ∪ В) ∩ (А ∪ С) |
Важные примечания:
- (A ∩ B) — множество всех элементов, общих для обоих множеств A и B.
- Если A ∩ B = ϕ, то A и B называются непересекающимися множествами.
- n(A ∩ B) = n(A) + n(B) — n(A ∪ B)
Темы, связанные с пересечением множеств
Ознакомьтесь с некоторыми интересными статьями, связанными с пересечением множеств.
- Набор нотаций Builder
- Операции с множествами
- Универсальный набор
- Диаграммы Венна
Часто задаваемые вопросы о пересечении наборов
Что такое пересечение множеств?
Для любых двух множеств A и B пересечение множеств представляется как A ∩ B и определяется как группа элементов, присутствующих в множестве A, которые также присутствуют в множестве B. Это известно как пересечение множеств. .
Что означает A ∩ B в математике?
A ∩ B означает общие элементы, принадлежащие как множеству A, так и множеству B. В математике ∩ — это символ, обозначающий пересечение множеств.
Что такое объединение и пересечение множеств?
Для любых двух множеств A и B объединение множеств, обозначаемое A U B, представляет собой множество всех элементов, присутствующих в множестве A, и множество элементов, присутствующих в множестве B, или и то, и другое. Пересечение двух множеств – это множество элементов, общих как для множества A, так и для множества B.
Что означает ∩ в теории вероятности?
Если есть два события A и B, то ∩ обозначает вероятность пересечения событий A и B.
Какая формула пересечения двух множеств?
Пересечение двух или более данных множеств — это множество элементов, общих для каждого из данных множеств. Пересечение множеств обозначается символом ‘∩’. В случае независимых событий мы обычно используем правило умножения P(A ∩ B) = P(A)P(B).
Какова мощность пересечения множеств A и B?
Общее количество элементов в наборе называется количественным числом набора. Для двух конечных множеств A и B n(A ∩ B) = n(A) + n(B) – n(A ∪ B).
Является ли A ∩ B равным B ∩ A?
В соответствии с коммутативным свойством пересечения множеств порядок операционных множеств не влияет на результирующее множество, и поэтому A ∩ B равно B ∩ A. Например, для множеств P = {a, b, c, d, e} и Q = {a, e, i}, A ∩ B = {a,e} и B ∩ A = {a.e}. Таким образом, A ∩ B = B ∩ A.
Что такое символ пересечения множеств?
Математический символ, используемый для обозначения пересечения множеств, — ‘ ∩’.
Что такое дополнение пересечения множеств?
Дополнением множества A ∩ B называется множество элементов, являющихся элементами универсального множества U, но не принадлежащих множеству A ∩ B. Другими словами, дополнением пересечения данных множеств является объединение множеств исключая их пересечение. Оно представляется как (A ∩ B)´.
Объединение и пересечение двух множеств
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4738
- Ларри Грин
- Общественный колледж Лейк-Тахо
Результаты обучения
- Найдите объединение двух наборов.
- Найдите пересечение двух множеств.

- Объединить союзы пересечений и дополнений.
Все классы статистики включают вопросы о вероятностях объединения и пересечения множеств. В английском языке мы используем слова «Или» и «И» для описания этих понятий. Например, «Найдите вероятность того, что учащийся посещает урок математики или науки». Это выражает союз двух множеств словами. «Какова вероятность того, что медсестра имеет степень бакалавра и более пяти лет опыта работы в больнице». Это выражение пересечения двух множеств. В этом разделе мы научимся расшифровывать эти типы предложений и узнаем о значении союзов и пересечений.
Элемент находится в объединении двух наборов, если он находится в первом наборе, втором наборе или в обоих. Символ, который мы используем для объединения, — это \(\cup\). Слово, которое вы часто будете видеть, обозначающее союз, — это «или».
Пример \(\PageIndex{1}\): Объединение двух наборов
Пусть:
\[A=\left\{2,5,7,8\right\} \nonumber\]
и
\[B=\lbrace1,4,5,7,9\rbrace \nonumber \]
Найти \(A\cup B\)
Решение
Включим в объединение каждое число из A или находится в B:
\[A\cup B=\left\{1,2,4,5,7,8,9\right\} \nonumber \]
Пример \(\PageIndex{2}\): Союз двух наборы
Рассмотрим следующее предложение: «Найдите вероятность того, что в доме менее 6 окон или дюжина окон». Запишите это в обозначении множества как объединение двух множеств, а затем запишите это объединение.
Запишите это в обозначении множества как объединение двух множеств, а затем запишите это объединение.
Решение
Во-первых, пусть A будет набором количества окон, который представляет «менее 6 окон». В этот набор входят все числа от 0 до 5:
\[A=\left\{0,1,2,3,4,5\right\} \nonumber \]
Далее, пусть B будет набором количества окон, который представляет «имеет дюжину окон «. Это просто множество, содержащее единственное число 12:
\[B=\left\{12\right\} \nonumber \]
Теперь мы можем найти объединение этих двух множеств:
\[A\ cup B=\left\{0,1,2,3,4,5,12\right\} \nonumber \]
Элемент находится на пересечении двух множеств, если он находится в первом множестве и находится в второй набор. Символ, который мы используем для пересечения, — \(\cap\). Слово, которое вы часто будете видеть, которое указывает на пересечение, это «и».
Пример \(\PageIndex{3}\): пересечение двух наборов
Пусть:
\[A=\left\{3,4,5,8,9,10,11,12\right\} \nonumber \]
и
\[B=\lbrace5,6,7,8,9\rbrace \nonumber \]
Найти \(A\cap B\).
Решение
Мы включаем в пересечение только те числа, которые находятся как в A, так и в B:
\[A\cap B=\left\{5,8,9\right\} \nonnumber \]
Пример \(\PageIndex{4}\): пересечение двух множеств
Рассмотрим следующее предложение: «Найдите вероятность того, что количество единиц, которые сдает учащийся, больше 12 единиц и меньше 18 единиц». Предполагая, что учащиеся берут только целое число единиц, запишите это в системе обозначений как пересечение двух множеств, а затем запишите это пересечение.
Решение
Во-первых, пусть A будет набором номеров единиц, который представляет «более 12 единиц». В этот набор входят все числа, начинающиеся с 13 и продолжающиеся до бесконечности: 9.0005
\[A=\left\{13,\:14,\:15,\:…\right\} \nonumber \]
Далее, пусть B будет набором количества единиц, представляющих » менее 18 единиц». Это набор, содержащий числа от 1 до 17:
\[B=\left\{1,\:2,\:3,\:. ..,\:17\right\} \nonumber \]
..,\:17\right\} \nonumber \]
Теперь мы можем найти пересечение этих двух множеств:
\[A\cap B=\left\{13,\:14,\:15,\:16,\:17\right\} \nonumber \ ]
Одной из самых больших проблем в статистике является расшифровка предложения и преобразование его в символы. Это может быть особенно сложно, когда есть предложение, в котором нет слов «союз», «пересечение» или «дополнение», но оно неявно относится к этим словам. Лучший способ овладеть этим навыком — практиковаться, практиковаться и еще раз практиковаться.
Пример \(\PageIndex{5}\)
Рассмотрим следующее предложение: «Если вы бросаете шестигранный кубик, найдите вероятность того, что он не четный и не выпадет 3». Запишите это в системе обозначений.
Решение
Во-первых, пусть A будет набором четных чисел, а B будет набором, содержащим только 3. Мы можем написать:
\[A=\left\{2,4,6\right\} ,\:\:\:B\:=\:\left\{3\right\} \nonumber \]
Далее, поскольку мы хотим «не четное», нам нужно рассмотреть дополнение A: 9c=\:\left\{1,3,5\right\}\cap\left\{1,2,4,5,6\right\}=\left\{1,5\right\} \nonumber \]
Пример \(\PageIndex{6}\)
Рассмотрим следующее предложение: «Если вы случайно выбираете человека, найдите вероятность того, что этот человек старше 8 лет или одновременно моложе 6 лет и не моложе 3″. Запишите это в системе обозначений.
Запишите это в системе обозначений.
Решение
Во-первых, пусть A — множество людей старше 8 лет, B — множество людей младше 6 лет, а C — множество людей младше 3 лет. Мы можем написать: 9c\right)=\:\left\{x\mid x>8\right\}\cup\left\{x\mid3\le x<6\right\} \nonumber \]
Самый четкий способ отображения этот союз находится на числовой прямой. Числовая строка ниже отображает ответ:
Упражнение
Предположим, что мы выбрали человека наугад и заинтересованы в нахождении вероятности того, что месяц рождения этого человека наступил после июля, а не после сентября. Запишите это событие, используя набор обозначений.
- Пример: найти пересечение множества и дополнения с помощью диаграммы Венна
- Пересечение и дополнения наборов
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Ларри Грин
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Метки
- ПЕРЕКРЕСТКИ
- союзов
Объединение, пересечение и дополнение | Математика для гуманитарных наук
Результаты обучения
- Описать принадлежность множеств, включая пустое множество, используя соответствующие обозначения, и решить, являются ли данные элементы элементами, и определить мощность данного множества.

- Опишите отношения между множествами относительно членства, равенства, подмножества и правильного подмножества, используя соответствующие обозначения.
- Выполните операции объединения, пересечения, дополнения и разности над множествами, используя соответствующие обозначения.
- Уметь рисовать и интерпретировать диаграммы Венна для отношений множеств и операций, а также использовать диаграммы Венна для решения задач.
- Распознавать, когда теория множеств применима к ситуациям из реальной жизни, решать проблемы из реальной жизни и сообщать о реальных проблемах и решениях другим.
Обычно наборы взаимодействуют. Например, вы с новым соседом по комнате решаете устроить домашнюю вечеринку и приглашаете друзей. На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.
Объединение, пересечение и дополнение
объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах). The union is notated A ⋃ B. More formally, x ∊ A ⋃ B if x ∈ A or x ∈ B (or both)
The union is notated A ⋃ B. More formally, x ∊ A ⋃ B if x ∈ A or x ∈ B (or both)
The пересечение двух наборов содержит только те элементы, которые есть в обоих наборах. Пересечение обозначено как A ⋂ B. Более формально, x ∈ A ⋂ B , если x ∈ A и x ∈ B.
комплемент из набора A содержит все, что является , а не в подборе A . Дополнение обозначается как A’ , или A c , или иногда ~ A .
Универсальный набор — это набор, содержащий все интересующие нас элементы. Это должно определяться контекстом.
Дополнение относится к универсальному набору, поэтому A c содержит все элементы универсального набора, которых нет в A .
Пример
- Если бы мы обсуждали поиск книг, универсальный набор мог бы включать все книги в библиотеке.
- Если бы мы группировали ваших друзей на Facebook, универсальным набором были бы все ваши друзья на Facebook.
- Если вы работали с наборами чисел, универсальный набор мог бы состоять из всех целых чисел, всех целых чисел или всех вещественных чисел
Пример
Предположим, что универсальный набор равен U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то A c = {3, 5, 5, 6, 7, 8, 9}.
Попробуйте
Пример
Рассмотрим наборы:
A = {красный, зеленый, синий}
B = {красный, желтый, оранжевый} {красный, желтый, оранжевый}
C 905 желтый, зеленый, синий, фиолетовый}
Найдите следующее:
- Найти А ⋃ В
- Найти А ⋂ В
- Найти A c ⋂ C
Показать решение
Попробуй
Обратите внимание, что в приведенном выше примере было бы сложно просто попросить A c , поскольку все, от цвета фуксии до щенков и арахисового масла, входит в комплект набора. По этой причине дополнения обычно используются только с пересечениями или когда у нас есть универсальный набор.
По этой причине дополнения обычно используются только с пересечениями или когда у нас есть универсальный набор.
Как мы видели ранее с выражением A c ⋂ C , операции над множествами можно группировать вместе. Символы группировки можно использовать так же, как и с арифметикой — для принудительного порядка операций.
Пример
Предположим, H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик}, и W = {утка, кролик, олень, лягушка, мышь}
- Найти ( H ⋂ F ) ⋃ Вт
- Найти H ⋂ ( F ⋃ W )
- найти ( H ⋂ F ) c ⋂ W
Показать решение
Чтобы визуализировать взаимодействие множеств, Джон Венн в 1880 году решил использовать перекрывающиеся круги, опираясь на аналогичную идею, использованную Леонардом Эйлером в 18 веке. Эти иллюстрации теперь называются Диаграммы Венна .
Эти иллюстрации теперь называются Диаграммы Венна .
Диаграмма Венна
Диаграмма Венна представляет каждое множество в виде окружности, обычно нарисованной внутри прямоугольника, представляющего универсальное множество. Перекрывающиеся области обозначают элементы, общие для обоих наборов.
Основные диаграммы Венна могут иллюстрировать взаимодействие двух или трех множеств.
Example
Create Venn diagrams to illustrate A ⋃ B , A ⋂ B , and Ac ⋂ B
A ⋃ B contains all elements in либо комплект.
Показать решение
Пример
Используйте диаграмму Венна для иллюстрации ( H ⋂ F ) c ⋂ W
Показать решение
Пример
Создайте выражение для представления выделенной части показанной диаграммы Венна.
Показать решение
Попробуйте
Создайте выражение, представляющее выделенную часть показанной диаграммы Венна.
Объединение и пересечение множеств
Объединение двух множеств P и Q представлено как P ∪ Q. Это множество всех различных элементов, включенных в P или Q. Символ, используемый для обозначения объединение множеств есть ∪.
Пересечение двух множеств P и Q представлено как P ∩ Q. Это множество всех различных элементов, которые входят как в P, так и в Q. Символ, используемый для обозначения пересечения множеств, ∩ . Можно сказать, что пересечение двух заданных множеств, т. е. P и Q, — это множество, включающее все элементы, общие как для P, так и для Q.
Пример:
Если P = { 1,3,5,7,9} и Q = { 2,3,5,7}
Что такое P ∪ Q и P ∩ Q
Решение:
P ∪ Q = { 1,2,3,5,7,9}
P ∩ Q = { 3,5,7}
Отличным способом изучения объединения и пересечения множеств является с помощью диаграмм Венна. Диаграмма Венна объединения и пересечения обсуждается ниже.
Диаграмма Венна объединения и пересечения обсуждается ниже.
Объединение и пересечение Диаграмма Венна
Диаграмма Венна представляет собой диаграмму, которая представляет отношения между конечной группой множеств. Если у нас есть два или более наборов, мы можем построить диаграмму Венна, чтобы представить отношения между этими наборами, а также мощность наборов. Диаграммы Венна полезны для представления взаимосвязей в статистике, вероятности и во многих других областях.
Диаграммы Венна специально используются при работе с множествами, поскольку они дают нам визуальную информацию о вовлеченных отношениях.
Чтобы изучить объединение и пересечение с помощью диаграммы Венна, мы представим множества кружками, как показано ниже:
(Изображение будет загружено в ближайшее время)
Теперь мы поместим значения в соответствующие места.
(изображение будет загружено в ближайшее время)
Объединение множества представляет собой любую область, включающую элементы A или B
(Изображение будет загружено в ближайшее время)
Пересечением множеств является любая область, включающая элементы A и B.
(Изображение будет загружено в ближайшее время)
Объединение двух множеств P и Q эквивалентно множеству элементов, входящих в множество P, в множество Q или в оба множества P и Q. Эта операция может быть представлена в виде
P ∪ Q = { a : a ∈ P или a ∈ Q}
Давайте разберемся с объединением множества на примере, скажем, установите P {1,3,} и установите Q = {1,2,4}, тогда
P ∪ Q = { 1,2,3,4,5}
Диаграмма Венна объединения множеств
Рассмотрим универсальное множество U такое, что A и B являются подмножествами этого универсального множества. Объединение двух множеств А и В определяется как множество всех элементов, входящих в множество А, или множество В, или и то, и другое. Символ «∪» используется для обозначения объединения двух множеств.
Объединение двух множеств А и В определяется как множество всех элементов, входящих в множество А, или множество В, или и то, и другое. Символ «∪» используется для обозначения объединения двух множеств.
(изображение будет загружено в ближайшее время)
На диаграмме Венна, приведенной выше, желтая часть обозначает объединение обоих множеств A и B. Следовательно, объединение двух множеств A и B представлено множество C, которое также рассматривается как подмножество универсального множества U такое, что множество C включает в себя все те элементы, которые находятся либо в множестве A, либо в множестве B, либо в обоих A и B, т. е. A ∪ B = { x : x ∈ A или x ∈ B }.
Пересечение множеств
Пересечение двух множеств A и B, являющихся подмножествами универсального множества U, представляет собой множество, включающее все те элементы, которые являются общими для A и B.
Оно представлено символ ‘∩’. Все те элементы, которые входят в множество A и B, обозначают пересечение A и B. Следовательно, мы можем сказать, что A ∩ B = { x : x ∈ A и x ∈ B }.
Для n множеств, т. е. A₁, A₂, A₃,…. An, где все эти множества являются подмножеством универсального множества U, пересечение — это множество всех элементов, общих для всех этих n множеств.
Периодически представляя это, заштрихованная часть на приведенной ниже диаграмме Венна обозначает пересечение двух множеств A и B.
(изображение будет загружено в ближайшее время) Y — два множества, то пересечение двух множеств представлено
X ∩ Y = n( X) + n(Y) — n( X ∩ Y)
Где n(X) — кардинальное число множества X. , n(Y) — кардинальное число множества Y, n( X ,Y ) — кардинальное число объединения множества X и Y.
Чтобы ясно понять концепцию пересечения двух множеств, рассмотрим пример.
Если набор X = {4,6,8,10,12}, набор Y = {3,6,9,12,15,18} и набор Z = {1,2,3,4,5,6 ,7,8,9,10}. Найдите пересечение
1. Набор X и Y
2. Набор Y и Z
3. Набор A и C
Решение:
Набор всех элементов, которые являются общими для обоих наборов X и Y, равен { 6, 12}
Множество всех элементов, общих для множества Y и Z, равно {3,6,9}
Множество всех элементов, общих для множества X и Z, равно {4,6,8,10}
Кардинальное число множества
Число различных элементов, включенных в конечное множество, называется его кардинальное число множества. Кардинальное число множеств представляется как n(A) и читается как «количество элементов множества».
Например,
Множество X = { 2,4,5,9,15 } состоит из 5 элементов
Следовательно, кардинальное число множества X = 5. Следовательно, оно представляется как n(x) = 5.
Следовательно, оно представляется как n(x) = 5.
Разница между Союзом и пересечением набора
Союз | Интерсал из | . Сетей | . элементов, входящих либо в множество X, либо в множество Y, либо в оба множества X и Y. | Пересечение двух множеств X и Y определяется как множество элементов, принадлежащих обоим множествам X и Y. |
Символ ∪ используется для обозначения объединения двух наборов. | Символ ∩ используется для обозначения пересечения двух множеств. |
Союз набора соответствует логическому или | . Пересечение набора соответствует логическому и |
. Это переосмысляет идентичные значения из набора | 111 . |
Пример: если X = { 1,2,3} и Y = { 2, 3, 4}, то X ∪ Y = { 1,2,3,4} | Пример: если X = { 1,2,3} и Y = { 2, 3, 4}, тогда X ∩ Y = { 2,3} |
Примеры объединения и пересечения
1. Если X = { Число, кратное 3 от 1 до 20}, и Y = (Нечетные натуральные числа до 14}. Определите пересечение двух заданных множеств X и Y.
Решение:
X = { кратное 3 от 1 до 20}
Следовательно, X = {3,6,9,12,15,18}
Y = {четные натуральные числа до 15}
Следовательно, Y = {2,4,6,8,10,12,14 }
Следовательно, пересечение X и Y является наибольшим множеством, включающим только те элементы, которые являются общими для обоих заданных множеств X и Y. = {1,3,7,5} и Q = {3,7,8,9}. Найдите объединение двух множеств P и Q.
Решение:
P ∪ Q = { 1,3,5,7,8,9}
В объединении двух множеств нет повторяющихся элементов. Общие элементы, т.е. 3 и 7, рассматриваются только один раз.
Общие элементы, т.е. 3 и 7, рассматриваются только один раз.
Объединение и пересечение множеств Практические задачи по количественным числам
1. Найдите объединение и пересечение двух множеств P и Q Где множество P = { -29, -45, -10, -30, -3, -39 , 24} и установить Q = {-46, 21,-8}. Каково кардинальное число P, Q, их объединение и пересечение?
Решение:
Союз = {-29, — 45, -10, — 30, — 3, — 39, 24, — 46, 21,- 8}
Пересечение {}
Кардинальное число P = Число элементов в P = 7
Кардинальное число Q= Количество элементов в Q = 3
Кардинальное число объединения двух наборов = Общее количество элементов в обоих наборах = 10
Кардинальное число пересечения двух наборов= Количество элементов в их пересечении = 0 (нулевой набор).
2. Всего в XI классе учится 200 учеников. Среди них 120 студентов изучают естественные науки, 50 студентов математику и 30 студентов изучают как естественные науки, так и математику. Найдите количество учащихся, которые
Найдите количество учащихся, которые
Наука исследования, но не математика
ИССЛЕДОВАНИЯ Математика, но не наука
- . Пусть x представляет собой набор студентов, изучающих естественные науки, а набор Y представляет студентов, изучающих математику.
Следовательно,
n(U) = 200
N(X) = 120
N(Y) = 50
N ( X ∩ Y) = 30
Диаграмма Венна обозначает количество студентов, изучающих как естественные науки, так и математику.
i. Количество студентов, изучающих естествознание, но не математику
Здесь требуется найти разность множеств X и Y. — Y) = n(X) — n(X ∩ Y)
n( X -Y) = 120 -30
= 90
Следовательно, количество студентов, изучающих естествознание, но не математику, равно 90.

ii. Количество студентов, изучающих математику, но не естественные науки.
Здесь требуется найти разность множеств Y и X. — n(X ∩ Y)
n(X -Y) = 50 -30
= 20
Следовательно, количество студентов, изучающих математику, но не естествознание, равно 20.
iii. Количество студентов, изучающих естественные науки или математику
n( X ∪ Y) = n(X) + n(Y) — (X ∩ Y)
n ( X ∪Y) = 120 + 50 — 30 = 140
Следовательно, количество студентов, изучающих естествознание или математику которые могут быть математическими, как функции, числа, а могут и не быть математическими. Использование наборов должно быть старше, чем использование самих чисел. Количество животных в стаде можно сосчитать с помощью камней в мешке без подсчета реальных членов. Это понятие простирается до бесконечности. Например, когда мы рассматриваем множество, содержащее целые числа, то целые числа от 1 до 100 конечны, но если мы рассматриваем все множество, то оно будет бесконечным.
 Наборы представлены множеством членов, заключенных в квадратные скобки. Когда в наборе нет элементов, он называется нулевым или пустым набором. Бесконечные множества представлены формулой, которая дает элементы при использовании для элементов множества.
Наборы представлены множеством членов, заключенных в квадратные скобки. Когда в наборе нет элементов, он называется нулевым или пустым набором. Бесконечные множества представлены формулой, которая дает элементы при использовании для элементов множества.Функция объединения двух наборов содержит все элементы или объекты, присутствующие в двух наборах или в одном из двух наборов. Он представлен ⋃. Функция пересечения двух наборов — это когда присутствуют все элементы, присутствующие в обоих наборах. Он представлен как ⋂.
Функция дополнения пересечения не содержит всего, что присутствует на множестве. С другой стороны, универсальный набор содержит все необходимые нам элементы в наборе. Можно сказать, что дополнительное множество относится к универсальному множеству.
Объединение и пересечение наборов
Наборы — это четко определенный набор данных/объектов. Данные/объекты принадлежат к одной и той же группе, но все данные отличаются друг от друга.
 Например, если слово «приложение» должно быть помещено в множество, оно будет выглядеть примерно так: множество A = {a, p, l, i, c, t, o, n}, буквы, которые повторяются в слова, такие как «p», «a», «i», пишутся только один раз, так как они представляют собой повторяющиеся одни и те же элементы.
Например, если слово «приложение» должно быть помещено в множество, оно будет выглядеть примерно так: множество A = {a, p, l, i, c, t, o, n}, буквы, которые повторяются в слова, такие как «p», «a», «i», пишутся только один раз, так как они представляют собой повторяющиеся одни и те же элементы.Типы наборов
Существуют различные виды наборов в зависимости от того, какой тип элемента и сколько элементов присутствует в наборе, может быть 5 элементов или 1 элемент, или конечное количество элементов, но слишком много, или ни одного элемента в все в комплекте. Давайте посмотрим на типы,
- Одиночный набор ⇢ Набор, состоящий только из одного элемента. Например, A= {1}, B= {e}, C= {a: a∈N, 57}.
- Нулевой набор ⇢ Нулевые наборы — это наборы, в которых нет ни одного элемента. Нулевые наборы также известны как пустой набор или пустой набор. Нулевые наборы существуют для объяснения определенных параметров, например, если в вопросе предлагается поместить в набор числа, которые больше 8 и меньше 6, существуют ли какие-либо числа? Нет.
 Поэтому в таком случае используется Null set ⇢ {}/∅. Нулевой набор также важен, поскольку он является частью каждого набора, подмножеством каждого набора.
Поэтому в таком случае используется Null set ⇢ {}/∅. Нулевой набор также важен, поскольку он является частью каждого набора, подмножеством каждого набора. - Конечный набор ⇢ Конечные наборы имеют конечное число элементов, количество элементов не играет важной роли, пока в наборе присутствует конечное число элементов, набор будет называться
- a Конечный набор. Например, A = {a, e, i, o, u}, B = {1, 3, 5, 7, 9….95, 97, 99}.
- Бесконечный набор ⇢ Бесконечные наборы — это наборы, в которых присутствует бесконечное количество элементов, в наборе может быть бесконечное количество элементов. Например, если кто-то спрашивает о натуральных числах и требуется составить их набор, то натуральные числа начинаются с 1, но потом они бесконечны, доходят до бесконечности, следовательно, элементы множества всех -натуральные числа будут бесконечностью. Бесконечные множества обозначаются точками в конце последнего записанного элемента, чтобы показать, что он доходит до бесконечности.
 Например, A= {2, 4, 6, 8, 10, 12….}
Например, A= {2, 4, 6, 8, 10, 12….}
Операции с множествами
В теории множеств очень часто встречаются два или более двух множеств, демонстрирующих тот или иной тип отношения. Наборы могут иметь общие данные, что, скорее всего, произойдет, иногда наборы не имеют общих данных, они известны как взаимно независимые наборы. Давайте рассмотрим некоторые операции, основанные на отношениях между множествами:
Объединение множества
Объединение множества определяется как множество, содержащее все элементы, присутствующие в множестве A ИЛИ множестве B. Используется слово «ИЛИ». для представления объединения набора, что означает, что если данные существуют либо в A, либо в B, они будут частью Union набора. Символ, используемый для обозначения объединения множества, — «∪». Стандартное определение можно записать так: если x ∈ A ∪ B, то x ∈ A или x ∈ B. Диаграмма Венна для A ∪ B такова:
Свойства:
- A∪ B= B ∪ A [Переместительное свойство]
- (A ∪ B) ∪ C= A ∪ (B ∪ 2 A) ∪ 6 = 9013 9013 A
- A ∪ U= U
Хорошим практическим примером объединения двух наборов могут быть два друга, приглашающие других своих друзей на вечеринку, теперь существует высокая вероятность того, что между ними есть общие друзья, теперь нет смысла приглашать их дважды, следовательно, общие друзья приглашаются только один раз, а остальные друзья также приглашены, так будет выглядеть объединение набора друзей.

Пересечение набора
Пересечение набора определяется как множество, содержащее все элементы, присутствующие в наборе A и наборе B. Слово «И» используется для обозначения пересечения наборов, это означает, что элементы в пересечении присутствуют как в A, так и в B. Символ, используемый для обозначения пересечения множества, — «∩». Стандартное определение можно записать так: если x ∈ A ∩ B, то x ∈ A и x ∈ B. Диаграмма Венна для A ∩ B выглядит следующим образом:
Свойства
- A ∩ B= B ∩ A [Переместительное свойство]
- (A ∩ B) ∩ C= A ∩ (B ∩ C) [Ассоциативное свойство]
- A ∩ U= A A ∩ C
- ∅= ∅
Хорошим практическим примером пересечения двух множеств может быть такой: представьте, что двое друзей устраивают вечеринку и решили пригласить только тех друзей, которые являются их общими друзьями. Они записали имена своих друзей, а потом увидели общих друзей и пригласили только тех, это можно назвать Пересечением множества друзей.

Дополнение набора
Дополнение набора включает все данные, кроме данных набора. Данные, присутствующие в Универсальном наборе, за исключением данных самого набора, являются Дополнением набора. Дополнением дополнения множества является само множество. Обозначается как A’ или A c .
A’ или A c = U- A
Свойства:
- A ∪ A’= U
- A ∩ A’9= ∩ A’
Закон Де Моргана
Закон Де Моргана включает все три операции: объединение, пересечение и дополнение множества. Предположим, что n наборов задано как A1, A2, A3… Полное дополнение объединения всех этих множеств равно пересечению дополнений каждого из них.
(A1 ∪ A2 ∪ A3…. ∪ An)’ = A1′ ∩ A2′ ∩ A3’…. An’
Для двух наборов, A и B,
(A ∪ B)’= A’ ∩ B’
Примеры задач
Вопрос 1: Найдите объединение и пересечение множеств,
A = {1, 2, 3, 4, 5, 6}
B = {5, 6, 7, 8, 9 }
Решение:
Объединение множеств
A∪ B= {1, 2, 3, 4, 5, 6, 7, 8, 9}
Пересечение множеств A и B
A ∩ B = {5, 6}
Вопрос 2: Найдите пересечение и объединение множеств, приведенных ниже,
P = {a, e, i, o, u}
Q = {p, q, r, s, t}
R = {j, k, l, m, n}
Решение:
90 Объединение 2000 множеств P∪ Q∪ R= {a, e, i, o, u, p, q, r, s, t, j, k, l, m, n}
Пересечение множеств
P∩ Q∩ R = ∅
Пересечение множеств P, Q и R является нулевым множеством, поскольку среди трех множеств нет общих элементов.

Вопрос 3: Найдите дополнение, объединение и пересечение заданных множеств,
Универсальный набор, U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
X= {2, 4 , 6, 8, 10, 12, 14}
Y= {3, 6, 9, 12, 15}
Решение:
U= X’,
2 X= {1, 3, 5, 7, 9, 11, 13, 15}
Дополнение множества Y,
Y’= U- Y= {1, 2, 4, 5, 7, 8, 10, 11, 13, 14}
Объединение множеств,
X∪ Y= {2, 3, 4, 6, 8, 9, 10, 12, 14, 15}
Пересечение множеств,
X ∩ Y= {6, 12}
Вопрос 4: Докажите ассоциативность объединения множеств, множества A, B , и C приведены ниже,
A= {a, b, c, d, e}
B= {d, e, f, g, h}
C= {g, h, i, j, k}
Решение:
Ассоциативное свойство для объединения множеств,
(A ∪ B) ∪ C = A ∪ (B ∪ C) г, д, е, ж, з}
(A∪ B) ∪ C= {a, b, c, d, e, f, g, h, i, j, k}
Для RHS, B∪ C= {d, e, f, g , h, i, j, k}
A∪ (B∪ C)= {a, b, c, d, e, f, g, h, i, j, k}
Следовательно, LHS= RHS
Вопрос 5.
 Докажите закон Де Моргана для множеств A и B, приведенных ниже, когда универсальное множество задано как , 25, 26, 28, 30, 32, 34, 35, 36, 38, 40, 42, 44, 45, 46, 48, 50}
Докажите закон Де Моргана для множеств A и B, приведенных ниже, когда универсальное множество задано как , 25, 26, 28, 30, 32, 34, 35, 36, 38, 40, 42, 44, 45, 46, 48, 50} А= {10, 15, 20, 25, 30, 35, 40, 45, 50}
B= {10, 20, 30, 40, 50}
Решение:
LHS ⇢ A∪B= {10, 15, 20, 25, 30, 35, 40, 45, 50}
(A ∪ B)’= {12, 14, 16, 18, 22, 24, 26, 28 , 32, 34, 36, 38, 42, 44, 46, 48}
RHS ⇢ A’= {12, 14, 16, 18, 22, 24, 26, 28, 32, 34, 36, 38, 42 , 44, 46, 48}
B’= {12, 14, 15, 16, 18, 22, 24, 25, 26, 28, 32, 34, 35, 36, 38, 42, 44, 45, 46 , 48}
A’∩ B’= {12, 14, 16, 18, 22, 24, 26, 28, 32, 34, 36, 38, 42, 44, 46, 48}
Следовательно, LHS= RHS
Вопрос 6: Докажите ассоциативное свойство пересечения множеств для данных множеств,
A= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
B= {3, 6, 9, 12, 15, 18}
C= {2, 3, 6, 10, 12, 15, 18}
Решение:
Ассоциативное свойство для пересечения наборов A и B задается как,
(A ∩ B) ∩ C = A ∩ (B ∩ C)
LHS⇢ A ∩ B = {6, 12, 18}
(A ∩ B) ∩ C = {6, 12, 18}
RHS⇢ B∩ C= {3, 6, 12, 15, 18}
A∩ (B ∩ C)= {6, 12, 18}
Следовательно, LHS= RHS
Объединение множеств | Математические вкусности
Форма поиска
Поиск
В предыдущих уроках мы использовали диаграммы Венна для представления отношений между множествами.
 Давайте посмотрим на пример 1 ниже.
Давайте посмотрим на пример 1 ниже.Пример 1. В средней школе Гринвилля два класса будут объединены в один, чтобы сократить расходы. Если учащиеся оркестра и хора объединятся в один новый класс, то какие учащиеся будут в этом классе?
Дано: Дано = {Сэм, Киеша, Дерек, Лорри, Робин, Рауль, Ширли, Натан, Крис, Дана} , Группа = {Сэм, Лорри, Рауль, Дерек} и Хор = {Робин , Дерек, Киеша}, найдите Band Chorus.
Анализ: Эта задача требует от нас найти союз оркестра и хора. Чтобы решить эту проблему, мы должны перечислить всех учеников, которые находятся в группе, в хоре или в обеих группах.
Решение:
Объяснение:
Группа Хор = {Сэм, Лорри, Рауль, Дерек, Киеша, Робин}
Обратите внимание, что Дерек находится в их пересечении, поэтому Дерек находится в их обоих множествах, поэтому Дерек находится в их пересечении. Однако Дерек прописывается в союзе только один раз.
Определение: Объединение двух множеств A и B, — это множество элементов, которые находятся в A или в B или в обоих Обозначается A B , и читается как « A соединение B ».

Сравним объединение и пересечение.
Союз Перекресток записывается как А Б А Б читать как A соединение Б A пересечение B значение A или B или оба А и В как найти объединить все элементы найти элементы, общие для обоих Союз часто считают браком.
 Мы используем «и» для пересечения» и » или» для объединения. Давайте рассмотрим еще несколько примеров объединения двух множеств.
Мы используем «и» для пересечения» и » или» для объединения. Давайте рассмотрим еще несколько примеров объединения двух множеств.Пример 2: Let = {число чисел}, P = {кратное 3 меньше 20} и Q = {четные числа меньше 20}. Нарисуйте и подпишите диаграмму Венна, чтобы показать объединение P и Q .
Анализ: Заштрихуйте элементы, которые находятся в P или в Q в обоих . Заштрихованная область на диаграмме Венна ниже показывает P Q.
Решение:
Обозначения: P Q = {2, 3, 4, 8, 9, 10, 12, 15, 16, 16, 16, 16, 16, 16, 16 , 18}
Обратите внимание, что элементы 6, 12 и 18 находятся в обоих наборах (т. е. на пересечении P и Q ). Однако эти элементы пишутся в союзе только один раз.
Пример 3: Пусть = { k | 1 ≤ k ≤ 10 }, X = {1, 6, 9} и Y = {1, 3, 5, 6, 8, 9}.
 Нарисуйте и подпишите диаграмму Венна, чтобы показать X Y.
Нарисуйте и подпишите диаграмму Венна, чтобы показать X Y. Анализ: X является подмножеством Y . Таким образом, все элементы в X также содержатся в Y .
Объяснение: X Y = {1, 3, 5, 6, 8, 9}, which is equal to the set Y.
In example 3, since X Y , получаем X Y = 907 . Это отношение определено ниже.
Другой способ определения объединения двух множеств заключается в следующем:
A B = {x | x A или x B }
Пример 4: LET = {Animals}, A = { = {9149 {9141 = {9149 {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9141 = {9149.
 }. Нарисуйте и подпишите диаграмму Венна, чтобы показать A B .
}. Нарисуйте и подпишите диаграмму Венна, чтобы показать A B .Анализ: Эти множества не пересекаются и не имеют общих элементов. Таким образом, A B — все элементы в A и все элементы в B.
Объяснение: A B = {101490 A B = прямой союз двух наборов. Непересекающиеся множества не имеют общих элементов. Следовательно, союз A и B не имеет общих элементов. Поскольку невозможно, чтобы собаки в A также были кошками в B , мы уверены, что количество элементов в объединении равно сумме всех собак в A и все кошки в B . Таким образом, объединение получается в результате сложения всех элементов обоих наборов.
Союз из двух комплектов A и B, — это набор элементов, которые в A или в B или в оба.
 Он обозначается A B , и читается как « A union B ». Формальное определение союза показано ниже:
Он обозначается A B , и читается как « A union B ». Формальное определение союза показано ниже: А В = {x | x A или x B }
Упражнения. Выберите свой ответ, нажав на соответствующую кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку.
1. Указано = {яблоки, апельсины, бананы, груши} и = {Oranges, Pears, Frogse}, что представляет собой 94949494949494949494949494949494949494949494949494949494949949494994949949499499499499494994949949499494994949949499494949494949493 = {Oranges, Pears, Frogse}. 
P Q = Ø
P Q = {apples, oranges, bananas, pears}
P Q = {apples, oranges , бананы, груши, виноград}
Ничего из вышеперечисленного.ЯЩИК РЕЗУЛЬТАТОВ:
2. Дано = {простые числа} и = {составные числа}, что такое 0 90? A B = {целые числа}
A B = {числа > 1}
A B = {мнимые числа}
Все вышеперечисленное.
ЯЩИК РЕЗУЛЬТАТОВ:
3. Дано = {1, 4, 16} и = {1, 6 4, 1, 2, 9}0004 ? X Y = {1, 4, 9, 16, 25, 36}
X Y = {1, 4, 16}
X Y = Ø
Ничего из вышеперечисленного.ОКНО РЕЗУЛЬТАТОВ:
4. 
дано = {гласные} и = {Согласованные}, что является ?? P Q = Ø
P Q = {a, e, i, o, u}
P Q = { согласные}
P Q = {Английский алфавит}ЯЩИК РЕЗУЛЬТАТОВ:
5. 

 А. Н. Тихонова. – 3-е изд., перераб. и доп. – М.: Проспект, 2006. – Т. 1. – С. 66. – 672 с.
А. Н. Тихонова. – 3-е изд., перераб. и доп. – М.: Проспект, 2006. – Т. 1. – С. 66. – 672 с. 

 Предлагаю посмотреть небольшой видеоролик курса информатики «Понятие логики».
Предлагаю посмотреть небольшой видеоролик курса информатики «Понятие логики».
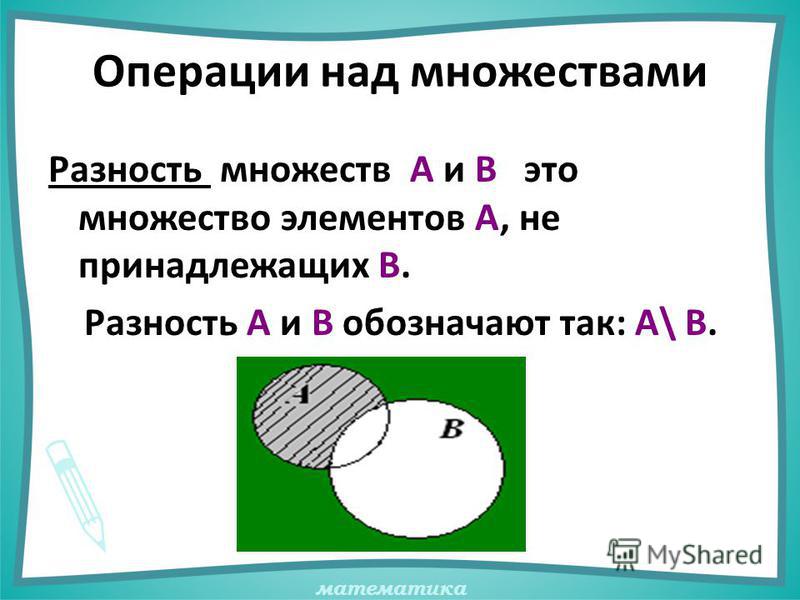
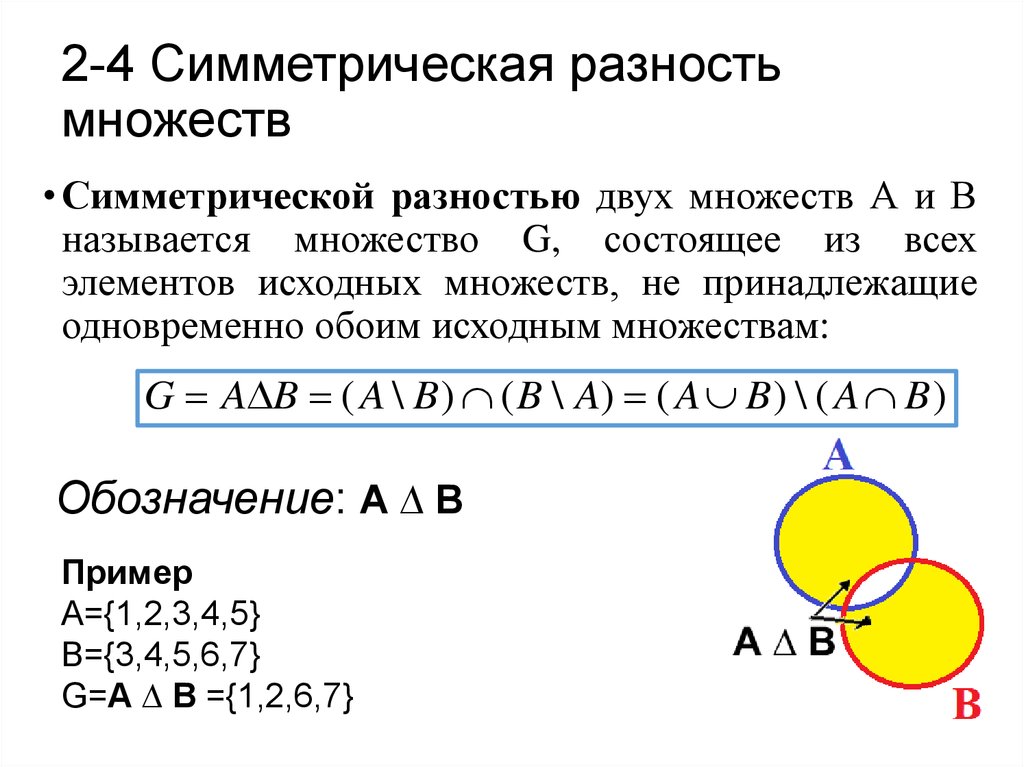 Могут изображать множества с помощью кругов Эйлера-Венна. Решают логические задачи.
Могут изображать множества с помощью кругов Эйлера-Венна. Решают логические задачи.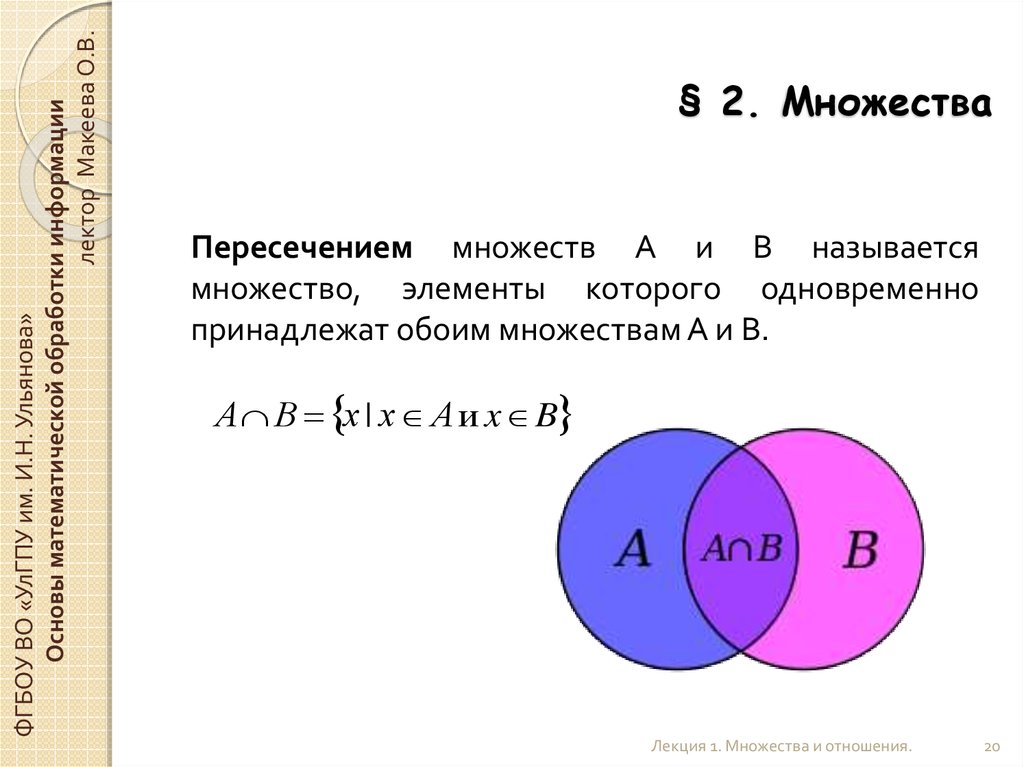 Всего в классе 38 человек. «Как приручить дракона» выбрал 21 ученик, среди которых трое назвали еще «Лови волну», шестеро – «Зверополис», а один написал все три мультфильма. Мультфильм «Лови волну» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Зверополис»?
Всего в классе 38 человек. «Как приручить дракона» выбрал 21 ученик, среди которых трое назвали еще «Лови волну», шестеро – «Зверополис», а один написал все три мультфильма. Мультфильм «Лови волну» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Зверополис»? 
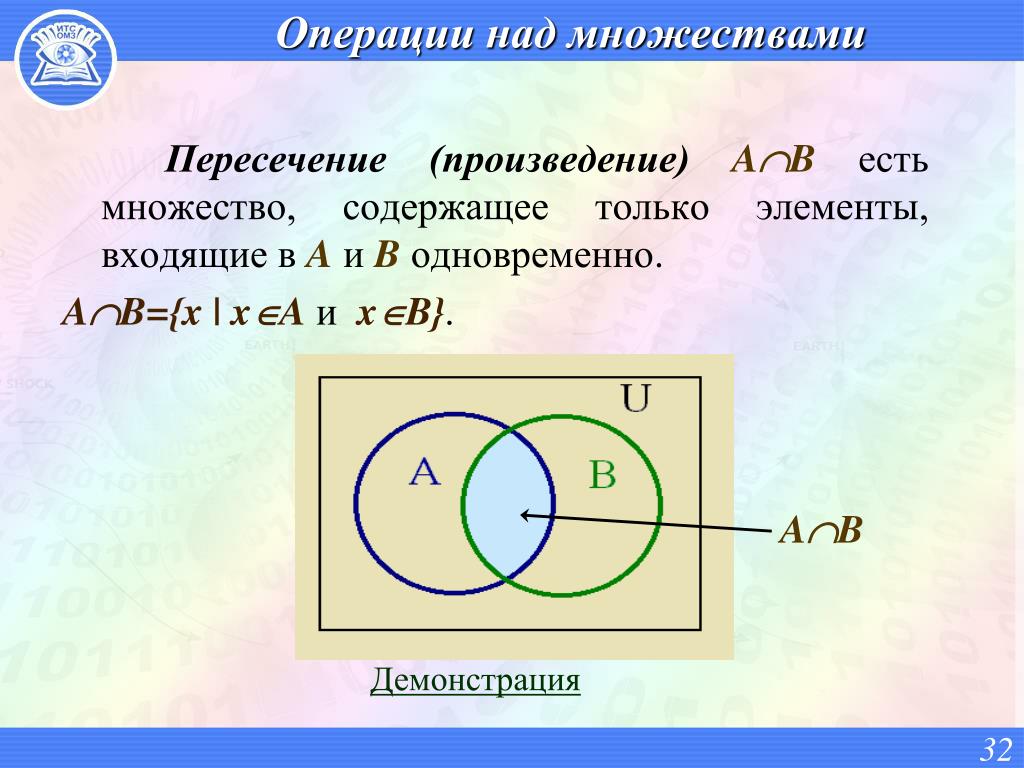 kz/ru/courses/informatika-ru/8-klass/lesson/ponyatie-logiki
kz/ru/courses/informatika-ru/8-klass/lesson/ponyatie-logiki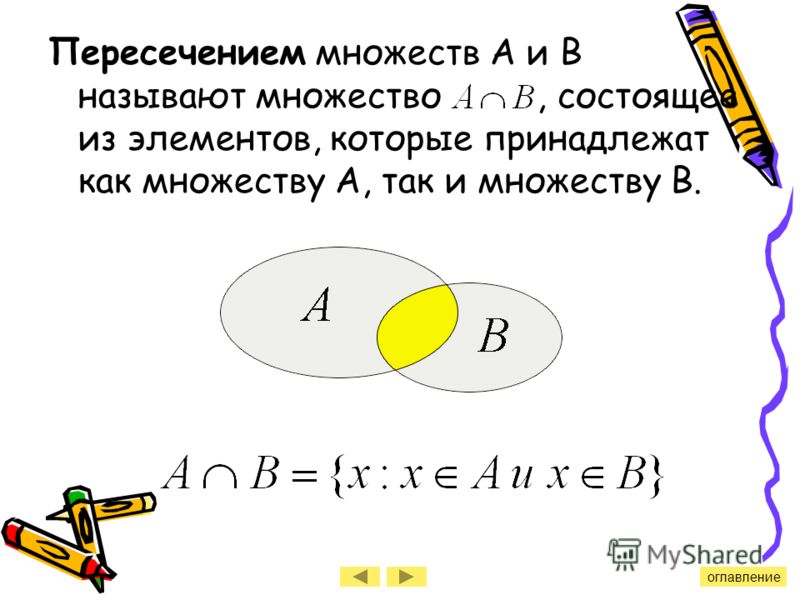 Пересечение множеств. Объединение множеств
Пересечение множеств. Объединение множеств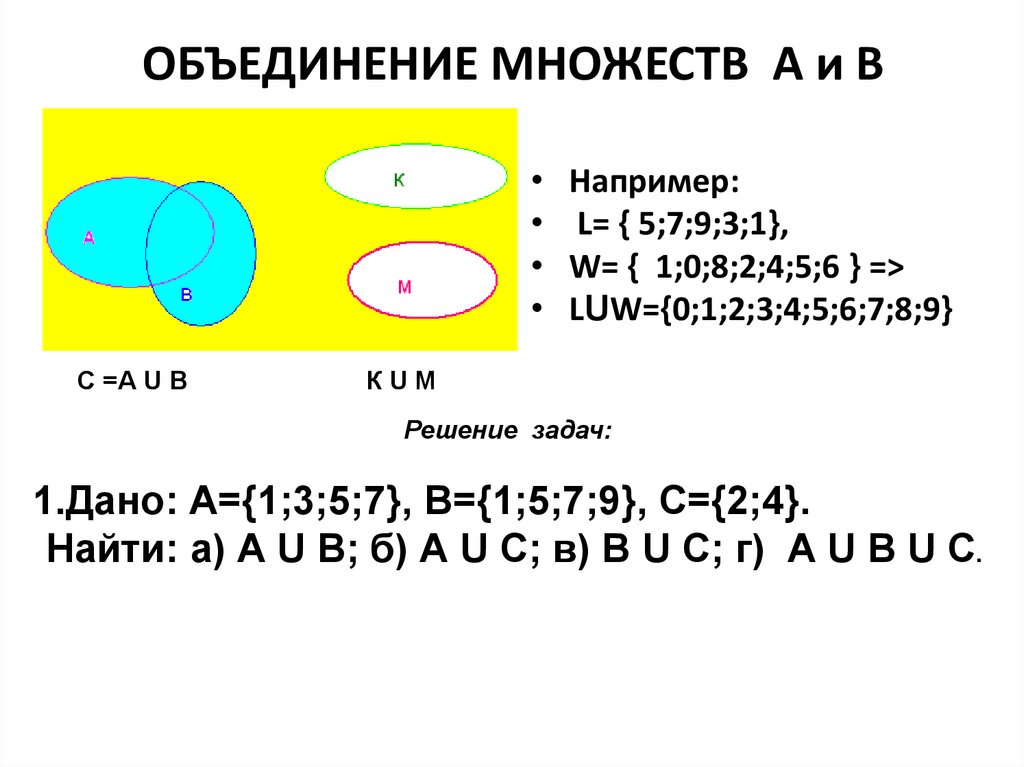 55kb.
55kb.
 78kb.
78kb.
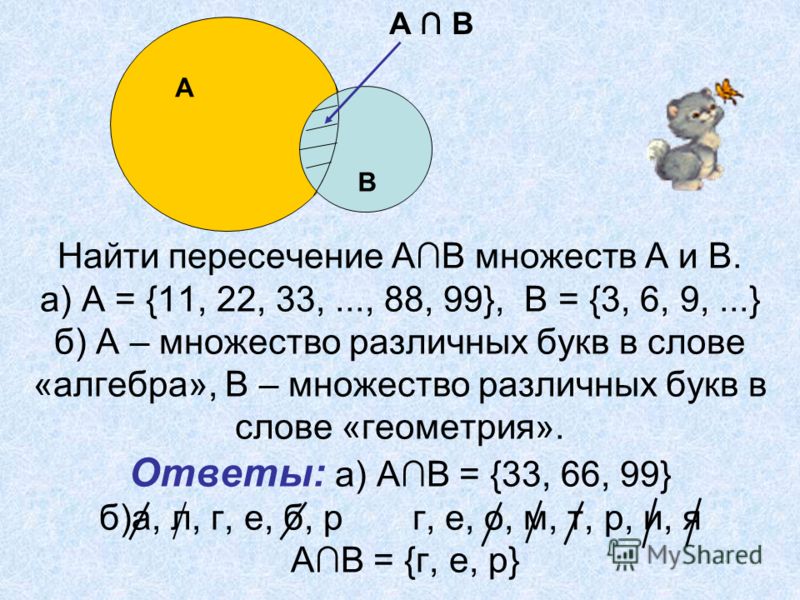 А. _________
А. _________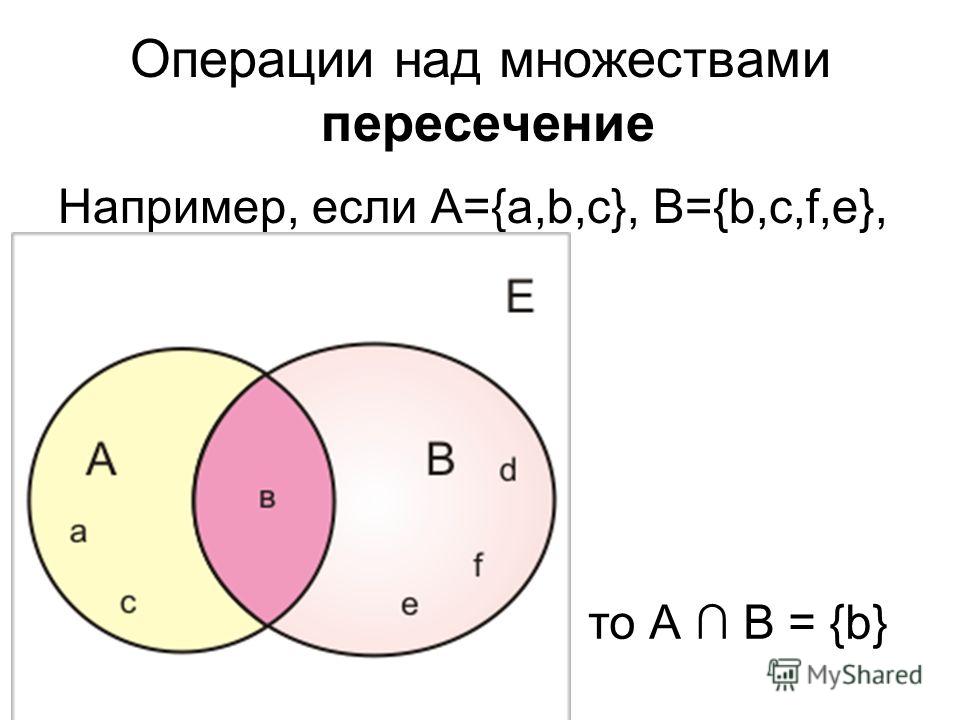 Какую тему мы проходили на прошлом уроке?
Какую тему мы проходили на прошлом уроке?
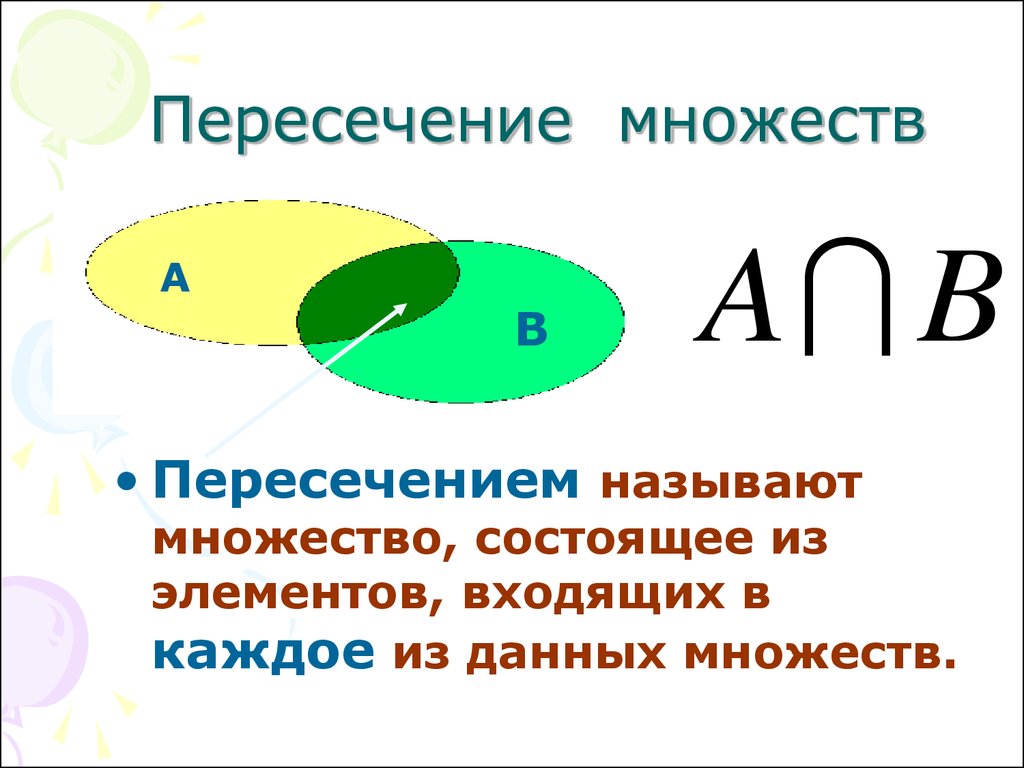 Всем понятно как мы это получили? В данном случае союз «и» можно не использовать.
Всем понятно как мы это получили? В данном случае союз «и» можно не использовать.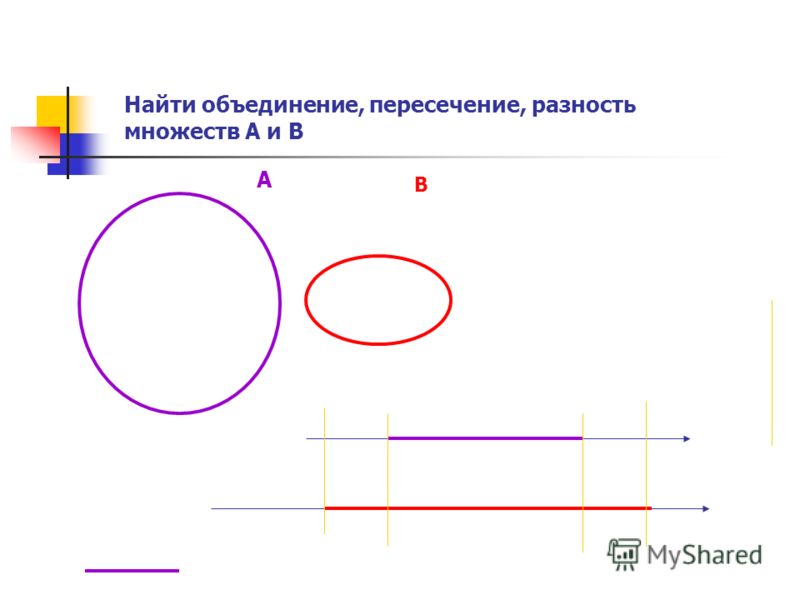 Запишите себе определение:
Запишите себе определение: Рассмотрим на примере. У нас есть два множества: А – чётных натуральных чисел, В – двузначных чисел. Составим новое свойство при помощи союза «или»: каждый элемент должен быть чётным натуральным числом или двузначным числом. Например в А U В может быть число 8, потому что оно чётное, хотя и однозначное, а может быть 37, хотя оно нечётное, но двузначное.
Рассмотрим на примере. У нас есть два множества: А – чётных натуральных чисел, В – двузначных чисел. Составим новое свойство при помощи союза «или»: каждый элемент должен быть чётным натуральным числом или двузначным числом. Например в А U В может быть число 8, потому что оно чётное, хотя и однозначное, а может быть 37, хотя оно нечётное, но двузначное.