Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Чему равен вписанный угол, который опирается на дугу, градусная мера которой равна 127°?
Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площад
Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площад
Задача: На прошлой неделе Саша прочитал3/7 всей книги, а на этой неделе- половину оставшихся страниц, да еще 20 и дочитал книгу до конца. Сколько
Решено
Найди первые четыре члена и 10-й член арифметической прогрессии (an), если общая формула an=9n−3. a1= a2= a3= a4= a10=
Решено
1). Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол, равный 60 градусам. Найдите отношение объёмов конуса и шара.
Пользуйтесь нашим приложением
Уравнение касательной к графику функции. Как найти угловой коэффициент уравнения
Прямая y = f(x) будет являться касательной к графику, изображенному на рисунке в точке х0 при том условии, если она проходит через данную точку с координатами (х0; f(x0)) и имеет угловой коэффициент f»(x0). Найти этот коэффициент, учитывая особенности касательной, несложно.
Найти этот коэффициент, учитывая особенности касательной, несложно.
Вам понадобится
- — математический справочник;
- — тетрадь;
- — простой карандаш;
- — ручка;
- — транспортир;
- — циркуль.
Инструкция
- Примите к сведению, что график дифференцируемой функции f(x) в точке х0 не имеет различий с отрезком касательной. Поэтому он является достаточно близким к отрезку l, к проходящему через точки (х0; f(х0)) и (х0+Δx; f(x0 + Δx)). Чтобы задать прямую, проходящую через точку А с коэффициентами (х0; f(х0)), укажите ее угловой коэффициент. При этом он равен Δy/Δx секущей касательной (Δх→0) , а также стремится к числу f‘(x0).
- Если значений f‘(x0) не существует, то, возможно, касательной нет, или же она проходит вертикально. Исходя из этого, присутствие производной функции в точке х0 объясняется существованием невертикальной касательной, которая соприкасается с графиком функции в точке (х0, f(х0)). В данном случае угловой коэффициент касательной равняется f»(х0).
 Становится понятен геометрический смысл производной, то есть расчет углового коэффициента касательной.
Становится понятен геометрический смысл производной, то есть расчет углового коэффициента касательной. - То есть для того чтобы найти угловой коэффициент касательной, нужно найти значение производной функции в точке касания. Пример: найти угловой коэффициент касательной к графику функции у = х³ в точке с абсциссой Х0 = 1. Решение: Найдите производную данной функции у΄(х) = 3х²; найдите значение производной в точке Х0 = 1. у΄(1) = 3 × 1² = 3. Угловой коэффициент касательной в точке Х0 = 1 равен 3.
- Начертите на рисунке дополнительные касательные таким образом, чтобы они соприкасались с графиком функции в следующих точках: x1, х2 и х3. Отметьте углы, которые образуются данными касательными с осью абсцисс (угол отсчитывается в положительном направлении — от оси до касательной прямой). Например, первый угол α1 будет острым, второй же (α2) – тупой, ну а третий (α3) будет равняться нулю, так как проведенная касательная прямая является параллельной оси ОХ. В этом случае тангенс тупого угла есть отрицательное значение, а тангенс острого угла – положительное, при tg0 и результат равен нулю.

В математике одним из параметров, описывающих положение прямой на декартовой плоскости координат, является угловой коэффициент этой прямой. Этот параметр характеризует наклон прямой к оси абцисс. Чтобы понять, как найти угловой коэффициент, сначала вспомним общий вид уравнения прямой в системе координат XY.
В общем виде любую прямую можно представить выражением ax+by=c, где a, b и c — произвольные действительные числа, но обязательно a 2 + b 2 ≠ 0.
Подобное уравнение с помощью несложных преобразований можно довести до вида y=kx+d, в котором k и d — действительные числа. Число k является угловым коэффициентом, а само уравнение прямой подобного вида называется уравнением с угловым коэффициентом. Получается, что для нахождения углового коэффициента, необходимо просто привести исходное уравнение к указанному выше виду. Для более полного понимания рассмотрим конкретный пример:
Задача: Найти угловой коэффициент линии, заданной уравнением 36x — 18y = 108
Решение: Преобразуем исходное уравнение.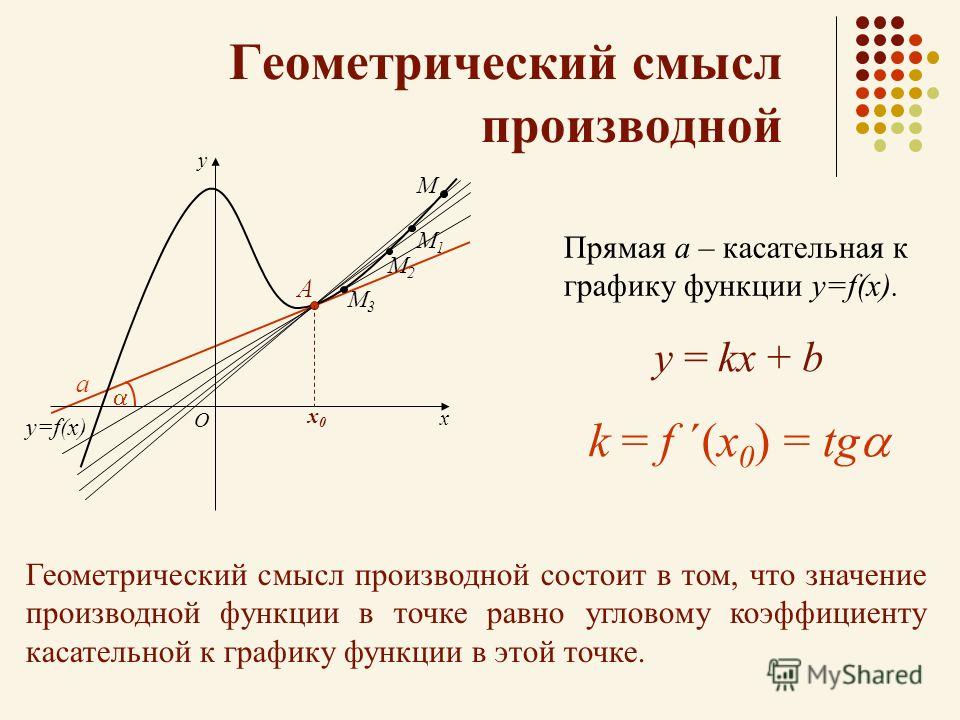
Ответ: Искомый угловой коэффициент данной прямой равен 2.
В случае, если в ходе преобразований уравнения мы получили выражение типа x = const и не можем в результате представить y в виде функции x, то мы имеем дело с прямой, параллельной оси Х. Угловой коэффициент подобной прямой равен бесконечности.
Для прямых, которых выражены уравнением типа y = const, угловой коэффициент равняется нулю. Это характерно для прямых, параллельных оси абцисс. Например:
Задача: Найти угловой коэффициент линии, заданной уравнением 24x + 12y — 4(3y + 7) = 4
Решение: Приведем исходное уравнение к общему виду
24x + 12y — 12y + 28 = 4
Из полученного выражения выразить y невозможно, следовательно угловой коэффициент данной прямой равен бесконечности, а сама прямая будет параллельна оси Y.
Геометрический смысл
Для лучшего понимания обратимся к картинке:
На рисунке мы видим график функции типа y = kx. Для упрощения примем коэффициент с = 0. В треугольнике ОАВ отношение стороны ВА к АО будет равно угловому коэффициенту k.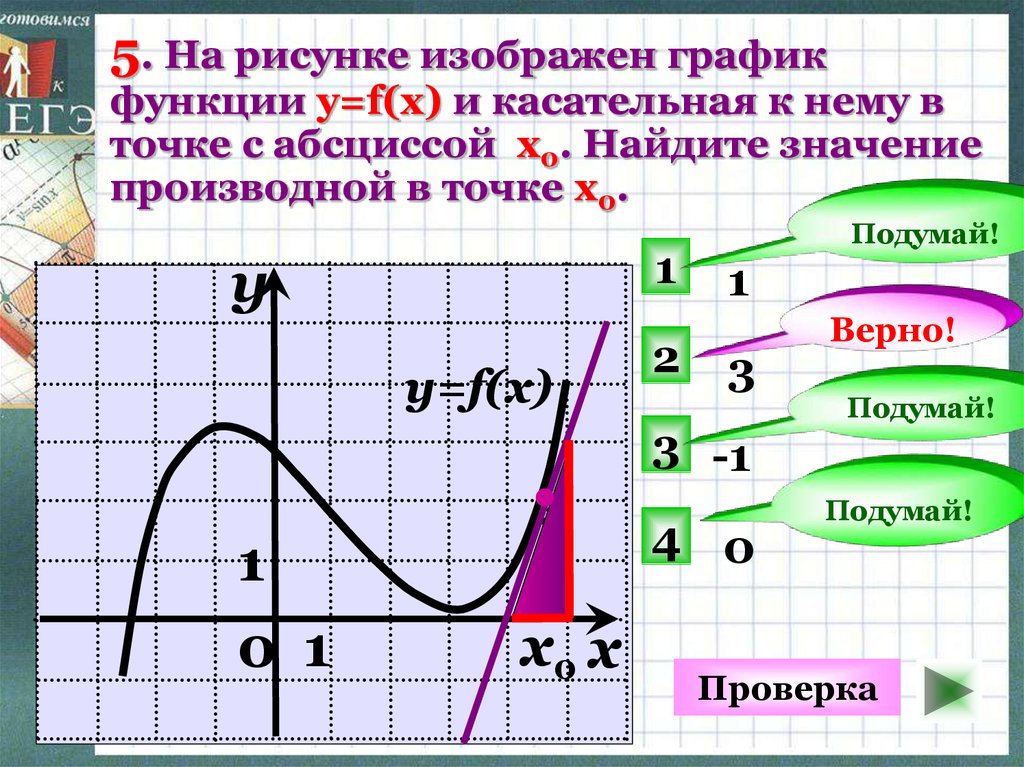 Вместе с тем отношение ВА/АО — это тангенс острого угла α в прямоугольном треугольнике ОАВ. Получается, что угловой коэффициент прямой равняется тангенсу угла, который составляет эта прямая с осью абцисс координатной сетки.
Вместе с тем отношение ВА/АО — это тангенс острого угла α в прямоугольном треугольнике ОАВ. Получается, что угловой коэффициент прямой равняется тангенсу угла, который составляет эта прямая с осью абцисс координатной сетки.
Решая задачу, как найти угловой коэффициент прямой, мы находим тангенс угла между ней и осью Х сетки координат. Граничные случаи, когда рассматриваемая прямая параллельна осям координат, подтверждают вышенаписанное. Действительно для прямой, описанной уравнением y=const, угол между ней и осью абцисс равен нулю. Тангенс нулевого угла также равен нулю и угловой коэффициент тоже равен нулю.
Для прямых, перпендикулярных оси абцисс и описываемых уравнением х=const, угол между ними и осью Х равен 90 градусов. Тангенс прямого угла равен бесконечности, так же и угловой коэффициент подобных прямых равен бесконечности, что подтверждает написанное выше.
Угловой коэффициент касательной
Распространенной, часто встречающейся на практике, задачей является также нахождение углового коэффициента касательной к графику функции в некоторой точке. Касательная — это прямая, следовательно к ней также применимо понятие углового коэффициента.
Касательная — это прямая, следовательно к ней также применимо понятие углового коэффициента.
Чтобы разобраться, как найти угловой коэффициент касательной, нам будет необходимо вспомнить понятие производной. Производная от любой функции в некоторой точке — это константа, численно равная тангенсу угла, который образуется между касательной в указанной точке к графику этой функции и осью абцисс. Получается, что для определения углового коэффициента касательной в точке x 0 , нам необходимо рассчитать значение производной исходной функции в этой точке k = f»(x 0). Рассмотрим на примере:
Задача: Найти угловой коэффициент линии, касательной к функции y = 12x 2 + 2xe x при х = 0,1.
Решение: Найдем производную от исходной функции в общем виде
y»(0,1) = 24 . 0,1 + 2 . 0,1 . e 0,1 + 2 . e 0,1
Ответ: Искомый угловой коэффициент в точке х = 0,1 равен 4,831
Инструкция
Определяем угловой коэффициент касательной к кривой в точке М.
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).
Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.
Найдите значение абсциссы точки касания, которую обозначаются буквой «а». Если она совпадает с заданной точкой касательной, то «а» будет ее х-координате. Определите значение
Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».
Возьмите общее уравнение касательной, которое определяется как y = f(a) = f (a)(x – a), и подставьте в него найденные значения a, f(a), f «(a). В результате будет найдено решение графика и касательной.
Решите задачу иным способом, если заданная точка касательной не совпала с точкой касания. В этом случае необходимо в уравнение касательной вместо цифр подставить «а». После этого вместо букв «х» и «у» подставьте значение координат заданной точки. Решите получившееся уравнение, в котором «а» является неизвестной. Поставьте полученное значение в уравнение касательной.
Составьте уравнение касательной с буквой «а», если в условии задачи задано уравнение функции и уравнение параллельной линии относительно искомой касательной. После этого необходимо производную функции , чтобы координату у точки «а». Подставьте соответствующее значение в уравнение касательной и решите функцию.
Пусть дана функция f , которая в некоторой точке x 0 имеет конечную производную f (x 0). Тогда прямая, проходящая через точку (x 0 ; f (x 0)), имеющая угловой коэффициент f ’(x 0), называется касательной.
А что будет, если производная в точке x 0 не существует? Возможны два варианта:
- Касательная к графику тоже не существует.
 Классический пример — функция y
= |x
| в точке (0; 0).
Классический пример — функция y
= |x
| в точке (0; 0). - Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π /2).
Уравнение касательной
Всякая невертикальная прямая задается уравнением вида y = kx + b , где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x 0 , достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f (x ), которая имеет производную y = f ’(x ) на отрезке . Тогда в любой точке x 0 ∈ (a ; b ) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x 0) · (x − x 0) + f (x 0)
Здесь f ’(x 0) — значение производной в точке x 0 , а f (x 0) — значение самой функции.
Задача. Дана функция y = x 3 . Составить уравнение касательной к графику этой функции в точке x 0 = 2.
Уравнение касательной: y
= f
’(x
0) · (x
− x
0) + f
(x
0). Точка x
0 = 2 нам дана, а вот значения f
(x
0) и f
’(x
0) придется вычислять.
Точка x
0 = 2 нам дана, а вот значения f
(x
0) и f
’(x
0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f
(x
0) = f
(2) = 2 3 = 8;
Теперь найдем производную: f
’(x
) = (x
3)’ = 3x
2 ;
Подставляем в производную x
0 = 2: f
’(x
0) = f
’(2) = 3 · 2 2 = 12;
Итого получаем: y
= 12 · (x
− 2) + 8 = 12x
− 24 + 8 = 12x
− 16.
Это и есть уравнение касательной.
Задача. Составить уравнение касательной к графику функции f (x ) = 2sin x + 5 в точке x 0 = π /2.
В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:
f
(x
0) = f
(π
/2) = 2sin (π
/2) + 5 = 2 + 5 = 7;
f
’(x
) = (2sin x
+ 5)’ = 2cos x
;
f
’(x
0) = f
’(π
/2) = 2cos (π
/2) = 0;
Уравнение касательной:
y = 0 · (x − π /2) + 7 ⇒ y = 7
В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k
= 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.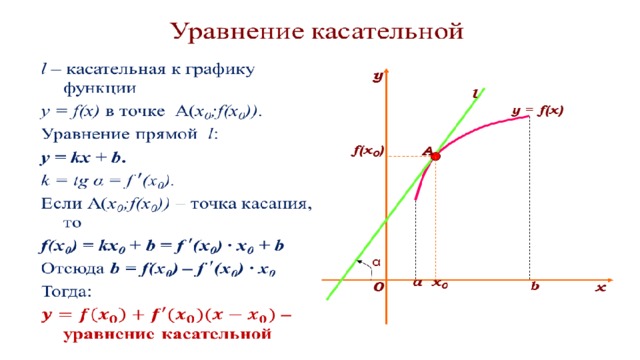
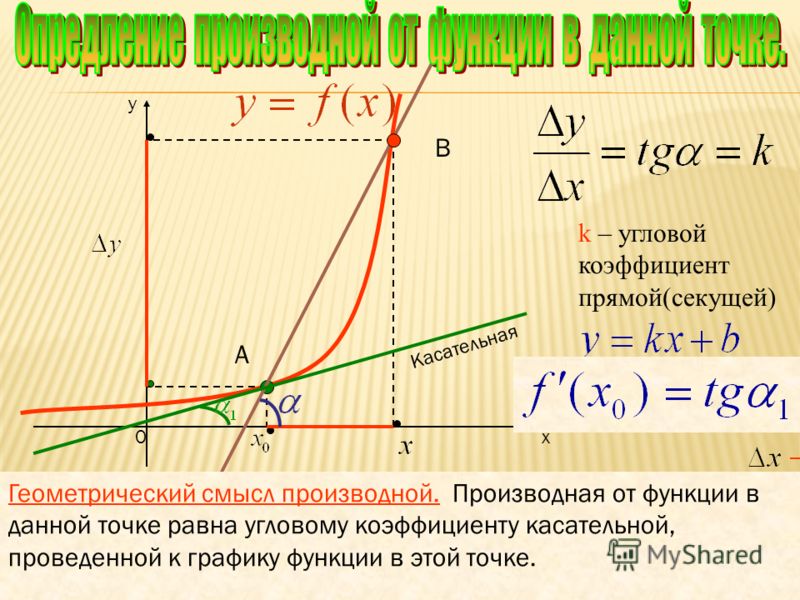
С понятием касательной к графику функции вы уже знакомы. График дифференцируемой в точке х 0 функции f вблизи х 0 практически не отличается от отрезка касательной, а значит, он близок к отрезку секущей l, проходящей через точки (х 0 ; f (х 0)) и (х 0 +Δx; f (x 0 + Δx)). Любая из таких секущих проходит через точку А (х 0 ; f (х 0)) графика (рис. 1). Для того чтобы однозначно задать прямую, проходящую через данную точку A, достаточно указать ее угловой коэффициент. Угловой коэффициент Δy/Δx секущей при Δх→0 стремится к числу f ‘(x 0) (его мы примем за угловой коэффициент касательной) Говорят, что касательная есть предельное положение секущей при Δх→0 .
Если же f’(х 0) не существует, то касательная либо не существует (как у функции у = |x| в точке (0; 0), см. рис.), либо вертикальна (как у графика функции в точке (0; 0), рис.2).
Итак, существование производной функции f в точке хо эквивалентно существованию (невертикальной) касательной в точке (х 0 , f (х 0)) графика, при этом угловой коэффициент касательной равен f» (х 0). В этом состоитгеометрический смысл производной
В этом состоитгеометрический смысл производной
Касательная к графику дифференцируемой в точке xо функции f — это прямая, проходящая через точку (x 0 ; f (x 0)) и имеющая угловой коэффициент f ‘(х 0).
Проведем касательные к графику функции f в точках x 1 , х 2 , х 3 (рис. 3) и отметим углы, которые они образуют с осью абсцисс. (Это угол, отсчитываемый в положительном направлении от положительного направления оси до прямой.) Мы видим, что угол α 1 острый, угол α 3 тупой, а угол α 2 равен нулю, так как прямая l параллельна оси Ох. Тангенс острого угла положителен, тупого — отрицателен, tg 0 = 0. Поэтому
F»(x 1)>0, f’(x 2)=0, f’(x 3)
Построение касательных в отдельных точках позволяет более точно строить эскизы графиков. Так, например, для построения эскиза графика функции синус предварительно находим, что в точках 0; π/2 и π производная синуса равна 1; 0 и -1 соответственно.
Построим прямые, проходящие через точки (0; 0), (π/2,1) и (π, 0) с угловыми коэффициентами 1, 0 и -1 соответственно (рис.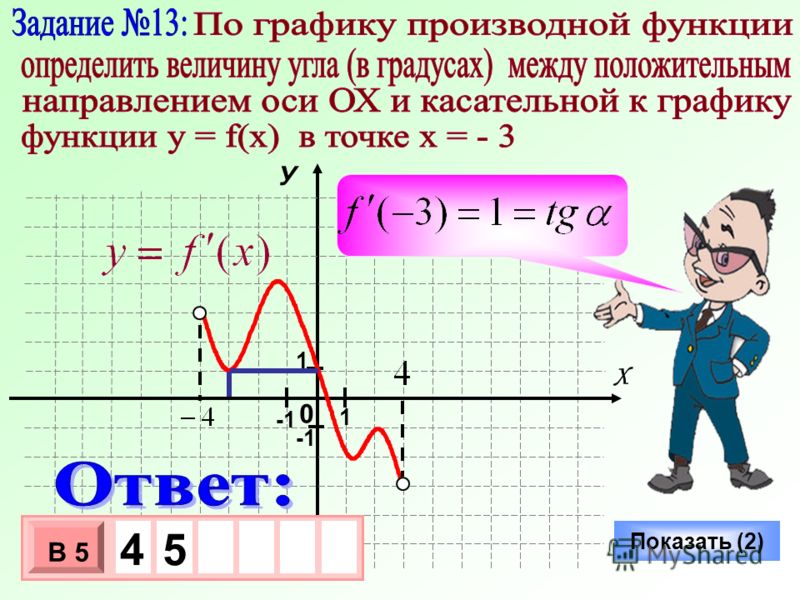 4) Остается вписать в полученную трапецию, образованную этими прямыми и прямой Ох, график синуса так, чтобы при х, равном 0, π/2 и π, он касался соответствующих прямых.
4) Остается вписать в полученную трапецию, образованную этими прямыми и прямой Ох, график синуса так, чтобы при х, равном 0, π/2 и π, он касался соответствующих прямых.
Отметим, что график синуса в окрестности нуля практически не отличим от прямой у = х. Пусть, например, масштабы по осям выбраны так, что единице соответствует отрезок в 1см. Имеем sin 0,5 ≈ 0,479425, т. е. |sin 0,5 — 0,5| ≈ 0,02, и в выбранном масштабе это соответствует отрезку длиной 0,2 мм. Поэтому график функции y = sin x в интервале (-0,5; 0,5) будет отклоняться (в вертикальном направлении) от прямой у = х не более чем на 0,2 мм, что примерно соответствует толщине проводимой линии.
Как найти наклон касательной?
Чтобы найти наклон касательной, мы должны иметь четкое представление о касательных и наклоне. Наклон определяется как отношение разницы координаты y к разнице координаты x. Он представлен следующей формулой:
m =( y 2 – y 1 ) 2 – x 1 )
Следует отметить, что:
- tan θ такой же, как m.
 Наклоны могут быть положительными или отрицательными в зависимости от того, движется ли линия вверх или вниз.
Наклоны могут быть положительными или отрицательными в зависимости от того, движется ли линия вверх или вниз. - Произведения наклона двух перпендикулярных прямых равны -1, а наклоны параллельных прямых одинаковы.
- Производная функции дает изменение скорости относительно изменения независимой переменной.
Наклон касательной линии
Касательная линия — это линия, которая касается кривой в точке. Могут быть касательные линии, которые позже пересекают кривую или касаются кривой в некоторых других точках. Но основные критерии того, чтобы прямая была касательной к кривой f(x) в точке x=a, если прямая проходит через точку (a, f(a)) (где точка является общей как для кривой, так и для касательная), а касательная имеет наклон f'(a), где f'(a) — производная функции f(x) в точке a.
Как найти наклон касательной?Наклон касательной равен производной кривой в некоторой точке. Формула для касательной с наклоном m и заданной точкой (x 1 , y 1 ) определяется как,
y – y 1 = M × (x — X 1 )
или
Y = MX + C
, где C — константа
Решение:
Аналогичные задачиНаклон касательной можно найти, найдя производную кривой f(x) и найдя значение производной в точке, где пересекаются касательная и кривая.
Это дает нам наклон
Например: Найдите наклон касательной к кривой f(x) = x² в точке (1, 2). Также найдите уравнение касательной.
Найдем производную от f (x):
f'(x) = dy/dx = d(x²) /dx = 2x
Значение наклона в точке (1, 2) равно
f'(x) = 2(1) = 2
Уравнение касательной равно
y – 2 = 2(x – 1)
или
y = 2x
Задача 1: Найдите наклон касательной линии 6y = 3x + 5.
Решение:
С имеет форму y= mx + c, где m — наклон
Мы можем написать,
y= (3x + 5 ) / 6
Следовательно, значение наклона равно 0,5 .
Задача 2. Найдите наклон по двум точкам (6, 7) и (8, 0).
Решение:
Наклон любых двух точек, скажем, (a, b) и (x, y) определяется выражением
m = (y-b) /(x-a) 7) /(8-6) = -3,5
Задача 3: найти наклон кривой y= 6x³.
Решение :
Наклон кривой определяется дифференцированием кривой: y= 3x+8
Решение:
Пусть наклон двух перпендикулярных линий равен m и n
m×n = -1
m=3
0 -1/3
Задача 5. Найдите наклон касательной к кривой f(x) = x⁴ в точке (2, 1). Также найдите уравнение касательной.
Решение:
Найдем производную кривой как 32
Уравнение касательной в точке (2, 1) есть,
y – 1 = 32(x – 2)
2. Наклон касательной к кривой (численный подход)
М. Борна
Поскольку мы можем моделировать многие физические проблемы с помощью кривых, важно получить представление о наклоны кривых в различных точках и что означает наклон в реальных приложениях.
ПРИМЕЧАНИЕ
В этом разделе мы покажем вам один из исторических подходов к нахождению наклонов касательных до того, как была разработана дифференциация.
Это для того, чтобы дать вам представление о том, как это работает.
Если вы хотите узнать, как находить наклоны (градиенты) касательных непосредственно с помощью производных, перейдите к разделу Касательные и нормали в главе «Приложения дифференцирования».
Помните: Пытаемся найти скорость изменения одной переменной по сравнению с другой.
Приложения включают:
- Изменение температуры в определенное время
- Скорость падающего объекта в определенное время
- Ток в цепи в определенное время
- Изменение цен на фондовом рынке в определенное время
- Прирост населения в определенное время
- Повышение температуры по мере увеличения плотности газа
Позже мы увидим, как найти эти скорости изменения, дифференцируя функцию и подставляя значение. Сейчас мы собираемся найти скорость изменения численно (то есть, подставляя числа, пока не найдем приемлемое приближение).
Мы рассматриваем общий случай и пишем наши функции с участием знакомые x (независимые) и y (зависимые) переменные.
Py = f(x)msОткрыть изображение на новой страницеНаклон касательной на P .
Наклон кривой y = f ( x ) в точке P означает наклон касательной в точке P . Нам нужно найти этот наклон для решения многих задач, поскольку он сообщает нам скорость изменения в конкретный момент времени. мгновенный.
[Мы пишем y = f ( х ) на кривой, начиная с и , является функцией x . То есть, поскольку x изменяется, y также изменяется.]
Дельта-обозначение
В этой работе мы пишем
- изменить в у как Δ у
- изменение x как Δ x
По определению уклон определяется как:
`m=(текст(изменение в)\ y)/(текст(изменение в)\ x)=(Deltax)/(Deltax)=(y_2-y_1)/(x_2-x_1)`
Мы используем это, чтобы найти численное решение наклона кривой.
Пример
Найдите наклон кривой y = x 2 в точке `(2,4)`, используя числовой метод .
Решение
Начнем с точки `Q(1, 1)`, которая находится где-то рядом с `P(2,4)`:
12-1-212345xyP (2, 4)Q (1, 1)y = f(x)msОткрыть изображение на новой страницеНаклон PQ .
Наклон PQ определяется как:
`m=(y_2-y_1)/(x_2-x_1)`
`=(4-1)/(2-1)`
`=3`
Теперь мы перемещаем Q дальше по кривой, чтобы она оказалась ближе к P . Давайте использовать `Q(1.5,2.25)`, который ближе к `П(2,4)`:
12-1-212345xyy = f(x)msP (2, 4)
Q (1.5, 2.25)
Наклон PQ — ближе к P
0Склон PQ теперь выдается:
`m=(y_2-y_1)/(x_2-x_1)`
`=(4-2,25)/(2-1,5)`
`=3,5`
Мы видим, что это уже довольно хорошее приближение к касательной в точке P , но недостаточно хорошее.
Теперь мы переместим Q еще ближе к P, скажем `Q(1.9,3.61)`.
Теперь у нас есть:
12-1-212345xyP (2, 4)Q (1.9, 3.61)y = f(x)msОткрыть изображение на новой страницеНаклон PQ — очень близко к Р
Итак,
`m=(y_2-y_1)/(x_2-x_1)`
`=(4-3,61)/(2-1,9)`
`=3,9`
Мы видим, что мы очень близки к требуемому наклону.
Теперь, если Q переместить в `(1.99,3.9601)`, тогда наклон PQ будет `3,99`.
Если Q равно `(1,999,3,996001)`, то наклон равен `3,999`.
Очевидно, что при `x → 2` наклон `PQ → 4`. Но заметьте, что на самом деле мы не можем принять `x = 2`, так как дробь для m будет иметь «0» внизу, и поэтому он будет неопределенным.
Мы обнаружили, что скорость изменения y по отношению к x составляет «4» единицы в точке «x = 2».
Исследуйте
Изучите этот пример с помощью интерактивного апплета на следующей странице:
3.

 04.20
04.20 Становится понятен геометрический смысл производной, то есть расчет углового коэффициента касательной.
Становится понятен геометрический смысл производной, то есть расчет углового коэффициента касательной.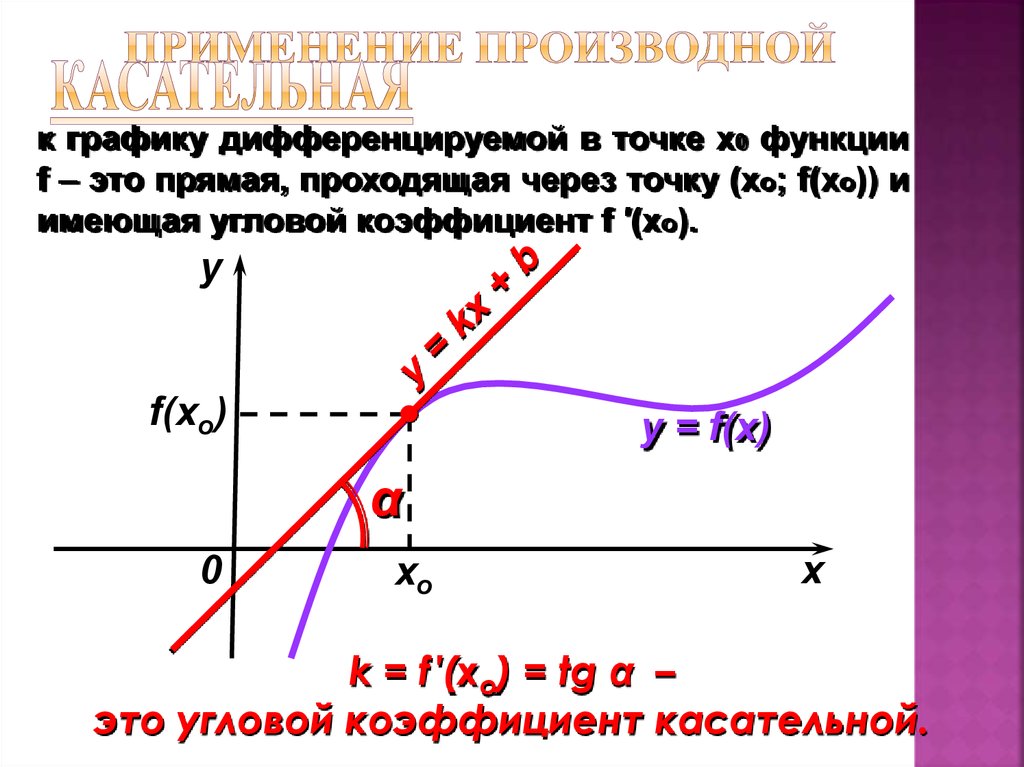
 Классический пример — функция y
= |x
| в точке (0; 0).
Классический пример — функция y
= |x
| в точке (0; 0).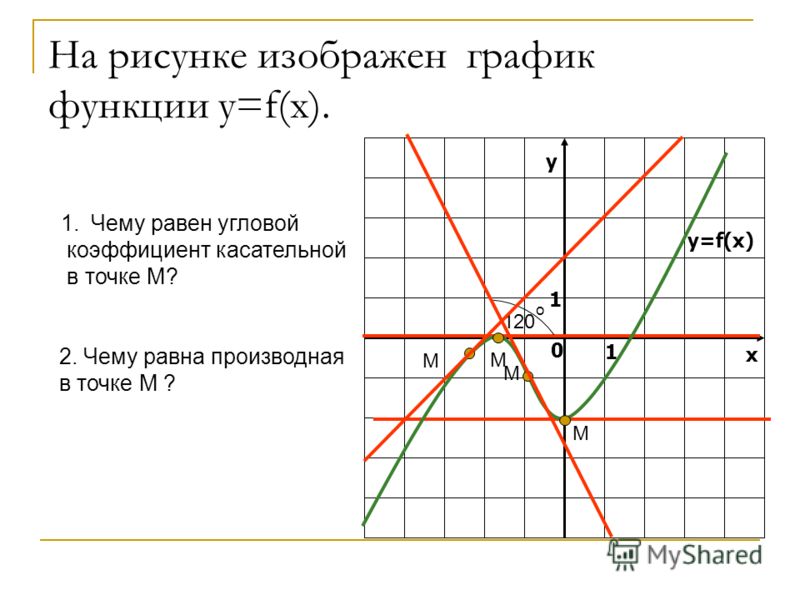 Наклоны могут быть положительными или отрицательными в зависимости от того, движется ли линия вверх или вниз.
Наклоны могут быть положительными или отрицательными в зависимости от того, движется ли линия вверх или вниз.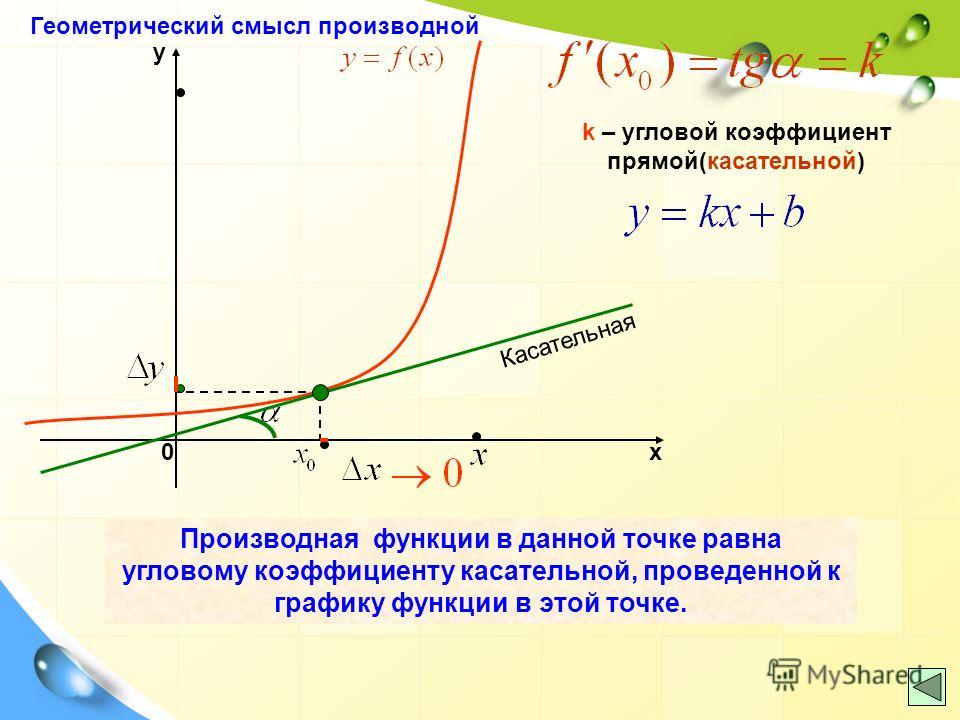 Это дает нам наклон
Это дает нам наклон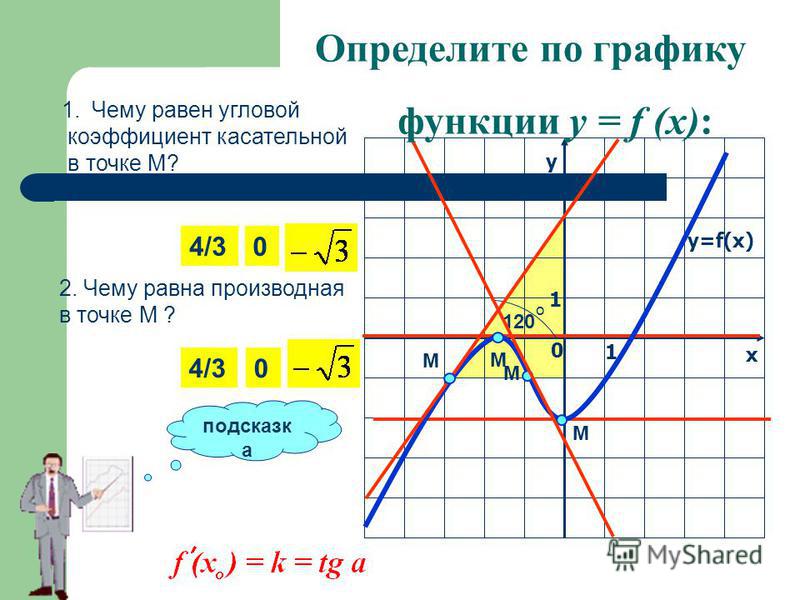 Это для того, чтобы дать вам представление о том, как это работает.
Это для того, чтобы дать вам представление о том, как это работает.