Все про окружность геометрия: Окружность: радиус, хорда, диаметр и дуга

alexxlab / / Разное

Содержание

Вписанная окружность

Главная » геометрия

Обновлено

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

  • Треугольник
  • Выпуклый, правильный многоугольник
  • Квадрат
  • Равнобедренная трапеция
  • Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм

, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Содержание

  1. Свойства вписанной окружности
  2. В треугольник
  3. В четырехугольник
  4. Примеры вписанной окружности
  5. Верные и неверные утверждения
  6. Окружность вписанная в угол

Свойства вписанной окружности

В треугольник
  1.  В любой треугольник может быть вписана окружность, причем только один раз.
  2.  Центр вписанной окружности — точка пересечения биссектрис треугольника.
  3.  Вписанная окружность касается всех сторон треугольника.
  4.  Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

    \[ S = \frac{1}{2}(a+b+c) \cdot r = pr \]

    p —  полупериметр четырехугольника. 2 — 2Rr} \]

    с — расстояние между центрами вписанной и описанной окружностей треугольника.
    R — радиус описанной около треугольника.
    r — радиус вписанной окружности треугольника.

В четырехугольник
  1. Не во всякий четырехугольник можно вписать окружность.
  2. Если у четырехугольника суммы длин его противолежащих
    сторон равны, то окружность, может быть, вписана (Теорема Пито).
  3. Центр вписанной окружности и середины двух
    диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона
    ).
  4. Точка пересечения биссектрис — это центр вписанной окружности.
  5. Точка касания — это точка, в которой соприкасается
    окружность и любая из сторон четырехугольника.
  6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

    \[ S = \frac{1}{2}(a+b+c+d)\cdot r = pr \]

    p —  полупериметр четырехугольника.
    r — радиус вписанной окружности четырехугольника.

  7. Точка касания вписанной окружности, которая лежит на любой из сторон,
    равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

  • Треугольник
  • Четырехугольник
  • Многоугольник

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, 

квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

  1. Радиус вписанной окружности в треугольник и радиус вписанной
    в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
  2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
  3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
  4. В любой ромб можно вписать окружность. Верное утверждение.
  5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
  6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
  7. Угол вписанный в окружность равен соответствующему центральному
    углу опирающемуся на ту же дугу. Неверное утверждение.
  8. Радиус вписанной окружности в прямоугольный треугольник равен
    половине разности суммы катетов и гипотенузы. Верное утверждение.
  9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
  10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,

в общей сложности два перпендикуляра со смежных сторон.

Центральный угол вписанной окружности – это угол, вершина
которого лежит в центре вписанной окружности.

Вписанный угол вписанной окружности – это угол,
вершина которого лежит на вписанной окружности.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Так-же читайте статью про треугольник вписанный в окружность.

8 класс. Геометрия. Окружность. Вписанный угол. Центральный угол. — Теорема о вписанном угле.

Комментарии преподавателя

Тео­ре­ма о впи­сан­ном угле

На­пом­ним неко­то­рые опре­де­ле­ния

Опре­де­ле­ние:

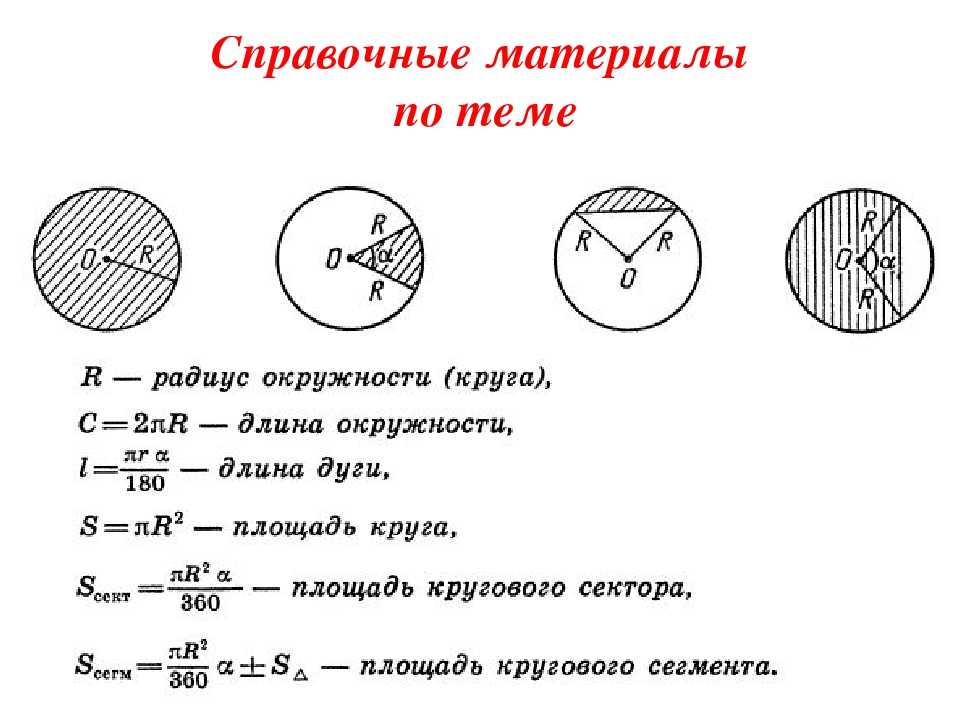
Окруж­но­стью с цен­тром в точке О и ра­ди­у­сом R на­зы­ва­ют мно­же­ство всех точек плос­ко­сти, уда­лен­ных от точки О на рас­сто­я­ние R (см.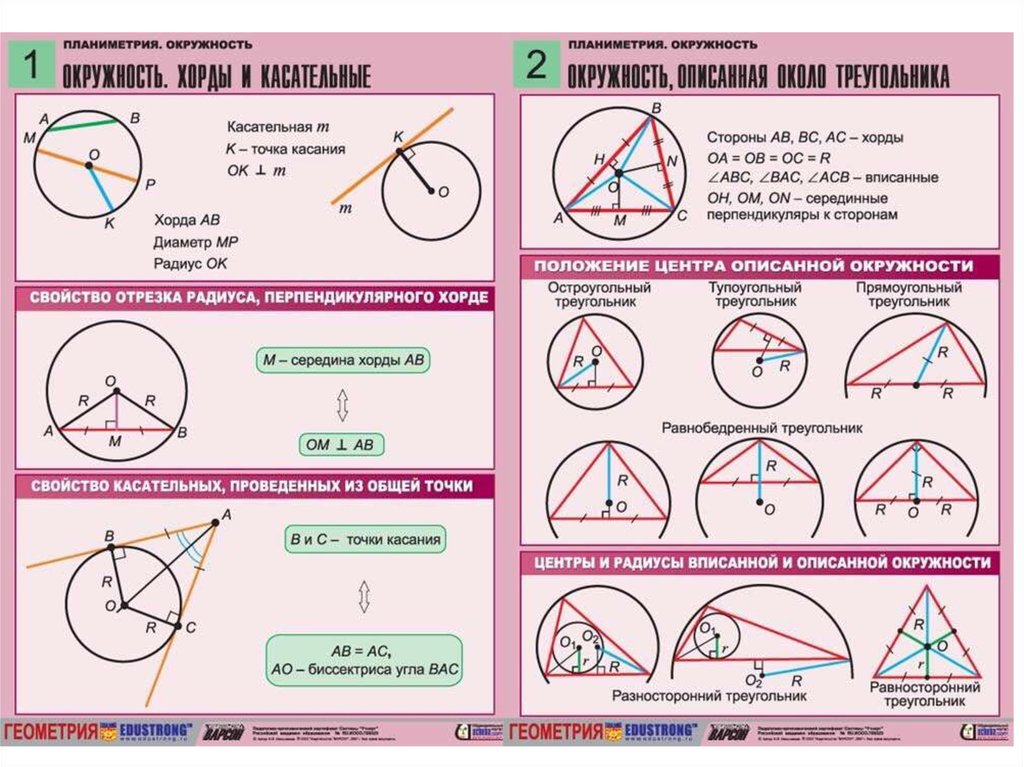 Рис. 1).

Рис. 1

Часть окруж­но­сти   на­зы­ва­ет­ся дугой.

Дуга имеет уг­ло­вое из­ме­ре­ние.

Гра­дус­ная мера дуги  равна гра­дус­ной мере со­от­вет­ству­ю­ще­го цен­траль­но­го угла :

Рас­смот­рим при­ме­ры:

Рис. 2

Опре­де­ле­ние

Угол, вер­ши­на ко­то­ро­го лежит на окруж­но­сти, а сто­ро­ны пе­ре­се­ка­ют окруж­ность, на­зы­ва­ет­ся впи­сан­ным.

 

Рис. 3

За­да­на окруж­ность с цен­тром О, вер­ши­на А лежит на окруж­но­сти, сто­ро­ны АВ и АС угла пе­ре­се­ка­ют окруж­ность в точ­ках В и С, угол  на­зы­ва­ет­ся впи­сан­ным. Он опи­ра­ет­ся на дугу , эта дуга рас­по­ло­же­на внут­ри угла (см. Рис. 3).

Впи­сан­ный угол из­ме­ря­ет­ся по­ло­ви­ной дуги, на ко­то­рую он опи­ра­ет­ся (см. Рис. 4).

Рис. 4

До­ка­за­тель­ство:

Рас­смот­рим несколь­ко слу­ча­ев.

          Слу­чай 1: точка О при­над­ле­жит лучу АС (см. Рис. 5).

Рис. 5

До­ка­зать, что 

Обо­зна­чим угол  через , тогда угол  также будет равен , так как тре­уголь­ник  рав­но­бед­рен­ный, его сто­ро­ны ОВ и ОА равны как ра­ди­у­сы окруж­но­сти. Угол  яв­ля­ет­ся внеш­ним для тре­уголь­ни­ка , внеш­ний угол равен сумме двух дру­гих углов, не смеж­ных с ним, по­лу­ча­ем: , то есть уг­ло­вое из­ме­ре­ние дуги  есть . Таким об­ра­зом, мы до­ка­за­ли, что впи­сан­ный угол равен по­ло­вине из­ме­ре­ния дуги, на ко­то­рую он опи­ра­ет­ся.

Слу­чай 2: точка О лежит внут­ри впи­сан­но­го угла  (см. Рис. 6).

Рис. 6

До­ка­зать, что 

До­ка­за­тель­ство сво­дит­ся к преды­ду­ще­му слу­чаю. Про­ве­дем диа­метр AD, обо­зна­чим угол  за  и тогда дуга  равна  (объ­яс­не­ние см. слу­чай 1). Угол  за , тогда дуга  равна  (объ­яс­не­ние см. слу­чай 1). Вся дуга  равна:

Угол  в свою оче­редь, равен .

Таким об­ра­зом, мы до­ка­за­ли, что впи­сан­ный угол равен по­ло­вине дуги, на ко­то­рую он опи­ра­ет­ся.

Слу­чай 3: точка О на­хо­дит­ся вне впи­сан­но­го угла (см.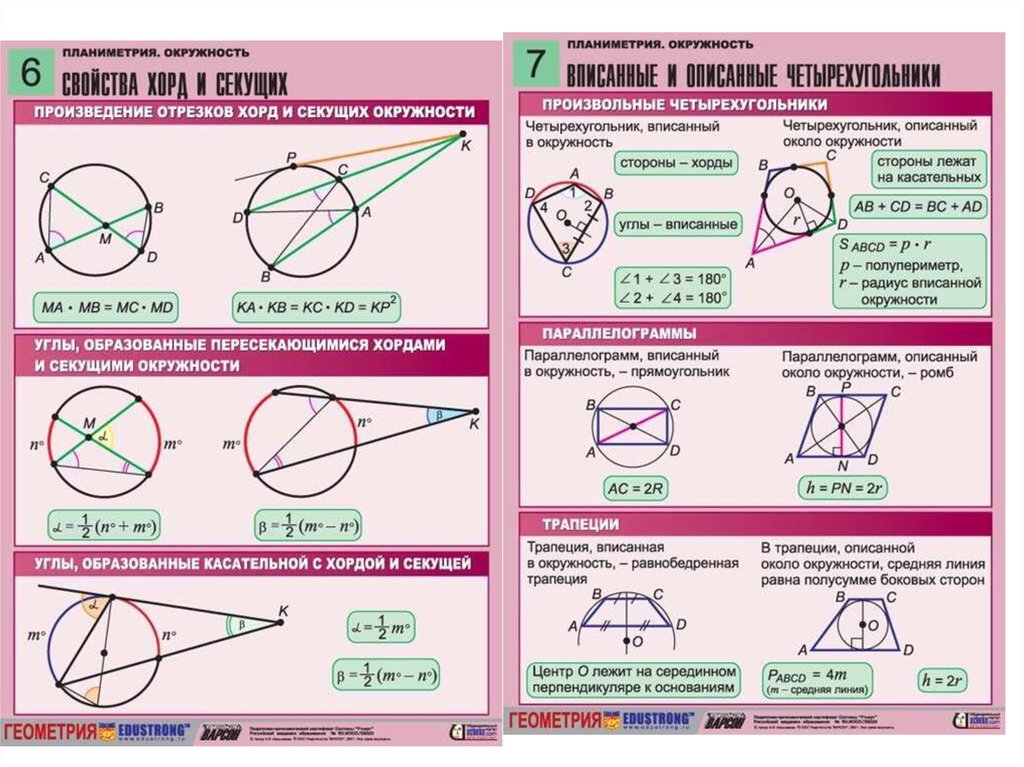 Рис. 7).

Рис. 7

До­ка­зать, что 

До­ка­за­тель­ство снова сво­дит­ся к пер­во­му слу­чаю. Про­ве­дем диа­метр AD, обо­зна­чим угол  через , тогда дуга  (объ­яс­не­ние см. слу­чай 1). Угол  обо­зна­чим через , тогда дуга  равна  (объ­яс­не­ние см. слу­чай 1). Дуга  яв­ля­ет­ся раз­но­стью боль­шой дуги  и дуги :

Впи­сан­ный угол  равен . Таким об­ра­зом, мы до­ка­за­ли, что впи­сан­ный угол равен по­ло­вине дуги, на ко­то­рую он опи­ра­ет­ся.

Итак, тео­ре­ма пол­но­стью до­ка­за­на, все слу­чаи рас­смот­ре­ны. И те­перь из этого вы­те­ка­ют важ­ные след­ствия.

След­ствие 1:

Впи­сан­ные углы, опи­ра­ю­щи­е­ся на одну и ту же дугу, равны между собой (см. Рис. 8).

Рис. 8

Угол  равен , он впи­сан­ный и опи­ра­ет­ся на дугу , зна­чит, дуга равна . Но на эту же дугу опи­ра­ют­ся много дру­гих углов, на­при­мер, углы  и , дан­ные углы из­ме­ря­ют­ся по­ло­ви­ной гра­дус­ной меры дуги, зна­чит, они равны , как и угол.

Таким об­ра­зом, по­лу­ча­ем:

След­ствие 2

Впи­сан­ные углы, опи­ра­ю­щи­е­ся на диа­метр, пря­мые (см. Рис. 9).

Рис. 9

Тео­ре­ма о впи­сан­ном угле яв­ля­ет­ся клю­чом к до­ка­за­тель­ству мно­гих дру­гих тео­рем и к ре­ше­нию мно­гих задач.

Про­из­ве­де­ние от­рез­ков каж­дой из двух пе­ре­се­ка­ю­щих­ся хорд есть ве­ли­чи­на по­сто­ян­ная.

Рис. 10

До­ка­зать, что 

До­ка­за­тель­ство:

Рас­смот­рим тре­уголь­ни­ки  и  (см. Рис. 10). Дан­ные тре­уголь­ни­ки по­доб­ны по ра­вен­ству двух углов: равны вер­ти­каль­ные углы  и ; впи­сан­ные углы  и  опи­ра­ют­ся на одну и ту же дугу . Вы­пи­шем со­от­но­ше­ние по­до­бия:

При­ме­ним свой­ство про­пор­ции и пре­об­ра­зу­ем вы­ра­же­ние:

, что и тре­бо­ва­лось до­ка­зать.

Итак, мы рас­смот­ре­ли по­ня­тие впи­сан­но­го угла и тео­ре­му о впи­сан­ном угле. В сле­ду­ю­щем уроке мы рас­смот­рим свой­ства бис­сек­три­сы угла и се­ре­дин­но­го пер­пен­ди­ку­ля­ра к от­рез­ку.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/okruzhnost/teorema-o-vpisannom-ugle

http://www.youtube.com/watch?v=v-udmw0gZIo

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/112-test-po-geometrii-8-klass-tema-tsentralnye-i-vpisannye-ugly-variant-1.html

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/113-test-po-geometrii-8-klass-tema-tsentralnye-i-vpisannye-ugly-variant-2.html

http://klassnoedelo.ru/upload/iblock/78d/78d9db552be4b537618cdef1c61fb4cd.jpg

 

Теоремы круга: откуда они берутся? — Блог MyTutor

На мой взгляд, самая важная фигура в математике — это круг. Его так просто понять, но он также дает нам одну из самых важных констант во всей математике: p. Как только мы нарисуем несколько линий внутри круга, мы сможем вывести закономерности и теоремы, полезные как в теоретическом, так и в практическом смысле. Определяющей чертой круга является его постоянный радиус, и я надеюсь показать вам, что, начиная с этой простой линии, мы можем вывести все теоремы о круге, которые вам нужно понять. Готовый? Пойдем.

Во-первых, мы должны знать, как построить равнобедренный треугольник из двух радиусов. Мы будем делать это часто, поэтому вот пример:

Поскольку все радиусы одинаковы, рисование двух радиусов образует треугольник с двумя равными сторонами — равнобедренный треугольник!

Теперь к теоремам:

1. Угол в центре вдвое больше угла на окружности

2. Угол в полуокружности прямой

3. Углы на одном отрезке равны

4. Сумма противоположных углов вписанного четырехугольника равна 180°

5. Угол между хордой и касательной равен углу на альтернативном отрезке

Найти репетитора 1. Угол в центре вдвое больше угла на окружности:

Как это показать? Начните с рисования линий, соединяющих A и D, B и C. Это образует три маленьких треугольника (∆ACD, ∆ABC, ∆ABD) и один большой (∆DCB). Поскольку все прямые AB, AC и AD являются радиусами окружности, это означает, что треугольники ∆ACD, ∆ABD и ∆ABC равнобедренные.

Итак, из ∆ABC мы можем видеть, что угол при A равен 180-2s (180° в треугольнике) .

И в большом треугольнике ∆DCB имеем:

(u+s)+(u+t)+(t+s) = 180° (180° в треугольнике) .

, который дает нам:

2U+2T+2S = 180 °

2U+2T = 180 ° -2S

= A

2. Угол в полукол.

Во-первых, мы можем видеть, что это приложение вышеприведенной теоремы с углом в центре = 180° . Если мы хотим показать это, не используя теорему 1, начнем с рисования линии от A до C. Обратите внимание, что это радиус окружности. Получаются три треугольника: ∆ABC, ∆ACD и большой ∆BCD. Имеем также, что ∆ABC и ∆ACD равнобедренные.

Во-первых, мы видим, что a+b=180° (180° по прямой) .

Для ∆ABC мы видим, что b+2s=180° (180° в треугольнике) . (1)

А для ∆ACD имеем a+2t=180° (180° в треугольнике) . (2)

Если сложить уравнения (1) и (2), получим b+2s+a+2t = 360°. Мы также знаем, что a+b=180°. Итак:

2s+2t+180° = 360°

2s+2t = 180°

s+t = 90°, чего мы и добивались.

 

3. Углы на одном отрезке равны:

Мы показываем это с помощью первой теоремы. Мы можем видеть, что, применяя первую теорему, мы получаем, что угол при С равен половине угла при А (в центре). Мы имеем, что угол при D также равен половине угла при A. Следовательно, угол при C равен углу при D.

 

4. Противолежащие углы в циклическом четырехугольнике суммируются до 180 °:

Угол при В + угол при D = угол при С + угол при Е равно 180° 900° четырехугольника четырехугольник, все углы которого лежат на окружности окружности.

Как и прежде, первым шагом будет проведение радиусов от центра к каждому углу четырехугольника. Это дает нам четыре равнобедренных треугольника: ∆ABC, ∆ACD, ∆ADE и ∆ABE.

Мы знаем, что сумма внутренних углов четырехугольника равна 360° (если вы не уверены в этом, подумайте о квадрате). Таким образом, мы видим:

Угол B    Угол C    Угол D      Угол E

(x+u) + (u+v) + (v+w) + (x+w) = 360°

2u + 2v + 2W + 2x = 360 °

U + V + W + X = 180 °

, поэтому мы имеем:

Угол B + Угол D

(U + X) + (V + W) = 180 °

и

Угол C    +     Угол E

(u + v)    +     (x + w) = 180°

 

5. альтернативный сегмент:

Наконец, одну из самых неожиданных теорем мы можем вывести, рисуя линии в кругах. Доказательство начинается таким же образом, проводя радиусы от центра окружности к каждой из точек B, C и D.

Это снова образует три равнобедренных треугольника: ∆ABC, ∆ABD и ∆ACD.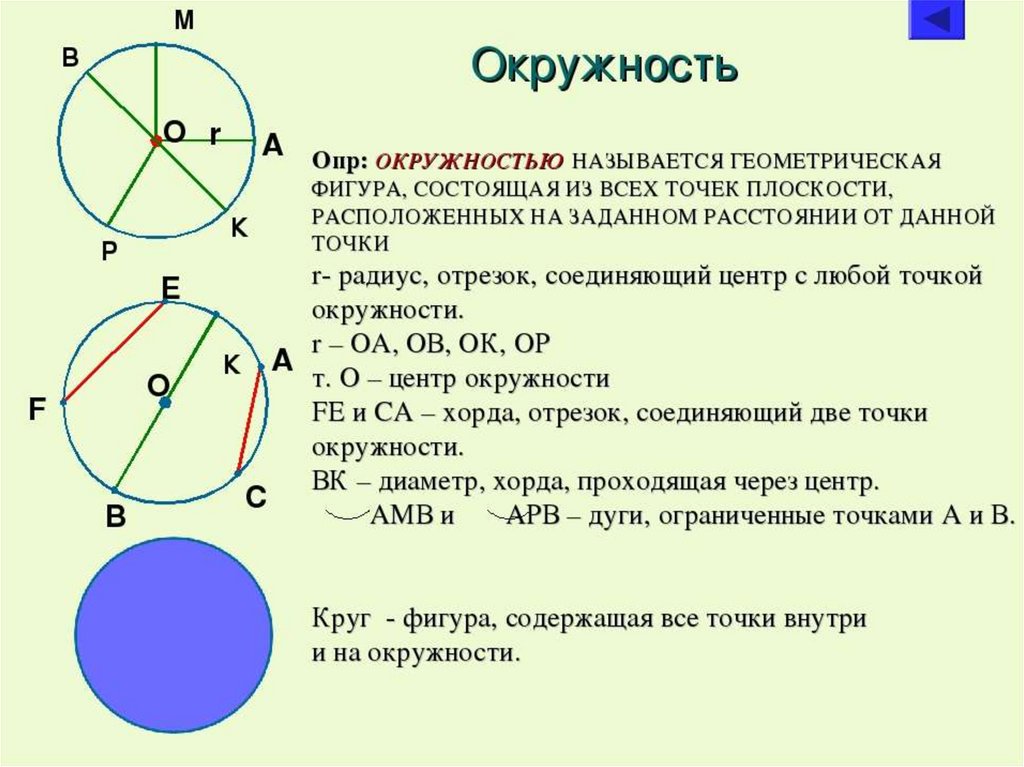

Мы хотим показать, что a = u+v.

В большем треугольнике ∆BCD мы знаем, что:

(u+w) + (v+w) + (u+v) = 180° (180° в треугольнике)

что приводит к:

2u + 2v + 2w = 180°

u + v + w = ​​90° (1)

Мы также знаем, что:

a = 90° – w (тангенс и радиус пересекаются под углом 90°)

Подставляя это в (1):

u + v = 90° – w

u + v = a, как требуется.

Я думаю, замечательно, что рисование простого радиуса может открыть нам внутри круга. Когда я изучал эти теоремы, я так и не понял, откуда они взялись, а теперь понимаете вы!

Помните, что, хотя вопросы могут показаться сложными, и может быть трудно определить, как получить ответ, уделение времени применению этих теорем значительно облегчит вашу работу. И если вам все еще нужна помощь, попробуйте индивидуальное объяснение от онлайн-репетитора по математике.

Крис Б. изучает математику и экономику в Университетском колледже Лондона. Он воодушевлен постоянной проблемой изучения математики и любит находить новые и интересные способы решения задач.

Теоремы о кругах — математика GCSE

Введение

Что такое теоремы круга?

Стяжные уголки

Теоремы круга рабочий лист

Распространенные заблуждения

Практические вопросы по теоремам круга

Круговые теоремы GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое теоремы круга?

Стяжные уголки

Рабочий лист теорем о кругах

Распространенные заблуждения

Практические вопросы по теоремам круга

Круговые теоремы GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о теоремах круга, включая их применение, доказательство и то, как их использовать для решения более сложных задач.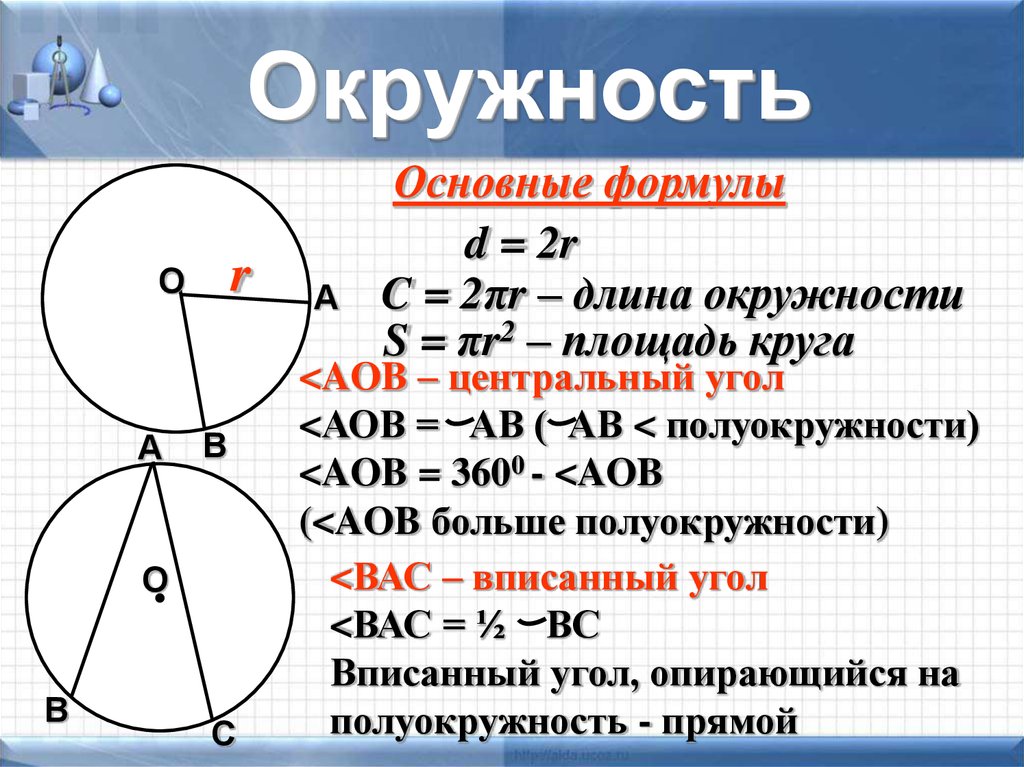

Существуют также рабочие листы с круговыми теоремами, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое теоремы о кругах?

Теоремы круга — это свойства, которые показывают отношения между углами в геометрии круга. Мы можем использовать эти теоремы вместе с предварительными знаниями о других свойствах углов для вычисления недостающих углов без использования транспортира. Это имеет очень полезные приложения в дизайне и инженерии.

Существует семь основных теорем о круге:

  1. Теорема об альтернативном сегменте круга
  2. Теорема об угле в центре окружности
  3. Углы в одном отрезке Теорема окружности
  4. Угол в теореме о полуокружности
  5. Теорема хордовой окружности
  6. Теорема касательной окружности
  7. Теорема о циклическом четырехугольнике

Ниже приводится краткое изложение каждой теоремы о круге вместе с диаграммой.

Вам нужно запомнить все эти правила теоремы о круге и уметь описать каждое из них в предложении.

Что такое теоремы о кругах?

Загрузите наш бесплатный плакат с теоремами о кругах, чтобы сосредоточить внимание на своей редакции!

Теорема о окружности 1: Альтернативный отрезок

Угол между касательной и хордой равен углу, образуемому той же хордой в альтернативном отрезке.

Пошаговое руководство: Теорема об альтернативных сегментах

Как использовать теорему об альтернативных сегментах

Чтобы использовать теорему об альтернативных сегментах

  1. Найдите ключевые части круга для теоремы.
  2. Используйте другие данные об углах, чтобы определить один из двух углов.
  3. Используйте теорему об альтернативных сегментах, чтобы установить другой недостающий угол.

Как использовать угол в центре теоремы

Чтобы использовать тот факт, что угол в центре вдвое больше угла на окружности

  1. Найдите ключевые части круга для теоремы.
  2. Используйте другие данные об углах, чтобы определить угол в центре или угол на окружности.
  3. Используйте угол в центре теоремы, чтобы определить другой недостающий угол.

Как использовать теорему об углах одного и того же сегмента

Чтобы использовать тот факт, что углы в одном и том же сегменте равны

  1. Найдите ключевые части круга для теоремы.
  2. Используйте другие данные об углах, чтобы определить угол на окружности в том же сегменте.
  3. Используйте угол из той же теоремы об отрезках, чтобы сформулировать другой отсутствующий угол.
    4. 9o

    1. Найдите ключевые части круга для теоремы.
    2. Используйте другие данные об углах, чтобы определить углы внутри треугольника.
    3. Используйте углы в теореме о полуокружности, чтобы сформулировать другой недостающий угол.

    Окружность Теорема 5: Хорда окружности

    Перпендикуляр из центра окружности к хорде делит хорду пополам (разделяет хорду на две равные части).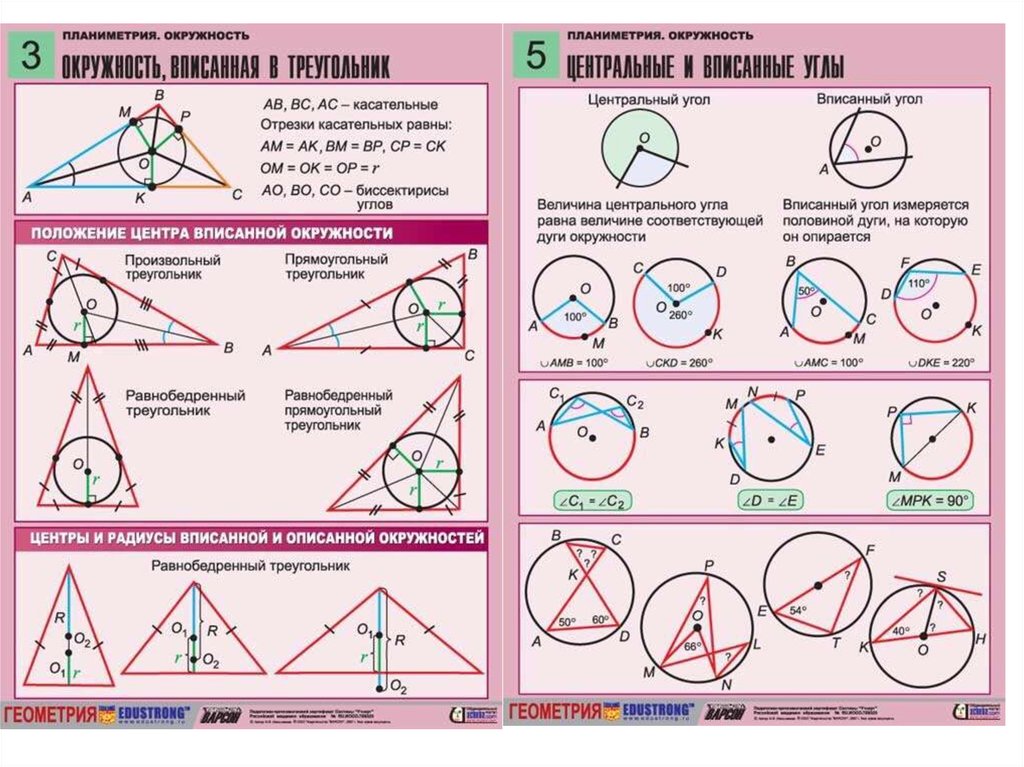

    Пошаговое руководство: Хорда окружности

    Как найти недостающие длины с помощью хорд

    Чтобы найти недостающие углы и длины с помощью хорд

    1. Найдите ключевые части окружности для соответствующей теоремы о окружности.
    2. Используйте другие данные об углах, чтобы определить недостающие углы.
    3. Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину.

    Круг Теорема 6: Тангенс окружности

    Угол между касательной и радиусом равен 90 градусов. Касательные, пересекающиеся в одной точке, имеют одинаковую длину.

    Диаграмма 1 Диаграмма 2

    Пошаговый руководство: Tangent of Circle

    Как использовать касательную теоремы круга

    . круга для теоремы.

  4. Используйте другие данные об углах, чтобы определить оставшиеся углы, образованные с касательной.
  5. Используйте теорему о касательной, чтобы установить другой недостающий угол.

Теорема об окружности 7: вписанный четырехугольник 9о

.

Пошаговое руководство: Вписанный четырехугольник

Как использовать теорему вписанного четырехугольника

Чтобы использовать теорему вписанного четырехугольника

  1. Найдите ключевые части круга для теоремы.
  2. Используйте другие данные об углах, чтобы определить один из двух противоположных углов в четырехугольнике.
  3. Используйте теорему о вписанном четырехугольнике, чтобы определить другой недостающий угол.

Сгибаемые уголки

Угол внутри окружности образуется двумя хордами, пересекающимися в одной точке на окружности. На приведенных ниже диаграммах показан угол, образуемый дугой AC из точки B для двух разных окружностей.

Полезный совет: слово «подтягивать» часто используется в теоремах о кругах, поэтому убедитесь, что вы знаете, что оно означает.

Пошаговое руководство: Сопрягаемые углы

Рабочий лист по теоремам об окружности

Получите бесплатный рабочий лист по теоремам об окружности, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист по теоремам о кругах

Получите бесплатный рабочий лист по теоремам о кругах, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Примеры теорем об окружности

Пример 1: теорема об альтернативных отрезках

Треугольник ABC вписан в окружность с центром O. Касательная DE пересекает окружность в точке A. Вычислите величину угла ABC.

    9о .


    Поскольку мы знаем сторону, прилегающую к углу, и хотим вычислить гипотенузу, нам нужно использовать \cos(\theta)=\frac{A}{H} с H в качестве подлежащего.


    \begin{выровнено} &H=\frac{A}{\cos(\theta)}\\\\ &x=\frac{5}{\cos(71)}\\\\ &x=15,4 см \; (1 дп) \end{aligned}

    Пример 6: касательная в теореме о окружности

    Точки A, B и C лежат на окружности с центром O. DE является касательной в точке A. Вычислите величину угла BAD. 9o

    • Разделение пополам и удвоение

    Неправильно запомнив теорему об угле в центре, учащийся удвоит угол в центре или половину угла на окружности.

    Главный совет: посмотрите на углы. Угол в центре всегда больше угла на окружности (это не так очевидно, когда угол на окружности находится в противоположном отрезке).

    • Углы одинаковые 9o когда связанная хорда не пересекает центр окружности и поэтому на диаграмме не изображен полукруг.

      • Параллельные прямые (теорема об альтернативных отрезках)

      Возьмем, к примеру, схему ниже:

      Предполагается, что хорда BC параллельна касательной, поэтому угол ABC равен углу при касательной. Здесь угол BCA был бы равен.

      Верхний совет: Используйте стрелки, чтобы визуализировать, как появляется альтернативный угол сегмента: 9о .

      • В теореме Пифагора отсутствует сторона

      Недостающая сторона вычисляется путем неправильного сложения квадрата гипотенузы и меньшей стороны, или путем вычитания квадрата меньшей стороны.

      • Неверная тригонометрическая функция

      Используется неверная тригонометрическая функция, поэтому вычисляемая сторона или угол неверны. Это также включает в себя обратные тригонометрические функции. 9о и треугольник равносторонний.

      (1)

      Учебный контрольный список

      Теперь вы узнали, как:

      • Применять и доказывать стандартные теоремы об углах, радиусах, касательных и хордах, а также использовать их для доказательства связанных результатов
        • 92571
      • застрявший?

        Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

        No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *