Найти асимптоты функции онлайн: Асимптоты функции онлайн

(2/3)

1. Вертикальные асимптоты.
2. Горизонтальные асимптоты.
3. Наклонные асимптоты.

Вертикальные асимптоты

Уравнение любой вертикальной прямой, то есть прямой, параллельной оси OY, имеет вид x=a. Если прямая x=a является вертикальной асимптотой графика функции y=f(x), то очевидно, что хотя бы один из односторонних пределов или равен бесконечности (+∞ или -∞).
Все функции с бесконечными разрывами (разрывы второго рода) имеют вертикальные асимптоты.

Пример 1. Найти уравнение вертикальных асимптот графика функции .
Решение. Видим, что y→∞, если x→1, точнее , , то есть прямая x=1 является вертикальной асимптотой, причем двусторонней.

Горизонтальные асимптоты

Всякая горизонтальная прямая имеет уравнение y=A.
Если прямая y=A является горизонтальной асимптотой кривой y=f(x), то .

Пример 2. Найти горизонтальные асимптоты кривой .
Решение. Найдем , то есть y→0 при x→+∞ и при x→-∞, значит прямая y=0 – горизонтальная асимптота данной кривой.

Наклонные асимптоты

Уравнения наклонных асимптот обычно ищут в виде y=kx+b. По определению асимптоты или (1)
Разделим обе части этого равенства на x: , откуда
(2)
Теперь из (1):
(3)
Для существования наклонных асимптот необходимо существование пределов (2) и (3). Если хотя бы один из них не существует, то наклонных асимптот нет. Пределы (2) и (3) нужно находить отдельно при x→+∞ и при x→-∞, так как пределы могут быть разными (функция имеет две разные асимптоты).

Пример 4. Найти наклонные асимптоты графика функции .
Решение. По формуле (2) найдем .
Теперь найдем . Получаем уравнение наклонной асимптоты

y=x+1.

Пример 5. Найти асимптоты кривой y=(x-1)2(x+3).
Решение. Вертикальных и горизонтальных асимптот нет, так как y→∞ при x→∞. Ищем наклонные:
.
Таким образом, кривая асимптот не имеет.

Пример 6. Найти асимптоты кривой .
Решение. Поскольку y→∞ при x→0 и при x→4, то прямые x=0 и x=4 являются вертикальными асимптотами. Так как , то y=2 – горизонтальная асимптота. Выясним вопрос о существовании наклонных асимптот: , следовательно, кривая наклонных асимптот не имеет (искать “b” не имеет смысла, так как горизонтальные асимптоты уже найдены).

Пример 7. Построить все виды асимптот к функции

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

Находим коэффициент k:

Находим коэффициент b:

Получаем уравнение наклонной асимптоты: y = -x
Найдем вертикальные асимптоты. Для этого определим точки разрыва:


Находим переделы в точке


— является вертикальной асимптотой.
Находим переделы в точке


— является вертикальной асимптотой.

Асимптоты графика функции, формулы и примеры решения задач

Содержание:

• Виды асимптот
• Нахождение наклонной асимптоты

Виды асимптот

Определение

Прямая $x=x_{0}$ называется вертикальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $\lim _{x \rightarrow x_{0}-0} f(x)$ или $\lim _{x \rightarrow x_{0}+0} f(x)$ равно $+\infty$ или $-\infty$ .

Замечание. Прямая $x=x_{0}$ не может быть вертикальной асимптотой, если функция непрерывна в точке $x=x_{0}$ . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.

Определение

Прямая $y=y_{0}$ называется горизонтальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $\lim _{x \rightarrow+\infty} f(x)$ или $\lim _{x \rightarrow-\infty} f(x)$ равно $y_{0}$ .

Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.

Определение

Прямая $y=k x+b$ называется наклонной асимптотой графика функции $y=f(x)$, если $\lim _{x \rightarrow \infty}[f(x)-k x-b]=0$

Нахождение наклонной асимптоты

Теорема

(условиях существования наклонной асимптоты)

Если для функции $y=f(x)$ существуют пределы $\lim _{x \rightarrow \infty} \frac{f(x)}{x}=k$ и $\lim _{x \rightarrow \infty}[f(x)-k x]=b$, то функция имеет наклонную асимптоту $y=k x+b$ при $x \rightarrow \infty$ .

Замечание

Горизонтальная асимптота является частным случаем наклонной при $k=0$ .

Замечание

Если при нахождении горизонтальной асимптоты получается, что $\lim _{x \rightarrow \infty} f(x)=\infty$, то функция может иметь наклонную асимптоту.

Замечание

Кривая $y=f(x)$ может пересекать свою асимптоту, причем неоднократно. {2}-x}{x+1}=\lim _{x \rightarrow \infty} \frac{-4 x+2}{x+1}=-4$

Таким образом, наклонная асимптота: $y=x-4$ .

Ответ. Вертикальная асимптота — прямая $x=-1$ .

Наклонная асимптота — прямая $y=x-4$ .

Читать дальше: исследование функции и построение ее графика.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Калькулятор асимптот — онлайн-поиск по горизонтали/вертикали/наклону

Поиск инструмента

Поиск инструмента в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Асимптота функции

Инструмент для поиска уравнений асимптот (горизонтальных, вертикальных, наклонных или изогнутых) функции или математического выражения.

Результаты

Асимптота функции — dCode

Теги: Функции

Поделиться

dCode и другие

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор асимптот

Функция $ f(x)= $
Переменная
Поиск горизонтальной асимптоты в плюс бесконечность ($ x \to + \infty $)
Поиск горизонтальной асимптоты в минус бесконечность ($ x \to — \infty $)
Поиск вертикальной асимптота
Поиск косой/наклонной или криволинейной асимптоты

См. также: Предел функции — Область определения функции

Проверка асимптот

Функция $ f(x)= $
Переменная

Проверка вертикальной асимптоты

Абсцисса где $х\до$

Проверка на аффинную/наклонную/наклонную асимптоту

Асимптотическая функция $ g(x)= $

См. также: Предел функции — область определения функции

Ответы на вопросы (FAQ)

Что такое асимптота? (Определение)

Асимптота — это линия (или иногда кривая), стремящаяся (аналогично касательной) к функции на бесконечности.

Как найти горизонтальную асимптоту?

Функция $ f(x) $ имеет горизонтальную асимптоту $ y = a $ if

$$ \lim\limits_{x \rightarrow +\infty} f(x)=a $$ и/или $ $ \lim\limits_{x \rightarrow -\infty} f(x)=a $$

Для нахождения горизонтальной асимптоты вычисление этого предела является достаточным условием.

Пример: $ 1/x $ имеет для асимптоту $ y=0 $, потому что $ \lim\limits_{x \rightarrow \infty} 1/x = 0 $

Не может быть более 2 горизонтальных асимптот .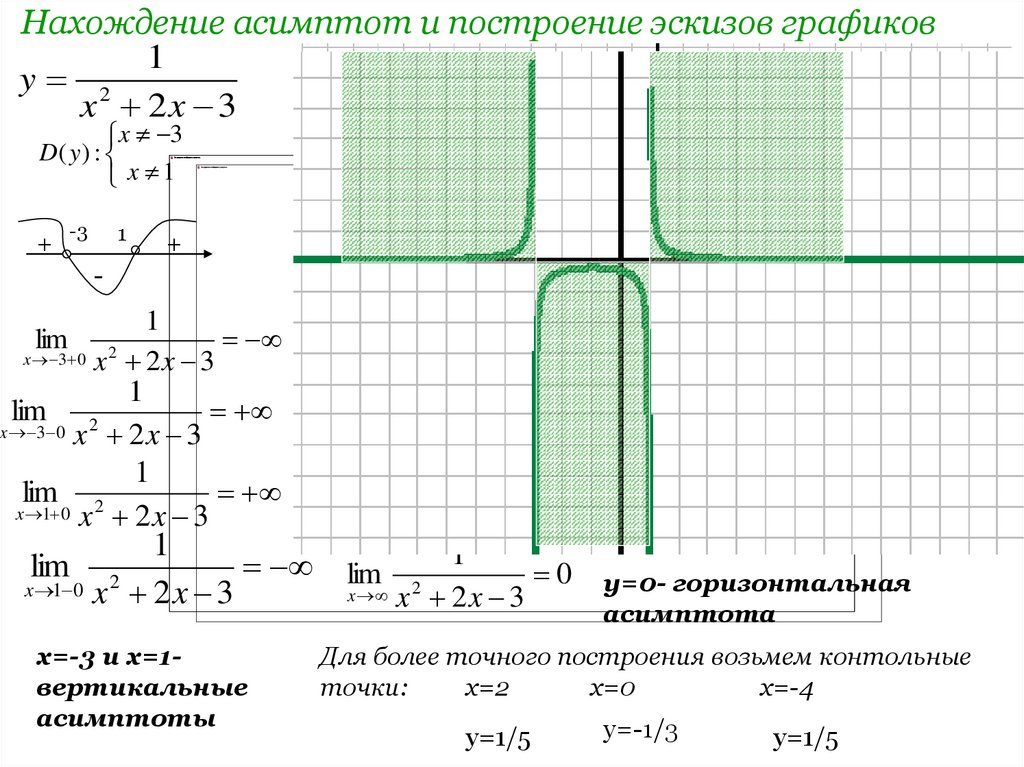

Как найти вертикальную асимптоту?

Функция $f(x)$ имеет вертикальную асимптоту $x = a$, если она допускает бесконечный предел в $a$ ($f$ стремится к бесконечности).

$$ \lim\limits_{x \rightarrow \pm a} f(x)=\pm \infty $$

Чтобы найти горизонтальную асимптоту расчет этого предела является достаточным условием.

Пример: $ 1/x $ имеет для асимптоту $ x=0 $, потому что $ \lim\limits_{x \rightarrow 0} 1/x = \infty $

Обычно функция не определена в $ a $ необходимо проанализировать область определения функции, чтобы найти потенциальные асимптоты .

Вертикальных асимптот может быть бесконечное количество.

Для рациональной функции (с дробью: числитель над знаменателем) значения, у которых знаменатель равен нулю, равны асимптоты .

Как найти наклонную/наклонную асимптоту?

Функция $ f(x) $ имеет наклонную асимптоту $ g(x)=ax+b $, когда

$$ \lim\limits_{x \rightarrow \pm \infty} \left( f(x )-g(x)= 0 \right) $$

Вычисление наклона асимптоты можно упростить, вычислив этот предел:

$$ \lim\limits_{x \rightarrow \pm \infty} \left( \ frac{f(x)}{g(x)} = 1 \right) $$

Для рациональной функции применение полиномиального деления позволяет найти косую асимптота .

Как найти нелинейную асимптоту?

Функция $ f(x) $ имеет нелинейную асимптоту $ g(x) $ при

$$ \lim\limits_{x \rightarrow \pm \infty} \left( f(x)- g(x)= 0 \right) $$

Метод аналогичен вычислению наклонной асимптоты .

Исходный код

dCode сохраняет за собой право собственности на исходный код «Асимптоты функции». За исключением явной лицензии с открытым исходным кодом (указывается Creative Commons/бесплатно), алгоритма «Асимптота функции», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Асимптота функций» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанных на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Асимптоты функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!

Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Асимптота функции» или любых ее результатов разрешена, если вы цитируете dCode!
Бесплатный экспорт результатов в виде файла .csv или .txt осуществляется нажатием на значок экспорта -22, https://www.dcode.fr/asymptote-функция

Резюме

• Калькулятор асимптот
• Проверка асимптот
• Что такое асимптота? (Определение)
• Как найти горизонтальную асимптоту?
• Как найти вертикальную асимптоту?
• Как найти наклонную/наклонную асимптоту?
• Как найти нелинейную асимптоту?

Похожие страницы

• Предел функции
• Область определения функции
• Касательная к кривой
• Степень полинома
• Функция ошибки
• Область производной функции
• Логарифм
• СПИСОК ИНСТРУМЕНТОВ DCODE

Поддержка

• Paypal
Patreon

 

Форум/Помощь

Ключевые слова

асимптота, функция , бесконечность, вертикаль, горизонталь, наклон, наклон

Ссылки

▲

Калькулятор асимптот — онлайн-калькулятор асимптот

Прямая линия называется асимптотой кривой y = f (x), если, говоря простым языком, кривая касается линии на бесконечности.

Что такое калькулятор асимптот?

«Калькулятор асимптот Cuemath» — это онлайн-инструмент, который помогает рассчитать асимптотический график для заданной функции. Калькулятор асимптот Cuemath поможет вам найти асимптотический график для заданной функции за несколько секунд.

Как пользоваться калькулятором асимптот?

Чтобы использовать калькулятор, выполните следующие действия:

• Шаг 1: Введите функцию относительно одной переменной в заданных полях ввода.
• Шаг 2: Нажмите кнопку «Вычислить» , чтобы найти асимптотический график для заданной функции
• Шаг 3:  Нажмите кнопку  «Сброс» , чтобы очистить поля и найти асимптотический график для различных функций.

 

Как найти асимптоты?

Асимптота определяется как линия, к которой приближается кривая, но не пересекает ее бесконечно, или можно сказать, что асимптота — это линия, к которой сходится кривая. Асимптота никогда не пересекает кривую, даже если они бесконечно близки.

Существует три типа асимптот: 1. Горизонтальная асимптота 2. Вертикальная асимптота 3. Наклонная асимптота

1. Горизонтальная асимптота: функции.

• Если оба многочлена имеют одинаковую степень, разделите коэффициенты членов с наибольшими степенями. Это ваша асимптота!
• Если степень числителя меньше знаменателя, то асимптота расположена при y=0.
• Если степень числителя больше знаменателя, то горизонтальной асимптоты нет!

2.Вертикальная асимптота: Вертикальная асимптота встречается в рациональных функциях в точках, когда знаменатель равен нулю, а числитель не равен нулю. Мы можем найти вертикальную асимптоту, приравняв знаменатель рациональной функции к нулю.

 

Хотите находить сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.

No related posts.