1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол . С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений. 2. К тригонометрическим функциям относятся следующие 6 функций: синус , косинус , тангенс ,котангенс , секанс и косеканс . Для каждой из указанных функций существует обратная тригонометрическая функция. 3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга . 4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: 5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: 6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: 7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: 8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): 9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): 10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Синусом угла α называется отношение противолежащего катета к гипотенузе. Косинусом угла α называется отношение прилежащего катета к гипотенузе. Тангенсом угла α называется противолежащего катета к прилежащему. Котангенсом угла α называется прилежащего катета к противолежащему. Секанс угла α представляет собой отношение гипотенузы к прилежащему катету. Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету. 11. График функции синус 12. График функции косинус 13. y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞ 14. График функции котангенс 15. | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Радианная мера угла. Синус, косинус, тангенс числа
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
 Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Радианная мера угла.
Синус, косинус, тангенс числа.
Тригономе́трия (от греч. τρίγονο (треугольник) и греч.
μετρειν (измерять),
то есть измерение треугольников) — раздел математики,
в котором изучаются тригонометрические функции и их
приложения к геометрии.
Данный термин впервые появился в 1595 г. как название
книги немецкого математика Бартоломеуса Питискуса
(Bartholomäus Pitiscus, 1561—1613),
расчётов в астрономии, геодезии и архитектуре.
Эти ученые внесли свой вклад в развитие тригонометрии
Архимед
Жозеф Луи
Лагранж
Фалес
Тригонометрия возникла и развивалась в древности как
один из разделов астрономии, как ее вычислительный
аппарат, отвечающий практическим нуждам человека.
 С ее
С еепомощью можно определить расстояние до недоступных
предметов и существенно упрощать процесс геодезической
съемки местности для составления географических карт.
Общепринятые понятия тригонометрии, а также
обозначения и определения тригонометрических функция
сформировались в процессе долгого исторического развития.
Тригонометрические сведения были известны древним
вавилонянам и египтянам, но основы этой науки заложены в
Древней Греции встречающиеся уже в III веке до н.э.
Апполония Пергского. Древнегреческие астрономы успешно
решали вопросы из тригонометрии, связанные с астрономией.
Соотношение между сторонами и углами
прямоугольного треугольника
0 90
с
а
в
a
sin
ñ
b
cos
c
a
tg
b
b
ñtg
a
Синус/ Косинус острого угла в прямоугольном треугольнике
—
отношение противолежащего/прилежащего катета к гипотенузе.

Тангенс/Котангенс— отношение противолежащего/прилежащего
катета к прилежащему/противолежащему.
В XVIII веке Леонард Эйлер
дал современные, более
общие определения,
расширив область
определения этих функций
на всю числовую ось.
угол _ поворота
R
у
1
0
х
1
у
1
0
х
1
Рассмотрим в прямоугольной системе координат
окружность единичного радиуса и отложим от
горизонтальной оси угол
(если величина угла положительна, то откладываем против
часовой стрелки, иначе по часовой стрелке). Точку
пересечения построенной стороны угла с окружностью
у
обозначим Р.
0
Р
1
0
1
х
1
0
Р90
у
Р60
Р45
Р30
Р180
Р
1
0
х 0
1
Р360
Ð 30
Р270
у
Р45
Ð405
1
0
х
1
360 0 ,
ãäå 0, 1, 2,…
360 0 45 4050
Вспомните как расположены четверти в прямоугольной
системе координат и запишите соответствие градусных
мер в каждой четверти.

Центральный угол, опирающийся на дугу, длина которой равна радиусу
окружности, называется углом в 1 радиан.
в градусах
π
1º = —— рад
180
где π ≈ 3,14
в радианах
180º
1 рад = ——
π
1 радиан ≈ 57,3º:
у1
cos
P ( x; y )
у
P0 (1;0)
1
0
1
sin
х
х
1
cos x
sinопределяется
yкак ордината
Синус угла
точки P
Косинус — абсцисса точки P
y
ординаты к абсциссе
Тангенс –tg
отношение
точкиxP
x
Котангенсctg
– отношение
точки
абсциссы к ординате
Py
Р90
Ð120
у
Р0 (1; 0)
Ð60
Р90 (0; 1)
у
Ð60 (x; y)
Р180
Р
1
-х
0
х 0
1
х
Р360
Ð120 (-x; y)
Р180 (-1; 0)
Р270
Р270 (0;-1)
Градусы
0°
30°
45°
60°
90°
120°
135°
150°
180°
270°
360°
Радианы
0
π/6
π/4
π/3
π/2
2π/3
3π/4
5π/6
π
3π/2
2π
sin а
0
1/2
√2/2
√3/2
1
√3/2
√2/2
1/2
0
-1
0
сos a
1
√3/2
√2/2
1/2
0
-1/2
-√2/2
-√3/2
-1
0
1
tg a
0
√3/3
1
√3
—
-√3
-1
-√3/3
0
—
0
ctg a
—
√3
1
√3/3
0
-√3/3
-1
-√3
—
0
—
Свойства тригонометрических функций
Знаки синуса, косинуса, тангенса, котангенса в координатных четвертях
у
у
+ +
х
1
— —
0
1
— +
+ 1
1
х
— +
+ 1
1
0
sin68 0
cos 76 0
sin 153 0
cos 236 0
sin 249 0
tg127 0
sin 315 0
ctg195 0
у
0
— +
— +
1
1
0
у
х
х
Четность, нечетность синуса, косинуса, тангенса, котангенса
sin( ) sin
tg ( ) tg
Нечетные функции
ctg ( ) ctg
cos( ) cos
Четная функция
Периодичность тригонометрических функций
При изменении угла на целое число оборотов
значения синуса, косинуса, тангенса, котангенса
не изменяются
sin( 2n ) sin
2
cos( 2n ) cos
2
tg ( ) tg
ctg ( ) ctg
08.

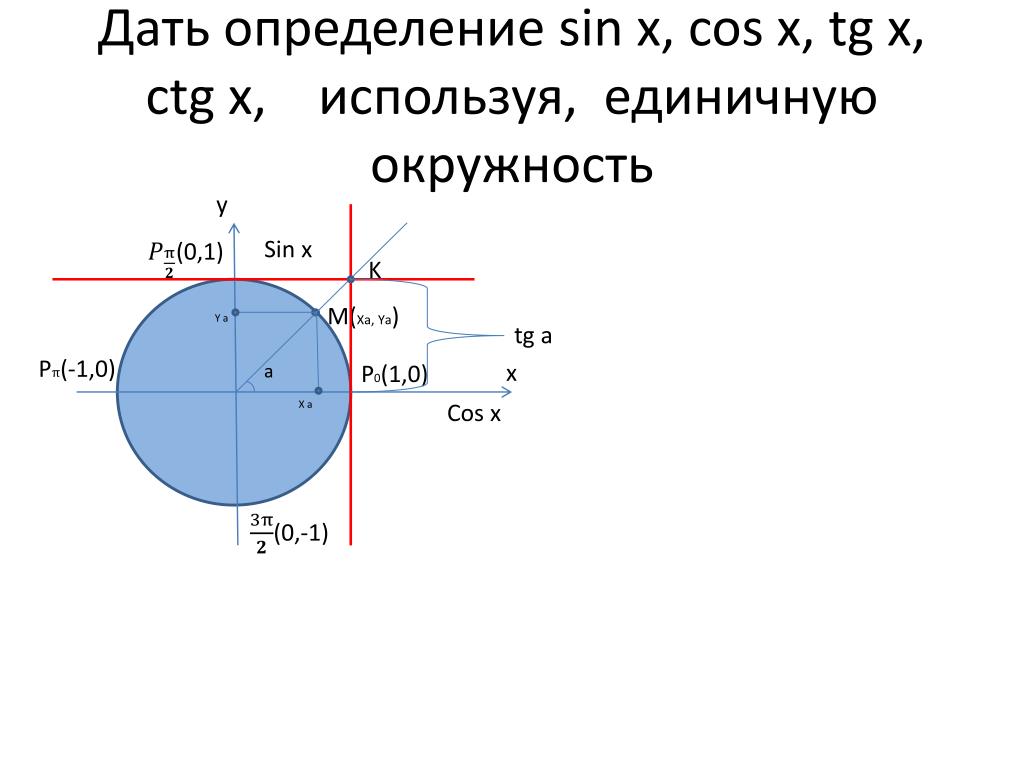
 На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
 График функции секанс
График функции секанс  Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.