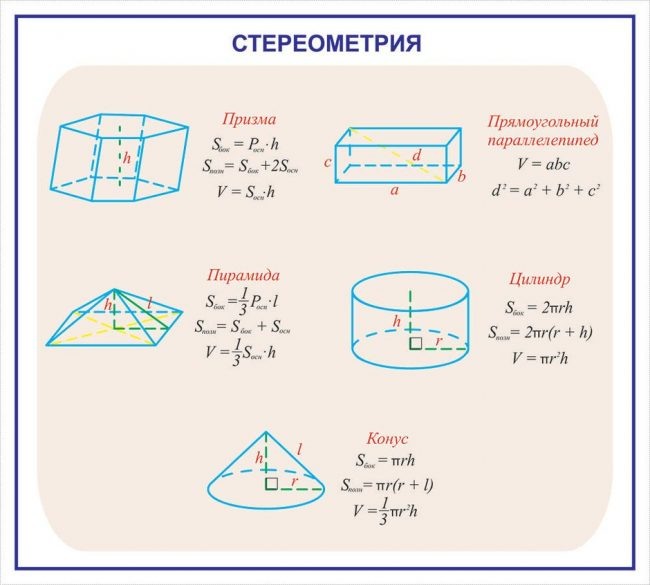
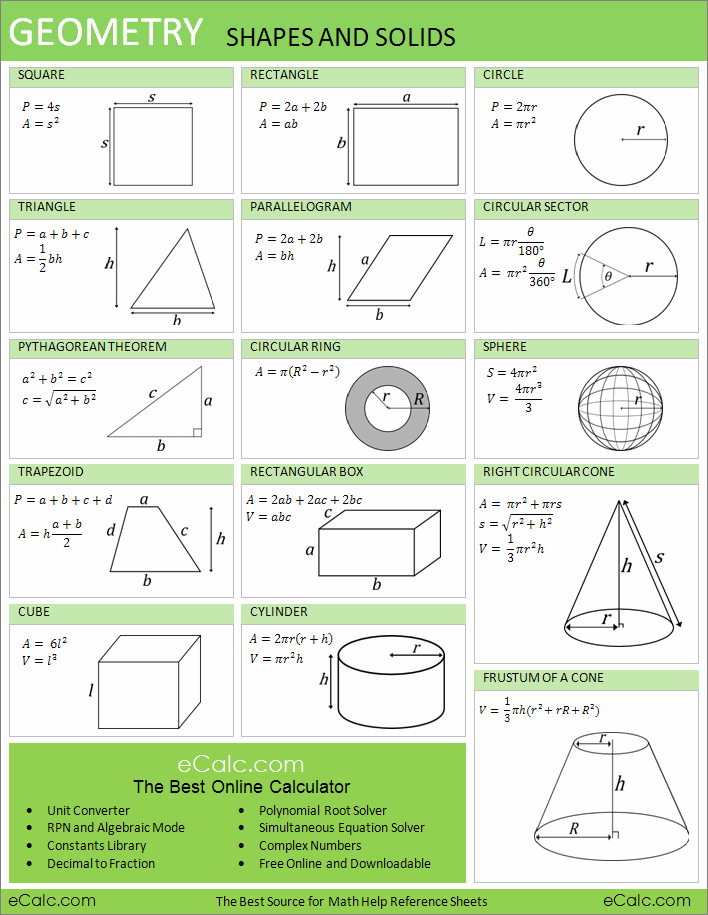
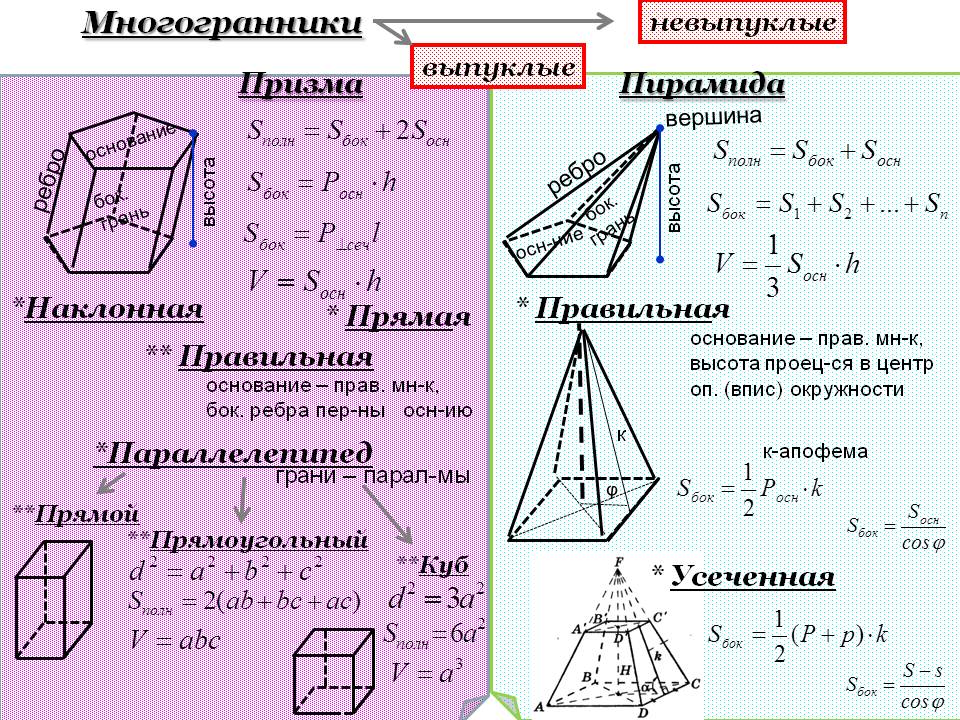
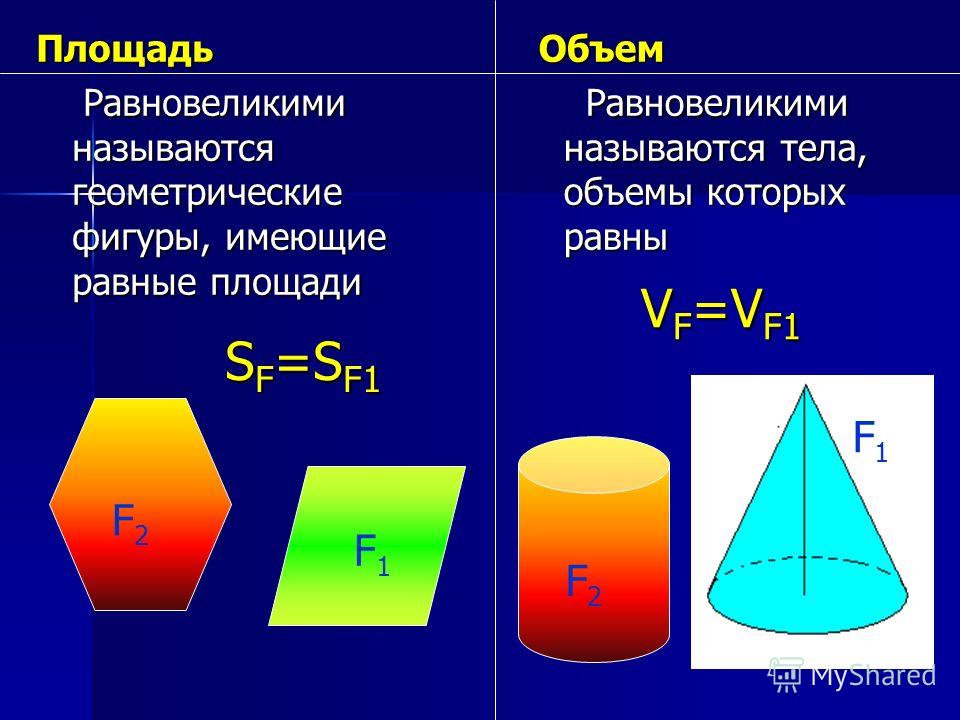
Объемы и площади: Объем, Площадь поверхности, формулы объема

Объемы и площади поверхностей усеченных пирамид и конусов.

Навигация по справочнику TehTab.ru:  главная страница / / Техническая информация/ / Математический справочник/ / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Объемы и площади поверхностей усеченных пирамид и конусов.

Объемы и площади поверхностей усеченных пирамид и конусов. Усеченная пирамида или конус — это часть, остающаяся после отсечения вершины плоскостью, параллельной основанию. Объем усеченной пирамиды или конуса равен объему целой пирамиды или конуса минус объем отсеченной вершины. Площадь боковой поверхности усеченной пирамиды или конуса равна площади поверхности целой пирамиды или конуса. минус площадь боковой поверхности отсеченной вершины. Если необходимо найти общую площадь усеченной фигуры, тогда площадь двух параллельных оснований добавляется к площади боковой поверхности. Существует и другой метод определения объема и площади поверхности усеченного конуса:   V=1/3 π h(R2+Rr+r2), площадь боковой поверхности конуса S=π l(R+r), общая площадь поверхности Sо=π l(R+r)+πr2+πR2               Пример1. Определение площади необходимого для изготовления материала для абажура. (Расчет площади боковой поверхности конуса). Абажур имеет форму усеченного конуса. Высота абажура равна 50 см, нижний и верхний диаметры — 40 и 20 см соответственно. Определить с точностью до 3х значащих цифр площадь материала, необходимого для изготовления абажура. Как было определено выше, площадь боковой поверхности усеченного конуса S=π l(R+r). Поскольку верхний и нижний диаметры усеченного конуса равны 40 и 20 см, то из рис. выше находим r=10 см, R=20 см и l=(50 2+102)1/2=50,99 согласно теореме Пифагора, Следовательно, площадь боковой поверхности конуса равна S=π 50,99(20+10)=4803,258 см2, т.е. площадь необходимого для изготовления абажура материала равняется 4800 см2 с точностью до 3х значащих цифр, хотя, конечно, сколько на самом деле уйдет материала зависит от кроя.   Пример 2. Определение объема цилидра, увенчанного усеченным конусом. Башенный охладитель имеет форму цилиндра, увенчанного усеченным конусом, как показано на рис. ниже. Определить объем воздушного пространства в башне, если 40 % объема занято трубами и другими структурами. Объем цилиндрической части V=π R2h=π(27/2)2*14=8011,71 м3 Объем усеченного конуса V=1/3 π h(R2+Rr+r2), где h=34-14=20 м, R=27/2=13,5 м и r=14/2=7 м. Т.к. R=27/2=13,5 м и r=14/2=7 м. Следовательно, объем усеченного конуса V=1/3 π 20(13,52+13,5*7+72)=6819,03 м3 Общий объем башенного охладителя V общ. =6819,03+8011,71=14830,74 м3. Если 40% объема занято, объем воздушного пространства V=0,6*14830,74=8898,44 м3

Дополнительная информация от TehTab.ru:

Площади и объёмы — Электронные учебники по математике

Скорость это физическая величина, показывающая, какое расстояние пройдет объект за единицу времени. Скорость90 км/ч. обозначает, что объект за один час преодолеет 90 км. Давайте напишем формулу скорости. Формула это математическая запись, в которой величины представлены в виде общепринятых букв (переменных). Скорость — V Путь — S Время — t Исходя из этого, формула скорости будет выглядеть так: V = S : t Применим эту формулу для решения следующей задачи. Машина, двигаясь равномерно (с постоянной скоростью) за два часа прошла 120 км. С какой скоростью двигалась машина? V = S : t = 120 : 2 = 60 км/ч. Мы подставили в формулу пройденное расстояние (путь) и время за которое оно было пройдено, и нашли скорость. V = 60 км/ч.

Теперь, исходя из формулы скорости, напишем формулу пути. S = V • t Решим задачу. Поезд двигался равномерно 3 часа со скоростью 50 километров в час. Какой путь прошел поезд за это время? S = V • t = 50 • 3 = 150 км. Используя формулу пути, мы нашли ответ. Поезд за 3 часа прошел 150 километров. Длина это величина характеризующая размер какого — нибудь отрезка на прямой, а площадь это величина показывающая размер той части плоскости, которая очерчена соединенными между собой отрезками (смотри рисунок). Принято, что площадь квадрата со сторонами равными 1 тоже равна 1. Если стороны измерены в метрах то площадь будет измеряться в м2, если в см то и площадь в см2. Площадь трех квадратов (закрашенных голубым) со сторонами 1см будет равна 3 см2 . Площадь девяти квадратов (закрашенных зеленым) со сторонами 1см будет равна 9 см2 . На рисунке хорошо видно, что для нахождения площади нам надо найти, сколько единичных квадратов умещается в нашем прямоугольнике, а для этого надо умножить длину на ширину. a — длина; b — ширина; S — площадь; S = a • b . Прямоугольник — это четырехугольник со всеми прямыми углами. Квадрат — прямоугольник, у которого все стороны равны. Площадь фигуры — это сумма площадей фигур, из которых она состоит. Перечислим единицы измерения площади: квадратный миллиметр (мм2) , квадратный сантиметр (см2) , квадратный дециметр (дм2) , квадратный метр (м2) , квадратный километр (км2) , гектар (га) , ар (a) (сотка) . Площадь квадрата со сторонами 1м равна один квадратный метр, а квадрата со сторонами 1мм равна один квадратный миллиметр. Площадь квадрата со сторонами 100м равна один гектар. Этой единицей площади пользуются для измерения площади земли. Так как, 1га равен 100м • 100м , то 1га = 10 000м2 . Так же площадь полей и земли измеряют в арах (а). Ар (сотка) равен квадрату со сторонами 10м . Значит, 1а = 100 м2. 1 дм = 10 см, в 1дм2 содержится 10см • 10см , значит 1дм2 = 100см2 . Таким же образом получаем, что 1м2 = 100дм2, 1м2 = 10 000см2 и 1см2 = 100мм2. У прямоугольников, у которых длина и ширина выражена в метрах, площадь считают в квадратных метрах. Если же длина и ширина прямоугольника записана в разных единицах, то их надо привести, к одной единице измерения длины. На рисунке изображен прямоугольный параллелепипед. В жизни мы сталкиваемся с такой формой в виде коробка спичек, коробки из-под обуви, кирпича и т.д. Прямоугольники, составляющие поверхность параллелепипеда, называются гранями. У параллелепипеда их 6, причем грани расположенные напротив друг друга равны. У параллелепипеда есть 12 ребер, они также являются сторонами граней. Точки схождения ребер называются вершинами параллелепипеда. Площадь грани 1 изображенной на рисунке равна произведению первого и второго ребра. Площадь всей поверхности параллелепипеда равна сумме площадей граней 1, 2 и 3умноженной на 2. 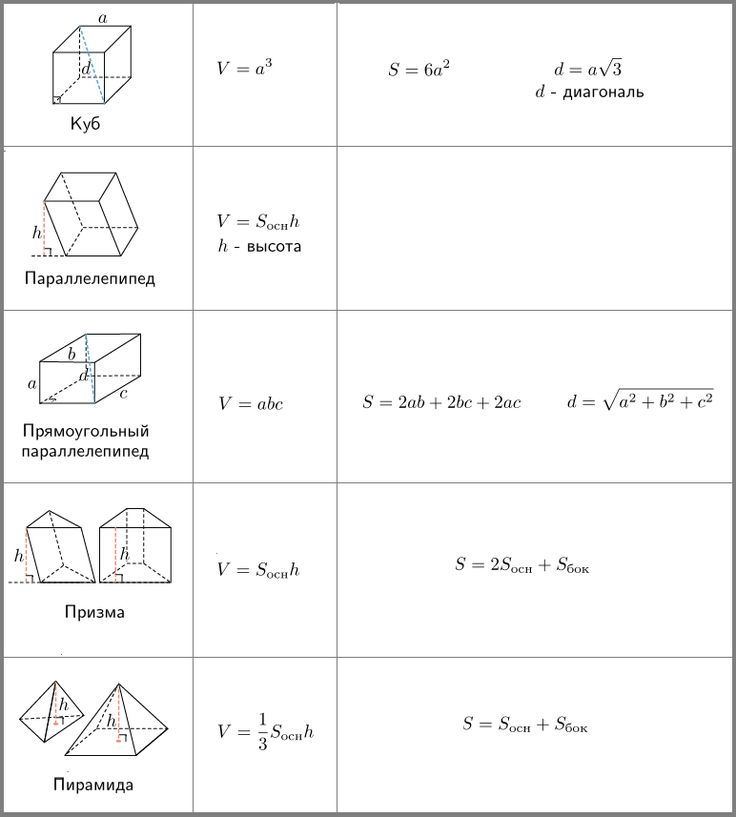Прямоугольный параллелепипед определяется тремя измерениями. Высота (обозначим буквой h) равна длине ребра № 1. Длина (обозначим буквой m) равна длине ребра № 2. Ширина (обозначим буквой n) равна длине ребра № 3. Если площадь всей поверхности параллелепипеда обозначить буквой S, то формула ее нахождения будет выглядеть так: S = (h • m + h • n + n • m) • 2 Кубом называют прямоугольный параллелепипед, у которого все измерения равны. Поверхность куба составляет 6 равных квадрата. Если длину ребра куба обозначить буквой n, то площадь одной грани S = n2 Прямоугольный параллелепипед обладает еще одним измерением, которое называется объем (обозначим буквой V) . V = h • m • n Величина объем показывает, какую часть пространства занимает объект. В быту объем чаще всего используется для измерения жидкостей, и самая распространенная единица измерения объема является литр = 1дм3. Так же для измерения объема используются м3, мм3, см3, км3. Куб с размерами 1см будет обладать объемом 1 см3. V = 1 см • 1 см • 1 см = 1 см3. Два таких куба вместе займут вдвое больший объем 2 см3, то есть объем объекта это сумма объемов фигур, из которых состоит объект.

 

Проверь себя!!!                                                                     Контроль знаний

 

1.Из приведённых ниже равенств выберите формулу для нахождения скорости.

a) S = ab;
б) s = vt;
в) v = s/t ;
г) t = s/v .

2. Выберите из предложенных равенств формулу вычисления площади квадрата.

а) S = ab ;
б) S = aа ;
в) S = 2ab;
г) S = 4a.

3. Длина доски равна 2м 5 дм 6см 4мм. Выразите данную длину в миллиметрах.

а) 20 564 мм;
б) 2 564 мм;
в) 25 064 мм;
г) 250 604 мм.

4. Выразите в квадратных метрах 15 га 7 а.

а) 150 700 м2;
б) 15 700 м2;
в) 15 070 м2;
г) 1 507 000 м2.

5. Периметр квадрата 48 дм. Найдите его площадь.

а) 12 дм;
б) 12 дм2;
в) 144 дм;
г) 144 дм2.

6. Ширина прямоугольника 130 м, а длина на 70 м больше. Найдите площадь данного прямоугольника в арах.

а) 260 а;
б) 26 а;
в) 2 600 а;
г) 26 000 а

7. Найдите сторону прямоугольника, если его площадь 60 см2, а другая сторона равна 12 см.

а) 5 см;
б) 720 см;
в) 3 см;
г) 6 см.

8. Найдите объём прямоугольного параллелепипеда, если его стороны 15 дм, 4 м и 20см

а) 1 200 000 м3;
б) 1 200 дм3;
в) 120 м3;
г) 12 м3

9.Найдите высоту прямоугольного параллелепипеда, если его объём равен 240 см3, длина 6 см, ширина 8 см.

а) 5см;
б) 6см;
в) 3см;
г) 50 см.

10. Вычислите общую длину всех рёбер прямоугольного параллелепипеда, если его
измерения 32 дм, 56 дм, 43 дм.

а) 262 дм;
б) 131 дм;
в) 786дм;
г) 524 дм.

11. Кирпич имеет длину 25 см, ширину 12 см и толщину 7 см. Камаз с прицепом привёз на стройку 42 м3 кирпича. Найдите число кирпичей, доставленных на стройку.

а) 2000;
б)200;
в) 20 000;
г) 20.

12. Объём одного прямоугольного параллелепипеда равен 12 дм3. Чему равен объём другого параллелепипеда, если его длина в 9 раз больше, ширина в 4 раза больше, а высота в 6 раз меньше первого?

а) 72 дм3;
б) 54 дм3;
в) 48 дм3;
г) 36 дм3.

Разница между площадью и объемом

Площадь определяется как область, покрытая объектом, тогда как объем определяется как емкость объекта. Площадь рассчитывается для двумерного объекта, тогда как объем рассчитывается для трехмерного объекта. Площадь связана с внешним пространством, а объем с внутренней емкостью. Площадь измеряется в квадратных единицах, таких как квадратные дюймы, квадратные футы и т. д., а объем измеряется в кубических единицах, таких как кубические футы, кубические дюймы и т. д.

В этой статье давайте рассмотрим разницу между площадью и объемом с помощью решенных примеров и практических вопросов.

1.	Что такое площадь и объем?
2.	Разница между площадью и объемом
3.	Формулы площади и объема
4.	примеров разницы между площадью и объемом
5.	Часто задаваемые вопросы о разнице между площадью и объемом

Что такое площадь и объем?

Площадь

Площадь относится к объему пространства, занимаемому двухмерной фигурой/объектом. Другими словами, это величина, измеряющая количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Стандартной единицей площади являются квадратные единицы, обычно представленные как квадратные дюймы, квадратные футы и т. д.

Объем

Объем относится к мере емкости, которую может удерживать объект. Его также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов.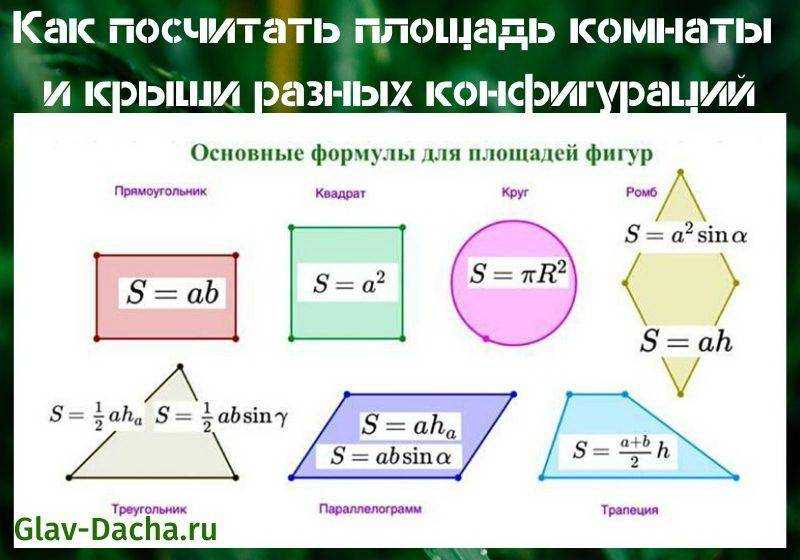 Стандартной единицей площади являются кубические единицы, обычно представленные в кубических дюймах, кубических футах и ​​т. д.

Разница между площадью и объемом

Важные различия между площадью и объемом перечислены в таблице ниже.

Площадь по сравнению с объемом

Площадь	Том
Площадь всегда определяется для двухмерных объектов или плоских фигур.	Объем всегда определяется для трехмерных объектов или объемных фигур.
Измеряется в двух измерениях, включая в основном длину и ширину.	Измеряется в трех измерениях, включая третье измерение, то есть высоту.
Измеряется в квадратных единицах	Измеряется в кубических единицах
Область охватывает внешнее пространство объекта.	Объем — это емкость объекта.

Формулы площади и объема

Формулы площади и объема для различных двумерных и трехмерных форм приведены в таблицах, приведенных ниже.

Таблица формул площади для 2D-фигур

Геометрические фигуры	Формула площади
Квадрат	A = a 2 (a = сторона квадрата)
Прямоугольник	A = l × w (l = длина, w = ширина)
Треугольник	A = ½ x b x h (b = основание, h = высота)
Параллелограмм	A = b × h (b = основание, h = высота по вертикали)
Ромб	A = a × h (a = сторона ромба, h = высота)
Круг	A = π r 2 (r = радиус окружности)
Полукруг	A = π r 2 (r = радиус окружности)
Трапеция	A = ½ (a + b)h (a = основание 1, b = основание 2, h = высота по вертикали)

Таблица формул объема для трехмерных фигур

Геометрические фигуры	Формула объема
Куб	V = a 3 (a = сторона квадрата)
Прямоугольный	V = l × w × h (l = длина, w = ширина, h = высота)
Правый круглый конус	V = 1/3 (π r 2 h) (r = радиус круглого основания, h = высота конуса)
Правый круговой цилиндр	V = π r 2 h (r = радиус круглого основания, h = высота цилиндра)
Правая пирамида	V = 1/3 (площадь основания) × высота
Правая призма	V = площадь основания × высота
Сфера	V = 4/3 (π r 3 ) (r = радиус сферы)
Полусфера	В = 2/3 (π r 3 ) (r = радиус полушария)

Статьи по теме

Посмотрите еще несколько интересных статей, основанных на разнице между площадью и объемом.

• Формы
• Твердые формы
• Геометрия
• Площадь квадрата
• Площадь прямоугольника
• Объем конуса
• Объем куба
• Объем прямоугольного параллелепипеда

 

Примеры разницы между площадью и объемом

1. Пример 1: Размеры прямоугольника 10 см и 8 см. Найдите его площадь.

   Решение :

   Площадь прямоугольника равна произведению его длины на ширину, что можно представить по формуле: Площадь = l × w.
   Подставляя данные значения, получаем площадь прямоугольника = 10 × 8 = 80 см ²
   Следовательно, площадь прямоугольника равна 80 см ²

2. Пример 2: Определите объем конического сосуда с радиусом 7 дюймов и высотой 9 дюймов. Используйте π = 22/7.

   Решение:

   Сосуд имеет форму конуса.
   Объем конуса = 1/3 π r² h = 1/3 × 22/7 × 7 × 7 × 9 = 462 дюйма ³ .
   Следовательно, объем сосуда равен 462 в ³ .

перейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы о разнице между площадью и объемом

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о разнице между площадью и объемом

В чем разница между площадью и объемом?

Важные точки различия между площадью и объемом.

• Площадь определяется как область, охватываемая объектом, тогда как объем определяется как емкость объекта.
• Площадь рассчитывается для двухмерного объекта, тогда как объем рассчитывается для трехмерного объекта.
• Площадь измеряется в квадратных единицах, а объем измеряется в кубических единицах.

В чем разница между площадью, периметром и объемом?

Площадь относится к пространству, занимаемому формой, тогда как периметр относится к расстоянию вокруг формы (граница формы), а объем относится к емкости данной трехмерной формы.

Как площадь связана с объемом?

Площадь поверхности — это в основном площадь объекта, выставленная наружу, тогда как объем — это пространство внутри формы.

Какова площадь треугольника?

Площадь треугольника — это общее пространство, занимаемое тремя его сторонами в двумерной плоскости. Формула площади треугольника равна половине произведения его основания на высоту, т. е. A = 1/2 × b × h. он применим ко всем типам треугольников — разносторонним треугольникам, равнобедренным треугольникам или равносторонним треугольникам. Обратите внимание, что в случае треугольника основание и высота перпендикулярны друг другу.

Как найти площадь круга?

Площадью круга называется пространство, занимаемое кругом на двумерной плоскости.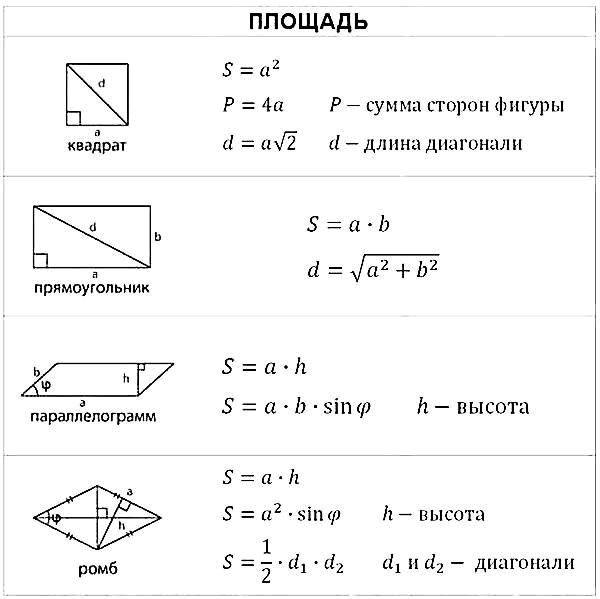 Другими словами, это пространство, занимаемое в пределах границы круга. Формула площади круга: A = πr ² , где r — радиус круга. Единицей площади является квадратная единица, например, м ² , см ² , дюймы ² и т. д.

Что такое объем цилиндра?

Объем цилиндра относится к пространству, занимаемому цилиндром в трехмерной плоскости. Формула площади цилиндра: A = πr ² h, где «r» — радиус основания (окружности) цилиндра, «h» — высота цилиндра, а π — константа, значение которой равно 22/7 (или) 3,142. Он измеряется в кубических единицах, таких как см ³ , м ³ , дюймы ³ и т. д.

Площади поверхности и объемы — GeeksforGeeks

Можно измерить три измерения: длину, ширину и высоту, для любого объект, который вы можете увидеть или потрогать. Есть определенные размеры нашего дома, в котором мы живем. Прямоугольный экран/монитор, на который вы смотрите, имеет ширину и ширину, равные его собственной длине.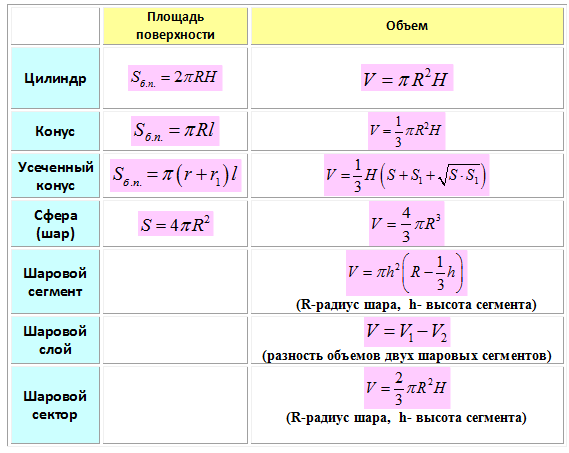 Для каждой трехмерной геометрической структуры измеряются площадь поверхности и объем.

Площадь или зона, покрываемая поверхностью объекта, — это площадь поверхности любого данного объекта. Принимая во внимание, что количество пространства, доступного в объекте, является объемом.

Площадь поверхности

Площадь поверхности и объем можно рассчитать для любой трехмерной (3D) геометрической формы. Поверхность любой области – это область, занятая поверхностью объекта. Объем — это объем доступного пространства в объекте. У нас есть различные типы форм, такие как полусфера, сфера, куб, прямоугольный параллелепипед, цилиндр и т. д. Все трехмерные формы имеют площадь и объем. А вот двухмерные формы, такие как квадрат, прямоугольник, треугольник, круг и т. д. Здесь в двухмерном пространстве мы можем измерить только площадь. Площадь, занимаемая трехмерным объектом его внешней поверхностью, называется площадью поверхности. Измеряется в квадратных единицах.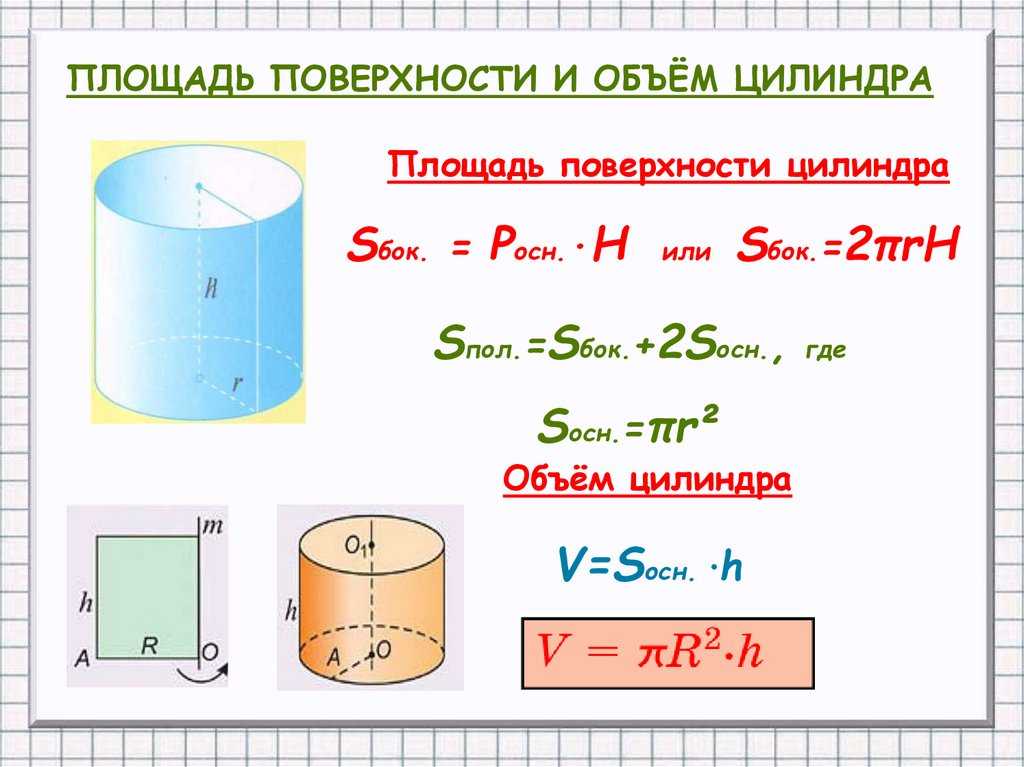

Площадь бывает двух типов:

1. Общая площадь поверхности
2. Площадь изогнутой поверхности/площадь боковой поверхности

Общая площадь поверхности

Площадь, включая основание(я) и изогнутую часть, соответствует общей площади поверхности . Это площадь, ограниченная поверхностью объекта. Если форма имеет изогнутое основание и поверхность, то сумма двух областей будет общей площадью. Общая площадь поверхности может быть определена как «общая площадь, покрытая объектом, включая его основание, а также изогнутую часть. Если у объекта есть и площадь основания, и площадь кривизны, то общая площадь поверхности будет равна сумме площади основания и площади кривизны».

• Общая площадь поверхности — это общая площадь, занимаемая объектом.
• Например, прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин.

Общая площадь поверхности = Площадь основания + Площадь кривизны

• Сумма всех этих 6 площадей будет нашей общей площадью поверхности конкретной формы

является прямоугольным параллелепипедом, длина которого равна 8 см, ширина = 4 см и высота = 6 см, найдите TSA прямоугольного параллелепипеда

дано l = 8см, b = 4см, h = 6см + (8 * 6) + (4 * 6))

= 2((32) + (48) + (24))

= 2(104)

= 208

TSA прямоугольного параллелепипеда составляет 208см .

Площадь криволинейной поверхности/Площадь боковой поверхности

Площадь криволинейной поверхности, за исключением ее центра, соответствует площади только изогнутой части формы (форм). Для таких форм, как конус, ее часто называют площадью боковой поверхности. Площадь боковой поверхности можно определить как «площадь, которая включает только площадь криволинейной поверхности объекта или площадь боковой поверхности объекта, исключая базовую площадь объекта». Площадь боковой поверхности также известна как площадь криволинейной поверхности. Большинство форм или объектов относятся к области изогнутой поверхности, форма или объект, подобный цилиндру, относятся к ней как к области боковой поверхности. Проще говоря, «Область, которую мы видим, называется боковой поверхностью». Например, рассмотрим цилиндр, как показано на рисунке ниже.

Объем

Объем — это объем пространства в определенном трехмерном объекте. Общее количество пространства, которое занимает объект или вещество, называется объемом. Измеряется в кубических единицах.

Формулы площади поверхности и объема

В приведенной таблице указаны общая площадь поверхности, площадь криволинейной поверхности/площадь боковой поверхности и объем различных форм.

Название формы	Curved Surface Area	Total Surface Area	Volume
Cuboid	2h(l + b)	2(lb + bh + hl)	л * б * в
Куб	4a 2	6a 9020 2	a 3
Cylinder	2πrh	2πr(r + h)	πr 2 h
Sphere	4πr 2	4πr 2	4/3π r 3
Cone	πrl	πr(r + l)	1/3π r 2 h
Hemisphere	2πr 2	3πr 2	2/ 3π r 3

Примеры

Пример 1: 2 куба объемом 512 см каждый ³ соединены встык. Найдите площадь поверхности получившегося прямоугольного параллелепипеда?

Решение:

Учитывая,

Объем (V) каждого куба равен = 512 см ³

теперь мы можем предположить, что ³ = 512 см ³

3 9, т. a = 8 см

Теперь ширина и длина полученного прямоугольного параллелепипеда будут равны 8 см каждый, а его высота будет равна 16 см.

Итак, площадь поверхности прямоугольного параллелепипеда (TSA) = 2(lb + bh + lh)

Теперь, подставляя значения, получаем

= 2(8 × 16 + 8 × 8 + 16 × 8) см ²

= (2 × 320) = 640 см ²

Следовательно, TSA из кубоида = 640 CM ²

9000 2 6. см в диаметре и длиной 2 см. Плавится в виде прямоугольной свечи размером 7 см × 11 см × 1 см. Сколько кубовидных свечей можно получить?

Решение:

Размеры цилиндрической свечи:

Радиус цилиндрической свечи = 14/2 см = 7 см

Высота/Толщина = 2 см

Объем одной цилиндрической свечи = πr ² h = π x 7 x 7 x (2) см ³ = 308 см ³ .

Объем кубовидной свечи = 7 x 11 x 1 = 77 см ³

Следовательно, количество кубовидных свечей = Объем кубовидной свечи/Объем одной цилиндрической свечи = 308/77 = 4

Отсюда получаем 4 свечи кубической формы.

Пример 3: Женщина хочет построить сферический игрушечный шар из глины, радиус которого равен радиусу браслета, который она носит. Учитывая, что браслет имеет круглую форму, она также хочет, чтобы площадь браслета равнялась объему сферы. Узнать радиус браслета, который она носит?

Решение:

Пусть r будет радиусом как браслета, так и сферы,

Нам дано, что объем сферы равен площади браслета:

Следовательно,

πr ² = 4/3 πr ³

⇒ r = 3/4

Следовательно, радиус браслета равен 3/4 единицы.

Пример 4: Дана высота наклона прямого круглого конуса 25 см, а его высота 24 см. Найдите площадь криволинейной поверхности конуса?

Решение:

Формула площади криволинейной поверхности конуса: πrl. Где r — радиус конуса, а l — наклонная высота конуса.

Здесь конус — правый круговой конус.

Таким образом, радиус конуса будет:

=> 

=> r = 7 см.

Теперь расчет криволинейной поверхности:

Требуемая площадь = (22/7) * 7 * 25 = 550 см ²

Отсюда площадь криволинейной поверхности конуса равна 550 см ² .

Пример 5: Найдите площадь боковой поверхности цилиндра с радиусом основания 6 дюймов и высотой 14 дюймов.

Решение:

Данный радиус R = 6, высота H = 14

LSA = 2∏RH

= 2 * ∏ * 6 * 14

= 168∏

= 527,787

= 168∏

= 527,787

= 168∏

= 527,787

= 168∏

= = 528.

No related posts.