Что такое диаметр окружности. Площадь круга
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге.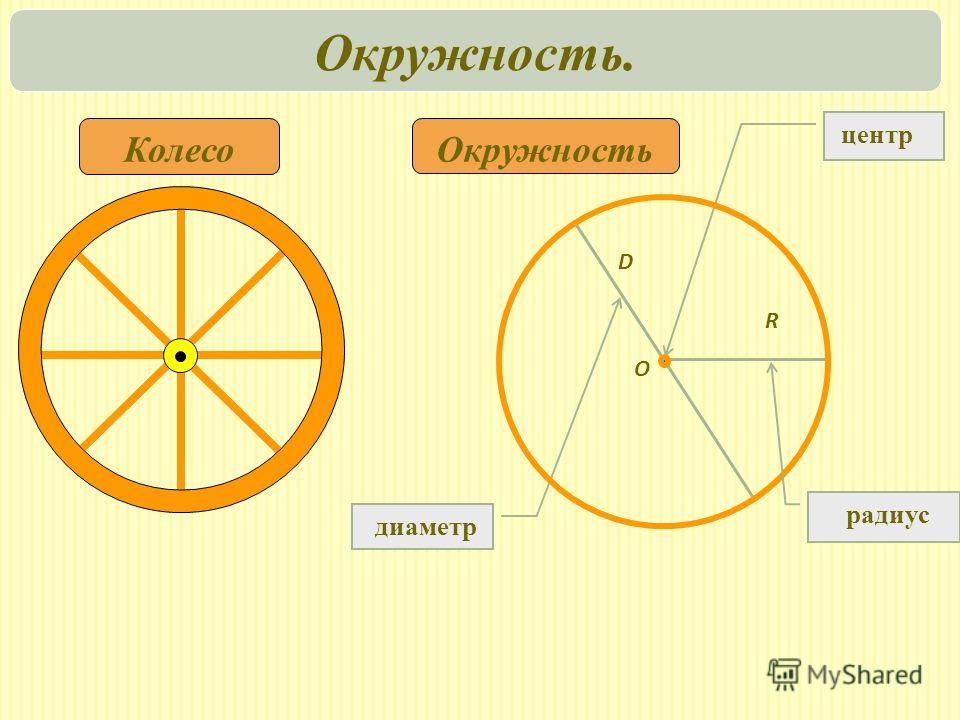 В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.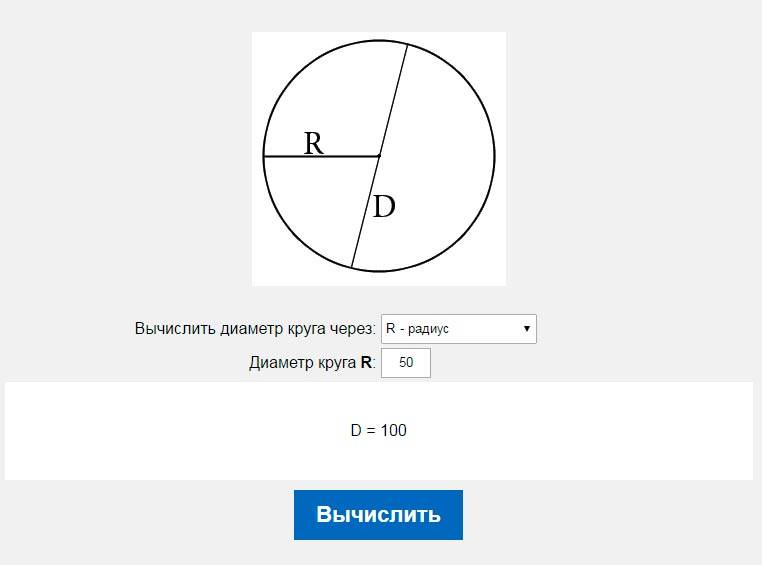
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов
и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a
ее можно найти по теореме Пифагора: отсюда .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Если в задаче известны такие величины, как длина окружности, ее радиус или площадь круга, который ограничен данной окружностью, то вычисление диаметра будет несложным. Существует несколько способов, которыми можно высчитать диаметр окружности. Они довольно просты и вовсе не вызывают никаких трудностей, как многим кажется на первый взгляд.
Существует несколько способов, которыми можно высчитать диаметр окружности. Они довольно просты и вовсе не вызывают никаких трудностей, как многим кажется на первый взгляд.
Как найти диаметр окружности – 1 способ
Когда дано значение радиуса окружности, то можно считать задачу наполовину решенной, поскольку радиус представляет собой расстояние от точки, которая лежит в любом месте на окружности, до центра этой самой окружности. Все, что нужно сделать для нахождения диаметра в этом случае, это умножить данную величину радиуса на 2. Такой способ вычисления объясняется тем, что радиус является половиной диаметра. Поэтому, если известно, чему равен радиус, то и значение половины искомой величины диаметра уже фактически найдено.
Как найти диаметр окружности – 2 способ
Если в задаче дано только значение длины окружности, то для нахождения величины диаметра нужно просто поделить ее на число, известное как π, приблизительное значение которого равно 3,14. То есть, если значение длины равняется 31,4, то разделив его на 3,14, получаем значение диаметра, которое равняется 10.
Как найти диаметр окружности – 3 способ
Если в исходных данных приведено значение площади круга, то диаметр найти тоже просто. Все, что нужно сделать, это извлечь квадратный корень из данной величины и поделить полученный результат на число π. Это значит, что если значение площади равно 64, то при извлечении корня остается число 8. Если разделить полученную 8 на 3,14, то получим величину диаметра, которая равна примерно 2,5.
Как найти диаметр окружности – 4 способ
Внутри окружности нужно начертить при помощи линейки или угольника прямую горизонтальную линию от одной точки до другой. Пересечения этой прямой с линией окружностью пометьте буквами, например, А и В. Не имеет никакого значения, в какой из частей круга будет расположена эта прямая.
После этого нужно начертить еще две окружности. Но таким образом, чтобы точки А и В стали их центрами. Вновь образованные фигуры будут пересекаться в двух точках. Через них нужно провести еще одну прямую линию. После этого измеряем ее длину с помощью линейки.
Интересно, что еще очень далеко в прошлом для плетения корзин определенного размера прутики брали примерно в 3 раза длиннее. Ученые объяснили и доказали экспериментальным путем, что если длину любой окружности разделить на диаметр, то в результате получается почти одно и то же число.
И круг — геометрические фигуры, взаимосвязанные между собой. есть граничная ломаная линия (кривая) круга ,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R ).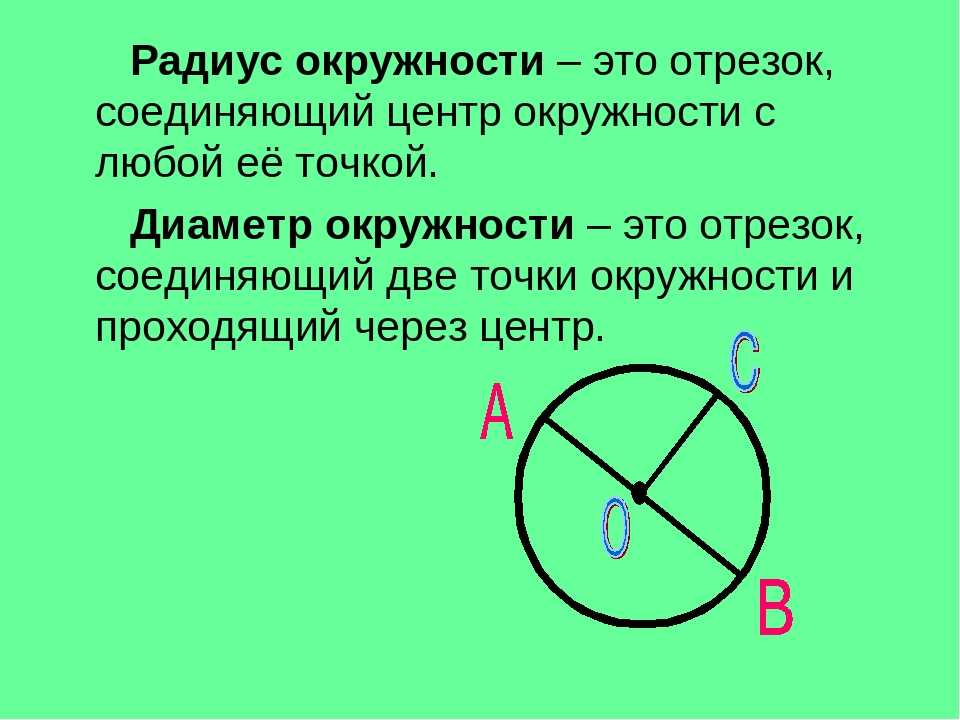 Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов , лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D ).
Правило. Диаметр окружности равен двум ее радиусам .
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C ). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.
- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.

- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой , уменьшается по мере удаления секущей от центра окружности.
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S ) равна произведению квадрата радиуса (r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами . Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
Как найти радиус окружности — Лайфхакер
20 февраля 2020ЛикбезОбразование
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Поделиться
0Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Сейчас читают 🔥
- ТЕСТ: Сможете ли вы решить простейшие уравнения?
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
Иллюстрация: Лайфхакер- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
Иллюстрация: Лайфхакер- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.

- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
как замерить по длине окружности, измерить рулеткой, определить диаметр
Содержание:
Определение диаметра в бытовых условиях
Измерение диаметров в производственных условиях
В процессе выполнения строительных работ в быту или на производстве может появиться необходимость в измерении диаметра трубы, которая уже вмонтирована в систему водоснабжения или канализации. Также знать данный параметр необходимо на стадии проектирования прокладки инженерных коммуникаций.
Также знать данный параметр необходимо на стадии проектирования прокладки инженерных коммуникаций.
Отсюда возникает необходимость разобраться с тем, как определить диаметр трубы. Выбор конкретного способа выполнения измерений зависит от размеров объекта и от того, доступно ли расположение трубопровода.
Определение диаметра в бытовых условиях
До того как замерить диаметр трубы, нужно приготовить следующие инструменты и устройства:
- рулетка или стандартная линейка;
- штангенциркуль;
- фотоаппарат — его задействуют при необходимости.
Если трубопровод доступен для проведения замеров, а торцы труб можно без проблем измерить, тогда достаточно иметь в распоряжении обычную линейку или рулетку. При этом следует учитывать, что используют такой метод, когда к точности предъявляются минимальные требования.
В этом случае выполняют измерение диаметра труб в такой последовательности:
- Подготовленные инструменты прикладывают к месту, где находится самая широкая часть торца изделия.

- Потом отсчитывают количество делений, соответствующих размеру диаметра.
Данный способ позволяет узнавать параметры трубопровода с точностью, составляющую несколько миллиметров. Иногда требуется определить и площадь трубопровода, что тоже весьма просто сделать.
Для измерения внешнего диаметра труб с небольшим сечением можно задействовать такой инструмент как штангенциркуль:
- Раздвигают его ножки и прикладывают к торцу изделия.
- Затем их нужно сдвинуть так, чтобы они оказались плотно прижатыми к наружной стороне стенок трубы.
- Ориентируясь на шкалу значений приспособления, узнают требуемый параметр.
Этот метод определения диаметра трубы дает довольно точные результаты, до десятых миллиметра.
Когда трубопровод недоступен для обмера и является частью уже функционирующей конструкции водоснабжения или газовой магистрали, поступают следующим образом: штангенциркуль прикладывают к трубе, к ее боковой поверхности.
Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.
Нередко в бытовых условиях возникает необходимость узнать, как измерять диаметр трубы, имеющей большое сечение. Существует простой вариант, как это сделать: достаточно знать длину окружности изделия и константу π, равную 3,14. Ненамного сложнее узнать объем трубы, выполнив простые расчеты.
Сначала при помощи рулетки или куска шнура обмеряют трубу в обхвате. Потом подставляют известные величины в формулу d=l:π, где:
d – определяемый диаметр;
l – длина измеренной окружности.
К примеру, обхват трубы составляет 62,8 сантиметра, тогда d = 62,8:3,14 =20 сантиметров или 200 миллиметров.
Бывают ситуации, когда проложенный трубопровод полностью недоступен. Тогда можно применить метод копирования. Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.
Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.
К примеру, это может быть коробок спичек, длина которого равна 5 сантиметрам. Потом этот участок трубопровода фотографируют. Последующие вычисления выполняют по фотографии. На снимке измеряют видимую толщину изделия в миллиметрах. Потом нужно перевести все полученные величины в реальные параметры трубы с учетом масштаба произведенной фотосъемки.
Измерение диаметров в производственных условиях
На больших строящихся объектах трубы до начала проведения монтажа в обязательном порядке подвергают входному контролю. Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Документация должна содержать определенную информацию, касающуюся труб:
- номинальные размеры;
- номер и дата ТУ;
- марка металла или вид пластика;
- номер товарной партии;
- итоги проведенных испытаний;
- химический анализ выплавки;
- тип термической обработки;
- результаты рентгеновской дефектоскопии.

Кроме этого, на поверхности всех изделий на расстоянии примерно 50 сантиметров от одного из торцов всегда наносят маркировку, содержащую:
- наименование производителя;
- номер плавки;
- номер изделия и его номинальные параметры;
- дату изготовления;
- эквивалент углерода.
Длину труб в производственных условиях определяют мерной проволокой. Также не возникает сложностей с тем, как измерить диаметр трубы рулеткой.
Для изделий первого класса допустимой величиной отклонения в одну или другую сторону от заявленной длины являются 15 миллиметров. Для второго класса –100 миллиметров.
У труб наружный диаметр сверяют, пользуясь формулой d = l:π-2Δр-0,2 мм, где кроме вышеописанных значений:
Δр – толщина материала рулетки;
0,2 миллиметра– припуск на прилегание инструмента к поверхности.
Допускается отклонение величины внешнего диаметра от заявленной производителем:
- для продукции с сечением не более 200 миллиметров–1,5 миллиметра;
- для больших труб – 0,7%.
В последнем случае для проверки трубной продукции пользуются ультразвуковыми измерительными приборами. Для определения толщины стенок задействуют штангенциркули, у которых деление на шкале соответствует 0,01 миллиметра. Минусовой допуск не должен превышать 5% номинальной толщины. При этом кривизна не может быть более 1,5 миллиметра на 1 погонный метр.
Из вышеописанной информации ясно, что несложно разобраться с тем, как определить диаметр трубы по длине окружности или при помощи несложных измерительных инструментов.
Как рассчитать окружность зная диаметр формула. Как найти и чему будет равна длина окружности
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса.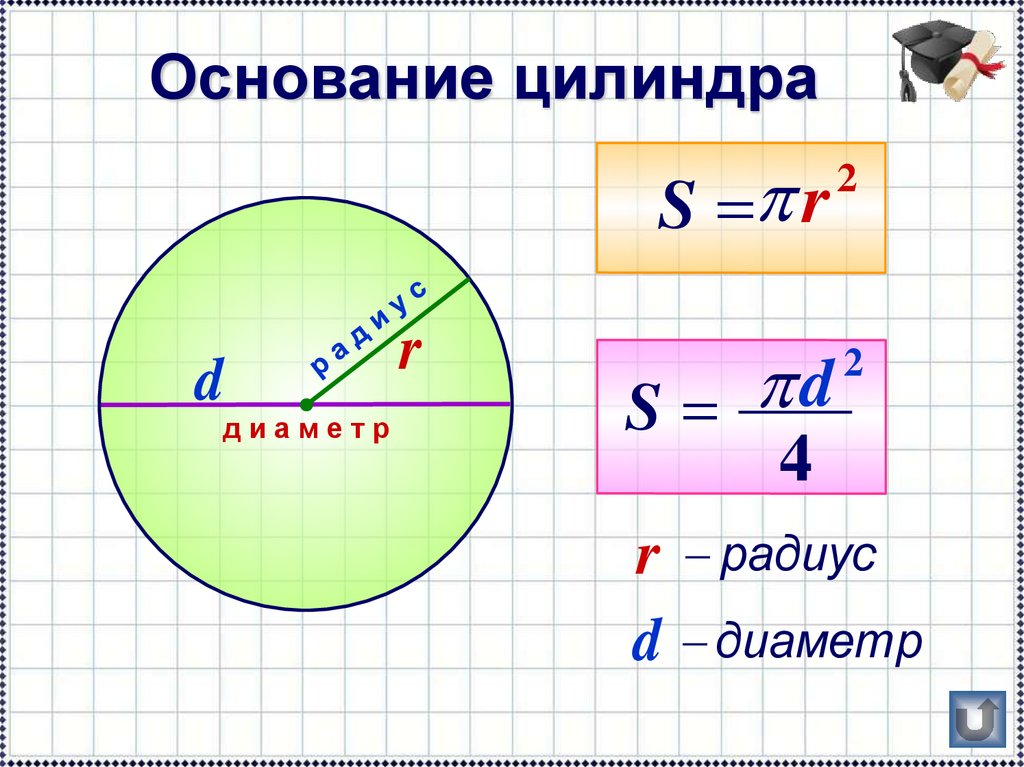 Формула нахождения площади круга :
Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
- если известен диаметр окружности, то формула выглядит так L = ПD
- если известен радиус окружности, то формула имеет следующий вид L = 2Пr.
Формула длины окружности
Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе. Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.
Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.
Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи — величина постоянная и равна 3,14.

Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.
Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.
Формула для расчета длины окружности по известной площади круга выглядит так:
L=2*корень квадратный пи*S
где S площадь круга.
Длина окружности
Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга. Она вас, при решении геометрических задач, еще не раз выручит.
Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR
На сайте quot;Сборник формулquot;, можно посчитать длину окружности, введя имеющиеся у вас данные. Там же,
Решение уравнений:
Геометрическая прогрессия:
Комбинаторика:
Решить химическое уравнение
Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом. Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Формула выглядит так:
Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.
Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности
Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.
Длину окружности с радиусом вычисляют по формуле
Длина окружности L равно 2pi умножить на R.
Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.
r — это радиус
D — диаметр
Приблизительно 3,14
Но окружность — это не круг
Смотрите картинку, на которой видна разница между кругом и окружностью
Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
Формула, таким образом, выглядит так: L=d или L=2R , где L — значение длины окружности, получаемое умножением числа (3,14) на величину радиуса окружности или двойного диаметра.
Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3. 14.
14.
Формула длины окружности равна Пи умноженное на Диаметр или Пи умноженное на Радиус умноженный на 2.
Длину окружности можно найти одним из представленных способов:
В какой бы сфере экономики человек ни трудился, вольно или невольно он пользуется математическими знаниями, накопленными за многие столетия. С устройствами и механизмами, содержащими окружности, мы сталкиваемся ежедневно. Круглую форму имеет колесо, пицца, многие овощи и фрукты в разрезе образуют круг, а также тарелки, чашки, да и многое другое. Однако, правильно рассчитывать длину окружности умеет не каждый.
С устройствами и механизмами, содержащими окружности, мы сталкиваемся ежедневно. Круглую форму имеет колесо, пицца, многие овощи и фрукты в разрезе образуют круг, а также тарелки, чашки, да и многое другое. Однако, правильно рассчитывать длину окружности умеет не каждый.
Чтобы вычислить длину окружности, необходимо вначале вспомнить, что такое окружность. Это множество всех точек плоскости, равноудаленных от данной. А круг – это геометрическое место точек плоскости, находящееся внутри окружности. Из вышесказанного следует, что периметр круга и длина окружности – это одно и то же.
Способы нахождения длины окружности
Помимо математического способа нахождения периметра круга, есть и практические.
- Взять веревку или шнур и обернуть один раз вокруг.
- Затем веревку измерить, полученное число и будет длиной окружности.
- Прокатить круглый предмет один раз и посчитать длину пути. Если предмет очень небольшой, можно несколько раз обмотать его бечевкой, затем размотать нить, измерить и поделить на число витков.

- Найти требуемую величину по формуле:
L = 2πr = πD ,
где L – искомая длина;
π – константа, приблизительно равна 3,14 r – радиус окружности, расстояние от ее центра до любой точки;
D – диаметр, он равен двум радиусам.
Применение формулы, чтобы найти длину окружности
- Пример 1. Беговая дорожка проходит вокруг окружности радиусом 47,8 метров. Найти длину данной беговой дорожки, приняв π = 3,14.
L = 2πr =2*3,14*47,8 ≈ 300(м)
Ответ: 300 метров
- Пример 2. Колесо велосипеда, обернувшись 10 раз, проехало 18,85 метра. Найти радиус колеса.
18,85: 10 =1,885 (м) – это периметр колеса.
1,885: π = 1,885: 3,1416 ≈ 0,6(м) – искомый диаметр
Ответ: диаметр колеса 0,6 метра
Удивительное число π
Несмотря на кажущуюся простоту формулы, почему-то многим трудно ее запомнить. Видимо, это происходит из-за того, что в формуле есть иррациональное число π, которое не присутствует в формулах площади других фигур, например, квадрата, треугольника или ромба.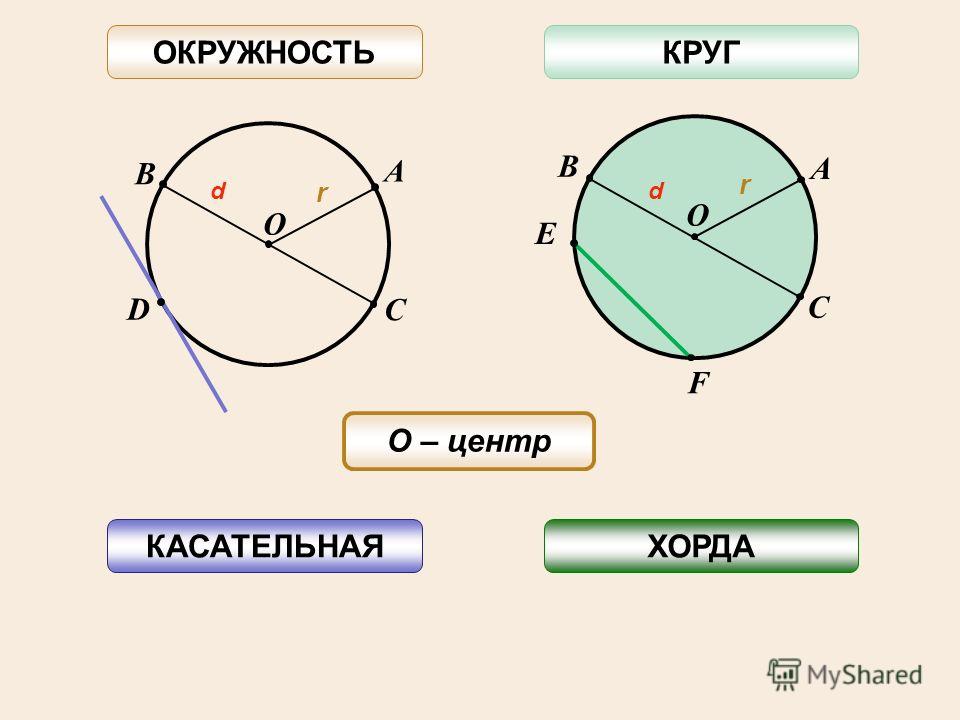 Нужно просто запомнить, что это константа, то есть постоянная, означающая отношение длины окружности к диаметру. Около 4 тысяч лет назад люди заметили, что отношение периметра круга к его радиусу (или диаметру) одинаково для любых окружностей.
Нужно просто запомнить, что это константа, то есть постоянная, означающая отношение длины окружности к диаметру. Около 4 тысяч лет назад люди заметили, что отношение периметра круга к его радиусу (или диаметру) одинаково для любых окружностей.
Древние греки приближали число π дробью 22/7. Долгое время π высчитывали как среднее между длинами вписанных и описанных многоугольников в окружность. В третьем столетии нашей эры китайский математик провёл вычисление для 3072-угольника и получил приближённое значение π = 3,1416. Необходимо помнить, что π всегда постоянно для любой окружности. Его обозначение греческой буквой π появилось в 18 веке. Это первая буква греческих слов περιφέρεια — окружность и περίμετρος — периметр. В восемнадцатом веке было доказано, что эта величина иррациональна, то есть ее нельзя представить в виде m/n, где m – целое, а n – натуральное число.
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см.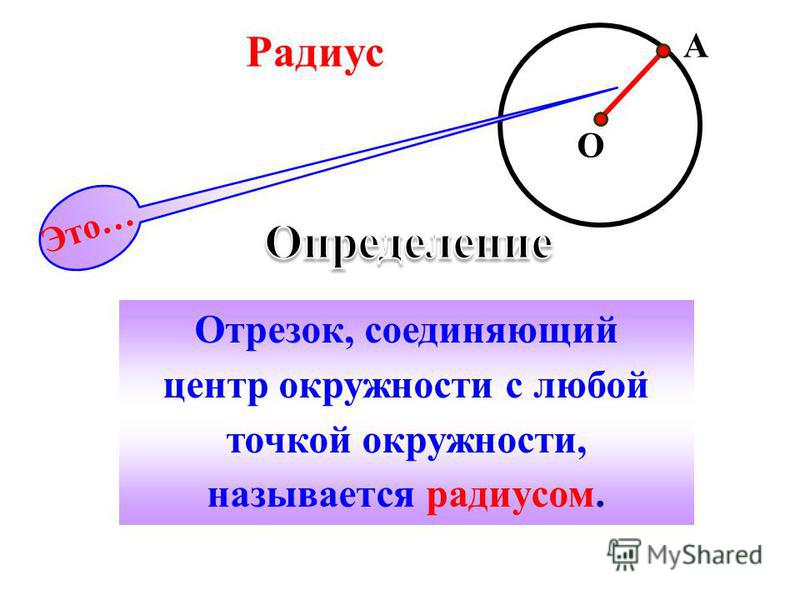 Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Как рассчитать диаметр зная длину полосы. Как вычислить диаметр окружности: формула и пояснения
Инструкция
В случае, если известен только диаметр, то формула будет выглядеть как «R = D/2».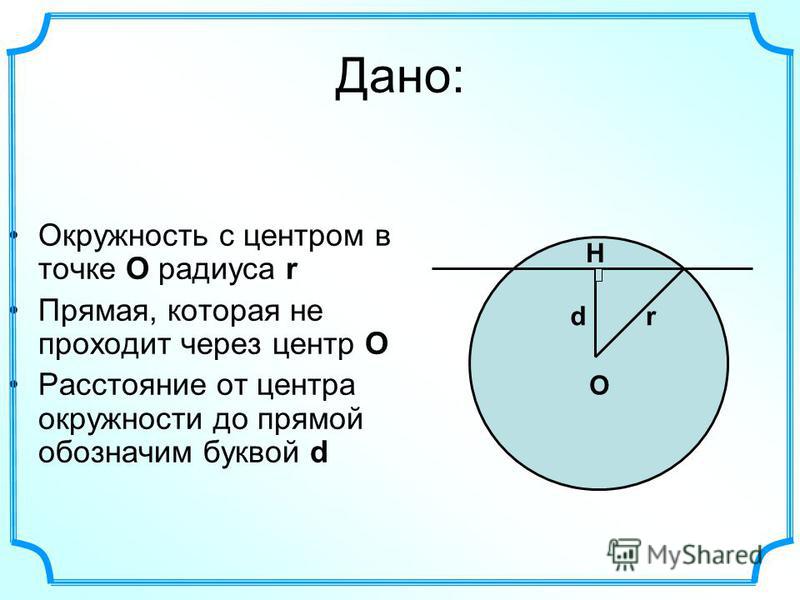 2»).
2»).
Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.
Инструкция
Если надо найти площадь (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в длину диаметра , а результат делите на четыре: S=π ²*D²/4. Например, круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 сантиметров.
Если надо найти площадь квадрата (S) по диаметру вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.
Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D². 2 / 4 + 20*10/2», а нажать клавишу Enter.
2 / 4 + 20*10/2», а нажать клавишу Enter.
Источники:
- как найти площадь окружности по диаметру
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Используйте какой-либо , чтобы рассчитать длину диаметра, если сделать это в уме не получается. Например, можно воспользоваться тем, который встроен в поисковую систему Nigma или Google — он математические операции, вводимые на «человеческом» . Например, если известная длина окружности составляет четыре метра, то для нахождения диаметра можно «по-человечески» попросить поисковик: «4 метра разделить на пи». Но если вы введете в поле поискового запроса, например, «4/пи», то поисковик поймет и такую постановку задачи. В любом случае ответом будет «1.27323954 метра».
Вопрос о диаметре земного шара не так прост, как может показаться на первый взгляд, ведь само понятие «земной шар» весьма условно. У настоящего шара диаметр всегда будет одинаковым, в каком бы месте ни был проведен отрезок, соединяющий две точки на поверхности сферы и проходящий через центр.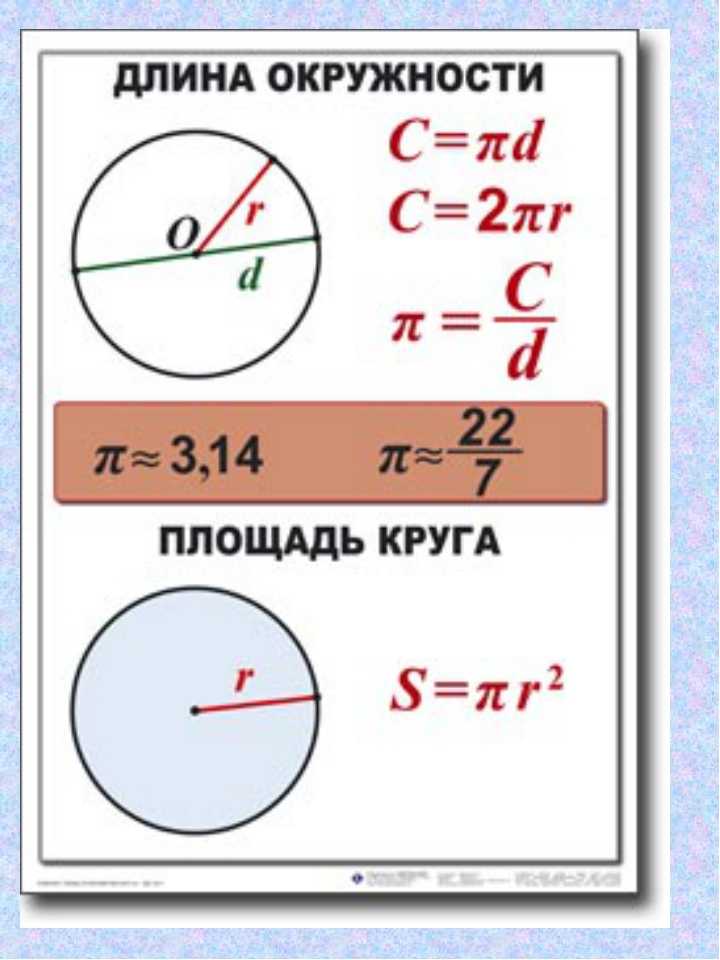
Применительно к Земле не представляется возможным, поскольку ее шарообразность далеко не идеальна (в природе вообще не бывает идеальных геометрических фигур и тел, они представляют собой абстрактные геометрические понятия). Для точного обозначения Земли ученым даже пришлось ввести специальное понятие – «геоид».
Официальный диаметр Земли
Величина диаметра Земли определяется тем, в каком месте его будут измерять. Для удобства за официально признанный диаметр принимаются два показателя: диаметр Земли по экватору и расстояние между Северным и Южным полюсами. Первый показатель равен 12 756,274 км, а второй – 12 714, разница между ними составляет немногим менее 43 км.
Данные числа не производят особого впечатления, они уступают даже расстоянию между Москвой и Краснодаром – двумя городами, расположенными на территории одной страны. Тем не менее, вычислить их было непросто.
Вычисление диаметра Земли
Диаметр планеты высчитывается по такой же геометрической формуле, как и любой другой диаметр.
Чтобы найти периметр окружности, необходимо умножить ее диаметр на число πи. Следовательно, для нахождения диаметра Земли нужно измерить ее окружность в соответствующем сечении (по экватору или в плоскости полюсов) и разделить ее на число πи.
Первым человеком, попытавшимся измерить окружность Земли, был древнегреческий ученый Эратосфен Киренский. Он обратил внимание, что в Сиене (ныне – Асуан) в день летнего солнцестояния Солнце находится в зените, освещая дно глубокого колодца. В Александрии же в этот день оно отстояло от зенита на 1/50 окружности. Из этого ученый сделал вывод, что расстояние от Александрии до Сиена составляет 1/50 окружности Земли. Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).
В распоряжении современных ученых имеются более совершенные средства измерения, но их теоретическая основа соответствует идее Эратосфена. В двух точках, расположенных в нескольких сотнях километров друг от друга, фиксируют положение Солнца или определенных звезд на небосводе и вычисляют разницу между результатами двух измерений в градусах. Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Для уточнения размеров Земли используется и лазерная дальнометрия, и спутниковые системы наблюдения.
На сегодняшний день считается, что окружность Земли по экватору составляет 40 075,017 км, а по – 40 007,86. Эратосфен лишь немного ошибся.
Величина и окружности, и диаметра Земли увеличивается из-за метеоритного вещества, постоянно выпадающего на Землю, но процесс этот идет очень медленно.
Источники:
- Как измерили Землю в 2019
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом.
 При этом отрезок АВ – диаметр.
При этом отрезок АВ – диаметр. - Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l 1 = 18,84 см, l 2 = 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
Чтобы написать, как найти диаметр круга, необходимо сначала определить, что это такое. Итак, диаметр круга — это прямая, которая проходит через центр круга и соединяет точки на окружности.
Ниже мы рассмотрим способы нахождения диаметра окружности через её длину, площадь вписанного круга, и через радиус.
Определение диаметра
Принято считать, что какой бы величины ни была окружность, отношение ее длины к диаметру — это постоянное число «Пи», которое примерно равно 3,14. Чтобы понять, как найти диаметр круга, следует привести формулы и на примере показать вычисления данной величины.
Радиус
Если известен радиус круга, то диаметр вычислить очень просто:
D = 2R, где D — это диаметр, а R — радиус. Получается, диаметр равен двум радиусам. Например, известно, что радиус равен 10 см, тогда диаметр вычисляем так: D=2*10, получается, что диаметр равен 20 см.
Получается, диаметр равен двум радиусам. Например, известно, что радиус равен 10 см, тогда диаметр вычисляем так: D=2*10, получается, что диаметр равен 20 см.
Длина окружности
В случае, если известна длина окружности, для вычисления может быть полезным число . Вот какой формулой можно воспользоваться: D = l/, где l — это длина круга. Получается, если длина окружности равна 18 см, то диаметр вычисляем так: D = 18 / 3,14 ≈ 5,73 см.
Площадь круга
Если известна только площадь круга, то это значение также можно применить. При этом площадь обозначается буквой S. Исходя из формулы S=R 2 , можно найти радиус, а значит, и диаметр. Итак, радиус R = √ (S / ). Для нахождения радиуса делим площадь на число Пи и извлекаем из этого значения квадратный корень. Таким образом, если площадь равна 25 см, то радиус вычисляется так: R = √ (25 / 3,14) ≈ √8 ≈ 2,8 см. Затем можно вычислить диаметр: D = 2R, D = 2,8*2= 5,6 см.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Диаметр круга | Определение | Пример и формула
Абдур Рохман
Содержание
Определение диаметра окружности
Диаметр окружности может быть определен как самая длинная хорда, проходящая через центр окружности. Для данного круга можно нарисовать бесконечное число диаметров .
Таким образом, для линейного сегмента Диаметр окружности , должны быть выполнены следующие два условия:
- Отрезок должен быть хордой окружности, что означает, что начальная и конечная точки отрезка должны лежать на окружности и
- Линия должна проходить через центр круга.

Отрезок линии QOR, представленный красным цветом на приведенном выше рисунке, называется Диаметром Круга. И начальная, и конечная точки линии QOR лежат на окружности, а линия проходит через центр O.
Радиус окружности — это расстояние от центра до любой точки окружности. Следовательно, диаметр в два раза больше длины радиуса. Диаметр круга можно обозначить буквой d. Следует отметить, что существует бесконечное число диаметров для данной окружности. Математически
Диаметр = 2 х радиус
\,\,\,\,d = 2 х r
Как найти диаметр окружности по окружности?
Диаметр круга можно узнать из длины окружности. Формула для нахождения окружности круга с точки зрения диаметра задается как,
C=\pi \times d
Следовательно, диаметра с точки зрения окружности будет,
d=\frac {C}{\pi}
Как найти диаметр круга из площади?
Диаметр Круга также можно узнать из Площади Круга. Формула нахождения площади круга из 92=\frac{4A}{\pi}
Формула нахождения площади круга из 92=\frac{4A}{\pi}
d=\sqrt{\frac{4A}{\pi}}
d=2\times \sqrt{\frac{A}{\pi}}
Diameter of a Circle Formulas
The different formulas for finding out the Diameter of a Circle are tabulated below:
| Serial No. | Description | Formula |
| 1 | In члены радиуса | \следовательно\,\,\,\,d = 2 \times r |
| 2 | По окружности | d=\frac{C}{\pi} |
| 3 | По площади | d=2\times \sqrt{\frac{A}{\pi }} |
Часто задаваемые вопросы (FAQ)
1. Определить диаметр окружности?
Определить диаметр окружности?
Ответ: Диаметр окружности может быть определен как самая длинная хорда, проходящая через центр окружности. Для данного круга бесконечное число Можно рисовать диаметры.
2. Как измерить диаметр круга?
Ответ: Диаметр окружности можно узнать по трем формулам:
Если известен радиус окружности: d = 2 \times r
Если известна длина окружности: d=\ frac{C}{\pi}
Если площадь круга известна: d=2\times \sqrt{{A}{\pi}}
3. Диаметр круга равен ____________?
Ответ: Диаметр окружности – это хорда, проходящая через центр окружности.
4. Как найти диаметр круга?
Ответ: Диаметр окружности можно узнать по трем формулам:
Если известен радиус окружности: d = 2 \times r
Если известна длина окружности: d=\ frac{C}{\pi}
Если площадь круга известна: d=2\times \sqrt{{A}{\pi}}
5. Что такое диаметр определения круга?
Что такое диаметр определения круга?
Ответ: Диаметр окружности может быть определен как самая длинная хорда, проходящая через центр окружности. Для данного круга можно нарисовать бесконечное количество диаметров.
Абдур Рохман
Привет, меня зовут Абдур Рохман . По профессии я инженер-электрик . Я также работаю неполный рабочий день Учитель , Блогер и Предприниматель . Причина создания этого веб-сайта или блога в основном состоит в том, что Я люблю учить . Всякий раз, когда у меня есть время, я обучаю студентов/аспирантов независимо от их класса или стандартов. Подробнее
Категории Круг Метки Диаметр кругаQ4 Диаметром окружности называется линия, соединяющая две точки на окружности, а также проходящая через т…
Перейти к
- Упражнение 11.
 1
1 - Упражнение 11.2
- Упражнение 11.3
- Упражнение 11.4
- Упражнение 11.5
- Зная наши цифры
- Целые числа
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 11 — Алгебра
>
Упражнение 11. 2
>
Вопрос 7
2
>
Вопрос 7
Вопрос 7 Упражнение 11.2
В4) Диаметром окружности называется линия, соединяющая две точки окружности и проходящая через центр окружности. (На соседнем рисунке АВ — диаметр окружности, С — ее центр). Выразите диаметр окружности (d) через ее радиус (r).
Ответ:
Решение:
Поскольку длина диаметра в два раза больше длины радиуса.
Следовательно, d = 2r
Стенограмма видео
Добро пожаловать, Келли. Нет домашнего задания. Сегодня. Мы смотрим на вопрос номер четыре: диаметр круга — это линия, соединяющая две точки на круге и также проходящая через центр. Хорошо. Теперь нам нужно выразить диаметр окружности через радиус. Прежде всего, давайте посмотрим на эту цифру, а именно на диаметр. Так что это дано здесь в 25 диаметре, за исключением диаметра сейчас, можете ли вы определить, что вы видите? Хм, так что c 2 a от центра, если вы присоединитесь к линии в любую точку, столько линий в этом году CA будет вашим радиусом.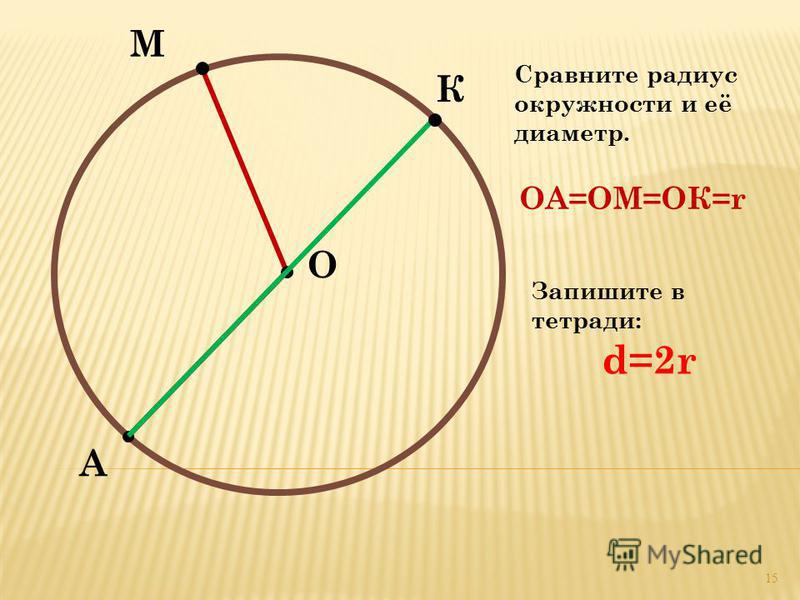 Таким образом, это ваш радиус, который дан вам как нашему генеральному директору, чтобы использовать радиусы в этой должности. Хорошо. То, что теперь видно на PC2, это тоже, потому что это одно и то же. Так что это тоже Р. Теперь. Вы должны выразить b, то есть диаметр, через радиус. Таким образом, ваш чай будет столько-то, что равно одному R плюс столько-то, то есть еще один день, когда ваше D станет 2R. Таким образом, диаметр в пересчете на радиус равен 2. Всем большое спасибо, ребята, за просмотр видео. Если у вас есть еще какие-либо сомнения, размещены в разделе комментариев. Так же поставьте лайк под видео и подпишитесь
Таким образом, это ваш радиус, который дан вам как нашему генеральному директору, чтобы использовать радиусы в этой должности. Хорошо. То, что теперь видно на PC2, это тоже, потому что это одно и то же. Так что это тоже Р. Теперь. Вы должны выразить b, то есть диаметр, через радиус. Таким образом, ваш чай будет столько-то, что равно одному R плюс столько-то, то есть еще один день, когда ваше D станет 2R. Таким образом, диаметр в пересчете на радиус равен 2. Всем большое спасибо, ребята, за просмотр видео. Если у вас есть еще какие-либо сомнения, размещены в разделе комментариев. Так же поставьте лайк под видео и подпишитесь
Связанные вопросы
Q1) Сторона равностороннего треугольника обозначена буквой l. Выразите периметр равностороннего треугольника…
Сторона равностороннего треугольника обозначена буквой l. Выразите периметр равностороннего треугольника…
Сторону правильного шестиугольника (рис. ) обозначим через l. Выразите периметр шестиугольника через l…
) обозначим через l. Выразите периметр шестиугольника через l…
Q2) Сторона правильного шестиугольника обозначается l. Выразите периметр шестиугольника через l.
Q3) Куб – это трехмерная фигура. У него шесть граней, и все они одинаковые квадраты. Т…
Куб — это трехмерная фигура, как показано на рис. 11.11. У него шесть лиц, и все они идентичны…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнение
Упражнение 11. 1
1
Упражнение 11.2
Упражнение 11.3
Упражнение 11.4
Упражнение 11.5
Главы
Knowing Our Numbers
Whole Numbers
Playing With Numbers
Basic Geometrical Ideas
Understanding Elementary Shapes
Integers
Fractions
Decimals
Data Handling
Mensuration
Algebra
Ratio and Proportion
Symmetry
Практическая геометрия
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Calize Tutorials Pvt Ltd Все права защищены
Circle Calculator
Generate Work
Отчет об этом AD
GENERGATE WORK
Область и окружно периметр и площадь круга.
Это онлайн-инструмент геометрии, для которого требуется длина радиуса круга. Используя этот калькулятор, мы разберемся, как найти периметр и площадь круга.
Необходимо выполнить следующие шаги:
- Введите в поле длину радиуса окружности. Значение должно быть положительным вещественным числом или параметром. Обратите внимание, что длина сегмента всегда положительна;
- Нажмите кнопку «СОЗДАТЬ РАБОТУ» , чтобы выполнить вычисление;
- Калькулятор окружности покажет периметр и площадь круга.
Ввод: Положительное действительное число или параметр в виде длины радиуса окружности;
Вывод : Два положительных действительных числа или переменных как периметр и площадь круга и соответствующие единицы после этого.
Формула окружности:
Длина окружности (периметр) формулы окружности: Длина окружности определяется по следующей формуле
$$C=D\раз\пи$$
где $D$ — длина диаметра окружности и $\pi\приблизительно3. 14$.
14$.
Длина окружности (периметр) круга Формула: Длина окружности определяется по следующей формуле $$C=2\раз г\раз\пи$$ где $r$ — длина радиуса окружности и $\pi\приблизительно3.14$. 92\раз\пи$$ где $r$ — длина радиуса окружности и $\pi\приблизительно3.14$.
Множество точек на плоскости, равноудаленных от данной точки $O$, представляет собой окружность. Точка $O$ называется центром окружности.
Расстояние от центра круга до любой точки на круге называется радиусом этого круга. Радиус круга должен быть положительным действительным числом. Окружность с центром $O$ и радиусом $r$ обозначается $c(O,r)$.
Расстояние по окружности называется периметром или окружностью круга. Обычно обозначается $C$.
Если все вершины многоугольника принадлежат окружности, то многоугольник называется вписанным. Если все стороны многоугольника касаются окружности, то многоугольник называется описанным.
Метод нахождения длины окружности: Впишем в окружность правильный многоугольник, например квадрат.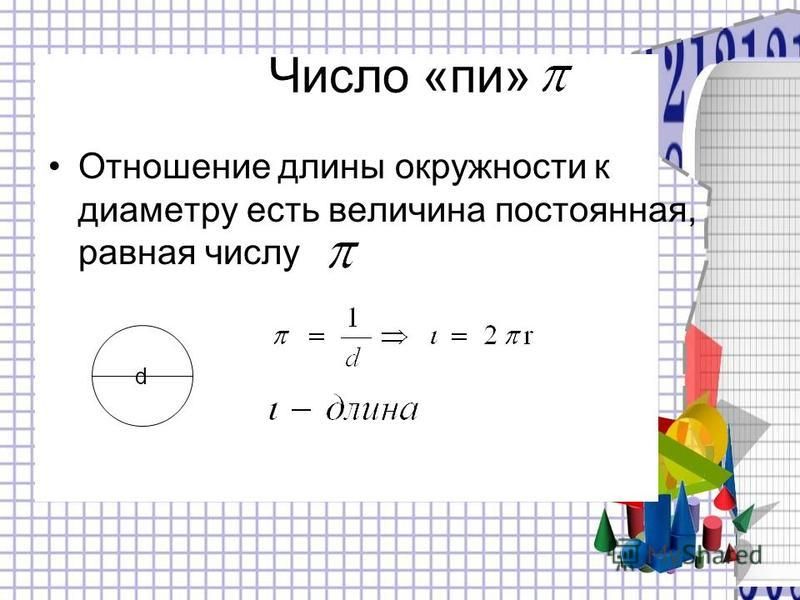 Затем удвойте количество сторон этого многоугольника, чтобы получить восьмиугольник. Если мы продолжим процесс удвоения числа сторон
правильных вписанных многоугольников, мы получаем бесконечную возрастающую последовательность периметров правильных многоугольников. Эта возрастающая последовательность ограничена, поскольку периметры всех вписанных выпуклых многоугольников меньше периметра любого описанного многоугольника.
Итак, эта возрастающая последовательность периметров имеет определенный предел. Этот предел и есть окружность. Следовательно, длина окружности есть предел периметра правильного многоугольника, вписанного в окружность, при неограниченном удвоении числа его вершин. Поскольку все круги подобны, отношение длины окружности к диаметру одинаково для всех кругов. Это отношение длины окружности к диаметру обозначается греческой буквой $\pi\приблизительно 3,14$. Таким образом, формула длины окружности равна 9.0007
Затем удвойте количество сторон этого многоугольника, чтобы получить восьмиугольник. Если мы продолжим процесс удвоения числа сторон
правильных вписанных многоугольников, мы получаем бесконечную возрастающую последовательность периметров правильных многоугольников. Эта возрастающая последовательность ограничена, поскольку периметры всех вписанных выпуклых многоугольников меньше периметра любого описанного многоугольника.
Итак, эта возрастающая последовательность периметров имеет определенный предел. Этот предел и есть окружность. Следовательно, длина окружности есть предел периметра правильного многоугольника, вписанного в окружность, при неограниченном удвоении числа его вершин. Поскольку все круги подобны, отношение длины окружности к диаметру одинаково для всех кругов. Это отношение длины окружности к диаметру обозначается греческой буквой $\pi\приблизительно 3,14$. Таким образом, формула длины окружности равна 9.0007
$$C=D\times \pi$$
или
$$C=2\times r\times \pi$$
Архимед [Heath, TL, it A History of Greek Mathematics, 2 vol.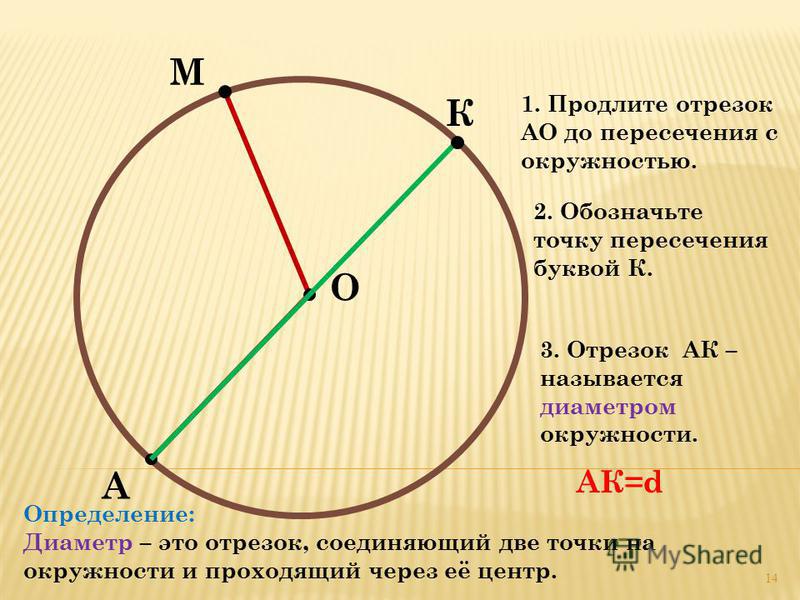 ., Oxford, 1921] дал аппроксимацию $\pi$ с помощью
$$\pi\приблизительно \frac{22}7= 3.142857142857…$$
., Oxford, 1921] дал аппроксимацию $\pi$ с помощью
$$\pi\приблизительно \frac{22}7= 3.142857142857…$$
Метод нахождения площади круга: Площадь круга – это количество квадратных единиц внутри этого круга. Разделив круг на равные
части, как показано на рисунке ниже, мы можем переставить части в примерный прямоугольник. Длина
этот приблизительный прямоугольник равен половине окружности круга, $r\times\pi$. Ширина этого приблизительного прямоугольника равна радиусу $r$ окружности.
Поскольку площадь прямоугольника равна произведению его длины на ширину, площадь этого приблизительного прямоугольника равна 92)$ и т.д.
Площадь и периметр круга с шагами показывает полный пошаговый расчет для нахождения длины окружности и площади круга с радиусом $8\;in$ с использованием длины окружности и площади формулы. За
любое другое значение длины радиуса круга, просто укажите положительное действительное число и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот круговой калькулятор для выполнения работы, проверки результатов периметра и площади двумерных фигур или эффективного выполнения домашних заданий. Они могут использовать эти методы для определения площади и длины частей круга.
Они могут использовать эти методы для определения площади и длины частей круга.
Реальные задачи с использованием площади и периметра круга
Вычисление площади и длины окружности играет важную роль почти во всех областях науки и реальной жизни. Например, формулу длины окружности и площади круга можно применить к геометрии. Они используются для изучения многих других формул и математических уравнений. Длина арки – это часть окружности круга.
Отношение длины дуги к длине окружности равно отношению длины дуги к $360$ градусам. Сектором окружности называется область, ограниченная двумя радиусами окружности и дугой, образующей их.
Площадь поверхности и объем цилиндра и конуса с круглыми основаниями содержат формулу площади круга. Боковая поверхность конуса состоит из всех отрезков, соединяющих вершину с точками на основании. Если разрезать его по наклонной высоте, то боковая поверхность будет сектором окружности. Итак, боковая площадь конуса также использует формулу площади круга.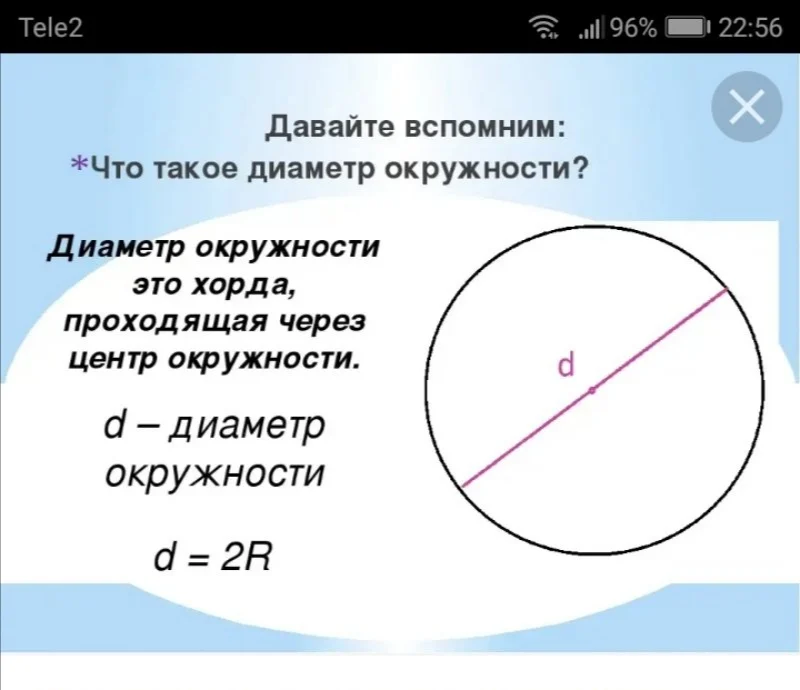
Круговые практические задачи
Практическая задача 1:
Пицца разделена на равные по 8$ куски. Диаметр пиццы составляет $25$ сантиметров. Найдите площадь одного куска пиццы.
Практическая задача 2:
Дана шина диаметром $100$ сантиметров. Сколько оборотов делает шина, проехав 10$ километров?
Калькулятор круга, формула, пример расчета (работа с шагами), задачи из реальной жизни и практические задачи будут очень полезны учащимся начальной школы (K-12 образование), чтобы понять концепцию периметра и площади круга. Это понятие может иметь значение в геометрии, для нахождения периметра, площади и объема твердых тел. Реальные задачи на окружности, связанные с длиной дуги, сектором окружности, площадью и окружностью, очень распространены, поэтому эта концепция может иметь большое значение при решении задач.
Как рассчитать периметр круга
Окружность круга
Окружность означает «периметр круга».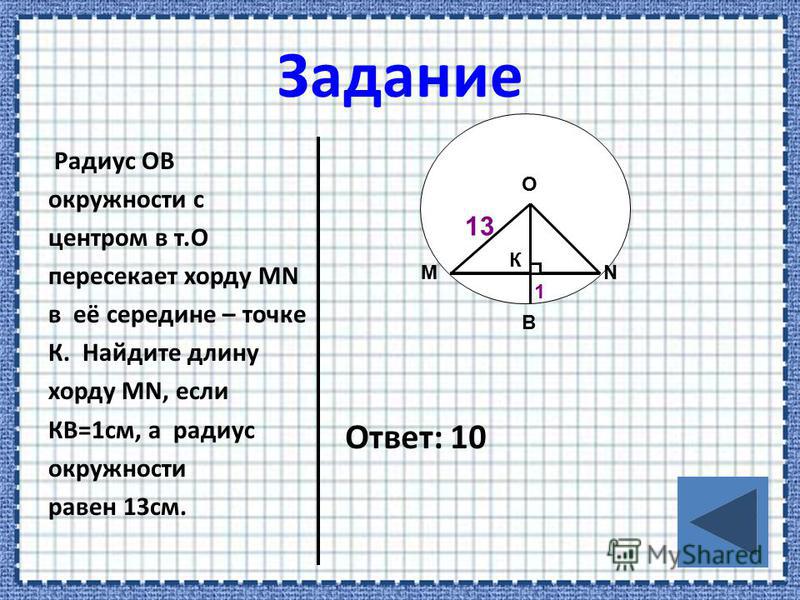 Слово произошло от латинского слова «circumferre», что означает носить с собой.
Слово произошло от латинского слова «circumferre», что означает носить с собой.
Расстояние вокруг круглой области также известно как ее окружность.
Примечание:
- Отношение длины окружности к диаметру приблизительно такое же, около 3,142.
т.е. длина окружности чуть более чем в 3 раза больше его диаметра.
Таким образом, имеем Постоянное отношение длины окружности к диаметру, т. е. 3,142 обозначается греческой буквой π, читается как пи (π). - Для расчетов значение \(\frac { 22 }{ 7 }\) принимается равным или 3,14 прибл.
∴ C = π × d ⇒ C = π × 2r
⇒ C = 2πr, где r — радиус окружности.
т. е. длина окружности = 2 × радиус окружности × π
или длина окружности = диаметр окружности × π - длина окружности полукруга = \(\frac { 2\pi r }{ 2 }\) = πr, а периметр полукруга = (π + 2) r единиц.
Пример 1: Если периметр полукруглого транспортира равен 66 см, найдите диаметр транспортира (примите π = 22/7).
Решение: Пусть радиус транспортира равен r см. Тогда
Периметр = 66 см
⇒ 1/2(2 πr) = 66 \(\left[ \text{Периметр}\text{of}\text{полукруг}\text{=}\frac{\text {1}}{\text{2}}\text{(2 }\!\!\pi\!\!\text{ r)} \right]\)
⇒ πr = 66
⇒ \(\frac { 22 }{ 7 }\) × r = 66
⇒ r = 21 см
∴ Диаметр транспортира = 2r = (2 × 21) см
= 42 см
Подробнее:
- Части окружности
- Общая хорда двух пересекающихся окружностей
- Построение окружности
- Площадь окружности
- Свойства окружностей
- Сектор окружности
- Площадь отрезка окружности 9002 9002 A8 Площадь сектора круга
Пример 2: Длина окружности больше диаметра на 16,8 см. Найдите радиус окружности.
Найдите радиус окружности.
Решение: Пусть радиус окружности равен r см. Тогда
Диаметр = 2r см и Окружность = 2πr см
Дано, что длина окружности больше диаметра на 16,8 см
∴ Окружность = Диаметр + 16,8
⇒ 2πr = 2r + 16,8
⇒ 2 × \(\frac { 22 } { 7 }\) × r = 2r + 16,8
⇒ 44r = 14r + 16,8 × 7
⇒ 44r – 14r = 117,6 ⇒ 30 r = 117,6
⇒ r = \(\frac { 117,6 }{ 30 }\) = 3,92
Следовательно, радиус = 3,92 см. Он повторно сгибается в квадратную форму. Определить длину стороны квадрата.
Решение: У нас есть,
Длина провода = длина окружности
Длина провода = 2 × \(\frac { 22 }{ 7 }\) × 28 см [Используя C = 2πr]
Длина провод = 176 см ….(i)
Пусть сторона квадрата равна x см. Затем
Периметр квадрата = Длина провода
⇒ 4x = 176 [Используя (i)]
⇒ x = 44 см
Следовательно, длина сторон квадрата равна 44 см.
Пример 4: Гоночная трасса имеет форму кольца, внутренняя окружность которого составляет 352 м, а внешняя – 396 м.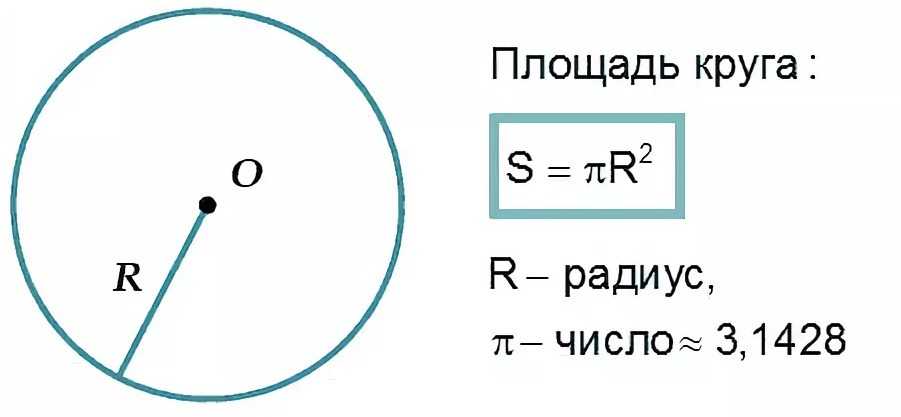 Найдите ширину дорожки.
Найдите ширину дорожки.
Решение: Пусть внешний и внутренний радиусы кольца равны R метров и r метров соответственно. Тогда
2πR = 396 и 2πr = 352
⇒ 2 × \(\frac { 22}{7}\) × R = 396 и 2 × \(\frac {22}{7}\) × r = 352
⇒ R = 396 × \(\frac {7}{22}\) × \(\frac {1}{2}\ ) и r = 352 × \(\frac { 7 }{ 22 }\) × \(\frac { 1 }{ 2 }\)
⇒ R = 63 м и r = 56 м
Следовательно, ширина пути = (R – r) метров
= (63 – 56) метров = 7 метров
Пример 5: Внутренняя окружность кольцевой дорожки составляет 220 м. Ширина трассы везде 7 метров. Рассчитайте стоимость возведения забора по внешнему кругу из расчета j – 2 за метр. (Используйте π = 22/7)
Решение: Пусть внутренний и внешний радиусы круговой дорожки равны r метрам и R метрам соответственно. Тогда
Внутренняя окружность = 220 метров
⇒ 2πr = 220 ⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 220 ⇒ r = 35 м
Так как дорожка везде имеет ширину 7 метров.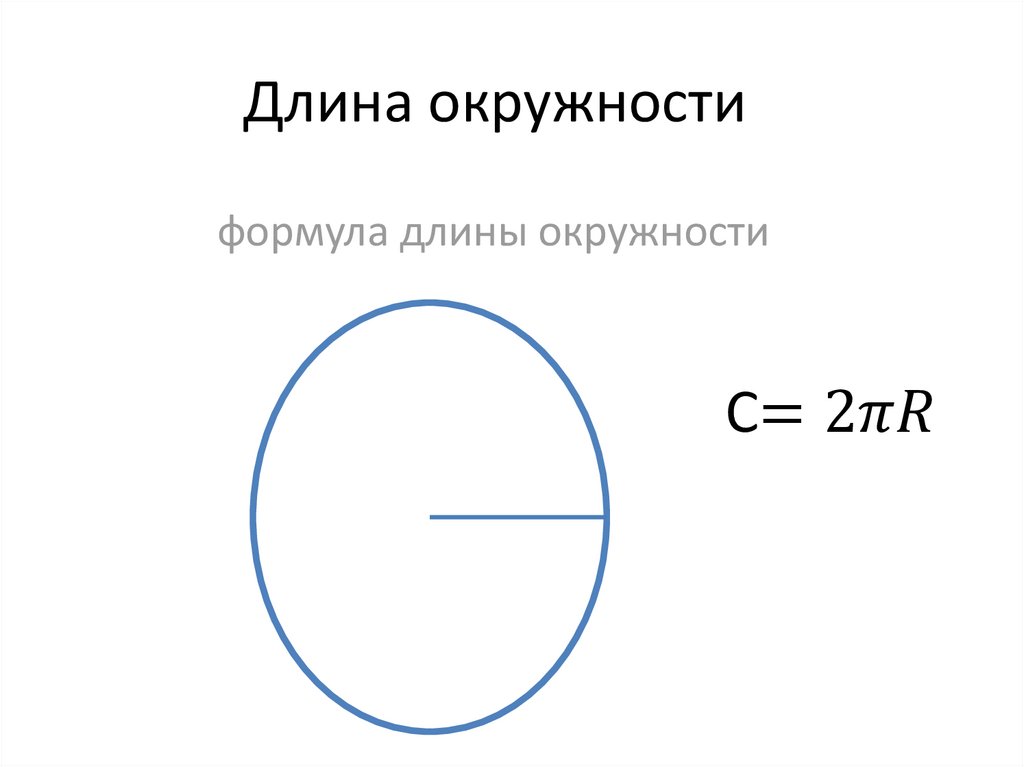 Следовательно,
Следовательно,
R = Внешний радиус = r + 7 = (35 + 7) m = 42 м
∴ Наружная окружность
= 2πR = 2 × \(\frac { 22 }{ 7 }\) × 42 м = 264 м
Ставка ограждения = j – 2 на метр
∴ Общая стоимость ограждения
= (Окружность × Скорость) = j – (264 × 2) = j – 528
Пример 6: Велосипедное колесо совершает 5000 оборотов, проезжая 11 км. Найдите диаметр колеса.
Решение: Пусть радиус колеса равен r см.
Расстояние, проходимое колесом за один оборот \(=\frac{\text{Расстояние}\,\,\text{перемещено}}{\text{Число}\,\,\text{of}\,\,\ text{оборот}}\text{ = }\frac{\text{11}}{\text{5000}}\text{км}\)
= \(\frac {11}{5000}\) × 1000 × 100 см = 220 см
∴ Окружность колеса = 220 см
⇒ 2πr = 220 см ⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 220
⇒ r = 35 см
∴ Диаметр = 2r см = (2× 35) см = 70 см
Значит, диаметр колеса 70 см.
Пример 7: Автомобиль имеет колеса диаметром 80 см. Сколько полных оборотов делает каждое колесо за 10 мин, если автомобиль движется со скоростью 66 км/ч?
Решение: Имеем,
Скорость автомобиля = 66 км/ч
∴ Расстояние, пройденное автомобилем за 1 час = 66 км
⇒ Расстояние, пройденное автомобилем за 10 мин.
= \(\frac { 66}{ 60 }\) × 10 км = 11 км = 11 × 1000 × 100 см
Имеем,
Радиус колес автомобиля = 40 см
∴ Окружность колес
= 2 × \ (\frac { 22 }{ 7 }\) × 40 см
⇒ Расстояние, пройденное автомобилем за один полный оборот
= 2 × \(\frac { 22 }{ 7 }\) × 40 см
∴ Число оборотов, сделанных колесами за 10 минут
\( =\frac{\text{Расстояние}\,\,\text{пройдено}\,\,\text{by}\,\,\text{the}\, \,\text{автомобиль}\,\,\text{in}\,\,\text{10}\,\,\text{минуты}}{\ \ \text{Расстояние}\,\,\,\ текст {покрыт}\,\,\текст{по}\,\,\текст{на}\,\,\текст{автомобиль}\ \текст{когда}\ \текст{его}\,\,\текст{ колеса}\ \text{сделать}\,\,\text{один}\,\,\text{полный}\,\,\text{революция}} \)
\( =\frac{11\times 100\times 100}{2\times \frac{22}{7}\times 40}=\frac{11\times 1000\times 100\times 7}{2\times 22\х40}=4375\)
Следовательно, каждое колесо делает 4375 оборотов за 10 минут.
Пример 8: Круглая клумба диаметром 1,5 м. Вокруг него должна быть установлена металлическая окантовка. Найдите необходимую длину канта и стоимость канта, если он продается метражом и стоит 60 м. (Вы можете купить только целое количество метров)
Найдите необходимую длину канта и стоимость канта, если он продается метражом и стоит 60 м. (Вы можете купить только целое количество метров)
Решение:
Сначала найдите длину окружности, сколько метров вам нужно.
∴ C = p × d = 3,14 × 1,5 = 4,71 м.
Так как необходимая длина 4,71 м, то нам необходимо купить 5 м канта.
Итак, стоимость покупки 5 м = 5 × 60 = 300.
Пример 9: Имеется круглый пруд, вдоль которого проходит пешеходная дорожка. Человек обходит его ровно один раз, держась близко к краю. Если его шаг равен 66 см и он делает ровно 400 шагов, чтобы обойти пруд. Каков диаметр пруда?
Решение:
Мы знаем, что периметр круга = πd
Длина одного шага человека = 66 см
Длина 400 шагов человека = 400 × 66 см = 26400 см
Это означает, что окружность пруда равна 26400 см
Пример 10: Круглая скатерть имеет окружность 220 см.
(a) Достаточно ли велика скатерть, чтобы поместиться на круглом столе диаметром 50 см?
(b) Если да, то какой длины скатерть будет свисать с каждой стороны?
Решение:
(а) Диаметр стола 50 см.
Следовательно, окружность стола
= π × d = π × 50 см ……(i)
и окружность ткани = 220 см
∴ Окружность ткани = 220 см
= 2 × π × 35 или 70π …. .(ii)
Как видно из (i) и (ii), мы имеем
. Скатерть достаточно велика, чтобы поместиться на круглом столе.
(b)
∴ Длина подвеса = 35 см – 25 см = 10 см
Очевидно, радиус ткани намного больше радиуса стола.
Таким образом, ткань будет свисать по 10 см с каждой стороны.
Пример 11: Хлопковая нить намотана на катушку радиусом 35 см.
(а) Какова длина хлопка на одном обороте барабана?
(b) Сколько оборотов катушки необходимо, чтобы намотать на катушку 44 м хлопка?
Решение:
(a) Ясно, что для вычисления длины витков хлопка на одном обороте барабана мы должны вычислить длину окружности барабана.
Теперь длина окружности барабана = 2πr, где r — радиус барабана.
= 2 × \(\frac { 22 }{ 7 }\) × 35 см = 220 см
Таким образом, 220 см – это необходимая длина хлопкового раунда на один оборот барабана.
(b) Так как мы знаем, что 1 м = 100 см
∴ 44 м = 4400 см
∴ 220 см — необходимая длина для совершения одного оборота.
Теперь количество витков, необходимое для завершения 1 см длины = \(\frac { 1 }{ 220 }\) витков
Итак, необходимое количество витков для завершения длины 4400 см
= 4400 × \(\frac { 1 }{ 220 }\) витков = 20 витков.
Разница между кругом и сферой: параметры и формулы
Круг и сфера и некоторые из самых популярных и изученных фигур в аналитической геометрии. И круги, и сферы круглые, но круги — это двухмерные фигуры, которые могут быть представлены на любой плоскости, тогда как сферы — это трехмерные объекты. Еще одним отличием сферы от круга является объем. Мы не можем найти объем, а только поверхность круга, но мы можем найти объем сферы.
В этой математической статье мы узнаем о разнице между кругом и сферой и сравним их на основе различных параметров, формул и многого другого.
Круг и сфера
Круг представляет собой двумерную замкнутую изогнутую фигуру. Он определяется как совокупность точек, находящихся на фиксированном расстоянии от данной точки, называемой ее центром. Некоторыми отличительными характеристиками круга являются его диаметр, радиус, окружность, касательная, хорда и многое другое. Когда нам нужно измерить окружность, мы просто находим длину ее радиуса. Радиус по определению — это линия, соединяющая центр круга с любой точкой его окружности.
На приведенном выше рисунке C представляет собой окружность с центром O, радиусом R и диаметром D. Некоторыми из распространенных примеров окружностей являются круглые ходовые часы, диски и т. д.
Сфера, в отличие от окружности, представляет собой замкнутую объемная фигура. Его можно определить как геометрическое место всех точек в трех измерениях, находящихся на равном расстоянии от фиксированной точки, называемой центром сферы.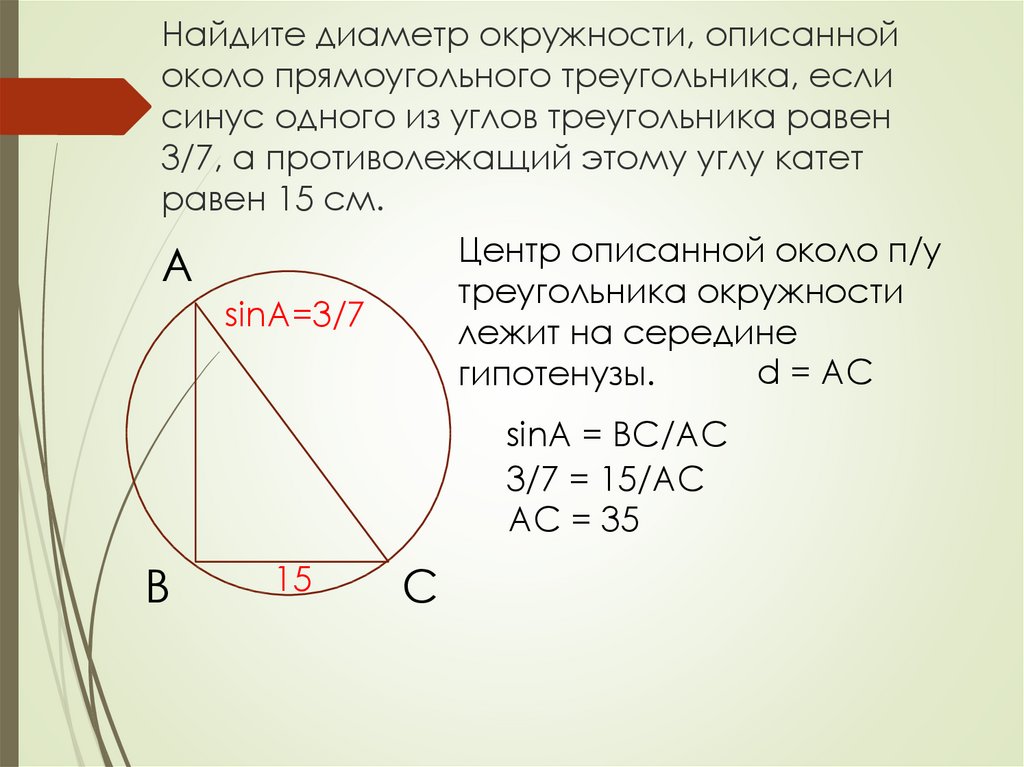 Мы также можем определить его как фигуру, образованную вращением круга вокруг его диаметра.
Мы также можем определить его как фигуру, образованную вращением круга вокруг его диаметра.
Некоторыми характерными параметрами сферы являются ее диаметр, объем, площадь поверхности и т. д. Здесь диаметр сферы — это линия, соединяющая любые две точки на поверхности сферы и проходящая через центр сферы .
Данная фигура представляет собой сферу радиусом r. Некоторыми из распространенных примеров сфер являются теннисные мячи, апельсины, глазные яблоки и т. д.
Разница между кругом и сферой
Когда мы смотрим на определение круга и сферы, обе геометрические фигуры демонстрируют точную симметрию в центр. Кроме того, все точки на краю круга или на границе сферы устанавливаются на фиксированном расстоянии от фиксированной центральной точки.
Однако между этими двумя цифрами есть определенные различия. Когда круг является двухмерной фигурой, сфера подпадает под изучение трехмерных геометрических фигур.
Давайте проверяем другую точку разницы между кружкой и сферой:
| СВОБОДА | Circle | SPEHERE |
13707077077013. линия, все точки которой находятся на фиксированном расстоянии от фиксированной точки. линия, все точки которой находятся на фиксированном расстоянии от фиксированной точки. | Это круглый космический объект, все точки которого находятся на равном расстоянии от его центра в трехмерном пространстве. | |
| Размеры | 2-мерные | 3-мерные |
| Определение | Мы можем найти площадь сферы 90,5 и площадь сферы 9070. | |
| Диаметр | Диаметр круга составляет = 2R | Диаметр сферы = 2R |
| Округа | 5.2\), здесь (a,b,c) — центр сферы, r — радиус.||
| Consideration | It is a figure | It is an object |
| Examples | Wall clock, coins | Oranges, football |
Circle of a Sphere
A круг сферы — это в основном круг, который лежит на поверхности сферы. 2\) 92\)
2\) 92\)
=\(\frac{4}{3}\pi\times196\)
=\(\frac{784}{3}\pi\)
=\(\frac{784}{ 3}\times\frac{22}{7}\)
=\(\frac{112\times22}{3}\)
=\(\frac{2464}{3}\)
=821,33 куб. Cm
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Разница между кругом и сферой. Часто задаваемые вопросы
В.1 Почему круг не является сферой?
Ответ 1 Круг — это двумерная фигура, которую можно изобразить на листе бумаги, тогда как сфера — это объект, который можно ощупать и подержать в руке.
Q.2 Какова формула сферы?
Ответ 2 Некоторые из общих формул, используемых для сфер: Если радиус сферы равен r, 92\), здесь (a,b) — центр окружности, r — радиус.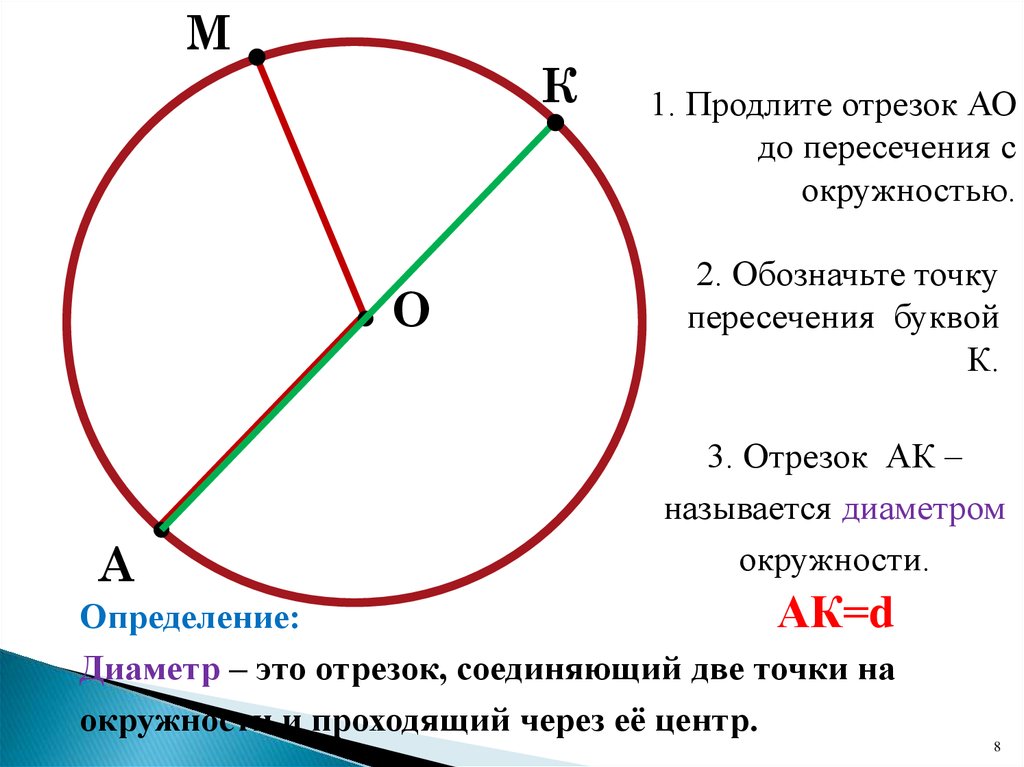

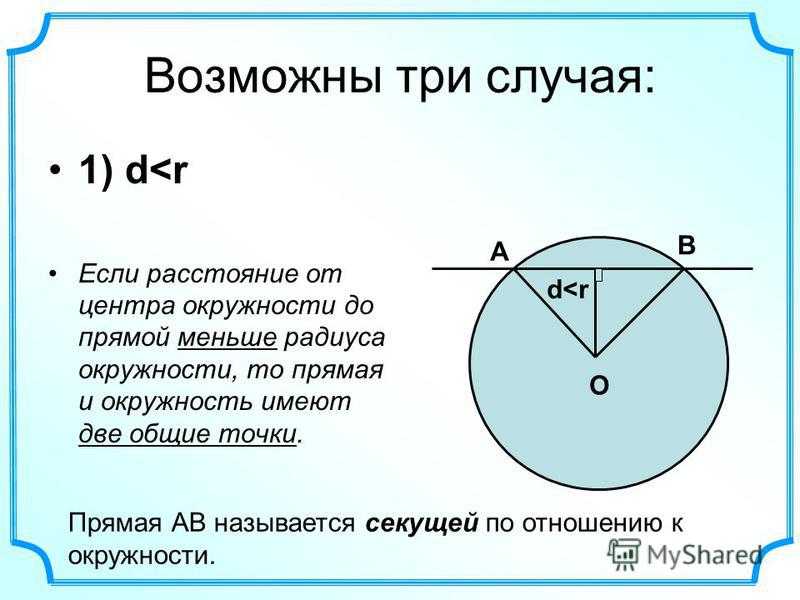

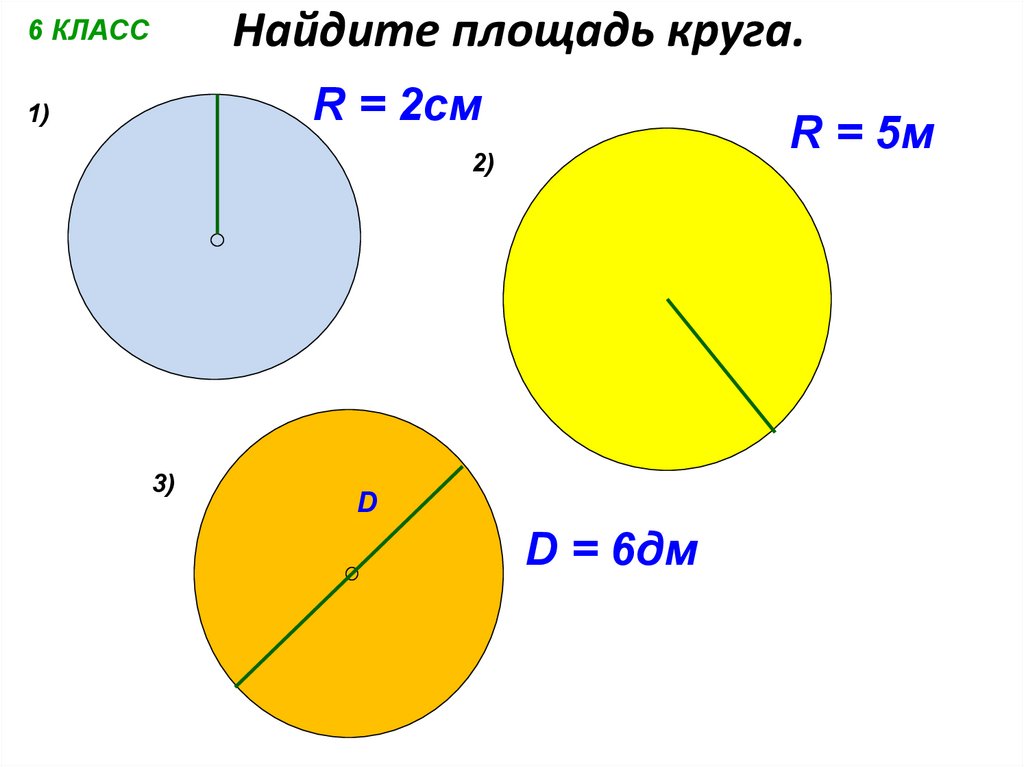
 Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.
Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.



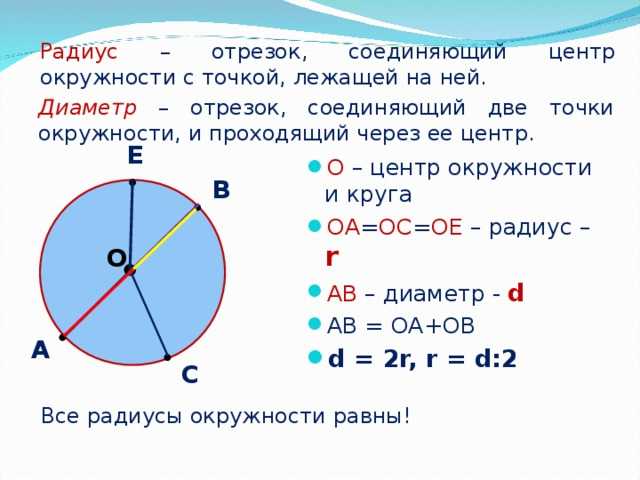 При этом отрезок АВ – диаметр.
При этом отрезок АВ – диаметр.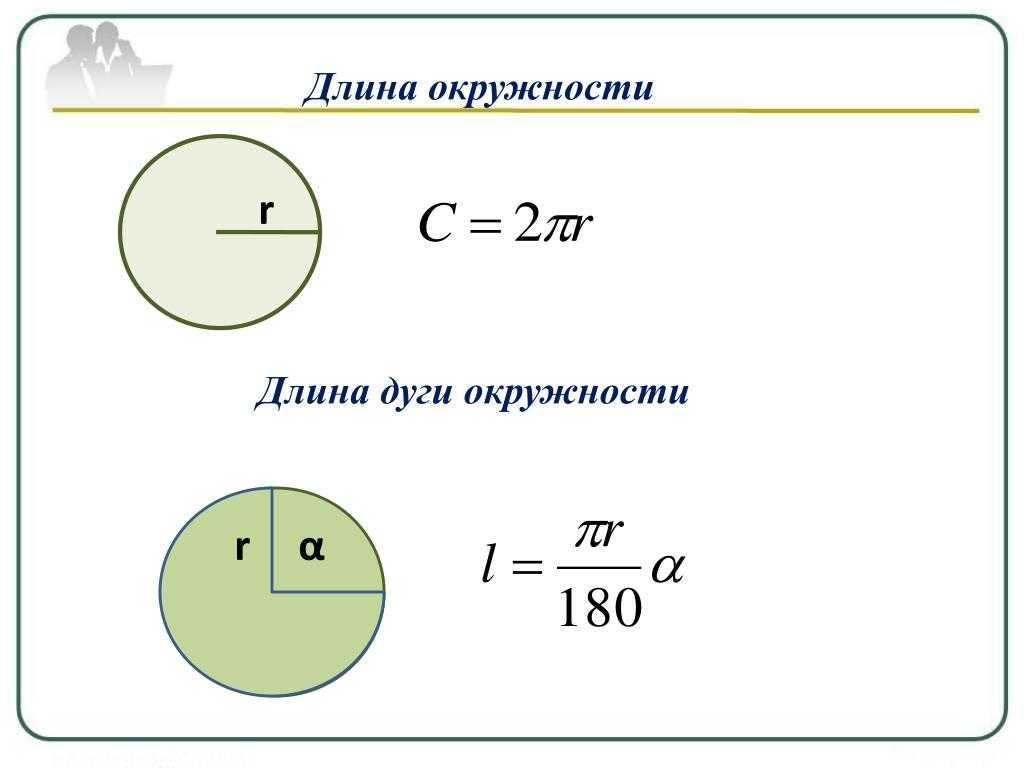
 1
1