Найти длину вектора формула: Как найти длину вектора: формула, примеры решений

примеры и решения, формулы и теоремы

Длина вектора — основные формулы

Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.

От начала координат отложим вектор OA→=a→. Определим соответственные проекции точки A на координатные оси как Ax и Ay . Теперь рассмотрим прямоугольник OAxAAy с диагональю OA.

Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.

Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.

Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.

Пример 1

Вычислить длину вектора a→=7;e, заданного в прямоугольной системе координат.

Решение

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатамa→=ax2+ay2: a→=72+e2=49+e

Ответ: a→=49+e.

Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае OA2=OAx2+OAy2+OAz2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда OA=OAx2+OAy2+OAz2. Из определения координат вектора можем записать следующие равенства OAx=ax; OAy=ay; OAz=az; , а длина ОА равна длине вектора, которую мы ищем, следовательно, OA→=OAx2+OAy2+OAz2.

Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.

Пример 2

Вычислить длину вектора a→=4·i→-3·j→+5·k→, где i→,j→,k→ — орты прямоугольной системы координат.

Решение

Дано разложение вектора a→=4·i→-3·j→+5·k→, его координаты равны a→=4,-3,5. Используя выше выведенную формулу получим a→=ax2+ay2+az2=42+(-3)2+52=52.

Ответ:a→=52.

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2

А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле

AB→=(bx-ax)2+(by-ay)2+(bz-az)2

Пример 3

Найти длину вектора AB→, если в прямоугольной системе координат A1, 3, B-3, 1.

Решение

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим AB→=(bx-ax)2+(by-ay)2: AB→=(-3-1)2+(1-3)2=20-23.

Второй вариант решения подразумевает под собой применение данных формул по очереди: AB→=(-3-1; 1-3)=(-4; 1-3); AB→=(-4)2+(1-3)2=20-23.-

Ответ: AB→=20-23.

Пример 4

Определить, при каких значениях  длина вектора AB→ равна 30, еслиA(0, 1, 2); B(5, 2, λ2) .

Решение

Для начала распишем длину вектора AB→ по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2=(5-0)2+(2-1)2+(λ2-2)2=26+(λ2-2)2

Затем полученное выражение приравняем к 30, отсюда найдем искомые λ:

 26+(λ2-2)2=3026+(λ2-2)2=30(λ2-2)2=4λ2-2=2 или λ2-2=-2  λ1=-2, λ2=2, λ3=0.

Ответ: λ1=-2, λ2=2, λ3=0.

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Пример 5

Длины векторов AB→ и AC→ равны 3 и 7 соответственно, а угол между ними равен π3. Вычислить длину вектора BC→.

Решение

Длина вектора BC→ в данном случае равна длине стороны BC треугольника △ABC. Длины сторон AB и AC треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов:BC2=AB2+AC2-2·AB·AC·cos∠(AB,→AC→)=32+72-2·3·7·cosπ3=37 ⇒BC=37 Таким образом, BC→=37.

Ответ:BC→=37.

Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Модуль вектора. Длина вектора.

Навигация по странице:

• Определение длины вектора
• Формулы для вычисления длины вектора
  • для плоских задач
  • для пространственных задач
  • для n -мерного вектора
• Примеры задач на вычисления длины вектора
  • плоские задачи
  • пространственные задачи
  • задачи в n -мерном пространстве

Смотрите также онлайн калькулятор для вычисления длины вектора.

Упражнения. Модуль вектора на плоскости.

Упражнения. Модуль вектора в пространстве.

Определение длины вектора

Определение.

Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.

Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.

Формулы длины вектора

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой:

|a| = √a_x² + a_y²

Формула длины вектора для пространственных задач

В случае пространственной задачи модуль вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой:

|a| = √a_x² + a_y² + a_z²

Формула длины n -мерного вектора

В случае n-мерного пространства модуль вектора a = {a₁ ; a₂; .

.. ; a_n} можно найти воспользовавшись следующей формулой:

|a| = (	n	ai2)1/2
	Σ
	i=1

Примеры задач на вычисление длины вектора

Примеры вычисления длины вектора для плоских задачи

Пример 1. Найти длину вектора a = {2; 4}.

Решение: |a| = √2² + 4² = √4 + 16 = √20 = 2√5.

Пример 2. Найти длину вектора a = {3; -4}.

Решение: |a| = √3² + (-4)² = √9 + 16 = √25 = 5.

Примеры вычисления длины вектора для пространственных задачи

Пример 3. Найти длину вектора a = {2; 4; 4}.

Решение: |a| = √2² + 4² + 4² = √4 + 16 + 16 = √36 = 6.

Пример 4. Найти длину вектора a = {-1; 0; -3}.

Решение: |a| = √(-1)² + 0² + (-3)² = √1 + 0 + 9 = √10.

Примеры вычисления длины вектора для пространств с размерностью большей 3

Пример 5. Найти длину вектора a = {1; -3; 3; -1}.

Решение: |a| = √1² + (-3)² + 3² + (-1)² = √1 + 9 + 9 + 1 = √20 = 2√5

Пример 6. Найти длину вектора a = {2; 4; 4; 6 ; 2}.

Решение: |a| = √2² + 4² + 4² + 6² + 2² = √4 + 16 + 16 + 36 + 4 = √76 = 2√19.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Найдите длину вектора A+B, зная длину вектора A, длину вектора B и угол между ними

Исчисление

Джон Г.

спросил 12.02.20

Предположим, что длина вектора A, [[A]] = 4, длина вектора B, [[B]] =√3, угол между ними равен Pi/6. Найдите длину A+B, [[A+B]]

Подписаться І 1

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Йосеф Т. ответил 12.02.20

Репетитор

4.9 (67)

РПИ к.т.н. Репетитор по математике/физике со страстью к преподаванию

Смотрите таких репетиторов

Посмотреть таких репетиторов

Есть два способа решить эту проблему. Один разлагает векторы на их горизонтальные и вертикальные компоненты, а затем использует теорему Пифагора, чтобы найти длину суммы. Другой использует закон косинусов. Я представлю здесь оба метода.

Разложение векторов на компоненты:

Задача никогда не говорила, в каких направлениях обращены векторы, только то, что они были разделены углом 30 градусов. (На самом деле в задаче указано число пи/6 радиан, но мы знаем, что число пи/6 радиан составляет 30 градусов.) Хорошая новость заключается в том, что мы можем принять любое направление для первого вектора и всегда получать один и тот же ответ.

Я предполагаю, что первый вектор совершенно горизонтален, а второй вектор указывает на 30 градусов вверх от горизонтали.

Мы хотим найти горизонтальную и вертикальную составляющие каждого из двух векторов, затем сложить эти компоненты, чтобы получить горизонтальную и вертикальную составляющие суммы (называемой результирующей ), и, наконец, вычислить ее длину, используя пифагорову формулу. теорема.

Первый вектор прост, потому что он горизонтальный. В задаче сказано, что длина равна 4. Получаем 9.0003

A _{горизонтальный} = 4.

A _{вертикальный} = 0.

Затем мы делаем то же самое для вектора B. Поскольку он направлен по диагонали, мы должны используйте тригонометрию, чтобы найти его горизонтальную и вертикальную составляющие. Поскольку он имеет длину √(3) и направлен под углом 30 градусов, мы получаем следующие уравнения:

B _{по горизонтали} = √3 cos (30) = 1,5 .

B _{вертикально} = √3 sin (30) = √3/2 .

Теперь складываем векторы, чтобы получить компоненты равнодействующей:

(A+B) _{горизонталь} = A _{горизонталь 9 0058 + B Горизонтальный = 4 + 1,5 = 5,5}

(А+В) _{по вертикали} = A _{по вертикали} + B _{по вертикали} = 0 + √ 3/2 = √3/2.

Наконец, мы используем теорему Пифагора, чтобы найти общую длину результирующего вектора A+B.

||А+В|| = √( ( (A+B) _{по горизонтали} ) ² + 9 0037 ( (А+Б) _{вертикально} ) ² ) = √ (5,5 ^{9003 7 2} + ( √3 /2) ² ) = √( 31)

Закон косинусов:

На первый взгляд, вы можете подумать: «Зачем здесь может быть полезен закон косинусов. Закон косинусов используется для треугольников. Это не треугольник, это сумма двух векторов». Вспомним, как сложить два вектора. Если вы рисуете один вектор, затем другой вектор, который начинается там, где заканчивается первый, то сумма или результирующий из двух векторов — это вектор, который начинается в начале первого и движется по прямой линии, заканчиваясь в конце второго вектора. Эти три вектора (A, B и результирующий) образуют треугольник.

Обратите внимание, что у нас есть длины двух векторов и угол между ними. Есть еще одна деталь, которую легко испортить. Два вектора встречаются под углом пи/6 радиан (или 30 градусов), когда они начинаются в одной и той же точке . Если вместо этого вектор B переместить в начало, где заканчивается вектор A, они фактически образуют угол 150 градусов. (Нарисовал бы картинку для демонстрации, но формат не позволяет. Может позже добавлю видео.)

Теперь, когда у нас есть длины двух векторов и угол между ними, мы можем использовать закон косинусов:

||A+B|| ² = ||А|| ² + ||В|| ² — 2||А|| ||Б|| cos(150)

||А+В|| ² = 4 ² + √3 ² 9003 7 — 2 х 4 х √3 х -√3 / 2

||А+В|| ² = 16 + 3 — (-12)

||A+B|| ² = 31

||A+B|| = √31

Голосовать за 1 голос против

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

13.3 Длина дуги и кривизна

Иногда полезно вычислить длину кривой в пространстве; для Например, если кривая представляет путь движущегося объекта, длина кривой между двумя точками может быть расстоянием, пройденным объект между двумя временами.

Напомним, что если кривая задана вектор-функцией $\bf r$, то вектор $\Delta {\bf r}= {\bf r}(t+\Delta t)-{\bf r}(t)$ точек из одной позиции на кривой к другой, как показано на рисунке 13.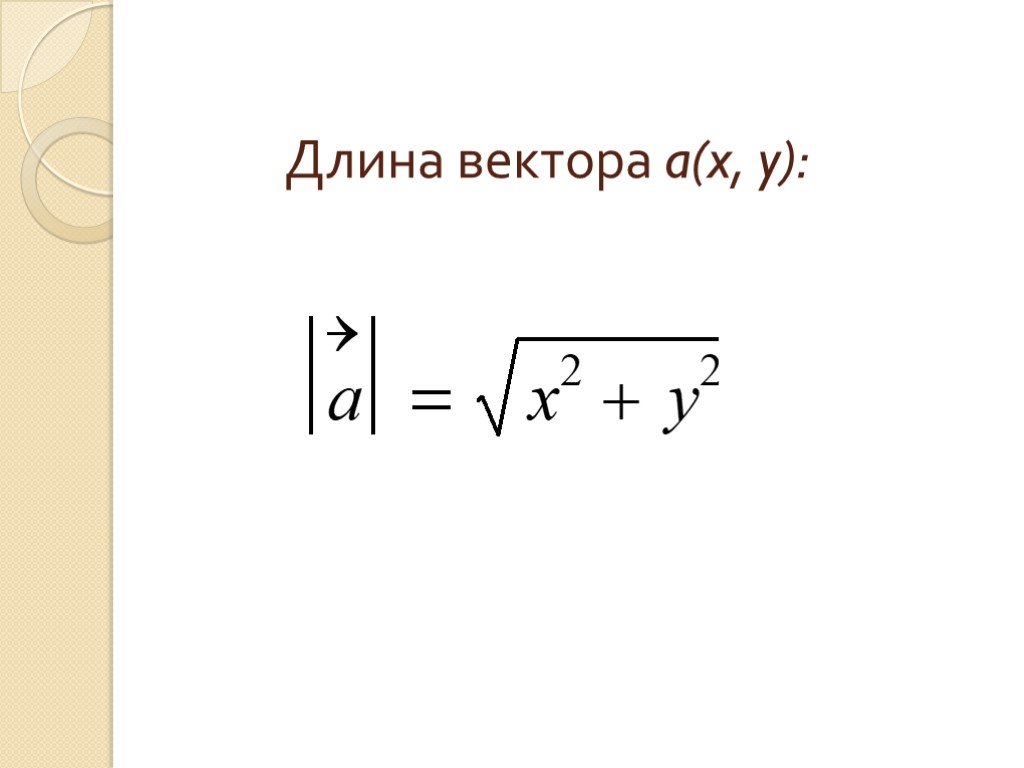 b|{\bf r}'(t)|\,dt.$$ (Ну, иногда. Это работает, если между $a$ и $b$ отрезок кривой трассируется ровно один раз.) 92}\,дх.$$ К сожалению, такие интегралы часто невозможно вычислить точно и должны быть приближены.

Одним из полезных применений длины дуги является параметризация длины дуги . Вектор функция ${\bf r}(t)$ задает положение точки с точки зрения параметр $t$, который часто является временем, но не обязательно. Предположим, что $s$ расстояние вдоль кривой от некоторой фиксированной начальной точки; если мы используем $s$ для переменной, мы получаем ${\bf r}(s)$, позицию в пространстве в с точки зрения расстояния по кривой. Мы все еще можем представить себе, что кривая представляет положение движущегося объекта; теперь мы получаем положение объекта в зависимости от того, насколько далеко объект путешествовал.

Пример 13.3.3 Предположим, что ${\bf r}(t)=\langle \cos t,\sin t,0\rangle$. Мы знаем что эта кривая представляет собой окружность радиуса 1. Хотя $t$ может представлять время, он также может в этом случае представлять собой обычный угол между положительная ось $x$ и ${\bf r}(t)$. 2(s/\sqrt2)\over2}+{1\over2}}= \sqrt{{1\over2}+{1\over2}}=1.$$ Таким образом, в общем случае ${\bf r}’$ является единичным касательным вектором.

Имея кривую ${\bf r}(t)$, мы хотели бы иметь возможность измерить при различные точки, как резко он изогнут. Очевидно, это связано с насколько «быстро» касательный вектор меняет направление, поэтому первое предположение может быть, мы можем измерить кривизну с помощью $|{\bf r}»(t)|$. Немного мысль показывает, что это ошибочно; если мы думаем о $t$ как о времени, для например, мы могли бы отслеживать кривую более или менее быстро по прошествии времени. Вторая производная $|{\bf r}»(t)|$ включает это понятие времени, так что оно зависит не только от геометрического свойств кривой, а от того, как быстро мы движемся по кривой.

Пример 13.3.5. Рассмотрим ${\bf r}(t)=\langle \cos t,\sin t,0\rangle$ и ${\bf s}(t)=\langle \cos 2t,\sin 2t,0\rangle$. Оба эти вектора функции представляют единичную окружность в плоскости $x$-$y$, но если $t$ интерпретируется как время, вторая описывает движение объекта в два раза быстрее быстрый как первый. Вычисляя вторые производные, находим $|{\bf r}»(t)|=1$, $|{\bf s}»(t)|=4$. $\квадрат$

Для снятия зависимости от времени используем длину дуги параметризация. Если кривая задается ${\bf r}(s)$, то первая производная ${\bf r}'(s)$ является единичным вектором, т.е. ${\bf r}'(s)={\bf T}(s)$. Теперь вычисляем вторую производную ${\bf r}»(s)={\bf T}'(s)$ и использовать $|{\bf T}'(s)|$ в качестве «официальная» мера кривизна , обычно обозначаемая как $\kappa$.

Пример 13.3.6. Мы видели, что параметризация длины дуги конкретная спираль ${\bf r}(s)= \langle \cos(s/\sqrt2),\sin(s/\sqrt2),s/\sqrt2\rangle$. Вычисление второй производной дает $ {\ bf г} » (с) = \langle -\cos(s/\sqrt2)/2,-\sin(s/\sqrt2)/2,0\rangle$ длины $1/2$. $\квадрат$

Что если нам дана кривая как вектор-функция ${\bf r}(t)$, где $t$ не является длиной дуги? Мы видели, что длина дуги может быть сложной вычислить; к счастью, нам не нужно преобразовывать в длину дуги параметризация для вычисления кривизны. Вместо этого давайте представим, что у нас есть сделали это, поэтому мы нашли $t=g(s)$ и затем сформировали $\шляпа{\bf r}(s)={\bf r}(g(s))$. Первая производная $\hat{\bf r}'(s)$ является единичным касательным вектором, поэтому он совпадает с единичным касательным вектором ${\bf T}(t)={\bf T}(g(s))$. Взяв производную от этого, мы получим $${d\over ds}{\bf T}(g(s))= {\bf T}'(g(s)) g'(s)={\bf T}'(t){dt\ над дс}.$$ Кривизна — это длина этого вектора: $$\каппа = |{\bf T}'(t)||{dt\over ds}|={|{\bf T}'(t)|\over|ds/dt|}= {|{\bf T}'(t)|\over|{\bf r}'(t)|}.$$ (Вспомним, что мы видели, что $ds/dt=|{\bf r}'(t)|$.) Таким образом, мы можем вычислить кривизну, вычислив только производные по $т$; нам не нужно делать преобразование в длину дуги.

Пример 13.3.7 Возвращаясь к спирали, предположим, что мы начинаем с параметризации ${\bf r}(t)=\langle \cos t,\sin t,t\rangle$. Затем ${\bf r}'(t)=\langle -\sin t,\cos t,1\rangle$, $|{\bf r}'(t)|=\sqrt2$ и ${\bf T}(t)=\langle -\sin t,\cos t,1\rangle/\sqrt2$. Затем ${\bf T}'(t)=\langle -\cos t,-\sin t,0\rangle/\sqrt2$ и $|{\bf T}'(t)|=1/\sqrt2$. Наконец, $\kappa=1/\sqrt2/\sqrt2=1/2$, как прежде. $\квадрат$

Пример 13.3.8 Рассмотрим эту окружность радиуса $a$: ${\bf r}(t)=\langle a\cos t,a\sin t,1\rangle$. Затем ${\bf r}'(t)=\langle -a\sin t,a\cos t,0\rangle$, $|{\bf r}'(t)|=a$ и ${\bf T}(t)=\langle -a\sin t,a\cos т,0\угл/а$. Сейчас ${\bf T}'(t)=\langle -a\cos t,-a\sin t,0\rangle/a$ и $|{\bf T}'(t)|=1$. Наконец, $\kappa=1/a$: кривизна круга везде обратна радиусу. Это иногда полезно думать о кривизне как описывающей окружность кривая больше всего напоминает точку. Кривизна спирали в предыдущий пример — $1/2$; это означает, что небольшой кусочек спирали очень похоже на круг радиусом $2$, как показано на рисунок 13.3.1. $\квадрат$ 9{3/2}}.$$ Нарисовав это, мы получим

Высший кривизна возникает там, где кривая имеет самую высокую и самую низкую точки, и действительно на картинке они кажутся наиболее резко изогнутыми части кривой, в то время как кривая представляет собой почти прямую линию посередине между этими точками.