как обозначить и измерить углы, правила
Определение
Геометрия — это раздел математики, который занимается изучением форм и их измерений. Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Определение угла в математике
Определение
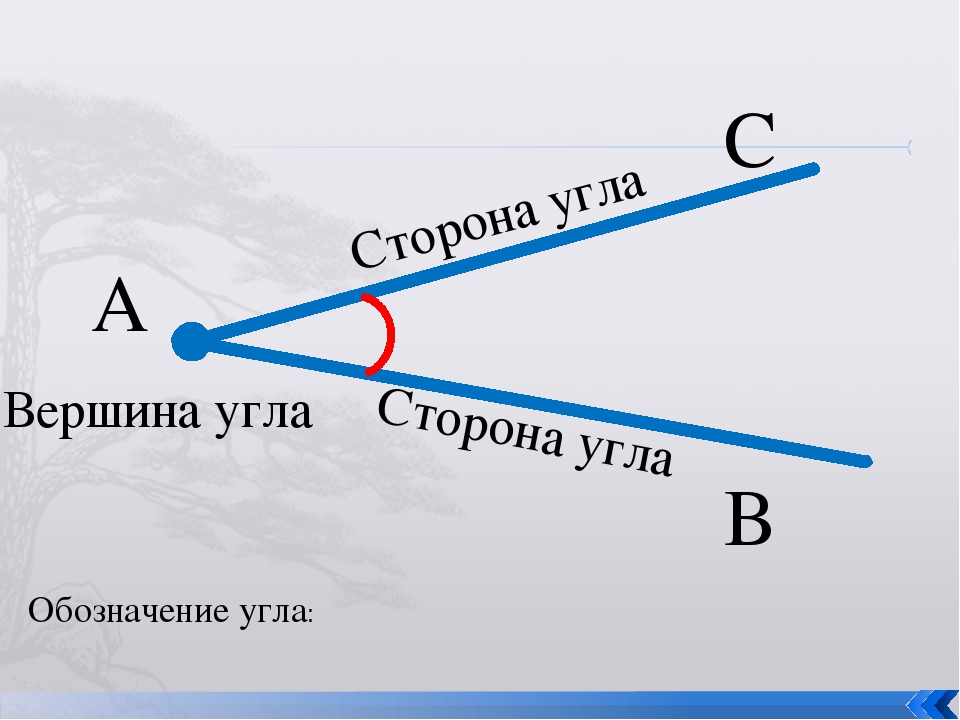
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла – точка, из которой выходят лучи (О).
Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.
Как обозначить углы?
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
- Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д.
- Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
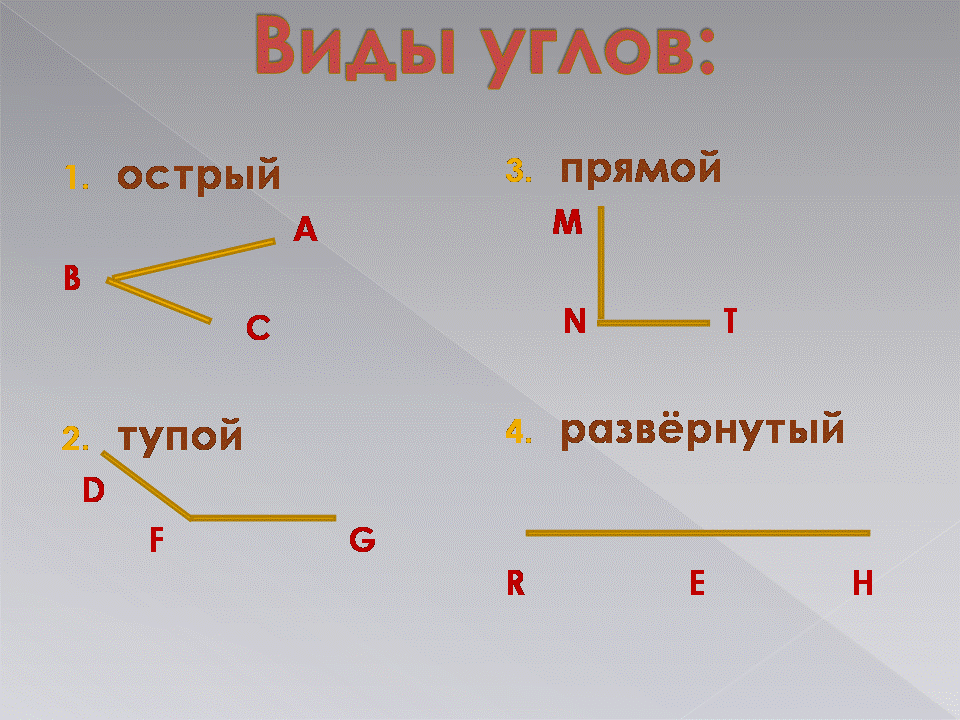
Типы углов
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
- Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.

Прямой угол можно легко наблюдать, так как он образует форму буквы L. - Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
- Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.
Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Углы образованные при пересечении двух прямых
При пересечении двух прямых образуются два вида углов:
- смежные;
- вертикальные.
Смежные углы
Определение
Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол.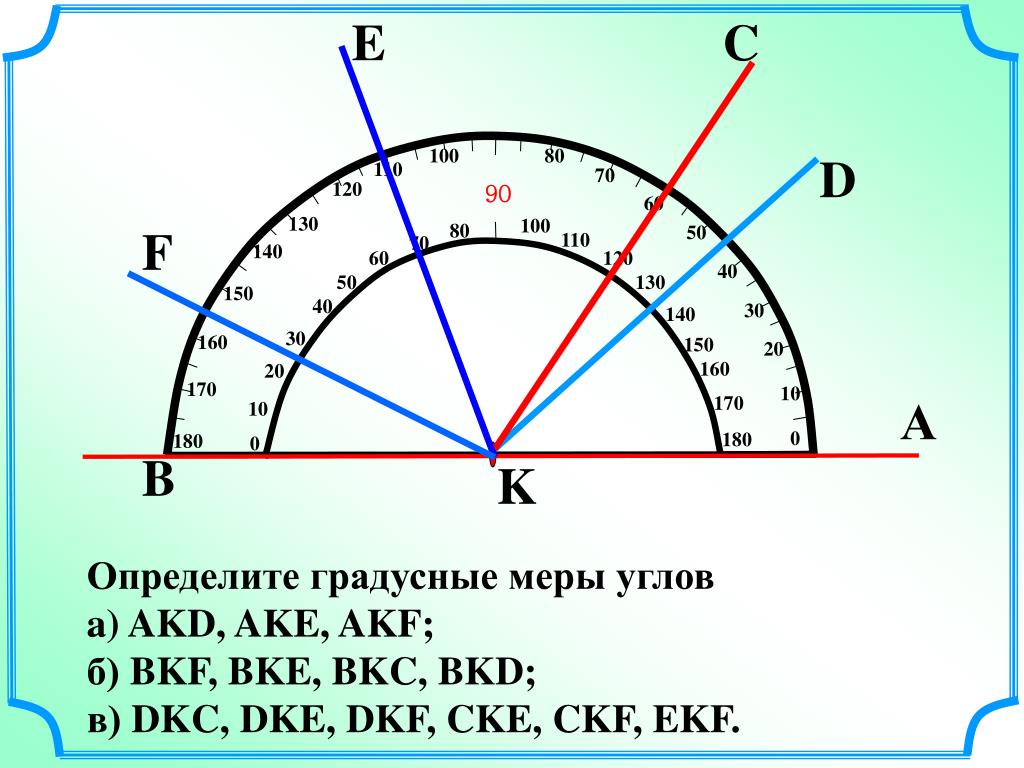
Свойства смежных углов
- Сумма смежных углов равна 180°
- Если оба смежных угла равны между собой, то они являются прямыми.
- В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
- Синусы смежных углов равны.
- Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
Вертикальные углы
Определение
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Пример:
Пары углов 1 и 3; 2 и 4 – являются вертикальными
По свойству вертикальных углов:
\[\angle C O D=\angle A O B\]
\[\angle B O D=\angle A O C\]
Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными
По свойству смежных углов:
\[\angle C O D+\angle D O B=180^{\circ}\]
\[\angle D O B+\angle B O A=180^{\circ}\]
\[\angle B O A+\angle A O C=180^{\circ}\]
\[\angle A O C+\angle C O D=180^{\circ}\]
| Смежные углы | Вертикальные углы |
Два угла с общей стороной и вершиной называются смежными. | Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами. |
| Имеют общую сторону и общую вершину. | Имеют общую вершину, но не имеют общую сторону |
| Смежные углы не всегда равны по величине | Вертикально противоположные углы равны по величине |
Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
\[\angle A_{1} O_{1} B_{1}\] и \[\angle A_{2} O_{2} B_{2}\] полностью совмещаются при наложении следовательно: \[\angle A_{1} O_{1} B_{1}=\angle A_{2} O_{2} B_{2}\]
\[\angle A_{1} O_{1} B_{1}\] и \[ \angle A_{2} O_{2} B_{2}\] не совмещаются при наложении: \[\angle A_{1} O_{1} B_{1} \neq \angle A_{2} O_{2} B_{2}\]
Причем: \[\angle A_{1} O_{1} B_{1}<\angle A_{2} O_{2} B_{2}\]
При этом развернутые углы всегда являются равными.
Совмещение углов \[\angle A B C\] и \[\angle M N K\] происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые.
 Линии могут быть как параллельными, так и непараллельными.
Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:
Градусная мера
Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет \[\left(\frac{1}{360}\right)\] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.
Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов
- 1 градус = 60 минут, обозначаемый как 1° = 60′.
- 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.
Радианная мера
Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица. Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
Вот еще несколько примеров углов: -1 радиан, радиан, \[1 \frac{1}{2}\] радиан, \[-1 \frac{1}{2}\] радиан.
Длина окружности = \[2 \pi r \ldots\] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна \[2 \pi\]. Следовательно, один полный оборот начальной стороны образует в центре угол \[2 \pi\] радиан. Обобщая это, имеем:
В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = \[\frac{l}{r}\] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:
\[\theta=\frac{l}{r}\]
\[l=r \theta\]
Связь между степенью и радианными мерами
По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:
- 360° – по градусной мере
- \[2 \pi\] радиан — в радианах
Следовательно, \[2 \pi\] радиан = 360° ⇒ \[\pi\] радиан = 180°. {\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.
{\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как измерить угол
Для измерения углов используется транспортир:
ТранспортирПопробуем измерить угол \[\angle A O B\]
Шаги для измерения угла \[\angle \mathrm{AOB}\].
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
Далее попробуем измерить этот ∠AOC:
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°
Таким образом, ∠ AOC = 143°
Как построить углы
Используем транспортир для построения углов. Нарисуем угол 50°.
Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.
Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.
Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.
Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.
На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.
Обозначение углов на чертеже
Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.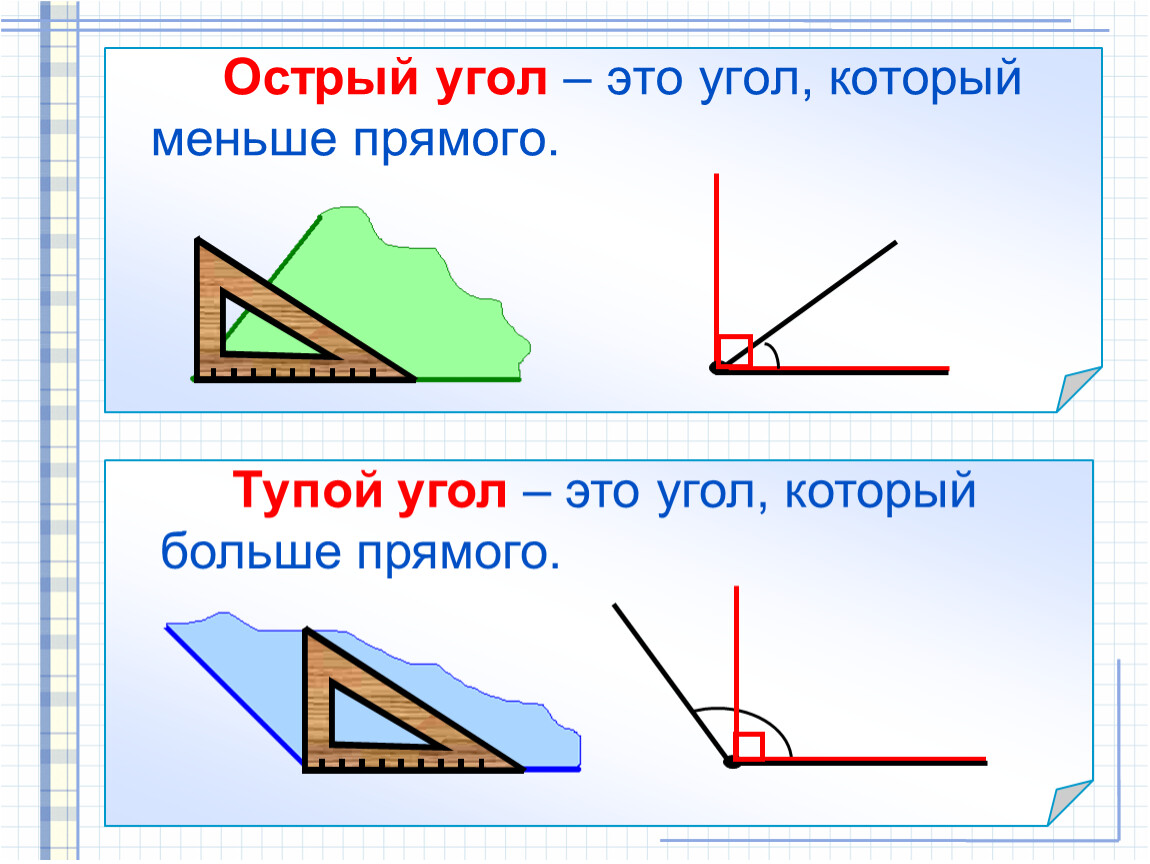
На чертеже запечатлено корректное обозначение острых, равных и неравных углов.
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.
Угол. Градусная мера угла.
Дарим в подарок бесплатный вводный урок!
Понятие угла является одним из наиболее важных определений в геометрии. У́гол — геометрическая фигура, образованная двумя лучами, сторонами угла, выходящими из одной точки, которая называется вершиной угла.
Понятия равенства и суммы углов часто используется в тригонометрии. Например, углы \(15,30,45\) градусов.
Градусы углов
градусная мера угла и наиболее распространенными единицами измерения угла являются градус и радиан. Один градус — это \(\frac{1}{360}\) полного круга. \(90\) градусов — это четверть круга, \(180\) – половина круга (это то, сколько градусов развернутый угол), \(270\) — три четверти круга (это то, сколько градусов тупой угол) и \(360\) это целый круг.
Один градус — это \(\frac{1}{360}\) полного круга. \(90\) градусов — это четверть круга, \(180\) – половина круга (это то, сколько градусов развернутый угол), \(270\) — три четверти круга (это то, сколько градусов тупой угол) и \(360\) это целый круг.
Сколько градусов составляет прямой угол?
Прямой угол равен \(90\) градусов, острый угол больше \(0\) и меньше \(90\) градусов и тупой угол больше \(90\) градусов и меньше \(180\) градусов. Развернутый угол равен \(180\) градусам.
Мы изучаем углы от \(0\)° до \(360\)°, но есть углы больше \(360\)° и отрицательные углы.
Градусы могут быть разделены на минуты и секунды. Каждый градус делится на \(60\) равных частей, которые называются минутами. Так семь с половиной градусов можно сказать \(7\) градусов и \(30\) минут и записать \(7\) ° \(30\)’. Каждая минута делится на \(60\) равных частей, каждая из которых равна одной секунде. Например, \(2\) градуса \(5\) минут \(30\) секунд записывается \(2\)° \(5\)’ \(30\)». Деление градуса на минуты и секунды аналогично делению часа на минуты и секунды времени.
Деление градуса на минуты и секунды аналогично делению часа на минуты и секунды времени.
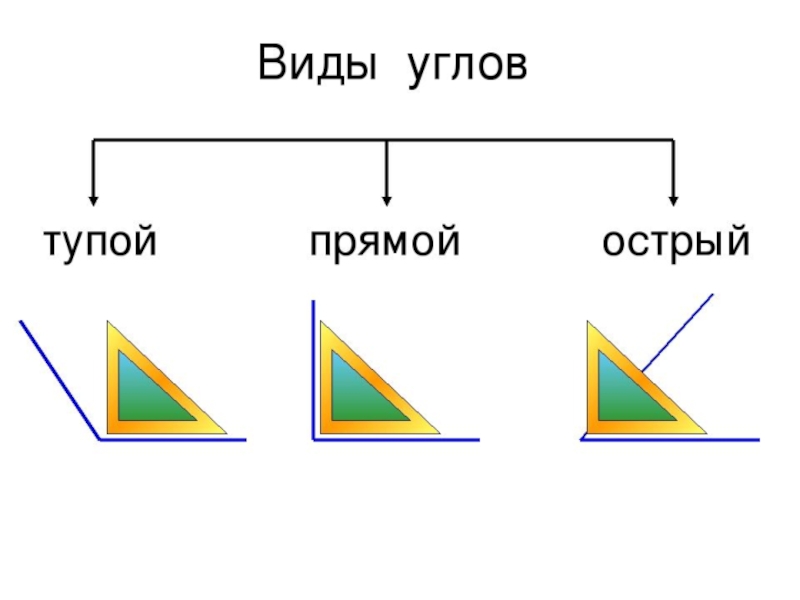
Виды углов
-
Острые углы: углы, чья мера меньше 90 градусов.
-
Прямые углы: углы, чья мера равна 90 градусов.
-
Тупые углы: углы, чья мера больше 90 градусов.
-
Равные углы: углы, чьи меры совпадают.
-
Смежные углы: два угла, которые имеют общую вершину и общую сторону, но не пересекаются внутри этой стороны.
-
Вертикальные углы: два угла, чьи стороны являются противоположными лучами пересекающихся прямых. Вертикальные углы равны между собой.
-
Смежно-вертикальные углы: два угла, один из которых является вертикальным углом, а другой — смежным с ним углом. Смежно-вертикальные углы равны между собой.
Часто задаваемые вопросы:
✅ Что такое угол в математике?
org/Answer»>↪ Угол — это геометрическая фигура, которая образуется двумя лучами, исходящими из общей начальной точки. Начальная точка угла называется вершиной, а лучи — сторонами угла. Измеряется в градусах или радианах.✅ Какие бывают углы?
↪ Углы бывают острые (меньше 90 градусов), прямые (равен 90 градусов), тупые (больше 90 градусов), равные (углы совпадают), смежные (имеют общую вершину и общую сторону, но не пересекаются внутри этой стороны), вертикальные (стороны являются противоположными лучами пересекающихся прямых), смежно-вертикальные (два угла, один из которых является вертикальным углом, а другой — смежным с ним углом).
✅ Как называется угол больше 0, но меньше 90 градусов?
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Угол (математика) — Энциклопедия Нового Света
- Эта статья об углах в геометрии.
В геометрии и тригонометрии угол (или плоский угол ) — это фигура, образованная двумя лучами, имеющими общий конец. Конечная точка называется вершиной угла. Величина угла представляет собой «величину поворота», разделяющую два луча, и может быть измерена путем рассмотрения длины дуги окружности, выметаемой, когда один луч поворачивается вокруг вершины, чтобы совпасть с другим (см. «Измерение углов, » ниже).
Содержание
- 1 История
- 2 Измерение углов
- 2.1 шт.
- 2.2 Положительные и отрицательные углы
- 2.
 3 Приблизительные значения
3 Приблизительные значения
- 3 типа уголка
- 4 Формальное определение
- 4.1 Использование тригонометрических функций
- 4.2 Использование вращения
- 5 Углы между кривыми
- 6 Скалярное произведение и обобщение
- 7 Углы в римановой геометрии
- 8 углов в географии и астрономии
- 9 См. также
- 10 Примечания
- 11 Каталожные номера
- 12 Внешние ссылки
- 13 кредитов
Слово угол происходит от латинского слова angulus, означает «угол». Слово angulus является уменьшительным, примитивная форма которого angus, не встречается в латыни. Родственными словами являются латинское angere, , означающее «сжимать в изгиб» или «задушить», и греческое ἀγκύλος 9.0004 (ankyοs), означает «кривой, искривленный»; оба связаны с корнем PIE *ank-, , означающим «сгибаться» или «поклоняться». [1]
История
Евклид определяет плоский угол как наклон друг к другу в плоскости двух линий, которые встречаются друг с другом и не лежат прямо по отношению друг к другу. Согласно Проклу, угол должен быть либо качеством, либо количеством, либо отношением. Первое понятие использовал Евдем, рассматривавший угол как отклонение от прямой линии; второй — Карпом Антиохийским, который рассматривал его как промежуток или пространство между пересекающимися линиями; Евклид принял третью концепцию, хотя и свои определения прямых, острых и тупых углов.
Согласно Проклу, угол должен быть либо качеством, либо количеством, либо отношением. Первое понятие использовал Евдем, рассматривавший угол как отклонение от прямой линии; второй — Карпом Антиохийским, который рассматривал его как промежуток или пространство между пересекающимися линиями; Евклид принял третью концепцию, хотя и свои определения прямых, острых и тупых углов.
Измерение углов
Угол θ представляет собой частное s и r .Для измерения угла θ дуга окружности с центром в вершине угла рисуется, например, с помощью циркуля. Затем длина дуги s делится на радиус окружности r и, возможно, умножается на константу масштабирования k (которая зависит от выбранных единиц измерения):
- θ = sr (k) {\ displaystyle \ theta = {\ frac {s} {r}} (k)}
Определенное таким образом значение θ не зависит от размера круга: если изменяется длина радиуса, то в той же пропорции изменяется и длина дуги, так что соотношение s / r не меняется.
Во многих геометрических ситуациях углы, которые отличаются точно кратным полному кругу, фактически эквивалентны (не имеет значения, сколько раз линия проходит полный круг, потому что она всегда заканчивается в одном и том же месте). Тем не менее, это не всегда так. Например, при отслеживании кривой, такой как спираль, с использованием полярных координат дополнительный полный оборот приводит к совершенно другой точке кривой.
Единицы измерения
Углы считаются безразмерными, поскольку они определяются как отношение длин. Однако есть несколько единиц, используемых для измерения углов, в зависимости от выбора константы k в приведенной выше формуле.
За заметным исключением радиана, большинство единиц углового измерения определяются таким образом, что один полный круг (т. е. один оборот) равен n единиц для некоторого целого числа n (например, в случае градусов, н = 360). Это эквивалентно установке k = n /2 π в приведенной выше формуле. (Чтобы понять почему, обратите внимание, что один полный круг соответствует дуге, равной длине окружности, которая равна 2 πr , поэтому s = 2 πr . Подставляя, мы получаем θ = ks / r = 2 πk . Но если один полный круг должен иметь числовое угловое значение n , то нам нужно θ = n . Это достигается установкой k = n /2 π .)
(Чтобы понять почему, обратите внимание, что один полный круг соответствует дуге, равной длине окружности, которая равна 2 πr , поэтому s = 2 πr . Подставляя, мы получаем θ = ks / r = 2 πk . Но если один полный круг должен иметь числовое угловое значение n , то нам нужно θ = n . Это достигается установкой k = n /2 π .)
- градус , обозначенный маленьким кругом в верхнем индексе (°), составляет 1/360 полного круга, поэтому один полный круг равен 360°. Одним из преимуществ этой старой шестидесятеричной единицы измерения является то, что многие углы, распространенные в простой геометрии, измеряются целым числом градусов. (Проблема измерения всех «интересных» углов в виде целых чисел, конечно, неразрешима.) Доли градуса могут быть записаны в обычном десятичном представлении (например, 3,5° для трех с половиной градусов), но следующие шестидесятеричные единицы системы «градус-минута-секунда» также используются, особенно для географических координат, а также в астрономии и баллистике:
- минут дуги (или МОА , угловых минут , или просто минут ) составляет 1/60 градуса.
 Он обозначается одним штрихом ( ′ ). Например, 3° 30′ равно 3 + 30/60 градусам или 3,5 градусам. Также иногда используется смешанный формат с десятичными дробями, например, 3° 5,72′ = 3 + 5,72/60 градусов. Морская миля исторически определялась как минута дуги вдоль большого круга Земли.
Он обозначается одним штрихом ( ′ ). Например, 3° 30′ равно 3 + 30/60 градусам или 3,5 градусам. Также иногда используется смешанный формат с десятичными дробями, например, 3° 5,72′ = 3 + 5,72/60 градусов. Морская миля исторически определялась как минута дуги вдоль большого круга Земли. - угловая секунда (или угловая секунда или просто секунд ) составляет 1/60 угловой минуты и 1/3600 градуса. Он обозначается двойным штрихом ( ″ ). Например, 3° 7′ 30″ равно 3 + 7/60 + 30/3600 градусов или 3,125 градуса.
- минут дуги (или МОА , угловых минут , или просто минут ) составляет 1/60 градуса.
- радиан — это угол, образуемый дугой окружности, длина которой равна радиусу окружности ( k = 1 в приведенной выше формуле). Один полный круг равен 2 π радиан, а один радиан равен 180/ π градусов, или примерно 57,2958 градусов. Радиан обозначается аббревиатурой рад, , хотя этот символ часто опускается в математических текстах, где предполагается радиан, если не указано иное.
 Радиан используется практически во всех математических работах, помимо простой практической геометрии, благодаря, например, приятным и «естественным» свойствам, которые демонстрируют тригонометрические функции, когда их аргументы выражены в радианах. Радиан — это (производная) единица измерения угла в системе СИ.
Радиан используется практически во всех математических работах, помимо простой практической геометрии, благодаря, например, приятным и «естественным» свойствам, которые демонстрируют тригонометрические функции, когда их аргументы выражены в радианах. Радиан — это (производная) единица измерения угла в системе СИ.
- мил равно приблизительно равно миллирадиану. Есть несколько определений.
- полный оборот (или оборот , оборот , полный оборот или цикл ) является одним полным оборотом. Оборот и вращение обозначаются rev и rot, соответственно, а просто r в об/мин (оборотов в минуту). 1 полный круг = 360° = 2 π рад = 400 гон = 4 прямых угла.
- Прямой угол составляет 1/4 полного круга. Это единица измерения, используемая в «Элементах» Евклида. 1 прямой угол = 90° = π /2 рад = 100 гон.
- Угол равностороннего треугольника составляет 1/6 часть полной окружности.
 Это устройство использовали вавилоняне, и его особенно легко построить с помощью линейки и циркуля. Градус, угловая минута и угловая секунда являются шестидесятеричными единицами вавилонской единицы измерения. Одна вавилонская единица = 60° = π /3 рад ≈ 1,047197551 рад.
Это устройство использовали вавилоняне, и его особенно легко построить с помощью линейки и циркуля. Градус, угловая минута и угловая секунда являются шестидесятеричными единицами вавилонской единицы измерения. Одна вавилонская единица = 60° = π /3 рад ≈ 1,047197551 рад.
- град , также называемый град , град или угольник составляет 1/400 полного круга, поэтому один полный круг равен 400 градам, а прямой угол равен 10 0 град. Это десятичная единица прямого угла. Километр исторически определялся как сантиметр дуги вдоль большого круга Земли, поэтому километр является десятичным аналогом шестидесятеричной морской мили. Гон используется в основном в триангуляции.
- Точка , используемая в навигации, составляет 1/32 полного круга. Это бинарная субъединица полного круга. Назвать все 32 точки на розе ветров называется «боксирование компаса». 1 точка = 1/8 прямого угла = 11,25° = 12,5 угольника.
- Астрономический часовой угол составляет 1/24 полного круга.
 Шестидесятеричные единицы назывались минут времени и секунд времени (хотя они и являются единицами измерения угла). 1 час = 15° = π /12 рад = 1/6 прямого угла ≈ 16,667 гон.
Шестидесятеричные единицы назывались минут времени и секунд времени (хотя они и являются единицами измерения угла). 1 час = 15° = π /12 рад = 1/6 прямого угла ≈ 16,667 гон.
- Двоичный градус , также известный как двоичный радиан (или брэд ), составляет 1/256 полного круга. Двоичная степень используется в вычислениях, чтобы угол можно было эффективно представить одним байтом.
- градус уклона или уклон на самом деле не является мерой угла (если только он явно не указан в градусах, как это иногда бывает). Вместо этого он равен тангенсу угла, а иногда и синусу. Градиенты часто выражаются в процентах. Для обычно встречающихся небольших значений (менее 5%) уклон уклона приблизительно равен углу в радианах.
Положительные и отрицательные углы
Общепринятое соглашение в математической письменной форме заключается в том, что углы со знаком составляют положительных углов при измерении против часовой стрелки и отрицательных углов при измерении по часовой стрелке от данной линии.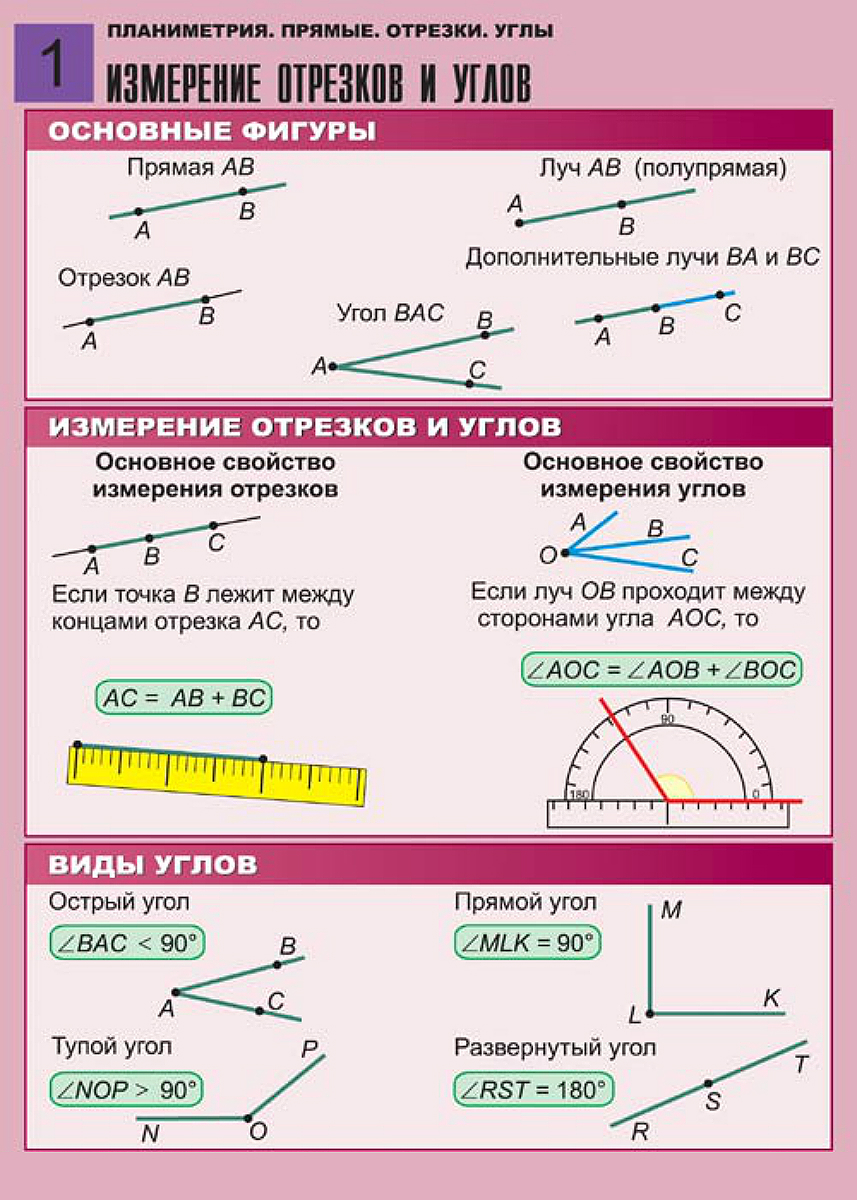 Если линия не указана, можно предположить, что это ось x в декартовой плоскости. Во многих геометрических ситуациях отрицательный угол — θ фактически эквивалентен положительному углу «один полный оборот меньше θ ». Например, поворот по часовой стрелке на 45° (то есть угол -45°) часто фактически эквивалентен повороту против часовой стрелки на 360° — 45° (то есть угол 315°).
Если линия не указана, можно предположить, что это ось x в декартовой плоскости. Во многих геометрических ситуациях отрицательный угол — θ фактически эквивалентен положительному углу «один полный оборот меньше θ ». Например, поворот по часовой стрелке на 45° (то есть угол -45°) часто фактически эквивалентен повороту против часовой стрелки на 360° — 45° (то есть угол 315°).
В трехмерной геометрии «по часовой стрелке» и «против часовой стрелки» не имеют абсолютного значения, поэтому направление положительных и отрицательных углов должно быть определено относительно некоторой точки отсчета, которая обычно представляет собой вектор, проходящий через вершину угла и перпендикулярный плоскости в котором лежат лучи угла.
В навигации азимут измеряется с севера, увеличиваясь по часовой стрелке, поэтому азимут 45 градусов соответствует северо-востоку. Отрицательные азимуты не используются в навигации, поэтому северо-запад составляет 315 градусов.
Приблизительно
- 1° примерно соответствует ширине мизинца на расстоянии вытянутой руки
- 10° примерно соответствует ширине сжатого кулака на расстоянии вытянутой руки.

- 20° примерно соответствует ширине размаха рук на расстоянии вытянутой руки.
Типы уголков
| Прямоугольный. | Острые ( a ), тупые ( b ) и прямые ( c ) углы. Здесь a и b — дополнительные углы. | Угол рефлекса. | Дополнительные углы a и b ( b является дополнением a , а a является дополнением b ). |
- Угол 90° ( π /2 радиана, или четверть полного круга) называется прямым углом .
- Две линии, образующие прямой угол, называются перпендикулярными или ортогональными .
- Углы меньше прямого угла (менее 90°) называются острыми углами («острый» означает «острый»).
- Углы больше прямого угла и меньше двух прямых углов (между 90° и 180°) называются тупыми углами («тупой» означает «тупой»).

- Углы, равные двум прямым углам (180°), называются прямыми углами .
- Углы больше двух прямых, но меньше полной окружности (от 180° до 360°) называются рефлекторными углами .
- Углы, имеющие одинаковую меру, называются равными .
- Два противоположных угла, образованные двумя пересекающимися прямыми линиями, образующими форму, подобную букве «Х», называются 9.0011 вертикальные углы или противоположные углы . Эти углы равны.
- Углы, имеющие общую вершину и ребро, но не имеющие общих внутренних точек, называются смежными углами .
- Два угла, сумма которых составляет один прямой угол (90°), называются дополнительными углами .
- Разность между углом и прямым углом называется дополнением угла.
- Два угла, которые в сумме составляют прямой угол (180°), называются дополнительные углы .
- Разница между углом и прямым углом называется дополнением угла.

- Разница между углом и прямым углом называется дополнением угла.
- Два угла, сумма которых составляет один полный круг (360°), называются дополнительными углами или сопряженными углами .
- Меньший угол в точке, где соединяются два отрезка, называется внутренним углом .
- В евклидовой геометрии сумма внутренних углов треугольника равна π радиан или 180°; меры внутренних углов простого четырехугольника составляют в сумме 2 π радиан, или 360°. В общем, меры внутренних углов простого многоугольника с n сторон в сумме составляют [( n — 2) × π ] радиан, или [( n — 2) × 180]°.
- Угол, дополнительный к внутреннему углу, называется внешним углом .
- Угол между двумя плоскостями (например, двумя соседними гранями многогранника) называется двугранный угол . Его можно определить как острый угол между двумя прямыми, перпендикулярными плоскостям.
- Угол между плоскостью и пересекающейся прямой равен девяноста градусам минус угол между пересекающей прямой и прямой, проходящей через точку пересечения и перпендикулярной плоскости.
 {2}}}}} = {\ frac {y} {x}} = {\ frac {-y} {-x}} = {\ frac {\ sin (\ theta + \ pi)} {\ cos (\тета +\пи )}}} 9{2}}. Угол между двумя векторами будет просто углом поворота, который отображает один на другой. У нас пока нет численного способа определения угла. Для этого мы выбираем вектор (1,0) {\ displaystyle (1,0)}, затем для любой точки M на T {\ displaystyle \ mathbb {T}} на расстоянии θ {\ displaystyle \ theta} от ( 1,0){\displaystyle (1,0)} (на окружности), пусть u→=OM→{\displaystyle {\vec {u}}={\overrightarrow {OM}}}. Если мы назовем rθ{\displaystyle r_{\theta}} вращение, которое преобразует (1,0){\displaystyle (1,0)} в u→{\displaystyle {\vec {u}}}, то [rθ] ↦θ{\displaystyle \left[r _{\theta}\right]\mapsto \theta} — это биекция, что означает, что мы можем идентифицировать любой угол с числом от 0 до 2π{\displaystyle 2\pi}.
{2}}}}} = {\ frac {y} {x}} = {\ frac {-y} {-x}} = {\ frac {\ sin (\ theta + \ pi)} {\ cos (\тета +\пи )}}} 9{2}}. Угол между двумя векторами будет просто углом поворота, который отображает один на другой. У нас пока нет численного способа определения угла. Для этого мы выбираем вектор (1,0) {\ displaystyle (1,0)}, затем для любой точки M на T {\ displaystyle \ mathbb {T}} на расстоянии θ {\ displaystyle \ theta} от ( 1,0){\displaystyle (1,0)} (на окружности), пусть u→=OM→{\displaystyle {\vec {u}}={\overrightarrow {OM}}}. Если мы назовем rθ{\displaystyle r_{\theta}} вращение, которое преобразует (1,0){\displaystyle (1,0)} в u→{\displaystyle {\vec {u}}}, то [rθ] ↦θ{\displaystyle \left[r _{\theta}\right]\mapsto \theta} — это биекция, что означает, что мы можем идентифицировать любой угол с числом от 0 до 2π{\displaystyle 2\pi}.Углы между кривыми
Угол между двумя кривыми определяется как угол между касательными A и B на PУгол между прямой и кривой (смешанный угол) или между двумя пересекающимися кривых (криволинейный угол) определяется как угол между касательными в точке пересечения.
 Частным случаям давались различные названия (теперь редко, если вообще когда-либо) давались: амфикиртик (греч. ἀμφί , с обеих сторон, κυρτόσ , выпуклый) или циссоидальный (гр. κισσόσ , плющ), двояковыпуклый; ксистроидальный или систроидальный (гр. ξυστρίσ , инструмент для шабрения), вогнуто-выпуклый; амфицельный (гр. κοίλη , впадина) или angulus lunularis , двояковогнутый.
Частным случаям давались различные названия (теперь редко, если вообще когда-либо) давались: амфикиртик (греч. ἀμφί , с обеих сторон, κυρτόσ , выпуклый) или циссоидальный (гр. κισσόσ , плющ), двояковыпуклый; ксистроидальный или систроидальный (гр. ξυστρίσ , инструмент для шабрения), вогнуто-выпуклый; амфицельный (гр. κοίλη , впадина) или angulus lunularis , двояковогнутый.Скалярное произведение и обобщение
В евклидовой плоскости угол θ между двумя векторами u и v связан с их скалярным произведением и их длинами по формуле
- ты⋅v=cos(θ) ‖u‖ ‖v‖.{\ Displaystyle \ mathbf {u} \ cdot \ mathbf {v} = \ cos (\ theta) \ \|\ mathbf {u} \ |\ \|\mathbf {v} \|.}
Это позволяет определить углы в любом вещественном пространстве внутреннего произведения, заменив евклидово скалярное произведение · внутренним произведением гильбертова пространства <·,·>.

Углы в римановой геометрии
В римановой геометрии метрический тензор используется для определения угла между двумя касательными. Где U и V касательные векторы и 9{j}\right|}}}.}
Углы в географии и астрономии
В географии мы указываем местоположение любой точки на Земле, используя Географическую систему координат . Эта система определяет широту и долготу любого места с точки зрения углов, лежащих в центре Земли, с использованием экватора и (обычно) меридиана Гринвича в качестве ориентиров.
В астрономии мы аналогичным образом задаем данную точку на небесной сфере, используя любой из нескольких Астрономические системы координат , где ссылки варьируются в зависимости от конкретной системы.
Астрономы также могут измерить угловое расстояние двух звезд, вообразив две линии, проходящие через центр Земли, каждая из которых пересекает одну из звезд. Угол между этими линиями можно измерить, и он представляет собой угловое расстояние между двумя звездами.

Астрономы также измеряют видимый размер объектов. Например, полная луна имеет угловое измерение примерно 0,5 °, если смотреть с Земли. Можно сказать: «Луна образует угол в полградуса». Формула малого угла может использоваться для преобразования такого углового измерения в отношение расстояния к размеру.
См. также
- Круг
- Квадрат (геометрия)
- Треугольник
Примечания
- ↑ Джонатан Слокум. 2007. Предварительный индоевропейский лексикон: данные Pokorny PIE. Центр лингвистических исследований Техасского университета в Остине . Проверено 13 ноября 2007 г.
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Coxeter, HSM 1989. Introduction to Geometry. Библиотека классики Wiley. Нью-Йорк: Уайли. ISBN 0471504580.
- Эрнисс, Кэтлин и Дон О’Коннор. 1999. Простая геометрия. Торранс, Калифорния: Публикации Фрэнка Шаффера.
 ISBN 0768202620 .
ISBN 0768202620 .
- Гибсон, К.Г. 2004. Элементарная евклидова геометрия: введение для студентов. Кембридж, Великобритания: Издательство Кембриджского университета. ISBN 0521834481.
Внешние ссылки
Все ссылки получены 19 июня 2021 г.
- Биссектрисы углов четырехугольника в точке пересечения.
- Построение треугольника по биссектрисам его углов в точке пересечения узла.
- Страницы определения угла с интерактивными апплетами.
- Различные угловые конструкции с компасом и линейкой Анимированные демонстрации.
Кредиты
Энциклопедия Нового Света авторов и редакторов переписали и дополнили статьи Википедии в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Кредит должен соответствовать условиям этой лицензии, которая может ссылаться как на Энциклопедия Нового Света участников и самоотверженных добровольных участников Фонда Викимедиа.
 Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:- Угол история
История этой статьи с момента ее импорта в New World Encyclopedia :
- История «Угла (математика)»
Примечание. На использование отдельных изображений, которые лицензируются отдельно, могут распространяться некоторые ограничения.
Углы – Математика GCSE Revision – Повторение математики
Углы измеряются в градусах, пишется °. Максимальный угол составляет 360°. Это угол вокруг точки. Половина этого угла составляет угол на прямой, который равен 180°.
В приведенном ниже видео показано, как вычислять смежные углы, смежные углы, внутренние углы и дополнительные углы.
youtube.com/embed/KgNN2ZJPMqY» title=»YouTube video player»>Смежные углы
Прямые AB и CD параллельны друг другу (отсюда » на прямых).
a и d известны как вертикально противоположных углов. Вертикально противоположные углы равны. (b и c, e и h, f и g также вертикально противоположны).
g и c соответствующие углы . Соответствующие углы равны. (h и d, f и b, e и a также соответствуют).
d и e равны альтернативные углы . Альтернативные углы равны. (c и f также чередуются). Альтернативные углы образуют форму «Z» и иногда называются «Z-углами».
a и b являются смежными углами . Смежные углы в сумме дают 180 градусов. (d и c, c и a, d и b, f и e, e и g, h и g, h и f также являются смежными).
d и f внутренние углы . В сумме они составляют 180 градусов (e и c также являются внутренними).
Любые два угла, сумма которых составляет 180 градусов, называются дополнительные углы .

Сумма углов треугольника
Используя некоторые из приведенных выше результатов, мы можем доказать, что сумма трех углов внутри любого треугольника всегда составляет 180 градусов.
Если у нас есть треугольник, вы всегда можете провести две параллельные линии следующим образом:
Теперь мы знаем, что альтернативных угла равны. Следовательно, два угла, обозначенные х, равны. Кроме того, два угла, обозначенные y, равны.
Мы знаем, что x, y и z вместе составляют 180 градусов, потому что вместе они представляют собой просто угол вокруг прямой. Таким образом, три угла треугольника должны составлять в сумме 180 градусов.
Сумма углов четырехугольника
Четырехугольник – это фигура с 4 сторонами.
Теперь, когда мы знаем сумму углов треугольника, мы можем вычислить сумму углов четырехугольника.
Для любого четырехугольника можно провести диагональную линию, чтобы разделить его на два треугольника.
 Каждый треугольник имеет сумму углов 180 градусов. Следовательно, сумма углов четырехугольника равна 360 градусов.
Каждый треугольник имеет сумму углов 180 градусов. Следовательно, сумма углов четырехугольника равна 360 градусов.Внешние углы
Внешние углы фигуры — это углы, которые вы получите, если удлините стороны. Показаны внешние углы шестиугольника:
Многоугольник — это фигура с прямыми сторонами. Все внешние углы многоугольника в сумме дают 360°. потому что, если вы сложите их все вместе, они образуют угол вокруг точки:
Следовательно, если у вас есть правильный многоугольник (другими словами, где все стороны имеют одинаковую длину и все углы одинаковы) , каждый из внешних углов будет иметь размер 360 ÷ количество сторон. Так, например, каждый из внешних углов шестиугольника равен 360/6 = 60°.
Внутренние углы
внутренних угла формы — это углы внутри нее. Если вы знаете размер внешнего угла, вы можете определить размер внутреннего угла рядом с ним, потому что они дадут в сумме 180 ° (поскольку вместе они составляют угол на прямой).


 Линии могут быть как параллельными, так и непараллельными.
Линии могут быть как параллельными, так и непараллельными. 3 Приблизительные значения
3 Приблизительные значения Он обозначается одним штрихом ( ′ ). Например, 3° 30′ равно 3 + 30/60 градусам или 3,5 градусам. Также иногда используется смешанный формат с десятичными дробями, например, 3° 5,72′ = 3 + 5,72/60 градусов. Морская миля исторически определялась как минута дуги вдоль большого круга Земли.
Он обозначается одним штрихом ( ′ ). Например, 3° 30′ равно 3 + 30/60 градусам или 3,5 градусам. Также иногда используется смешанный формат с десятичными дробями, например, 3° 5,72′ = 3 + 5,72/60 градусов. Морская миля исторически определялась как минута дуги вдоль большого круга Земли.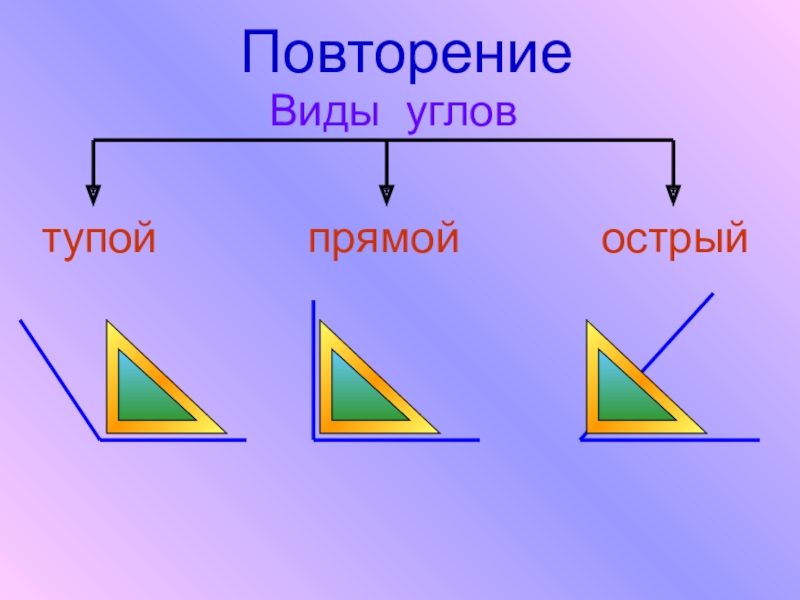 Радиан используется практически во всех математических работах, помимо простой практической геометрии, благодаря, например, приятным и «естественным» свойствам, которые демонстрируют тригонометрические функции, когда их аргументы выражены в радианах. Радиан — это (производная) единица измерения угла в системе СИ.
Радиан используется практически во всех математических работах, помимо простой практической геометрии, благодаря, например, приятным и «естественным» свойствам, которые демонстрируют тригонометрические функции, когда их аргументы выражены в радианах. Радиан — это (производная) единица измерения угла в системе СИ.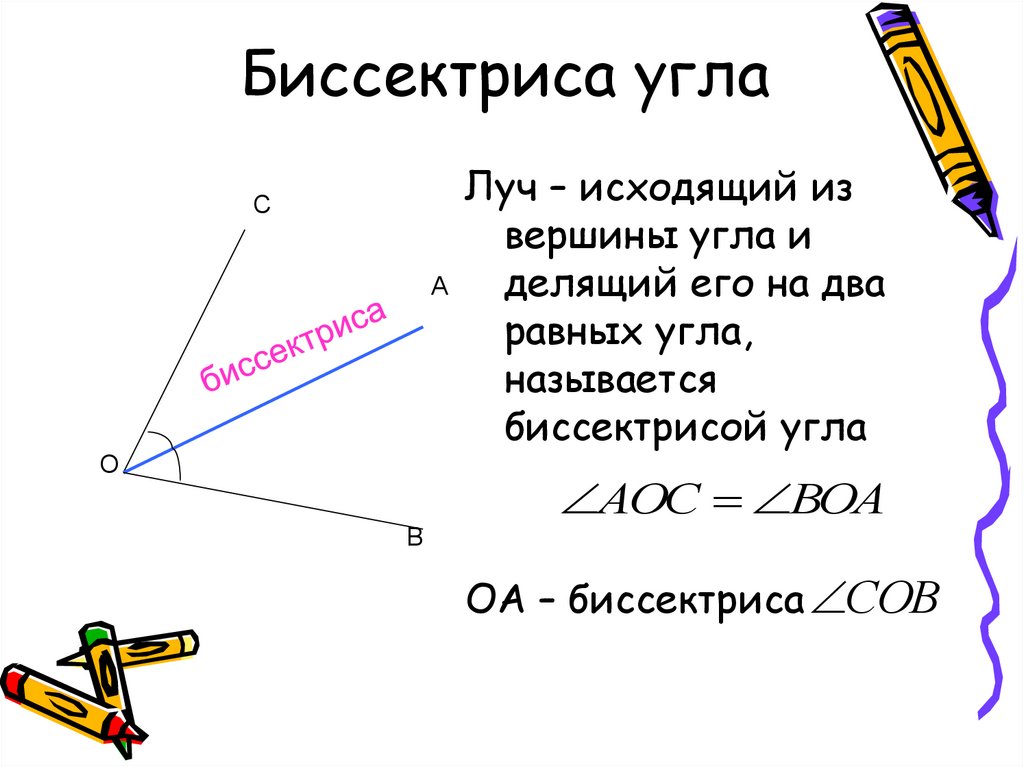 Это устройство использовали вавилоняне, и его особенно легко построить с помощью линейки и циркуля. Градус, угловая минута и угловая секунда являются шестидесятеричными единицами вавилонской единицы измерения. Одна вавилонская единица = 60° = π /3 рад ≈ 1,047197551 рад.
Это устройство использовали вавилоняне, и его особенно легко построить с помощью линейки и циркуля. Градус, угловая минута и угловая секунда являются шестидесятеричными единицами вавилонской единицы измерения. Одна вавилонская единица = 60° = π /3 рад ≈ 1,047197551 рад.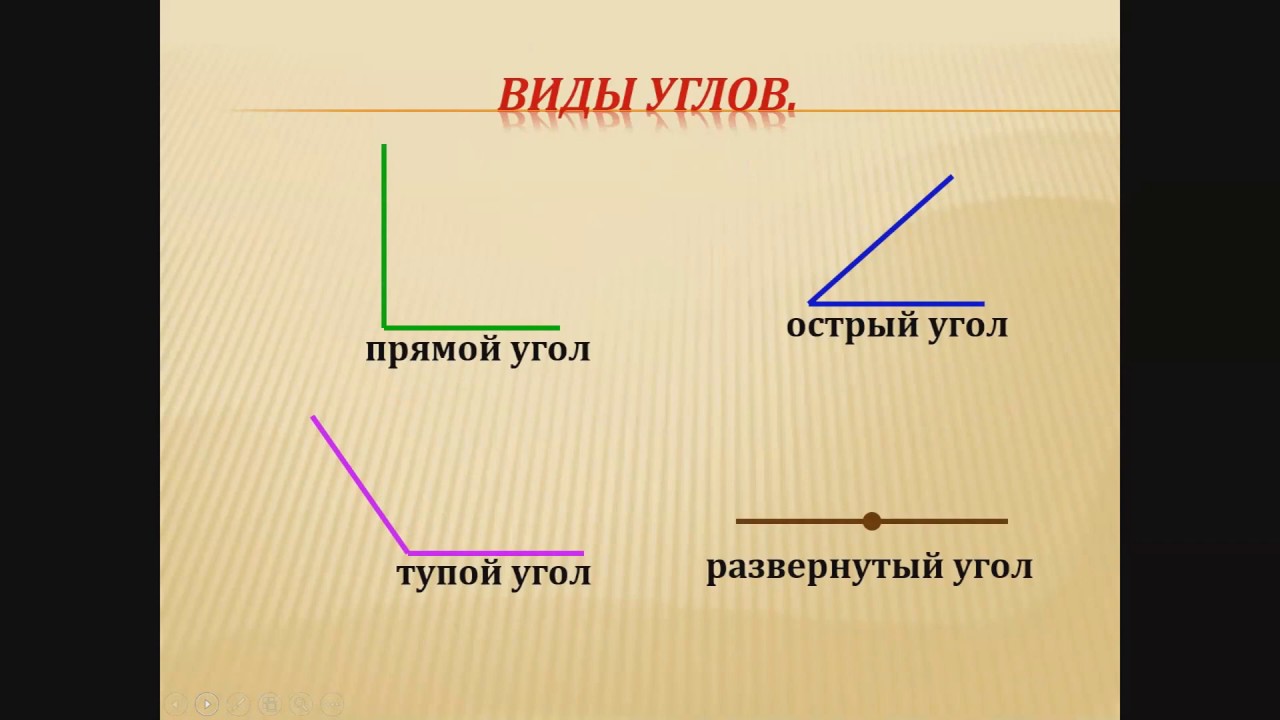 Шестидесятеричные единицы назывались минут времени и секунд времени (хотя они и являются единицами измерения угла). 1 час = 15° = π /12 рад = 1/6 прямого угла ≈ 16,667 гон.
Шестидесятеричные единицы назывались минут времени и секунд времени (хотя они и являются единицами измерения угла). 1 час = 15° = π /12 рад = 1/6 прямого угла ≈ 16,667 гон.


 {2}}}}} = {\ frac {y} {x}} = {\ frac {-y} {-x}} = {\ frac {\ sin (\ theta + \ pi)} {\ cos (\тета +\пи )}}} 9{2}}. Угол между двумя векторами будет просто углом поворота, который отображает один на другой. У нас пока нет численного способа определения угла. Для этого мы выбираем вектор (1,0) {\ displaystyle (1,0)}, затем для любой точки M на T {\ displaystyle \ mathbb {T}} на расстоянии θ {\ displaystyle \ theta} от ( 1,0){\displaystyle (1,0)} (на окружности), пусть u→=OM→{\displaystyle {\vec {u}}={\overrightarrow {OM}}}. Если мы назовем rθ{\displaystyle r_{\theta}} вращение, которое преобразует (1,0){\displaystyle (1,0)} в u→{\displaystyle {\vec {u}}}, то [rθ] ↦θ{\displaystyle \left[r _{\theta}\right]\mapsto \theta} — это биекция, что означает, что мы можем идентифицировать любой угол с числом от 0 до 2π{\displaystyle 2\pi}.
{2}}}}} = {\ frac {y} {x}} = {\ frac {-y} {-x}} = {\ frac {\ sin (\ theta + \ pi)} {\ cos (\тета +\пи )}}} 9{2}}. Угол между двумя векторами будет просто углом поворота, который отображает один на другой. У нас пока нет численного способа определения угла. Для этого мы выбираем вектор (1,0) {\ displaystyle (1,0)}, затем для любой точки M на T {\ displaystyle \ mathbb {T}} на расстоянии θ {\ displaystyle \ theta} от ( 1,0){\displaystyle (1,0)} (на окружности), пусть u→=OM→{\displaystyle {\vec {u}}={\overrightarrow {OM}}}. Если мы назовем rθ{\displaystyle r_{\theta}} вращение, которое преобразует (1,0){\displaystyle (1,0)} в u→{\displaystyle {\vec {u}}}, то [rθ] ↦θ{\displaystyle \left[r _{\theta}\right]\mapsto \theta} — это биекция, что означает, что мы можем идентифицировать любой угол с числом от 0 до 2π{\displaystyle 2\pi}. Частным случаям давались различные названия (теперь редко, если вообще когда-либо) давались: амфикиртик (греч. ἀμφί , с обеих сторон, κυρτόσ , выпуклый) или циссоидальный (гр. κισσόσ , плющ), двояковыпуклый; ксистроидальный или систроидальный (гр. ξυστρίσ , инструмент для шабрения), вогнуто-выпуклый; амфицельный (гр. κοίλη , впадина) или angulus lunularis , двояковогнутый.
Частным случаям давались различные названия (теперь редко, если вообще когда-либо) давались: амфикиртик (греч. ἀμφί , с обеих сторон, κυρτόσ , выпуклый) или циссоидальный (гр. κισσόσ , плющ), двояковыпуклый; ксистроидальный или систроидальный (гр. ξυστρίσ , инструмент для шабрения), вогнуто-выпуклый; амфицельный (гр. κοίλη , впадина) или angulus lunularis , двояковогнутый.
 ISBN 0768202620 .
ISBN 0768202620 . Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
 Каждый треугольник имеет сумму углов 180 градусов. Следовательно, сумма углов четырехугольника равна 360 градусов.
Каждый треугольник имеет сумму углов 180 градусов. Следовательно, сумма углов четырехугольника равна 360 градусов.