Построение графика функции по точкам. Практикум по математическому анализу. Урок 6
Высшая математика / Практикум по математическому анализу
Наглядное графическое изображение функциональной зависимости между двумя переменными
и можно получить, рассматривая значения этих переменных как координаты точек на плоскости.
Графиком функции, заданной уравнением , называется совокупность всех точек плоскости, координаты которых удовлетворяют этому уравнению.
Обычно график функции представляет некоторую плоскую линию.
Построение графика аналитически заданной функции по точкам выполняется в следующем порядке:
1) по данному аналитическому выражению функции составляется таблица соответствующих друг другу значений переменных;
2) выбирается система координат с подходящими единицами масштаба для каждой переменной.
Обычно применяется прямоугольная система координат и одна общая единица масштаба для обеих координатных осей;
3) строятся точки, координатами которых являются соответствующие друг другу значения аргумента и функции, содержащиеся в таблице;
4) полученные точки соединяются плавной линией.
Построенный этим способом график функции будет тем точнее, чем больше значений переменных содержится в таблице, чем больше точек будет нанесено на координатную плоскость.
Построение графика функции упрощается, если она является четной, нечетной или периодической. График четной функции симметричен относительно оси ; график нечетной функции симметричен относительно начала координату график периодической функции получается путем повторения части ее графика, соответствующей одному периоду.
Пример 1. Построить графики функций:
1) на отрезке [—2; 4];
2) на отрезке [—5; 5];
3) на отрезке ;
4) на отрезке [-6; 5];
5) между точками пересечения с осью .
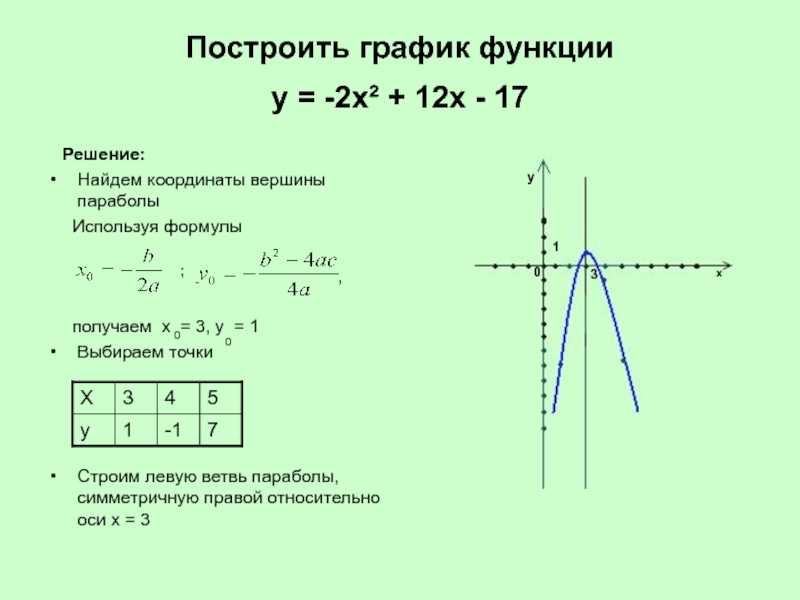
Решение. 1) В условии задачи указано, что независимой переменной можно придавать только значения, заключенные на отрезке [—2; 4]. Учитывая это, составим следующую таблицу, беря для простоты только целые значения и вычисляя из данного уравнения соответствующие значения :
Рис.1
Введем прямоугольную систему координат, как показано на рис. 1, с одинаковыми единицами масштаба, которые указаны числовыми пометками на координатных осях.
Построим точки, откладывая содержащиеся в таблице значения аргумента
по оси абсцисс, а значения функции по оси ординат. Соединим полученные точки плавной кривой, которая и будет графиком данной функции. Эта кривая называется параболой.
Вообще графиком всякой квадратной функции является парабола, ось симметрии которой параллельна оси .
2) Функция — нечетная, так как для нее . Для значений аргумента, отличающихся только по знаку, значения нечетной функции будут также отличаться только по знаку. Поэтому при составлении таблицы здесь достаточно вычислить изданного уравнения значения функции только для положительных значений аргумента. Значения функции для отрицательных значений аргумента получим путем простои перемены знаков.
Для значений аргумента, отличающихся только по знаку, значения нечетной функции будут также отличаться только по знаку. Поэтому при составлении таблицы здесь достаточно вычислить изданного уравнения значения функции только для положительных значений аргумента. Значения функции для отрицательных значений аргумента получим путем простои перемены знаков.
Выберем систему координат с одинаковыми масштабами на координатных осях (рис.2).
Построим точки для каждой пары числовых значений и , которые содержатся в строках таблицы. Соединяя эти точки плавной кривой, получим график, симметричный относительно начала координат.
Рис.2
3) Функция
является четной, так как при перемене знака у любого значения аргумента значение этой функции не изменяется, . Поэтому здесь при составлении таблицы достаточно вычислить значения функции только для положительных значений аргумента; значения функции для отрицательных значений аргумента будут те же.
Составив таблицу, замечаем, что значения аргумента есть числа 1-го порядка, тогда как значения функции — числа 3-го порядка. Поэтому для построения соответствующих точек берем разные масштабы абсцисс и ординат; они показаны числовыми пометками на координатных осях (рис.3).
Рис.3
График данной четной функции симметричен относительно оси ординат.
4) Составим таблицу значений функции
для значений аргумента , заключенных на отрезке [—6; 5].
Затем строим точки и, соединяя их сплошной линией, получим искомый график (рис.4).
Данная функция не является четной или нечетной. Поэтому ее график не симметричен ни относительно оси , ни относительно начала координат.
Рис.4
5) Абсциссы точек пересечения графика данной функции с осью
найдем из данного уравнения, зная, что в этих точках ордината . При , откуда . Далее составляем таблицу значений данной четной функции на отрезке [—4; 4] и строим ее график (рис.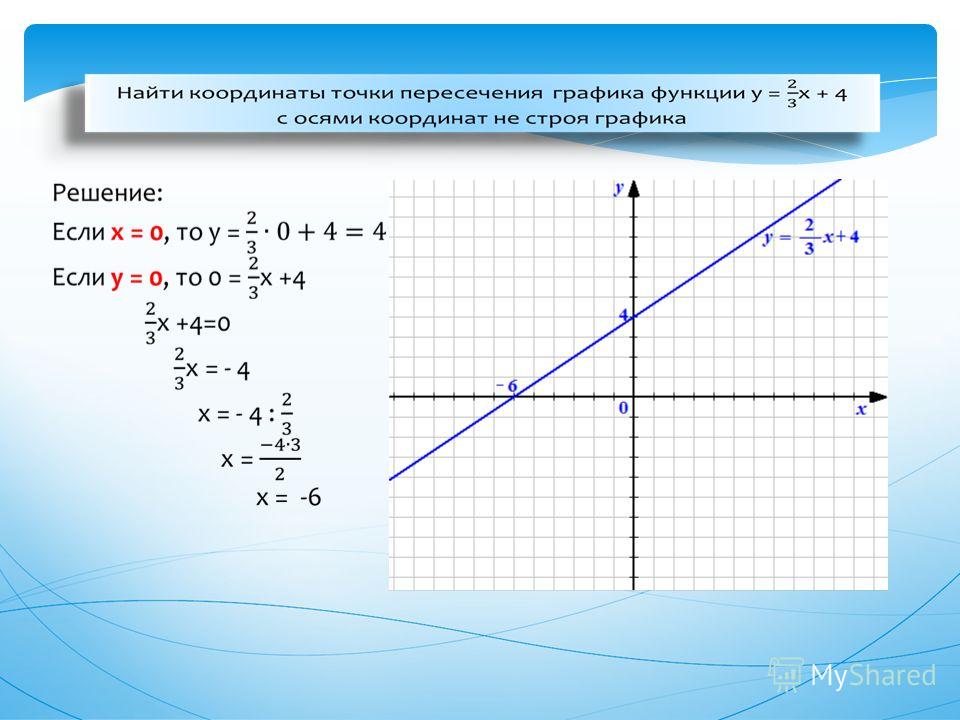 5).
5).
Рис.5
Когда
приближается к нулю слева или справа, значения функции и ординаты ее графика неограниченно возрастают. При функция не имеет никакого числового значения, ее график состоит из двух отдельных бесконечных ветвей.
Тегиграфик нечетной функцииграфик функцииграфик четной функциипостроить график функцииПодбор полинома по заданным точкам
|
|
|
||||||||||||||||||||||||||||
Калькулятор экспоненциальной функции — MathCracker.
 com
Алгебра
Решатели
com
Алгебра
Решатели
Инструкции: Используйте этот пошаговый калькулятор экспоненциальной функции, чтобы найти функцию, описывающую экспоненциальную функцию, которая проходит через две заданные точки на плоскости XY. Вам необходимо указать точки \((t_1, y_1)\) и \((t_2, y_2)\), и этот калькулятор оценит соответствующую экспоненциальную функцию и предоставит ее график.
Первый y (\(f(t_1)\)) =
Второй t (\(t_2\)) =
Второй год: (\(f(t_2)\)) =
Баллы для оценки (необязательно. {k t_2}} \]
{k t_2}} \]
Как рассчитать экспоненциальный рост?
Это не всегда рост. Действительно, если параметр \(k\) положительный, то у нас есть экспоненциальный рост, но если параметр \(k\) отрицательный, то у нас есть экспоненциальный спад.
Параметр \(k\) будет равен нулю, только если \(y_1 = y_2\) (две точки имеют одинаковую высоту).
Для получения информации об экспоненциальном поведении вы можете проверить наш
калькулятор экспоненциального роста
и
калькулятор экспоненциального распада
, которые используют определенные параметры для такого экспоненциального поведения.
Калькулятор алгебры Алгебра Решатель Базовый пакет алгебры Калькулятор экспоненциальной функции Калькулятор экспоненциальной функции с двух точек зрения калькулятор экспоненциальной функции с учетом баллов
Расчет I — критические точки
Онлайн-заметки Пола
Главная
/
Исчисление I
/
Применение производных
/ Критические точки
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-2: Критические точки
Критические точки будут появляться на протяжении большей части этой главы, поэтому нам сначала нужно определить их и поработать с несколькими примерами, прежде чем переходить к разделам, в которых они используются.
Определение
Мы говорим, что \(x = c\) является критической точкой функции \(f\left( x \right)\), если \(f\left( c \right)\) существует и если верно любое из следующих утверждений.
\[f’\влево(c\вправо) = 0\hspace{0,5 дюйма}{\mbox{OR}}\hspace{0,5in}f’\влево(c\вправо)\,\,\,{\mbox {не существует}}\]
Обратите внимание, что мы требуем, чтобы \(f\left( c \right)\) существовало, чтобы \(x = c\) действительно было критической точкой. Это важный момент, которым часто пренебрегают. На самом деле это говорит о том, что все критические точки должны находиться в области определения функции. Если точка не находится в области определения функции, то она не является критической точкой.
Это важный момент, которым часто пренебрегают. На самом деле это говорит о том, что все критические точки должны находиться в области определения функции. Если точка не находится в области определения функции, то она не является критической точкой.
Также обратите внимание, что на данный момент мы работаем только с действительными числами, поэтому любые комплексные числа, которые могут возникнуть при нахождении критических точек (а они иногда будут возникать), будут игнорироваться. Есть части исчисления, которые работают немного по-другому при работе с комплексными числами, и поэтому в первом классе исчисления, таком как этот, мы игнорируем комплексные числа и работаем только с действительными числами. Расчет с комплексными числами выходит за рамки этого курса и обычно преподается на курсах математики более высокого уровня. 92}\влево({5x — 3}\вправо)\влево({x+5}\вправо) = 0\]
Поскольку это факторизованная форма производной, довольно легко определить три критические точки. Они есть,
Они есть,
\[x = — 5,\,\,\,\,\,\,x = 0,\,\,\,\,\,\,x = \frac{3}{5}\]
Полиномы обычно представляют собой довольно простые функции для нахождения критических точек при условии, что степень не становится настолько большой, что возникают проблемы с поиском корней производной. 9{\ гидроразрыва {1} {3}}}}} \]
Нам нужно быть осторожными с этой проблемой. Столкнувшись с отрицательным показателем степени, часто лучше исключить знак минус в показателе степени, как мы сделали выше. На самом деле это не обязательно, но иногда это может облегчить нашу жизнь, если мы это сделаем.
Обратите также внимание, что удаление отрицательного показателя степени во втором члене позволяет нам правильно определить, почему \(t = 0\) является критической точкой для этой функции. Как только мы переместим второй член в знаменатель, мы ясно увидим, что производная не существует в \(t = 0\), и поэтому это будет критическая точка. Если вы не избавитесь от отрицательного показателя степени во втором члене, многие люди неправильно заявят, что \(t = 0\) является критической точкой, потому что производная равна нулю в \(t = 0\). Хотя это может показаться глупой точкой, в конце концов, в каждом случае \(t = 0\) идентифицируется как критическая точка, это
иногда важно знать, почему точка является критической точкой. Фактически, через пару разделов мы увидим факт, который работает только для критических точек, в которых производная равна нулю. 9{\ гидроразрыва {1} {3}}}}} \]
Если вы не избавитесь от отрицательного показателя степени во втором члене, многие люди неправильно заявят, что \(t = 0\) является критической точкой, потому что производная равна нулю в \(t = 0\). Хотя это может показаться глупой точкой, в конце концов, в каждом случае \(t = 0\) идентифицируется как критическая точка, это
иногда важно знать, почему точка является критической точкой. Фактически, через пару разделов мы увидим факт, который работает только для критических точек, в которых производная равна нулю. 9{\ гидроразрыва {1} {3}}}}} \]
Обратите внимание, что у нас все еще есть \(t = 0\) в качестве критической точки. Выполнение такого объединения никогда не должно терять критические точки, это делается только для того, чтобы помочь нам найти их. Как мы видим, теперь стало намного проще быстро определить, где производная будет равна нулю. Напомним, что рациональное выражение будет равно нулю только в том случае, если его числитель равен нулю (и, конечно, при условии, что знаменатель в этот момент не равен нулю). 2} — w — 6 = \left( {w — 3} \right)\left( {w + 2} \right) = 0\]
2} — w — 6 = \left( {w — 3} \right)\left( {w + 2} \right) = 0\]
Мы не стали возводить это в квадрат, так как если это ноль, то ноль в квадрате по-прежнему будет нулем, а если он не равен нулю, то возведение в квадрат не сделает его равным нулю.
Отсюда видно, что производная не будет существовать при \(w = 3\) и \(w = — 2\). Однако это НЕ критические точки, так как в этих точках функция также не будет существовать. Напомним, что для того, чтобы точка была критической, функция должна действительно существовать в этой точке.
В этот момент мы должны быть осторожны. Числитель не учитывается, но это не означает, что нет критических точек, в которых производная равна нулю. Мы можем использовать формулу квадрата для числителя, чтобы определить, равна ли дробь в целом нулю. 92} — 4\влево( 1 \вправо)\влево( { — 1} \вправо)} }}{{2\влево( 1 \вправо)}} = \frac{{ — 14 \pm \sqrt {200} }}{2} = \frac{{ — 14 \pm 10\sqrt 2 }}{2} = — 7 \pm 5\sqrt 2 \]
Итак, мы получаем две критические точки. Кроме того, это не «хорошие» целые числа или дроби. Это будет происходить при случае. Не зацикливайтесь на ответах, которые всегда должны быть «хорошими». Часто это не так.
Кроме того, это не «хорошие» целые числа или дроби. Это будет происходить при случае. Не зацикливайтесь на ответах, которые всегда должны быть «хорошими». Часто это не так.
Обратите внимание, что мы используем только действительные числа для критических точек. Итак, если бы при решении квадратного числа в числителе мы получили комплексное число, эти точки не считались бы критическими.
Подводя итог, у нас есть две критические точки. Они есть,
\[w = — 7 + 5\sqrt 2 ,\,\,\,\,w = — 7 — 5\sqrt 2 \]
Опять же, помните, что, хотя производная не существует в точках \(w = 3\) и \(w = — 2\), не существует и функции, поэтому эти две точки не являются критическими для этой функции.
В предыдущем примере нам пришлось использовать квадратичную формулу для определения некоторых потенциальных критических точек. Мы знаем, что иногда мы получаем комплексные числа из квадратичной формулы. Просто помните, что, как упоминалось в начале этого раздела, когда это происходит, мы игнорируем возникающие комплексные числа.
Просто помните, что, как упоминалось в начале этого раздела, когда это происходит, мы игнорируем возникающие комплексные числа.
До сих пор во всех примерах не было триггерных функций, экспоненциальных функций, и т. д. . в них. Мы не должны ожидать, что так будет всегда. Итак, давайте взглянем на некоторые примеры, в которых используются не только степени \(x\).
Пример 4. Определить все критические точки функции. \[y = 6x — 4\cos \left( {3x} \right)\]
Показать решение
Сначала получите производную и не забудьте применить цепное правило ко второму члену.
\[y’ = 6 + 12\sin\left( {3x} \right)\]
Теперь это будет существовать везде, поэтому не будет критических точек, для которых производная не существует. Единственными критическими точками будут точки, в которых производная равна нулю. Нам нужно будет решить,
Нам нужно будет решить,
\[\begin{align*}6 + 12\sin \left( {3x} \right) & = 0\\ \sin \left( {3x} \right) & = — \frac{1}{2}\ конец {выравнивание *} \]
Решение этого уравнения дает следующее.
\[\begin{align*}3x & = 3,6652 + 2\pi n,\hspace{0,25in}n = 0, \pm 1, \pm 2, \ldots \\ 3x & = 5,7596 + 2\pi n, \hspace{0.25in}n = 0, \pm 1, \pm 2, \ldots \end{align*}\]
Не забудьте \(2 \pi n\) на них! В будущем будут проблемы, в которых мы упустим решения без этого! Также убедитесь, что он надет на этом этапе! Теперь разделите на 3, чтобы получить все критические точки для этой функции.
\[\begin{align*}x &= 1,2217 + \frac{{2\pi n}}{3},\hspace{0.5in}n = 0, \pm 1, \pm 2, \ldots \\ x &= 1,9199 + \frac{{2\pi n}}{3},\hspace{0.5in}n = 0, \pm 1, \pm 2, \ldots \end{align*}\]
Обратите внимание, что в предыдущем примере мы получили бесконечное количество критических точек. 2}}}\]
92}\left( {\frac{3}{{3x}}} \right)\\ & = 2x\ln \left( {3x} \right) + x\\ & = x\left( {2\ln \left( {3x} \right) + 1} \right)\end{align*}\]
2}}}\]
92}\left( {\frac{3}{{3x}}} \right)\\ & = 2x\ln \left( {3x} \right) + x\\ & = x\left( {2\ln \left( {3x} \right) + 1} \right)\end{align*}\]
Теперь этой производной не будет, если \(x\) отрицательное число или если \(x = 0\), но опять же не будет и функции, так что это не критические точки. Помните, что функция будет существовать только в том случае, если \(x > 0\), и достаточно хорошо, что производная также будет существовать только в том случае, если \(x > 0\), поэтому единственное, о чем нам нужно беспокоиться, это где производная равна нулю.
Во-первых, обратите внимание, что, несмотря на внешний вид, производная не будет равна нулю для \(x = 0\). Как отмечалось выше, производная не существует в \(x = 0\) из-за натурального логарифма, и поэтому производная не может быть там равна нулю!
Таким образом, производная будет равна нулю, только если
\[\begin{align*}2\ln \left( {3x} \right) + 1 & = 0\\ \ln \left( {3x} \right) & = — \frac{1}{2}\ конец {выравнивание *} \]
Напомним, что мы можем решить эту задачу, возведя обе части в степень. 92}} \справа)\]
92}} \справа)\]
Эта функция никогда не будет равна нулю ни при каком действительном значении \(x\). Экспонента, конечно, никогда не равна нулю, а многочлен будет равен нулю только в том случае, если \(x\) является комплексным, и помните, что нам нужны только реальные значения \(x\) для критических точек.
Следовательно, у этой функции не будет критических точек.
Важно отметить, что не все функции имеют критические точки! В этом курсе большинство функций, которые мы будем рассматривать, имеют критические точки. Это только потому, что эти проблемы дают более интересные примеры. Не позволяйте этому факту всегда ожидать, что функция будет иметь критические точки. Иногда они этого не делают, как показал этот последний пример.
Калькулятор критических точек с шагами
Онлайн-калькулятор критических точек с шагами поможет вам определить локальные минимумы и максимумы, стационарные и критические точки заданной функции. Этот искатель критических точек различает и применяет правило мощности для определения различных точек. С этим руководством вы узнаете, как находить критические точки функции, используя правило производной и степени, и многое другое!
С этим руководством вы узнаете, как находить критические точки функции, используя правило производной и степени, и многое другое!
Критическая точка — это широкий термин, используемый во многих областях математики. Когда речь идет о функциях действительных переменных, критическая точка — это точка в функциональной области, где функция не дифференцируема. При работе с комплексными переменными критическая точка также является точкой, в которой область определения функции не голоморфна или ее производная равна нулю.
Аналогично, для функции нескольких действительных переменных критическая точка — это критическое значение в пределах своего диапазона (где градиент не определен или равен нулю). Критическая точка многомерной функции — это точка, в которой частная производная первого порядка функции равна нулю. 92 соответствует 2x
Таким образом, результат: 8x
Затем калькулятор критических точек с шагами применяет правило степени: x соответствует 1
Следовательно, x равен: 8
Результат: 8x + 8
Наконец, калькулятор критических чисел находит критические точки, полагая f'(x) = 0
8x + 8 = 0
Локальные минимумы
(x, f(x)) = (−1, − 4. 0)
0)
Локальные максимумы
(x, f(x)) = нет локальных максимумов
Корни: [−1]
Как рассчитать критические точки для двух переменных?Чтобы найти эти точки вручную, вам необходимо следовать этим рекомендациям:
- Сначала запишите данную функцию и возьмите производную от всех заданных переменных.
- Теперь примените степенное правило после дифференцирования.
- Затем находит локальные минимумы и максимумы, подставляя 0 вместо переменных.
Однако вы можете найти эти точки с помощью нашего калькулятора критических точек, выполнив следующие действия: 92 равно нулю.
Теперь применим степенное правило: y переходит в 1
Итак, производная: 8x
Применим степенное правило: y переходит в 1
Следовательно, производная 2y равна: 2
Ответ равно: 8 x + 2
Чтобы найти критические точки, положим f'(x, y) = 0
8x + 8y = 0
8x + 2 = 0
Итак, критические числа функции равны:
Корни: {x:−14, y:14}
Как работает калькулятор критических точек с шагами?Онлайн-калькулятор критических чисел находит критические точки несколькими способами, следуя этим рекомендациям:
Ввод:- Сначала введите любую функцию с одной или несколькими переменными.

- Нажмите кнопку расчета, чтобы просмотреть пошаговые расчеты.
- Калькулятор критических точек с пошаговым отображением критических точек для данной функции.
- Он использует правило производной и степени для определения критических и стационарных точек.
Критические точки — это места, где ∇f или ∇f=0 не существует. Критическая точка — это касательная плоскость точек z = f(x, y), горизонтальна или не существует. Все локальные экстремумы и минимумы являются критическими точками.
- Локальные минимумы в точках (−π2,π2),(π2,−π2),
- Локальные максимумы на (π2,π2),(−π2,−π2),
- Седловая точка в точке (0,0).
Если функция не имеет критической точки, то это означает, что наклон не изменится с положительного на отрицательный и наоборот. Итак, критические точки на графике увеличиваются или уменьшаются, что можно найти путем дифференцирования и подстановки значения x.
Итак, критические точки на графике увеличиваются или уменьшаются, что можно найти путем дифференцирования и подстановки значения x.
Используйте этот онлайн-калькулятор критических точек с шагами, которые позволяют вычислить критические точки как для функций с одной, так и с несколькими переменными. Он использует различные методы для точного определения локальных максимумов и минимумов для данной функции одной переменной.
Ссылка:Из источника Википедии: Критическая точка функции одной переменной, Расположение критических точек, Критические точки неявной кривой, Использование дискриминанта.
Из источника Бриллиант: точка непрерывной функции, задачи оптимизации, дифференцируемая функция f, локальный экстремум, точка перегиба.
Калькулятор средней скорости изменения
Калькулятор средней скорости изменения призван помочь вам понять простую концепцию, скрытую за длинным, немного запутанным названием. Какова скорость изменения? Вообще говоря, он показывает взаимосвязь между двумя факторами. Ищите более точное определение средней скорости изменения ниже. Мы также продемонстрируем и объясним формулу средней скорости изменения с парой примеров того, как ее использовать.
Какова скорость изменения? Вообще говоря, он показывает взаимосвязь между двумя факторами. Ищите более точное определение средней скорости изменения ниже. Мы также продемонстрируем и объясним формулу средней скорости изменения с парой примеров того, как ее использовать.
Предпочитаете смотреть , а не читать? Узнайте все, что вам нужно, за 90 секунд с помощью этого видео , которое мы сделали для вас :
Что такое скорость изменения? – определение средней скорости изменения
Все движется. Изменения неизбежны. Начиная с ускорения вашего велосипеда или автомобиля и заканчивая ростом населения, от кровотока в ваших венах до симбиоза ваших клеток, скорость изменений позволяет нам установить ценность, связанную с этими изменениями.
Средняя скорость изменения — это скорость, которая описывает, как в среднем одно число изменяется по отношению к другому . Если у вас есть функция, это наклон линии, проведенной между двумя точками. Но не путайте его с уклоном. Вы можете использовать среднюю скорость изменения для любой заданной функции, а не только для линейных.
Если у вас есть функция, это наклон линии, проведенной между двумя точками. Но не путайте его с уклоном. Вы можете использовать среднюю скорость изменения для любой заданной функции, а не только для линейных.
Формула средней скорости изменения
На следующем рисунке мы отметили две точки, чтобы помочь вам лучше понять, как найти среднюю скорость изменения.
Формула средней скорости изменения:
A = [f(x₂) - f(x₁)] / [x₂ - x₁]
где:
-
(x₁, f(x₁1))-
(x₁, f(x₁1)) – Координаты первой точки; и -
(x₂, f(x₂))– Координаты второй точки.
Если он положительный, это означает, что одна координата увеличивается при увеличении другой. Например, чем больше вы ездите на велосипеде, тем больше сжигаете калорий.
Равен нулю, когда одна координата меняется, а другая нет. Хорошим примером может быть отказ от подготовки к экзаменам. По мере того, как время начинает истекать, количество вещей, которые нужно изучить, не меняется.

Средняя скорость изменения отрицательна, когда одна координата увеличивается, а другая уменьшается. Допустим, вы собираетесь в отпуск. Чем больше времени вы проводите в пути, тем ближе вы к месту назначения.
Как найти среднюю скорость изменения? - первый пример
Рассчитаем среднюю скорость изменения расстояния (среднюю скорость) поезда, идущего из Парижа в Рим (1420,6 км). На следующем графике вы можете увидеть изменение расстояния с течением времени:
Как видите, скорость не была постоянной. Поезд останавливался два раза, а между остановками ехал значительно медленнее. Но для расчета средней скорости единственные переменные, которые имеют значение, — это изменение расстояния и изменение времени. Итак, если координаты первой точки (0, 0), а координаты второй точки — расстояние между двумя городами и время в пути (1420,6, 12,5), то:
A = (1420,6 - 0) / (12,5 - 0) = 113,648 [км/ч]В среднем поезд шел со скоростью 113,648 км/ч.
 Теперь давайте рассмотрим более математический пример.
Теперь давайте рассмотрим более математический пример.Как найти среднюю скорость изменения? - второй пример
Вам дана функция:
f(x) = x² + 5x - 7Найдите среднюю скорость изменения на интервале [-4, 6].
Найдите значения вашей функции для обеих точек:
f(x₁) = f(-4) = (-4)² + 5 × (-4) - 7 = -11f(x₂) = f(6) = 6² + 5 × 6 - 7 = 59Используйте уравнение средней скорости изменения:
A = [f(x₂) - f(x₁)] / [x₂ - x₁] = [f(6) - f(-4)] / [6 - (-4)] = [59 - (-11) )] / [6 - (-4)] = 70 / 10 = 7
У нас много математических калькуляторов, таких как этот! Если вам понравился калькулятор средней скорости изменения, не стесняйтесь проверить их!
Часто задаваемые вопросы
Является ли средняя скорость изменения такой же, как наклон?
Не совсем . Средняя скорость изменения отражает то, как функция изменяется в среднем между двумя точками .
 С другой стороны, мы определяем наклон функции как наклон линии, касательной к кривой в определенной точке . В линейной функции каждая точка изменяется одинаково, поэтому средняя скорость изменения и наклон равны.
С другой стороны, мы определяем наклон функции как наклон линии, касательной к кривой в определенной точке . В линейной функции каждая точка изменяется одинаково, поэтому средняя скорость изменения и наклон равны.Как найти среднюю скорость изменения функции?
Чтобы найти среднюю скорость изменения функции, выполните следующие действия:
Получить координаты (x, y) начальной точки . Мы назовем их (x₀, y₀).
Получить координаты (x, y) конечной точки . Это будут (x₁, y₁).
Заменить оба в пределах формулы средней скорости изменения (A) :
А = (у₁ - у₀)/(х₁/х₀).
Какова средняя скорость изменения y = 2x?
Средняя скорость изменения y = 2x равна 2 . Поскольку это линейная функция, средняя скорость изменения — это просто наклон функции. В этом случае при каждом изменении координаты x координата y будет удваивать ее.

-

 Первые полторы тысяч разложений.
Первые полторы тысяч разложений.

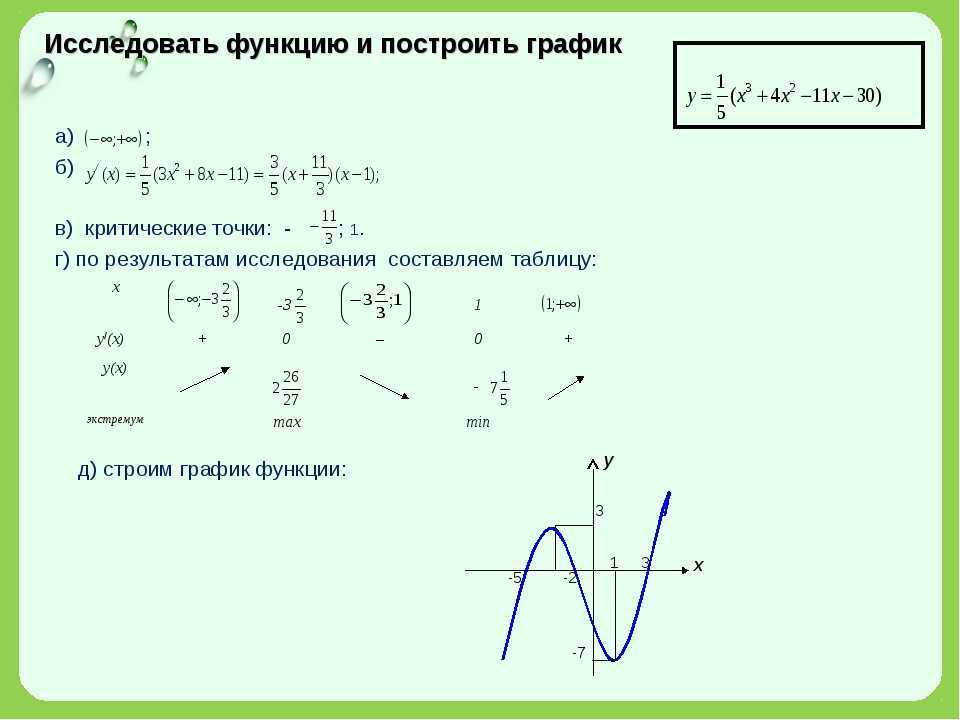 Матрица смежности онлайн
Матрица смежности онлайн