Решение.
Здесь n = 7, х1 = х4 = х6; х2 = х7.
Выборка небольшая. Запишем ее в виде вариационного ряда: –3; –3; –3; –1; 2; 2; 5. Разобьем на интервалы точками –3; –1; 2; 5. Построим статистическую совокупность (с помощью накопленных частот), предварительно записав частоты:
частоты , накопленные частоты: = значит,
Пример 8. По выборке объема 9 найдена эмпирическая функция распределения ДСВ.
Сколько раз в этой выборке наблюдалось возможное значение 8?
Решение.
Объем выборки – n = 9. . Составим статистический ряд, добавив столбец с относительными частотами.
1 | 5 | 3 | |
2 | 8 | 3 | |
3 | 11 | 3 |
1) 2)
3)
Ответ. Возможное значение 8 наблюдалось
3 раза.
Возможное значение 8 наблюдалось
3 раза.
П. 3. Гистограмма и полигон частот
Кроме графика эмпирической функции распределения для наглядного представления выборки бывает полезно построить гистограмму и полигон частот.
Графическим изображением статистического ряда и статистической совокупности (группированного статистического ряда) является гистограмма.
Определение 10. Гистограммой относительных частот статистической совокупности называется кусочно-постоянная функция, постоянная на интервалах совокупности и принимающая на них все значения , где частота, объем выборки, длина интервала, i =1, 2, …, k, k – количество интервалов.
На каждом интервале, как на основании, строится прямоугольник с высотой , площадь которого равна относительной частоте данной группы . Полная площадь ступенчатой фигуры под графиком гистограммы равна 1: .
Замечание. При увеличении объема
выборки и уменьшении интервала группировки
гистограмма относительных частот
является статистическим аналогом
плотности распределения
При увеличении объема
выборки и уменьшении интервала группировки
гистограмма относительных частот
является статистическим аналогом
плотности распределения
Определение 11. Гистограммой частот группированной выборки называется кусочно-постоянная функция, постоянная на интервалах группировки и принимающая на них все значения , где объем выборки, длина интервала, i =1, 2, …, k, k – количество интервалов.
На каждом интервале, как на основании, строится прямоугольник с высотой , площадь которого равна частоте данной группы . Полная площадь ступенчатой фигуры под графиком гистограммы равна объему выборки, т.е. .
Пример 9. Построить гистограмму относительных частот выборки из примера 4.
Решение.
Ко 2-му и 4-му столбцам полученной в
примере 4 таблицы для удобства добавим
столбец со значениями
,
столбцы 1 и 2 удалим.
Границы группы | Относительная частота | |
(–15 ) – (–10) | 0,1 | 0,02 |
(–10) – (–5) | 0,15 | 0,03 |
(–5) – 0 | 0,15 | 0,03 |
0 – 5 | 0,05 | 0,01 |
5 – 10 | 0,05 | 0,01 |
10 – 15 | 0,2 | 0,04 |
15 – 20 | 0,3 | 0,06 |
Пример 10. Построить гистограмму
частот группированной выборки из примера
5.
Построить гистограмму
частот группированной выборки из примера
5.
Гистограмма распределения частот — Энциклопедия по экономике
Вследствие воздействия на производственный процесс случайных факторов возникает вероятность появления отклонений от установленного нормативами номинального значения параметров ЕПК. Для того чтобы определить частоту отклонений и охарактеризовать качество производственного процесса, нужно провести достаточное количество наблюдений и построить гистограмму распределения отклонений по их абсолютному количеству. На рис. 8.2 сплошными линиями показаны примеры гистограмм для двух характерных случаев отклонений. Первый случай. Кроме номинального значения ЕПК устанавливаются допустимые отклонения (допуски). Пример — требования к установке сборных конструкций [c.153]При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах.
 Это необходимо сделать для устранения влияния величины интервала на распределение и получения возможности сравнивать частоты.
[c.32]
Это необходимо сделать для устранения влияния величины интервала на распределение и получения возможности сравнивать частоты.
[c.32]Для достоверной оценки величины и разброса показателей механической торговой системы количество сделок на периоде тестирования не должно быть меньше некоторого минимального значения. Считая, что результат отдельной сделки (например размер прибыли) является случайной величиной, оценим минимальный объем выборки для идентификации закона распределения этой величины. Для идентификации закона распределения необходимо построить гистограмму эмпирических частот и провести сравнение эмпирических и теоретических частот по критерию хи-квадрат. [c.180]
Первичные данные о доходах были трансформированы в ряд распределения, который имеет интервалы шириной 1%, начиная с —8% и заканчивая + 12%. Эти данные будут использованы для составления графиков распределения частот, распределения относительных частот, распределения кумулятивных частот и гистограмм.
 Данные для построения рядов распределения частот приведены в табл. 2.4.
[c.72]
Данные для построения рядов распределения частот приведены в табл. 2.4.
[c.72]Наряду с частотами подсчитываются относительные частоты, накопленные частоты и накопленные относительные частоты. Полученные результаты также записывают в виде таблицы, первая строка которой содержит границы последовательных интервалов, а вторая — соответствующие им частоты (абсолютные, относительные, накопленные и накопленные относительные частоты). Как и для «точечной» выборки, для выборки, сгруппированной по интервалам по значениям накопленных частот, может быть построена выборочная функция распределения. Для наглядного представления выборки часто используют ее графическое отображение — гистограмму частот и гистограмму относительных частот. Любая из этих гистограмм представляет собой кусочно-постоянную функцию, при- [c.257]
Для графического изображения функциональной связи можно воспользоваться системой координат (рис. 12, а). По оси абсцисс откладываются величины значений признака — фонд заработной платы, а по оси ординат — относительные частоты.
Распределение частот. Покажите гистограммы распределения вероятности всех переменных. [c.837]
Гистограмма — это классическое графическое отображение распределения относительных частот появления различных событий в виде колонок (столбиков), которые соответствуют значениям параметров (измеряемых величин) процесса. Такой подход позволяет получить на гистограмме отображения ширины рассеивания и основных моментов распределения (положение, форму). Т. е. появляется возможность сделать закономерности наглядными. Как и карта управления качеством, гистограмма, предназначена в основном для обеспечения качества производственных процессов.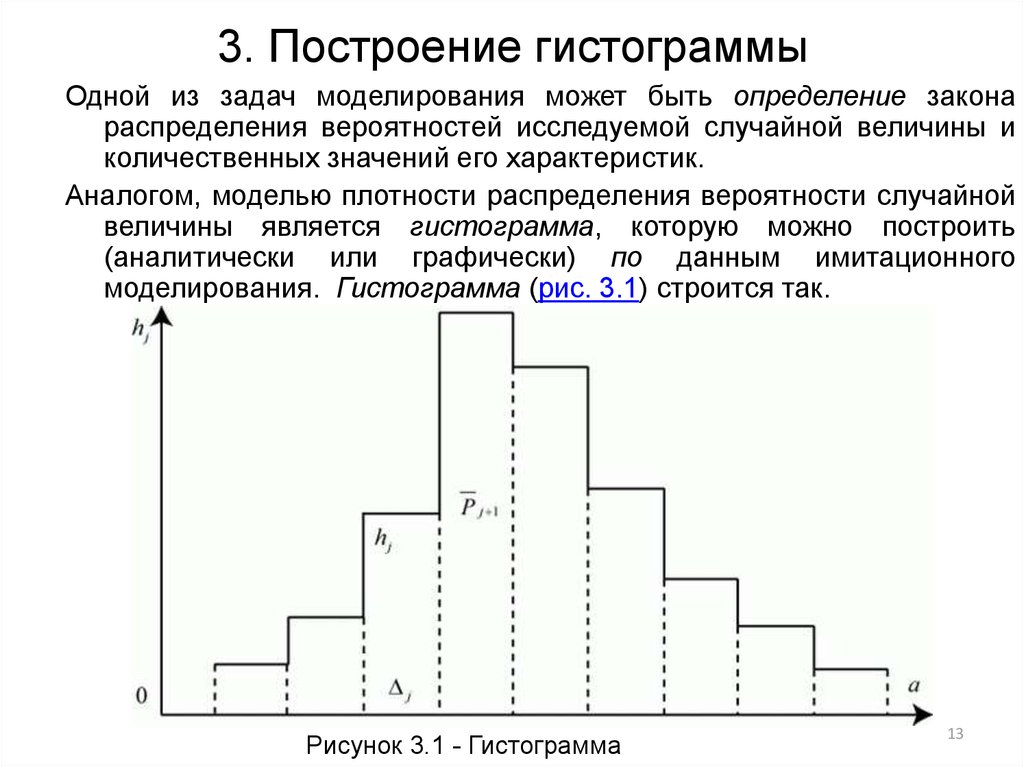
Метод, основанный на вычислении средней арифметической, или просто средней, обычно считается наиболее приемлемым. Он очевиден просто сложите имеющиеся значения и поделите сумму на их количество. Все просто, в том числе отработка данных таблиц частот. Однако, несмотря на всю эту простоту, зачастую этот метод наименее адекватен. Рассмотрим распределение заработной платы на рис. 1.17. Данная диаграмма иллюстрирует типичное распределение доходов всех работников крупной организации. Это положительно асимметричное распределение, с областью больших отклонений в правой части диаграммы. Доходы основной массы работников представлены в левой части диаграммы. Только несколько работников имеют доходы, представленные у верхней границы диаграммы. Вот эти-то несколько работников и искажают значение средней, и усредненное значение, полученное путем расчета арифметической средней, превышает приемлемо репрезентативное значение.
 1.17.
[c.30]
1.17.
[c.30]В установленных пределах определены непересекающиеся интервалы и рассчитаны частоты попадания в них фактических значений времени пролеживания предметов труда. В. табл. 9 приведен интервальный вариационный ряд времени пролеживания на складе детали пакет ротора изделия IV. Предварительные предположения о виде определяемого закона распределения получены на основе анализа гистограммы, которая построена по данному интервальному ряду (рис. 14). Аналогичные исследования интервальных вариационных рядов и гистограмм были проведены для всех рассматриваемых выборочных совокупностей, характеризующих изменения времени пролеживания на межцеховом складе деталей и сборочных единиц в переходящих заделах. [c.75]
Проверка статистических гипотез о виде распределения случайных величин. При построении математической модели исследуемых процессов часто возникают задачи сопоставления полученного материала экспериментов с известными теоретическими распределениями. Если сопоставить вероятность попадания в интервалы, на которые разбита выборка, с соответствующими частотами, полученными из наблюдений, или проводить графическое сравнение полигонов и гистограмм с некоторой теоретической функцией распределения, то можно получить представление о степени близости теоретического и эмпирического распределений.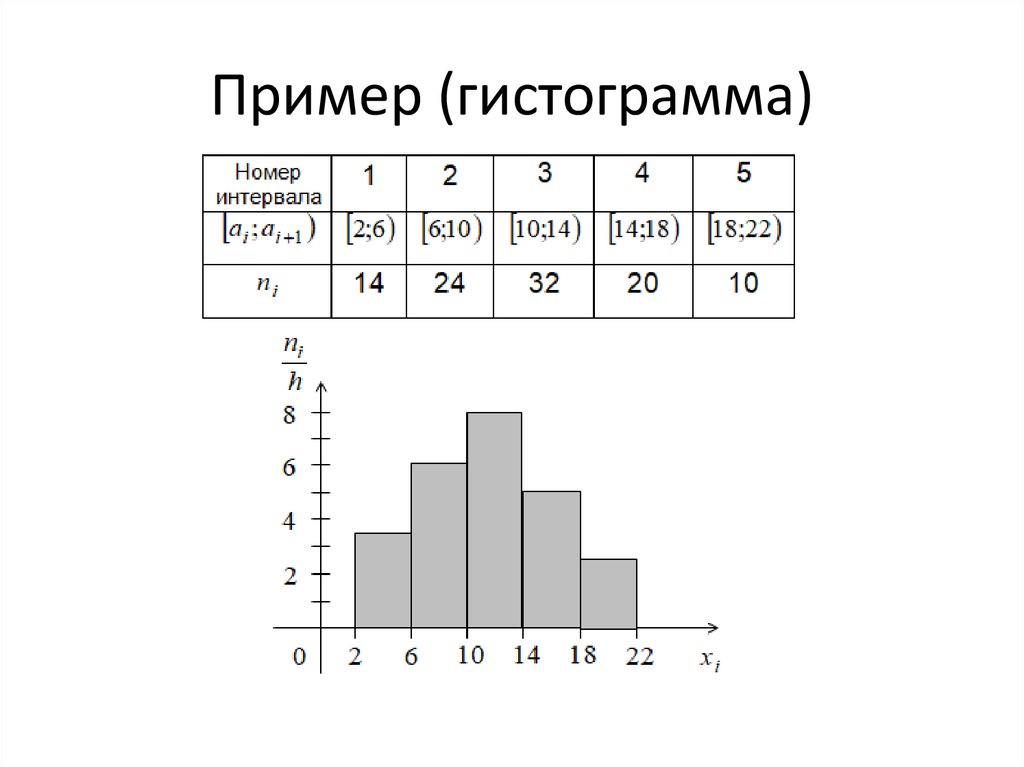 [c.72]
[c.72]
Ниже на рис. 6.3.10 и 6.3.11 приведены гистограмма и полигон распределения относительных частот. [c.314]
Гистограмма должна быть построена так, чтобы площадь каждого «столбика» представляла относительную частоту распределения, а общая их площадь составляла 100% распределения. Горизонтальная ось показывает изменения в доходах на 0,01%. Однако два интервала — «более—0,04 и до 0,02» и «более + 0,02 и до + 0,04» — представляют изменения на 0,02%. [c.74]
Что касается гистограмм, в которых непрерывные данные выражены относительной частотой, то при большом числе данных соответственное сужение интервалов в распределении влечет за собой постепенное приближение гистограммы к гладкой кривой. Если же число данных будет беспредельно большое, то гистограмма превратится в безукоризненную кривую. В этом случае кривая распределения может рассматриваться в качестве распределения генер альной совокупности. [c.56]
Для того чтобы изобразить ряд распределения графически (фиг.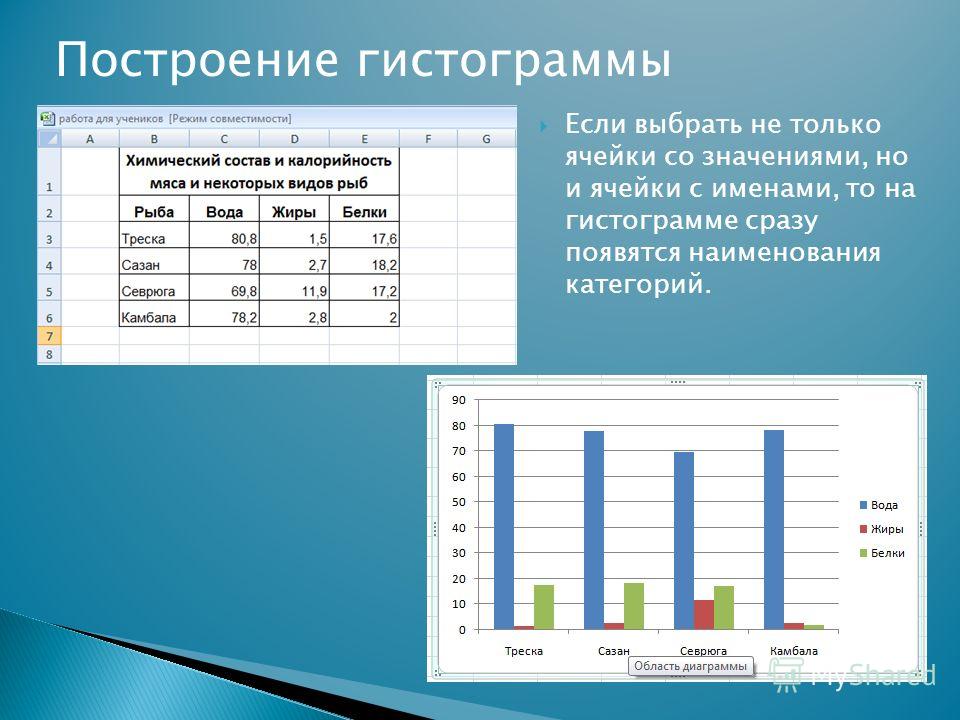 1),по оси X показывают варианты, а по оси К—соответствующие им частоты. Такой график называется гистограммой.
[c.424]
1),по оси X показывают варианты, а по оси К—соответствующие им частоты. Такой график называется гистограммой.
[c.424]
Графическое изображение ряда распределения может быть получено также с помощью полигона. По вертикальной оси этого графика откладывают те же величины, что и при построении гистограммы. По горизонтальной оси откладывают средние точки групп. Таким образом, линейный график, по одной оси которого отложены частоты групп, а по другой — их средние точки, называют полигоном. [c.219]
В отличие от гистограммы столбиковая диаграмма представляет данные по годам, а не группы ряда распределения по горизонтальной оси проставляются годы, а не границы групп ряда распределения по вертикальной оси может быть отложен как результат измерения, так и частота. Прямоугольники не соприкасаются друг с другом и могут иметь любую подходящую, но одинаковую ширину. [c.219]
Гистограммы. Это один из вариантов столбчатой диаграммы, отображающей зависимость частоты попадания значений показателей качества услуги, продукта или процесса в определенный интервал значений.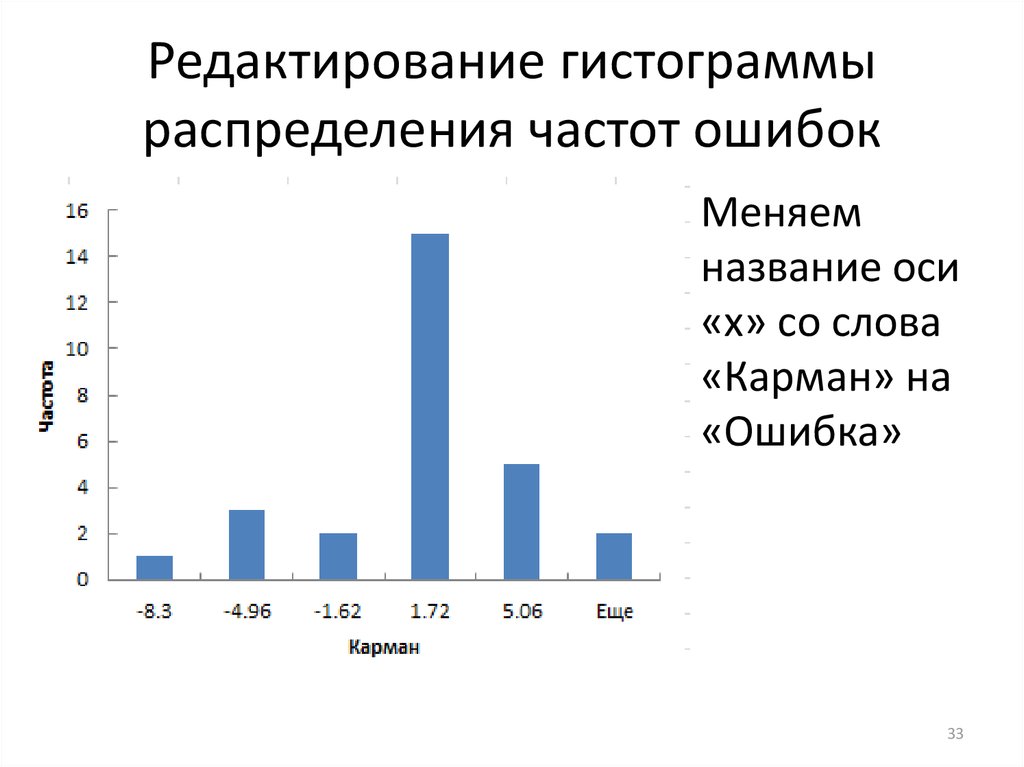 Гистограмма позволяет выявить закон распределения исследуемой величины.
[c.263]
Гистограмма позволяет выявить закон распределения исследуемой величины.
[c.263]
При непрерывной вариации используют, как известно, интервальные вариационные ряды, графическим изображением которых служит гистограмма. Для построения гистограммы по оси абсцисс в соответствии с принятым масштабом откладывают границы интервалов. Эти интервалы являются основаниями прямоугольников, площади которых равны либо пропорциональны частотам или частостям распределения в соответствующих интервалах. [c.57]
Как известно, плотность распределения — это число единиц совокупности, приходящееся на единицу ширины интервала. При равных интервалах плотность распределения прямо пропорциональна частотам или частостям, которые и используются для построения прямоугольников. При неравных интервалах гистограмма строится только по плотности распределения. [c.57]
Обычно не представляется возможным высказать разумную догадку (гипотезу) относительно распределения случайной переменной, пока не будет собрано и проанализировано достаточное количество экспериментальных данных.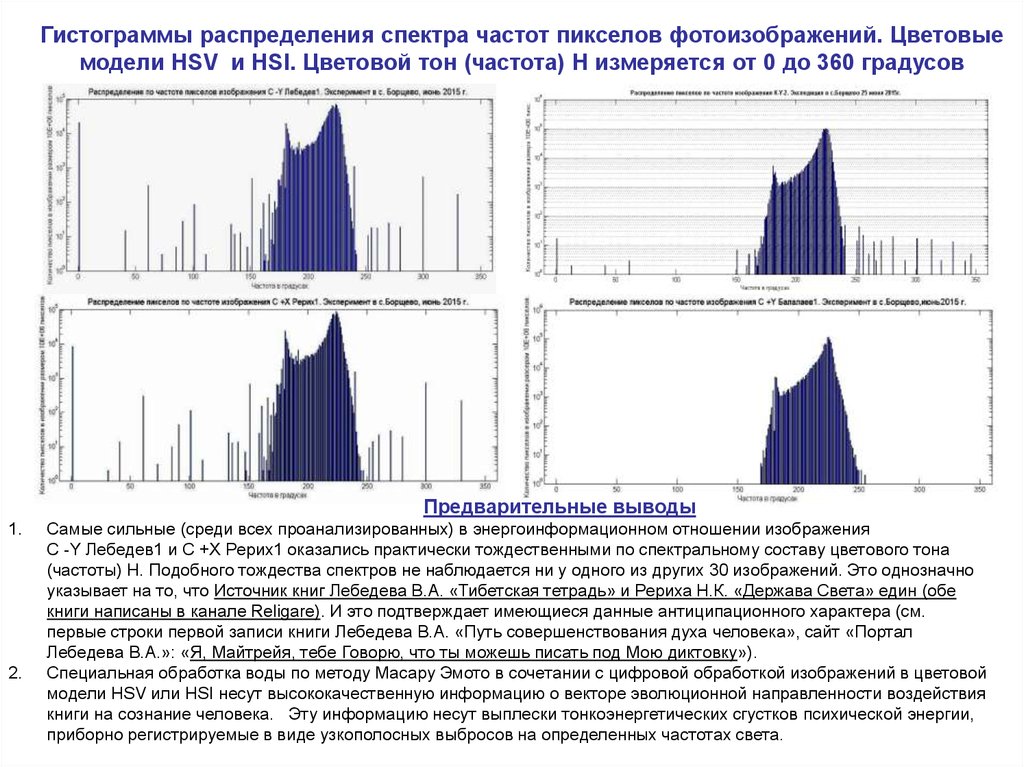 Собранные данные обычно суммируют в виде распределения относительных частот (гистограммы), пример которой приведен на рис.7.3.
[c.90]
Собранные данные обычно суммируют в виде распределения относительных частот (гистограммы), пример которой приведен на рис.7.3.
[c.90]
Если из процесса извлекаются малые выборки фиксированного объема и строится гистограмма распределения числа дефектных изделий, обнаруживаемых в каждой выборке, наблюдается однохвостовое распределение, где большинство выборок содержит нулевой брак, следующая за ней категория — только одно дефектное изделие, следующая-—два дефектных изделия. Если размер распределения значительно возрастает, гистограмма распределения частот числа дефектных изделий в каждой выборке будет несимметричной, но все же будет иметь два хвоста, а вершина распределения — вблизи среднего числа дефектных изделий в выборке. Это распределение частот не описывается нормальным распределением, но, как было установлено, может быть описано биномиальным распределением. [c.129]
Как указывалось (раздел 7.9), гистограмма распределения частот может быть описана распределением Пуассона.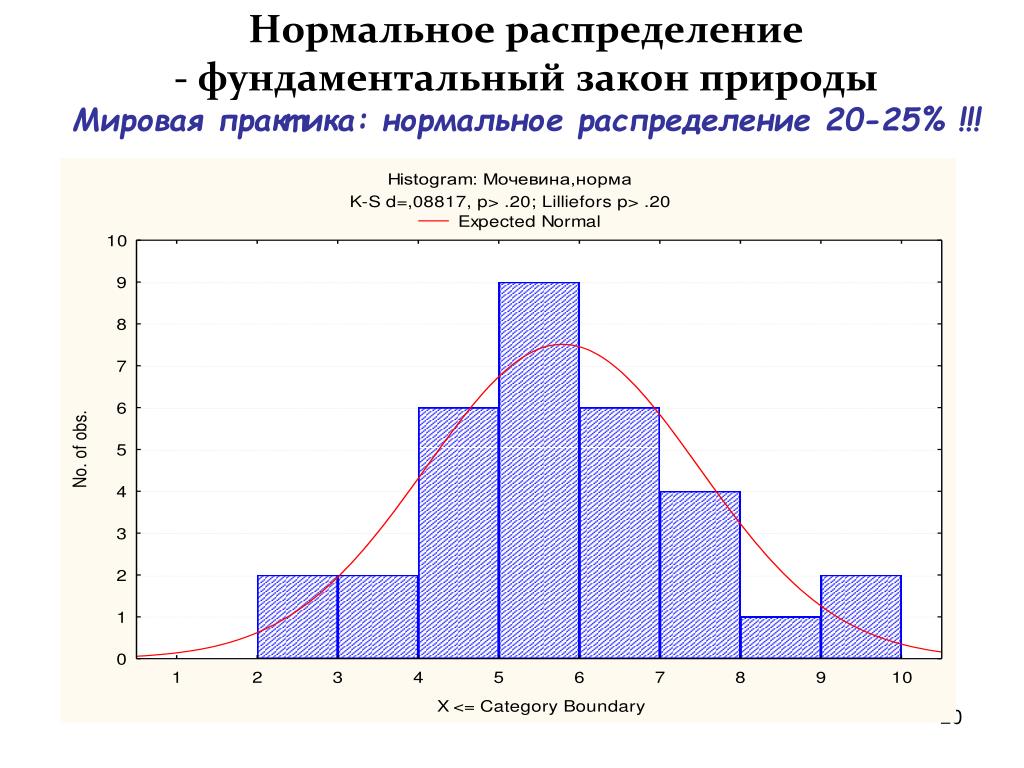 Можно использовать Пуассонову диаграммную бумагу для построения карт, показывающих уровень вероятности, соответствующий пределам корректировки и предупреждения для любой вероятности, а не только для уровней За и 2сг, которые обычно используются. Можно также использовать таблицы для построения пределов корректировки и предупреждения при любых заданных вероятностях.
[c.132]
Можно использовать Пуассонову диаграммную бумагу для построения карт, показывающих уровень вероятности, соответствующий пределам корректировки и предупреждения для любой вероятности, а не только для уровней За и 2сг, которые обычно используются. Можно также использовать таблицы для построения пределов корректировки и предупреждения при любых заданных вероятностях.
[c.132]
Распределение частот количественного признака. Гистограмма и кумулята. Функции распределения вероятностей и плотности распределения вероятности. Типы распределения. Средние величины. Средние степенные квадратические, арифметические, геометрические, гармонические. Мажорантность средних степенных. Средние хронологические. Средние относительные величины. Мода, медиана, квантили. Моменты. Дисперсия, показатель асимметрии, эксцесс, куртозис. [c.49]
Вариационный ряд помогает определить долю неответивших респондентов табл. 15.2 один респондент из 30 не ответил на вопрос), а также указывает долю ошибочных ответов. Значения, равные 0 или 8, соответствуют ошибочным ответам. Следует определить количество случаев с такими значениями и соответственно откорректировать результат. Кроме того, можно установить наличие выбросов, т.е. случаев с экстремальными значениями. При анализе распределения частот относительно размера домохозяйства (семьи) выбросами следует считать несколько семей, состоящих не меньше чем девяти человек. Распределение частот также определяет форму эмпирического распределения значений переменной. Частотные данные можно использовать для построения или вертикальных столбчатых диаграмм, на которых по оси значения переменной, а по оси 7— абсолютные (частоты) или относительные (частости) значения. На рис. представлена гистограмма для данных табл. 15.2. По гистограмме можно проверить, соответствует ли наблюдаемое распределение предполагаемому маркетологом распределению.
[c.557]
Значения, равные 0 или 8, соответствуют ошибочным ответам. Следует определить количество случаев с такими значениями и соответственно откорректировать результат. Кроме того, можно установить наличие выбросов, т.е. случаев с экстремальными значениями. При анализе распределения частот относительно размера домохозяйства (семьи) выбросами следует считать несколько семей, состоящих не меньше чем девяти человек. Распределение частот также определяет форму эмпирического распределения значений переменной. Частотные данные можно использовать для построения или вертикальных столбчатых диаграмм, на которых по оси значения переменной, а по оси 7— абсолютные (частоты) или относительные (частости) значения. На рис. представлена гистограмма для данных табл. 15.2. По гистограмме можно проверить, соответствует ли наблюдаемое распределение предполагаемому маркетологом распределению.
[c.557]
Существенную помощь в анализе вариационного ряда и его свойств оказывает графическое изображение. Интервальный ряд изображается столбиковой диаграммой, в которой основания столбиков, расположенные на оси абсцисс, — это интервалы значений варьирующего признака, а высоты столбиков — частоты, соответствующие масштабу по оси ординат. Графическое изображение распределения хозяйств области по урожайности зерновых культур приведено на рис. 5.l.iДиаграмма этого рода часто называется гистограммой (от греческого слова гистос — ткань, строение).
[c.98]
Графическое изображение распределения хозяйств области по урожайности зерновых культур приведено на рис. 5.l.iДиаграмма этого рода часто называется гистограммой (от греческого слова гистос — ткань, строение).
[c.98]
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| Kataeva_M |
| ||
20/11/20 |
| ||
| |||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Kataeva_M |
| ||
20/11/20 |
| ||
| |||
| Александрович |
| ||
21/01/09 |
| ||
| |||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 5 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Как сделать гистограмму относительной частоты в Excel (3 примера)
Гистограмма относительной частоты — это особый тип диаграммы, который показывает нам скорость возникновения любого события. Этот тип графика также предоставляет нам вероятность этого события. В этом контексте мы продемонстрируем вам, как сделать гистограмму относительной частоты в Excel с тремя простыми примерами . Если вам интересно узнать о процедуре, загрузите нашу рабочую тетрадь и следуйте за нами.
Этот тип графика также предоставляет нам вероятность этого события. В этом контексте мы продемонстрируем вам, как сделать гистограмму относительной частоты в Excel с тремя простыми примерами . Если вам интересно узнать о процедуре, загрузите нашу рабочую тетрадь и следуйте за нами.
Скачать практическую рабочую тетрадь
Что такое относительная частота?
3 подходящих примера для создания гистограммы относительной частоты в Excel
1. Гистограмма относительной частоты для ежедневных данных о доходах отрасли
2. Гистограмма относительной частоты экзаменационных оценок
3. Гистограмма относительной частоты для людей, инфицированных Covid-19.
Вывод
Статьи по Теме
Скачать рабочую тетрадь
Загрузите это учебное пособие для практики, пока вы читаете эту статью.
Что такое относительная частота?
Относительная частота — это специальный тип графика или диаграммы, иллюстрирующий вероятность возникновения какого-либо события.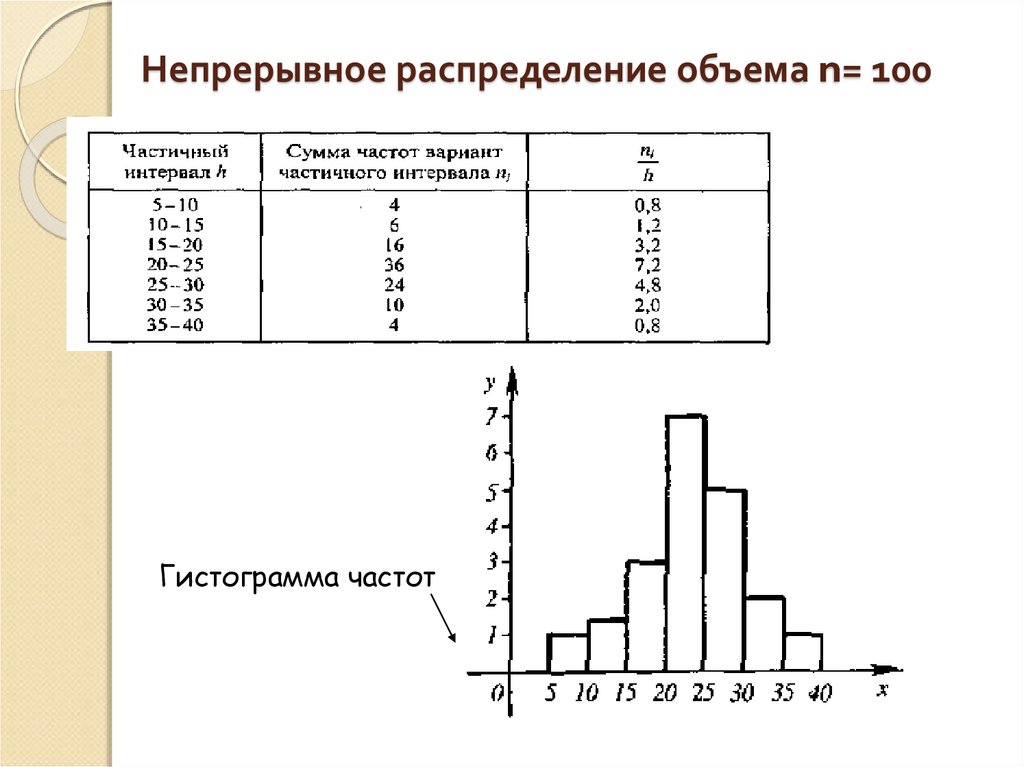 Таким образом, сумма всех относительных частот для любого набора данных будет равна единице. Математическое выражение относительной частоты:
Таким образом, сумма всех относительных частот для любого набора данных будет равна единице. Математическое выражение относительной частоты:
3 подходящих примера для создания гистограммы относительной частоты в Excel
В этой статье мы рассмотрим три простых примера для демонстрации работы по построению гистограммы относительной частоты. Эти примеры набора данных:
- Гистограмма ежедневного дохода отрасли.
- Экзаменационные оценки класса. Гистограмма
- зараженных Covid-19 людей.
1. Гистограмма относительной частоты для данных о ежедневном доходе в отрасли
В этом примере мы рассматриваем набор данных из пяти классов интервалов ежедневного дохода для 75 работников. Интервалы классов (в долларах) находятся в столбце B , а частота (число работников) находится в столбце C .
Шаги для построения гистограммы относительной частоты этого набора данных приведены ниже:
📌 Шаги:
- Прежде всего, вставьте три столбца между интервалами классов и частотой .
 Вы можете добавить столбцы несколькими способами.
Вы можете добавить столбцы несколькими способами. - Затем введите следующие объекты в диапазон ячеек C4:E4 и G4 , как показано на рисунке.
- После этого вручную введите верхний предел ‘51’ и нижний предел ‘100’ в ячейки C5 и D5 соответственно.
- Теперь выберите ячейку E5 и запишите следующую формулу, чтобы получить среднее значение этих двух пределов. Мы используем функцию СРЕДНЕГО для оценки среднего клапана.
=СРЕДНЕЕ(C5:D5)
- Нажмите Введите .
- Аналогичным образом выполните тот же процесс для строки 6 .
- После этого выберите диапазон ячеек B5:E6 и перетащите значок Fill Handle , чтобы скопировать шаблон данных до ячейки E9 .

- Затем мы используем функцию СУММ для суммирования общего количества рабочих. Для этого запишите следующую формулу в ячейку Ф10 .
=СУММ(F5:F9)
- Нажмите клавишу Введите .
- Затем запишите следующую формулу в ячейку G5 , чтобы получить значение относительной частоты . Убедитесь, что вы вводите знак Абсолютная ссылка на ячейку с ячейкой F10 , прежде чем использовать значок Fill Handle .
=F5/$F$10
- Нажмите Введите .
- Дважды щелкните на значке Fill Handle , чтобы скопировать формулу до ячейки G9 .
- Теперь построим гистограмму для значения относительной частоты.

- Для этого выделите диапазон ячеек G5:G9 .
- После этого во вкладке Вставка выберите стрелку раскрывающегося списка из Вставьте столбцы или гистограммы из группы Диаграммы и выберите параметр Clustered Column из раздела 2-D Column .
- Если вы внимательно посмотрите на график, то заметите, что на нашем графике нет значения по оси X.
- Чтобы устранить эту проблему, на вкладке Chart Design щелкните параметр Select Data из группы Data .
- В результате появится диалоговое окно Select Data Source .
- В разделе Метки горизонтальной (категории) оси будет набор случайных чисел 1-5 . Чтобы изменить его, нажмите на опцию Edit .
- Появится еще одно маленькое диалоговое окно под названием Метки осей .
 Теперь выберите диапазон ячеек E5:E9 и нажмите OK .
Теперь выберите диапазон ячеек E5:E9 и нажмите OK .
- Снова нажмите OK , чтобы закрыть диалоговое окно Select Data Source .
- Наконец, вы увидите, что ось X получает среднее значение интервалов нашего класса.
- На этой вкладке также можно изменить дизайн диаграммы. В нашем случае мы выбираем Style 5 из группы Chart Styles .
- Помимо этого, мы сохраняем три элемента диаграммы , которые представляют собой оси , названия осей, и 9.0003 Метки данных . Запишите подходящие названия осей по вашему желанию и выберите положение меток данных на внутреннем конце .
- Все мы знаем, что в гистограмме не будет промежутка между вертикальными столбцами.
- Чтобы устранить это пустое пространство, дважды щелкните на столбцах диаграммы.

- В результате появится боковое окно под названием Окно серии форматов .
- Затем на вкладке «Параметры серии » установите для параметра «Перекрытие серии » значение 0% , а для параметра «Ширина зазора » — значение 0% . Зазор исчезнет.
- После этого, чтобы различить границу столбца, выберите параметр Fill & Line > Border .
- Теперь выберите параметр Сплошная линия и выберите видимый цветовой контраст с цветом столбца.
- Наша гистограмма относительной частоты готова.
Наконец, мы можем сказать, что можем построить гистограмму относительной частоты в Excel.
Подробнее: Как сделать таблицу распределения частот в Excel (4 простых способа)
2. Гистограмма относительной частоты экзаменационных оценок
В следующем примере мы рассматриваем набор данных из семи интервалов экзаменационных оценок для 100 учащихся. Интервалы занятий (баллы) указаны в столбце B , а Частота (количество учащихся) в столбце C .
Интервалы занятий (баллы) указаны в столбце B , а Частота (количество учащихся) в столбце C .
Процедура построения гистограммы относительной частоты этого набора данных выглядит следующим образом:
📌 Шаги:
- Сначала вставьте три столбца между интервалами классов и частотой . Вы можете добавить столбцы несколькими способами.
- После этого введите следующие объекты в диапазон ячеек C4:E4 и G4 , как показано на рисунке.
- Теперь вручную введите верхний предел ‘31’ и нижний предел ‘40’ в ячейки C5 и D5 соответственно.
- После этого выберите ячейку E5 и запишите следующую формулу, чтобы получить среднее значение этих двух пределов.
 Мы используем функция СРЗНАЧ для оценки среднего клапана.
Мы используем функция СРЗНАЧ для оценки среднего клапана.
=СРЕДНЕЕ(C5:D5)
- Затем нажмите Введите .
- Аналогичным образом выполните тот же процесс для строки 6 .
- Затем выберите диапазон ячеек B5:E11 и перетащите значок Fill Handle , чтобы скопировать шаблон данных до ячейки E11 .
- Теперь мы используем функцию СУММ для суммирования общего количества рабочих. Для этого запишите следующую формулу в ячейку F12 .
=СУММ(F5:F11)
- Нажмите клавишу Введите .
- Затем запишите следующую формулу в ячейку G5 , чтобы получить значение относительной частоты.
 Убедитесь, что вы вводите абсолютную ссылку на ячейку 9Подпишите 0004 с ячейкой F12 перед использованием значка Fill Handle .
Убедитесь, что вы вводите абсолютную ссылку на ячейку 9Подпишите 0004 с ячейкой F12 перед использованием значка Fill Handle .
=F5/$F$12
- Аналогично нажмите Введите .
- Дважды щелкните на значке Ручка заполнения , чтобы скопировать формулу до ячейки G11 .
- Теперь построим гистограмму для значения относительной частоты.
- Для этого выделите диапазон ячеек G5:G11 .
- Затем на вкладке Вставить выберите стрелку раскрывающегося списка из Вставить столбцы или гистограммы из группы Диаграммы и выберите параметр Кластеризованный столбец из раздела 2-D столбец .
- Если вы внимательно посмотрите на график, то заметите, что на нашем графике нет значения по оси X.

- Для устранения этой проблемы в Chart Design , нажмите на опцию Select Data из группы Data .
- Появится диалоговое окно Select Data Source .
- В разделе Метки горизонтальной (категории) оси будет набор случайных чисел 1-7 . Чтобы изменить его, нажмите на опцию Edit .
- Появится еще одно маленькое диалоговое окно под названием Axis Labels . Теперь выделите диапазон ячеек E5:E11 и нажмите OK .
- Снова нажмите OK , чтобы закрыть диалоговое окно Select Data Source .
- Наконец, вы увидите, что ось X получает среднее значение интервалов нашего класса.
- На этой вкладке также можно изменить дизайн диаграммы. В нашем случае мы выбираем Style 9 из группы Chart Styles .

- Кроме того, мы сохраняем три элемента диаграммы , которые являются осями , названиями осей, метками данных и . Запишите подходящие названия осей по вашему желанию и выберите положение меток данных на внешнем конце .
- Все мы знаем, что в гистограмме не должно быть пробелов между вертикальными столбцами.
- Чтобы устранить это пустое пространство, дважды щелкните по вертикальным столбцам на диаграмме.
- В результате 9Появится боковое окно 0003 с названием Окно серии форматов .
- После этого на вкладке «Параметры серии » установите для параметра «Перекрытие серии » значение 0% и для параметра «Ширина зазора » значение 0% . Разрыв исчезнет.
- Чтобы различить границу столбца, выберите параметр Заливка и линия > Граница .

- Затем выберите параметр Сплошная линия и выберите видимый цветовой контраст с цветом столбца.
- Наконец, наша гистограмма относительной частоты готова.
Таким образом, можно сказать, что мы можем построить гистограмму относительной частоты в Excel.
Подробнее: Как сделать частотное распределение в Excel (3 простых метода)
3. Гистограмма относительной частоты для людей, инфицированных Covid-19
Теперь попробуем пример другого типа. Мы собираемся рассмотреть набор данных из 10 основных штатов США и количество инфицированных Covid-19. Наш набор данных находится в диапазоне ячеек B5:C14 .
Процесс построения гистограммы относительной частоты этого набора данных приведен ниже:
📌 Шаги:
- Сначала мы используем функцию СУММ для суммирования общего количества рабочих.
 Для этого запишите следующую формулу в ячейку C15 .
Для этого запишите следующую формулу в ячейку C15 .
=СУММ(С5:С14)
- Теперь нажмите Введите .
- После этого запишите следующую формулу в ячейку D5 , чтобы получить значение относительной частоты. Убедитесь, что вы вводите знак Абсолютная ссылка на ячейку с ячейкой C15 , прежде чем использовать значок Fill Handle .
=C5/$C$15
- Аналогично нажмите Введите .
- Затем дважды щелкните на значке Fill Handle , чтобы скопировать формулу до ячейки D14 .
- Теперь построим гистограмму для значения относительной частоты.
- Чтобы построить график, выберите диапазон ячеек D5:D15 .

- После этого на вкладке Вставка выберите стрелку раскрывающегося списка из Вставить столбцы или гистограммы из группы Charts и выберите параметр Clustered Column из раздела 2-D Column .
- Теперь, если вы внимательно посмотрите на график, вы заметите, что на нашем графике нет значения по оси X.
- Чтобы устранить эту проблему, на вкладке Chart Design щелкните параметр Select Data из параметра Data .
- Диалоговое окно под названием Выберите источник данных .
- Затем в разделе Метки горизонтальной (категории) оси будет набор случайных чисел 1-10 . Чтобы изменить его, нажмите на опцию Edit .
- Появится еще одно маленькое диалоговое окно под названием Axis Labels .
 Теперь выберите диапазон ячеек B5:B14 и нажмите OK .
Теперь выберите диапазон ячеек B5:B14 и нажмите OK .
- Снова нажмите OK , чтобы закрыть Диалоговое окно «Выбор источника данных» .
- В итоге вы увидите, что ось X получает названия состояний.
- На этой вкладке также можно изменить дизайн диаграммы. В этом случае мы выбираем Style 4 из группы Chart Styles .
- Кроме того, мы сохраняем три элемента диаграммы , которые представляют собой оси, названия осей, и метки данных . Запишите подходящие названия осей по вашему желанию и выберите позицию Метки данных на внутреннем конце .
- Кроме того, все мы знаем, что в гистограмме не должно быть пробелов между вертикальными столбцами.
- Чтобы удалить это пространство, дважды щелкните по вертикальным столбцам на диаграмме.

- В результате появится боковое окно с названием Окно серии форматов .
- Затем на вкладке «Параметры серии » установите перекрытие серии как 0% и Ширина зазора как 0% . Разрыв исчезнет.
- Чтобы сделать границу столбца видимой, выберите параметр Заливка и линия > Граница .
- Затем выберите параметр Сплошная линия и выберите видимый цветовой контраст с цветом столбца.
- Кроме того, используйте значок изменения размера на краю чата, чтобы получить лучшую визуализацию данных.
- Наконец, наша гистограмма относительной частоты готова.
Итак, мы можем сказать, что можем построить гистограмму относительной частоты в Excel.
Подробнее: Как рассчитать кумулятивную относительную частоту в Excel (4 примера)
Заключение
Вот и конец этой статьи. Надеюсь, что эта статья будет вам полезна и вы сможете построить гистограмму относительной частоты в Excel. Пожалуйста, поделитесь с нами любыми дополнительными вопросами или рекомендациями в разделе комментариев ниже, если у вас есть дополнительные вопросы или рекомендации.
Надеюсь, что эта статья будет вам полезна и вы сможете построить гистограмму относительной частоты в Excel. Пожалуйста, поделитесь с нами любыми дополнительными вопросами или рекомендациями в разделе комментариев ниже, если у вас есть дополнительные вопросы или рекомендации.
Не забудьте посетить наш веб-сайт ExcelDemy , чтобы узнать о некоторых проблемах и решениях, связанных с Excel. Продолжайте изучать новые методы и продолжайте расти!
Связанные статьи
- Расчет стандартного отклонения частотного распределения в Excel
- Найти среднее значение частотного распределения в Excel (4 простых способа)
- Вычисление суммарной частоты в процентах в Excel (6 способов)
- Как сделать категориальную таблицу частот в Excel (3 простых метода)
- Создание сгруппированного частотного распределения в Excel (3 простых способа)
Полное руководство по гистограммам
Что такое гистограмма?
Гистограмма — это диаграмма, отображающая распределение значений числовой переменной в виде ряда столбцов.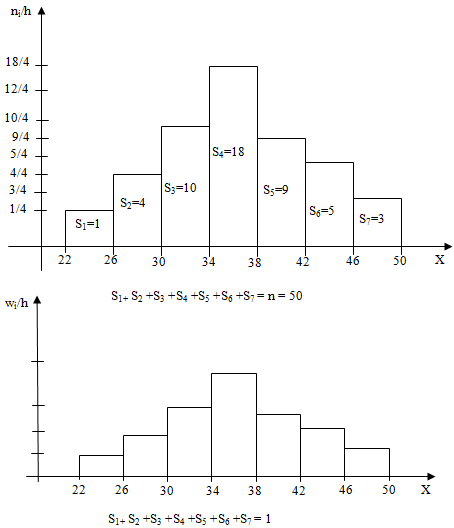 Каждая полоса обычно охватывает диапазон числовых значений, называемый ячейкой или классом; высота столбца указывает частоту точек данных со значением в соответствующем бине.
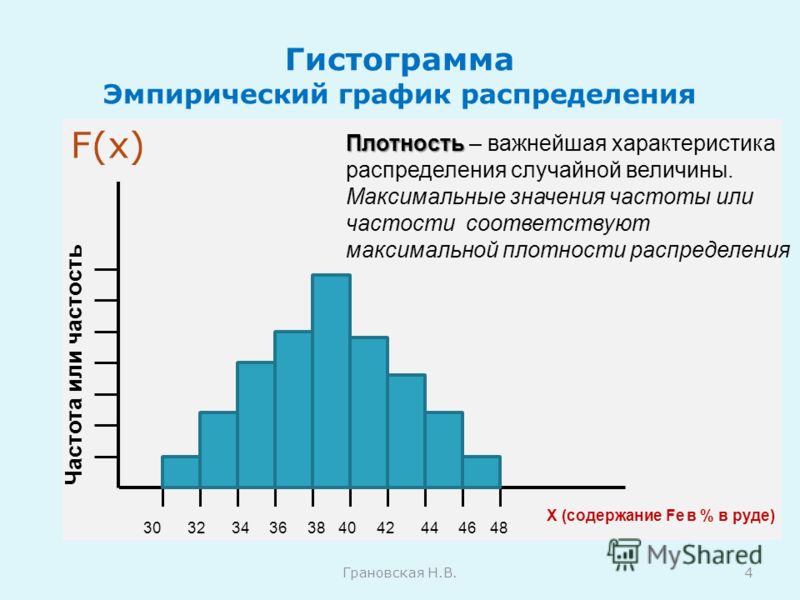
Каждая полоса обычно охватывает диапазон числовых значений, называемый ячейкой или классом; высота столбца указывает частоту точек данных со значением в соответствующем бине.
На приведенной выше гистограмме показано частотное распределение времени ответа на запросы, отправленные в вымышленную систему поддержки. Каждая полоса охватывает один час времени, а высота указывает количество билетов в каждом временном диапазоне. Мы видим, что наибольшая частота ответов была в диапазоне 2-3 часов, с более длинным хвостом справа, чем слева. Есть также холм поменьше, пик (режим) которого находится в диапазоне 13-14 часов. Если бы мы смотрели только на числовую статистику, такую как среднее значение и стандартное отклонение, мы могли бы упустить тот факт, что эти два пика внесли свой вклад в общую статистику.
Когда следует использовать гистограмму
Гистограммы удобны для отображения общих характеристик распределения переменных набора данных. Вы можете примерно увидеть, где находятся пики распределения, является ли распределение асимметричным или симметричным, и есть ли какие-либо выбросы.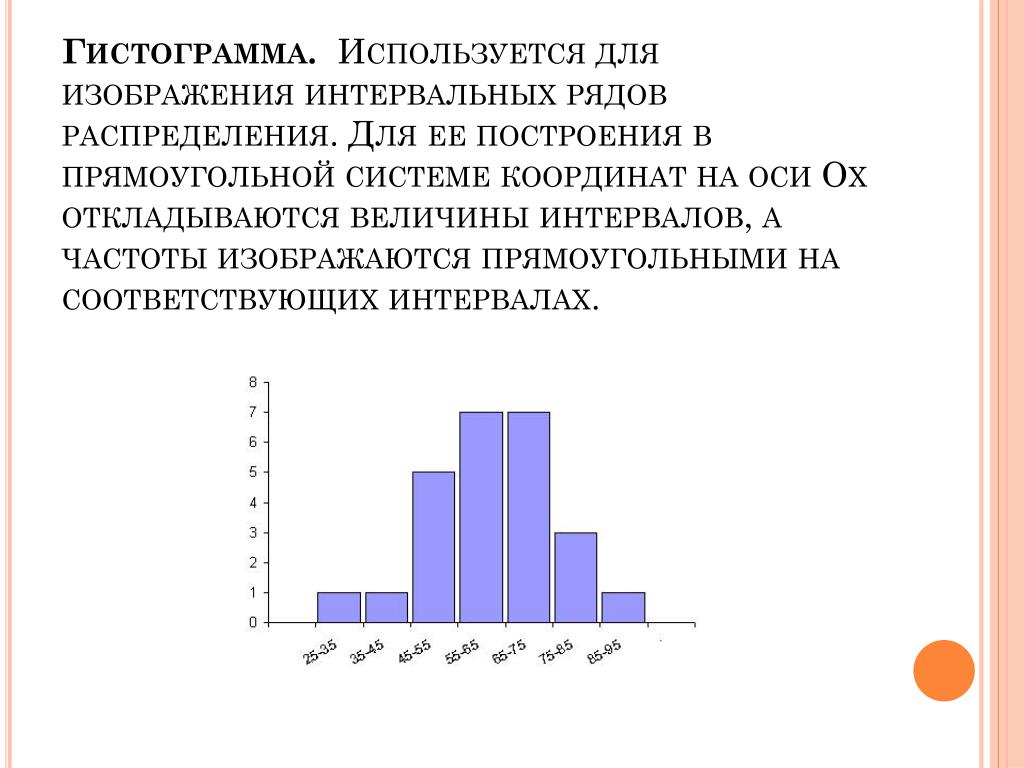
Чтобы использовать гистограмму, нам просто нужна переменная, которая принимает непрерывные числовые значения. Это означает, что различия между значениями постоянны независимо от их абсолютных значений. Например, даже если оценка за тест может принимать только целочисленные значения от 0 до 100, разрыв одинакового размера имеет одинаковое значение независимо от того, где мы находимся на шкале: разница между 60 и 65 равна той же 5-балльной шкале. размер как разница между 9от 0 до 95.
Информация о количестве бинов и их границах для подсчета точек данных не является неотъемлемой частью самих данных. Вместо этого настройка бинов — это отдельное решение, которое мы должны принять при построении гистограммы. То, как мы указываем бины, будет иметь большое влияние на то, как можно интерпретировать гистограмму, как будет видно ниже.
Когда значение находится на границе бина, оно будет последовательно назначено бину справа или слева от него (или в конечные бины, если оно находится в конечных точках).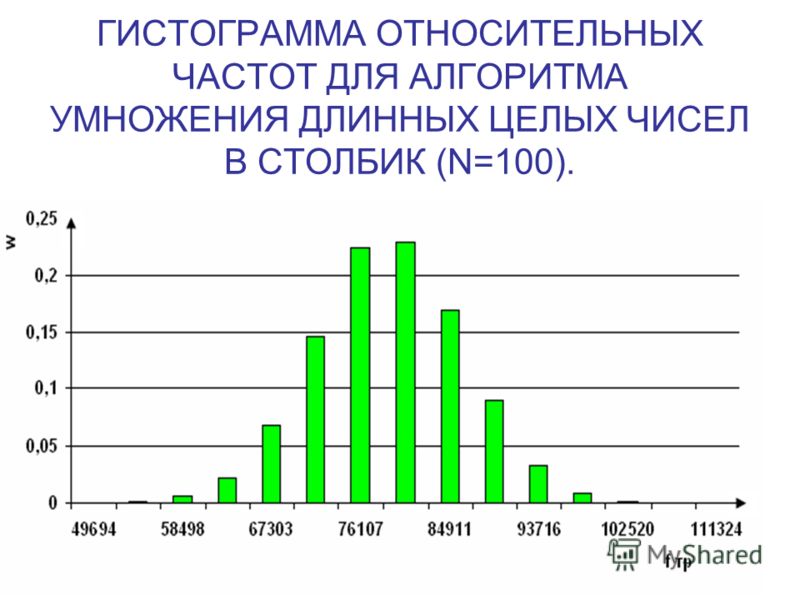 Какая сторона выбрана, зависит от инструмента визуализации; некоторые инструменты имеют возможность переопределить настройки по умолчанию. В этой статье предполагается, что значения на границе бина будут присвоены бину справа.
Какая сторона выбрана, зависит от инструмента визуализации; некоторые инструменты имеют возможность переопределить настройки по умолчанию. В этой статье предполагается, что значения на границе бина будут присвоены бину справа.
Пример структуры данных
Один из способов, которым инструменты визуализации могут работать с данными, которые должны быть визуализированы в виде гистограммы, — это сводная форма, как показано выше. Здесь первый столбец указывает границы бина, а второй — количество наблюдений в каждом бине. Кроме того, некоторые инструменты могут просто работать с исходным столбцом неагрегированных данных, а затем применять указанные параметры бинирования к данным при создании гистограммы.
Рекомендации по использованию гистограммы
Использовать базовую линию с нулевым значением
Важным аспектом гистограмм является то, что они должны быть построены с базовой линией с нулевым значением. Поскольку частота данных в каждом бине определяется высотой каждого столбца, изменение базовой линии или введение пробела в шкале исказят восприятие распределения данных.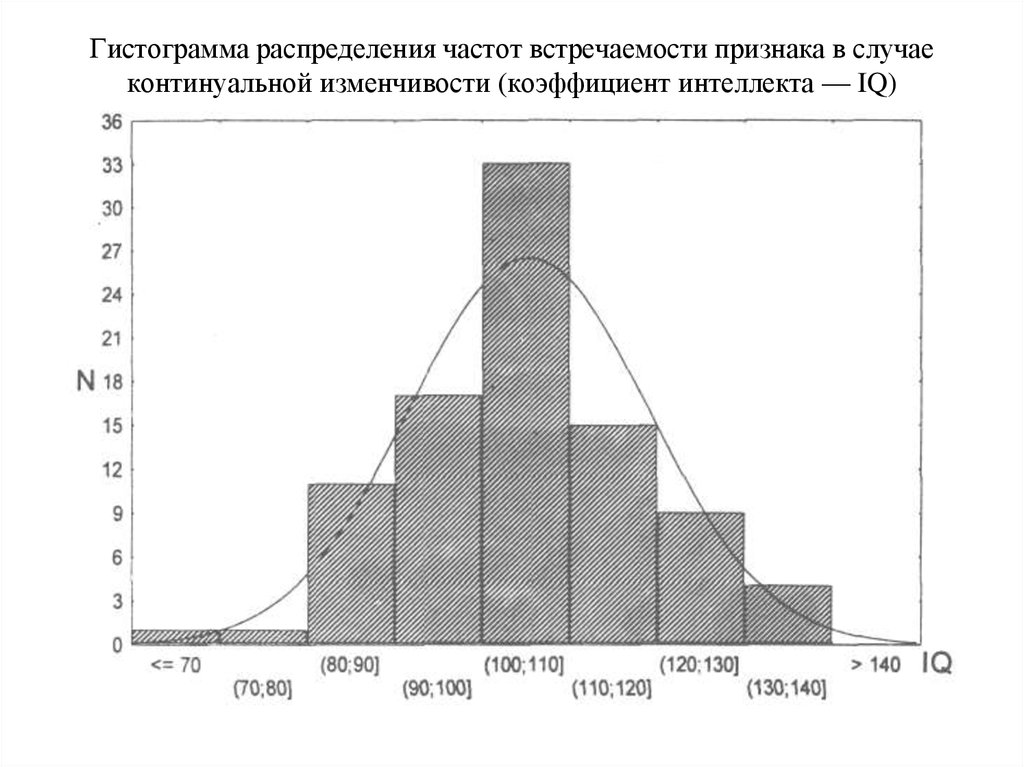
Выберите подходящее количество ячеек
Хотя инструменты, которые могут генерировать гистограммы, обычно имеют некоторые алгоритмы по умолчанию для выбора границ бинов, вы, вероятно, захотите поиграть с параметрами биннинга, чтобы выбрать что-то, что репрезентативно для ваших данных. В Википедии есть обширный раздел, посвященный эмпирическим правилам выбора подходящего количества ячеек и их размеров, но, в конечном счете, стоит использовать знание предметной области, а также изрядно поэкспериментировать с различными вариантами, чтобы узнать, что лучше всего подойдет для ваших целей.
Выбор размера ячейки обратно пропорционален количеству ячеек. Чем больше размеры бинов, тем меньше бинов будет для охвата всего диапазона данных. Чем меньше размер корзины, тем больше корзин должно быть. Стоит потратить некоторое время на то, чтобы протестировать различные размеры бинов, чтобы увидеть, как выглядит распределение в каждом из них, а затем выбрать график, который лучше всего представляет данные.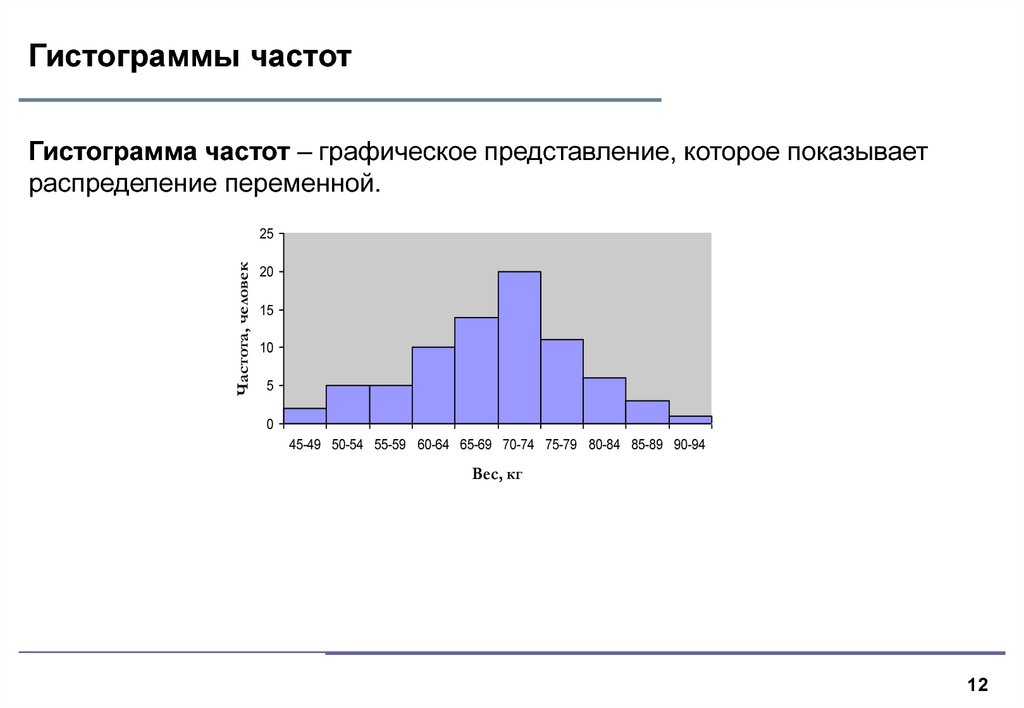 Если у вас слишком много бинов, то распределение данных будет выглядеть грубым, и будет сложно отличить сигнал от шума. С другой стороны, при слишком малом количестве бинов на гистограмме будет не хватать деталей, необходимых для выделения какой-либо полезной закономерности из данных.
Если у вас слишком много бинов, то распределение данных будет выглядеть грубым, и будет сложно отличить сигнал от шума. С другой стороны, при слишком малом количестве бинов на гистограмме будет не хватать деталей, необходимых для выделения какой-либо полезной закономерности из данных.
Выберите интерпретируемые границы бинов
Метки и метки обычно должны располагаться на границах бинов, чтобы наилучшим образом сообщить, где лежат границы каждого столбца. Метки не нужно устанавливать для каждого бара, но наличие их между каждыми несколькими барами помогает читателю отслеживать значение. Кроме того, полезно, если метки представляют собой значения с небольшим количеством значащих цифр, чтобы их было легко читать.
Это говорит о том, что бины размера 1, 2, 2,5, 4 или 5 (которые делят 5, 10 и 20 поровну) или их степени десяти являются хорошими размерами бинов для начала, как эмпирическое правило. Это также означает, что бины размером 3, 7 или 9, вероятно, будет труднее читать, и их не следует использовать, если контекст не имеет для них смысла.
Это также означает, что бины размером 3, 7 или 9, вероятно, будет труднее читать, и их не следует использовать, если контекст не имеет для них смысла.
Небольшое предостережение: убедитесь, что вы учитываете типы значений, которые принимает интересующая вас переменная. В случае дробного размера ячейки, такого как 2,5, это может быть проблемой, если ваша переменная принимает только целые значения. Ячейка от 0 до 2,5 имеет возможность собрать три разных значения (0, 1, 2), но следующая ячейка от 2,5 до 5 может собрать только два разных значения (3, 4 — 5 попадут в следующую ячейку). Это означает, что ваша гистограмма может выглядеть неестественно «ухабистой» просто из-за количества значений, которые может принимать каждый бин.
На рисунке выше показано распределение результатов при суммировании результата пяти бросков кубика, повторенных 20 000 раз. Ожидаемая форма колокола выглядит остроконечной или кривобокой, когда выбираются размеры ячеек, которые охватывают различное количество целочисленных результатов.
Ожидаемая форма колокола выглядит остроконечной или кривобокой, когда выбираются размеры ячеек, которые охватывают различное количество целочисленных результатов.Типичное неправильное использование
Измеряемая переменная не является непрерывной числовой
Как отмечалось во вступительных разделах, гистограмма предназначена для отображения частотного распределения непрерывной числовой переменной. Когда интересующая нас переменная не соответствует этому свойству, вместо этого нам нужно использовать другой тип диаграммы: гистограмму. Переменная, которая принимает категориальные значения, такие как тип пользователя (например, гость, пользователь) или местоположение, явно не является числовой, и поэтому должна использовать гистограмму. Однако существуют определенные типы переменных, которые сложнее классифицировать: те, которые принимают дискретные числовые значения, и те, которые принимают значения, зависящие от времени.
Переменные, принимающие дискретные числовые значения (например, целые числа 1, 2, 3 и т. д.), могут отображаться либо в виде гистограммы, либо в виде гистограммы, в зависимости от контекста. Использование гистограммы будет более вероятным, когда есть много разных значений для построения. Когда диапазон числовых значений велик, тот факт, что значения являются дискретными, как правило, не имеет значения, и хорошей идеей будет непрерывная группировка.
д.), могут отображаться либо в виде гистограммы, либо в виде гистограммы, в зависимости от контекста. Использование гистограммы будет более вероятным, когда есть много разных значений для построения. Когда диапазон числовых значений велик, тот факт, что значения являются дискретными, как правило, не имеет значения, и хорошей идеей будет непрерывная группировка.
Одна важная вещь, на которую следует обращать внимание, это то, что числа представляют реальную стоимость. Если числа на самом деле являются кодами категориальной или неупорядоченной переменной, то это признак того, что следует использовать гистограмму. Например, если у вас есть ответы на опрос по шкале от 1 до 5, кодирующие значения от «полностью не согласен» до «полностью согласен», то частотное распределение следует визуализировать в виде гистограммы. Причина в том, что различия между отдельными значениями могут быть непоследовательными: мы на самом деле не знаем, что значимая разница между 1 и 2 («совершенно не согласен» и «не согласен») такая же, как разница между 2 и 3. («не согласен» на «ни согласен, ни не согласен»).
(«не согласен» на «ни согласен, ни не согласен»).
Более сложный случай, когда интересующая нас переменная является характеристикой, зависящей от времени. Когда значения соответствуют относительным периодам времени (например, 30 секунд, 20 минут), тогда имеет смысл группировать по периодам времени для гистограммы. Однако, когда значения соответствуют абсолютному времени (например, 10 января, 12:15), различие становится размытым. Когда записываются новые точки данных, значения обычно попадают во вновь созданные ячейки, а не в существующий диапазон ячеек. Кроме того, некоторые естественные варианты группирования, например, по месяцам или кварталам, приводят к немного неравным размерам ячеек. По этим причинам нередко можно увидеть другой тип диаграммы, такой как гистограмма или линейная диаграмма.
Использование бинов разного размера
Хотя во всех примерах до сих пор гистограммы демонстрировались с использованием бинов одинакового размера, на самом деле это не является техническим требованием. Когда данных мало, например, когда есть длинный хвост данных, может прийти в голову идея использовать бины большей ширины, чтобы покрыть это пространство. Однако создание гистограммы с бинами разного размера не является ошибкой, но требует значительных изменений в способе создания гистограммы и может вызвать много трудностей при интерпретации.
Когда данных мало, например, когда есть длинный хвост данных, может прийти в голову идея использовать бины большей ширины, чтобы покрыть это пространство. Однако создание гистограммы с бинами разного размера не является ошибкой, но требует значительных изменений в способе создания гистограммы и может вызвать много трудностей при интерпретации.
Техническая особенность гистограмм заключается в том, что общая площадь столбцов представляет собой целое, а площадь, занимаемая каждым столбцом, представляет долю целого, содержащуюся в каждом ячейке. Когда размеры корзин одинаковы, это делает площадь и высоту измеряемой полосы эквивалентными. Однако в гистограмме с переменными размерами ячеек высота больше не может соответствовать общей частоте появления. Это исказило бы представление о том, сколько точек находится в каждом бине, поскольку увеличение размера бина только заставит его выглядеть больше. На центральном графике рисунка ниже ячейки 5-6, 6-7 и 7-10 в конечном итоге выглядят так, как будто они содержат больше точек, чем на самом деле.
. Вместо этого вертикальная ось должна кодировать частоту плотность на единицу размера бина. Например, на правой панели рисунка выше ячейка 2–2,5 имеет высоту около 0,32. Умножьте на ширину бина, 0,5, и мы можем оценить около 16% данных в этом бине. Высота более широких бинов была уменьшена по сравнению с центральной панелью: обратите внимание, как общая форма выглядит похожей на исходную гистограмму с одинаковыми размерами бинов. Плотность — это непростая концепция для понимания, и такой сюжет, представленный другим, незнакомым с этой концепцией, будет трудно его интерпретировать.
Из-за всего этого лучший совет — просто придерживаться абсолютно одинаковых размеров контейнеров. Наличие пустых интервалов и некоторый повышенный уровень шума в диапазонах с разреженными данными, как правило, стоят увеличения интерпретируемости вашей гистограммы. С другой стороны, если есть неотъемлемые аспекты отображаемой переменной, которые предполагают неравные размеры ячеек, то вместо использования гистограммы с неравномерными ячейками вам может быть лучше использовать гистограмму.
С другой стороны, если есть неотъемлемые аспекты отображаемой переменной, которые предполагают неравные размеры ячеек, то вместо использования гистограммы с неравномерными ячейками вам может быть лучше использовать гистограмму.
Общие параметры гистограммы
Абсолютная частота по сравнению с относительной частотой
В зависимости от целей вашей визуализации вы можете изменить единицы измерения на вертикальной оси графика как в терминах абсолютной частоты или относительной частоты. Абсолютная частота — это просто естественное количество вхождений в каждом бине, а относительная частота — это доля вхождений в каждом бине. Выбор единиц оси будет зависеть от того, какие виды сравнений вы хотите выделить в распределении данных.
Преобразуя первый пример в терминах относительной частоты, гораздо проще сложить первые пять тактов, чтобы обнаружить, что примерно на половину заявок отвечают в течение пяти часов.Отображение неизвестных или отсутствующих данных
На самом деле это , а не особенно распространенный вариант, но его стоит учитывать, когда дело доходит до настройки графиков. Если в строке данных отсутствует значение для интересующей нас переменной, оно часто будет пропущено при подсчете для каждого бина. Если важно показать количество пропущенных или неизвестных значений, вы можете объединить гистограмму с дополнительной полосой, отображающей частоту этих неизвестных. При построении этого столбца рекомендуется поместить его на параллельную ось основной гистограммы и другого нейтрального цвета, чтобы точки, собранные на этом столбце, не путались с числовыми значениями.
Если в строке данных отсутствует значение для интересующей нас переменной, оно часто будет пропущено при подсчете для каждого бина. Если важно показать количество пропущенных или неизвестных значений, вы можете объединить гистограмму с дополнительной полосой, отображающей частоту этих неизвестных. При построении этого столбца рекомендуется поместить его на параллельную ось основной гистограммы и другого нейтрального цвета, чтобы точки, собранные на этом столбце, не путались с числовыми значениями.
Гистограмма
Как отмечалось выше, если интересующая переменная не является непрерывной и числовой, а дискретной или категориальной, то вместо нее нам понадобится гистограмма. В отличие от гистограммы, столбцы гистограммы обычно имеют небольшой разрыв между собой: это подчеркивает дискретный характер отображаемой переменной.
Линейная диаграмма
Если вы объединили числовые данные, но хотите, чтобы вертикальная ось вашего графика передала что-то другое, кроме информации о частоте, вам следует рассмотреть возможность использования линейной диаграммы. Вертикальное положение точек на линейной диаграмме может отображать значения или статистические сводки второй переменной. Когда линейная диаграмма используется для изображения частотных распределений, таких как гистограмма, это называется полигон частот .
Вертикальное положение точек на линейной диаграмме может отображать значения или статистические сводки второй переменной. Когда линейная диаграмма используется для изображения частотных распределений, таких как гистограмма, это называется полигон частот .
Кривая плотности
Кривая плотности, или оценка плотности ядра (KDE), является альтернативой гистограмме, которая дает каждой точке данных непрерывный вклад в распределение. На гистограмме вы можете представить себе каждую точку данных как выливание жидкости из ее значения в серию цилиндров ниже (контейнеры). В KDE каждая точка данных добавляет небольшой объем вокруг своего истинного значения, которое складывается по точкам данных для создания окончательной кривой. Форма куска объема — это «ядро», и существует безграничный выбор. Из-за огромного количества опций при выборе ядра и его параметров кривые плотности обычно являются областью программных инструментов визуализации.
Толстые черные штрихи обозначают точки данных, которые влияют на гистограмму (слева) и кривую плотности (справа). Обратите внимание, как каждая точка вносит небольшую кривую в форме колокола в общую форму.
Обратите внимание, как каждая точка вносит небольшую кривую в форме колокола в общую форму.Коробчатая диаграмма и диаграмма для скрипки
Гистограммы хорошо показывают распределение одной переменной, но проводить сравнения между гистограммами довольно сложно, если мы хотим сравнить эту переменную между различными группами. Для двух групп одним из возможных решений является построение гистограмм двух групп вплотную друг к другу. Специфическая для предметной области версия этого типа сюжета — Пирамида населения , которая отображает возрастное распределение мужчин и женщин в стране или другом регионе в виде последовательных вертикальных гистограмм.
Однако, если у нас есть три или более групп, параллельное решение не будет работать. Одним из решений может быть создание многогранных гистограмм, отображающих по одной для каждой группы в строке или столбце. Другой альтернативой является использование другого типа сюжета, например, коробчатого или скрипичного сюжета. Оба эти типа графиков обычно используются, когда мы хотим сравнить распределение числовой переменной по уровням категориальной переменной. По сравнению с гранеными гистограммами эти графики заменяют точное изображение абсолютной частоты более компактным относительным сравнением распределений.
Оба эти типа графиков обычно используются, когда мы хотим сравнить распределение числовой переменной по уровням категориальной переменной. По сравнению с гранеными гистограммами эти графики заменяют точное изображение абсолютной частоты более компактным относительным сравнением распределений.
Инструменты визуализации
Как довольно распространенный тип визуализации, большинство инструментов, способных создавать визуализации, имеют гистограмму в качестве опции. Там, где гистограмма недоступна, гистограмма должна быть доступна в качестве близкой замены. Создание гистограммы может потребовать немного больше работы, чем другие основные типы диаграмм, из-за необходимости протестировать различные варианты группирования, чтобы найти лучший вариант. Однако эти усилия часто того стоят, поскольку хорошая гистограмма может быть очень быстрым способом точно передать общую форму и распределение переменной данных.
Гистограмма — это один из многих типов диаграмм, которые можно использовать для визуализации данных. Узнайте больше из наших статей об основных типах диаграмм, о том, как выбрать тип визуализации данных, или просмотрев полную коллекцию статей в категории диаграмм.
Узнайте больше из наших статей об основных типах диаграмм, о том, как выбрать тип визуализации данных, или просмотрев полную коллекцию статей в категории диаграмм.
Относительные частоты и их распределения
Относительная частота показывает, как часто происходит определенное событие в общем числе наблюдений. Это тип частоты, в котором используются проценты, пропорции и дроби.
В этом посте вы узнаете об относительных частотах, относительном частотном распределении и его кумулятивном аналоге.
Частоты в сравнении с относительными частотами
Частота — это количество определенного события. Например, в этом году Джим прочитал десять книг по статистике. Футбольная команда выиграла 12 игр. Для получения дополнительной информации прочитайте мой пост о частотных таблицах.
Напротив, относительные частоты не используют необработанные подсчеты. Вместо этого они связывают количество событий определенного типа с общим количеством событий, используя проценты, пропорции или дроби. Вот тут-то и появляется термин «родственник» — конкретный подсчет относительно к общему количеству. Например, 25% прочитанных Джимом книг были посвящены статистике. Футбольная команда выиграла 85% игр.
Вот тут-то и появляется термин «родственник» — конкретный подсчет относительно к общему количеству. Например, 25% прочитанных Джимом книг были посвящены статистике. Футбольная команда выиграла 85% игр.
Если вы видите количество, это частота. Если вы видите процент, пропорцию, отношение или дробь, это относительная частота.
Относительные частоты помогают поместить тип события в более широкий контекст. Например, опрос показывает, что 20 студентам больше всего нравится их курс статистики. Из этого необработанного подсчета вы не знаете, большая это пропорция или маленькая. Однако, если бы вы знали, что 30 из 40 (75%) респондентов указали, что им больше всего нравится статистика, вы бы сочли это большим числом!
Кроме того, они позволяют сравнивать значения между исследованиями. Представьте, что школы разного размера опросили своих учеников и получили разное количество респондентов. Если 30 учащихся указывают, что им больше всего нравится статистика, это может быть высокий процент в одной школе и низкий процент в другой, в зависимости от общего количества ответов.
Относительные частоты облегчают сравнение яблок с яблоками.
Как найти относительную частоту
Чтобы вычислить относительную частоту, вы должны знать обе следующие характеристики:
- Количество событий для категории.
- Общее количество событий.
Расчеты относительной частоты преобразуют количество в проценты путем деления количества событий определенного типа на общее количество наблюдений. Его формула следующая:
Например, представьте, что школа опрашивает 50 учеников и просит их назвать свой любимый курс. Тридцать шесть студентов заявляют, что больше всего им нравится статистика.
- Частота ответов «статистика» 36.
- Всего ответов 50.
Чтобы найти относительную частоту для курса статистики, выполните следующее деление: 36 / 50 = 72%.
Относительные частоты как эмпирические вероятности
Относительные частоты также служат эмпирическими вероятностями. Вероятности определяют вероятность наступления событий. Расчеты вероятностей часто сильно зависят от теории. Однако когда вы наблюдаете относительную частоту события, это эмпирическая вероятность. Другими словами, аналитики рассчитывают их, используя реальные наблюдения, а не теорию.
Расчеты вероятностей часто сильно зависят от теории. Однако когда вы наблюдаете относительную частоту события, это эмпирическая вероятность. Другими словами, аналитики рассчитывают их, используя реальные наблюдения, а не теорию.
Эмпирическая вероятность — это количество событий из общего числа наблюдений.
Связанный пост : Основы вероятности
Распределения относительной частоты: таблицы и графики
Распределение относительной частоты описывает относительную частоту для всех возможных результатов в исследовании. В то время как одно значение относится к одному типу событий, распределение отображает проценты для всех возможных результатов. Аналитики обычно представляют эти распределения с помощью таблиц и гистограмм.
Когда вы оцениваете две категориальные переменные вместе, вы можете использовать относительные частоты в таблице непредвиденных обстоятельств. Узнайте больше о таблицах непредвиденных обстоятельств: определение, примеры и интерпретация.
Давайте воплотим их в жизнь на примере!
Пример таблицы
В приведенной ниже таблице относительного распределения частот показано процентное соотношение учащихся в каждом классе в небольшой школе с 88 учениками.
| 9 класс школы0004 | Количество студентов | Относительная частота |
| 1 | 23 | 26,1% |
| 2 | 20 | 22,7% |
| 3 | 15 | 17,0% |
| 4 | 12 | 13,6% |
| 5 | 10 | 11,4% |
| 6 | 8 | 9,1% |
| Всего | 88 | 100% |
Если бы в таблице были только первые два столбца, класс и количество учащихся, это было бы частотное распределение. Распределение частот описывает количество всех возможных исходов. Это процентная колонка, которая делает распределение относительной частоты. Вы можете увидеть, как связаны два типа дистрибутивов.
Это процентная колонка, которая делает распределение относительной частоты. Вы можете увидеть, как связаны два типа дистрибутивов.
Чтобы создать таблицу распределения относительной частоты, возьмите количество учащихся в строке (один класс) и разделите его на общее количество учащихся. Например, в первом ряду 23 первоклассника — 23 из 88 = 26,1%. Для второклассников это 20 из 88 = 22,7%. Повторите этот процесс для всех строк в таблице.
Поскольку в этих таблицах учитываются все возможные результаты, общий процент должен составлять 100 %, за исключением ошибки округления.
Они удобны, потому что вы мгновенно знаете процент от общей суммы для каждого результата, и вы можете определить тенденции и закономерности. Например, первоклассники сами по себе составляют чуть более четверти (26,1%) всей школы. И наоборот, 6 классников составляют лишь 9,1 % учащихся школы. Существует тенденция к снижению значений по мере повышения уровня успеваемости.
Пример гистограммы
Вы также можете использовать гистограммы для отображения относительных частотных распределений. На приведенном ниже графике представлена та же информация, что и в таблице. Он показывает четкую тенденцию к тому, что в старших классах доля учащихся в общем числе учащихся оказывается меньше.
На приведенном ниже графике представлена та же информация, что и в таблице. Он показывает четкую тенденцию к тому, что в старших классах доля учащихся в общем числе учащихся оказывается меньше.
Связанный пост : Гистограммы: использование, примеры и интерпретация
Кумулятивное распределение относительной частоты
Кумулятивное распределение относительной частоты суммирует прогрессию относительной частоты через все возможные результаты. Создание этого типа распределения влечет за собой добавление еще одного столбца в таблицу и суммирование значений по мере продвижения вниз по строкам для создания промежуточного кумулятивного итога.
Для этого примера вернемся к школьникам. В приведенной ниже таблице кумулятивной относительной частоты добавлен последний столбец.
| Класс школы | Количество студентов | Относительная частота | Суммарная относительная частота |
| 1 | 23 | 26,1% | 26,1% |
| 2 | 20 | 22,7% | 48,8% |
| 3 | 15 | 17,0% | 65,8% |
| 4 | 12 | 13,6% | 79,4% |
| 5 | 10 | 11,4% | 90,8% |
| 6 | 8 | 9,1% | 100% |
| Всего | 88 | 100% |
Чтобы найти кумулятивное значение для каждой строки, просуммируйте относительные частоты по мере продвижения вниз по строкам.

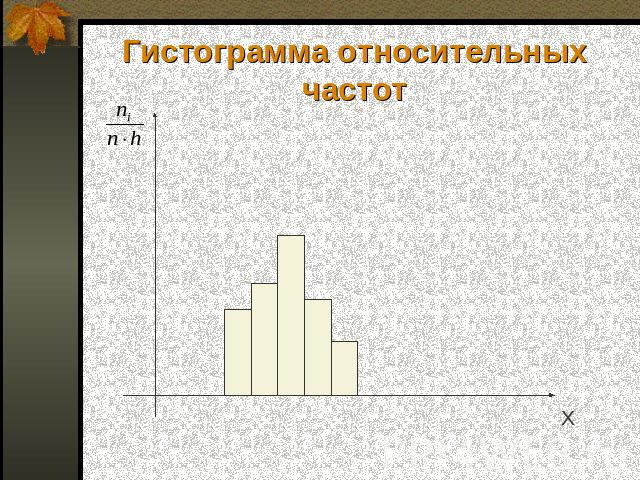 Постройте гистограмму относительных частот.»
Постройте гистограмму относительных частот.»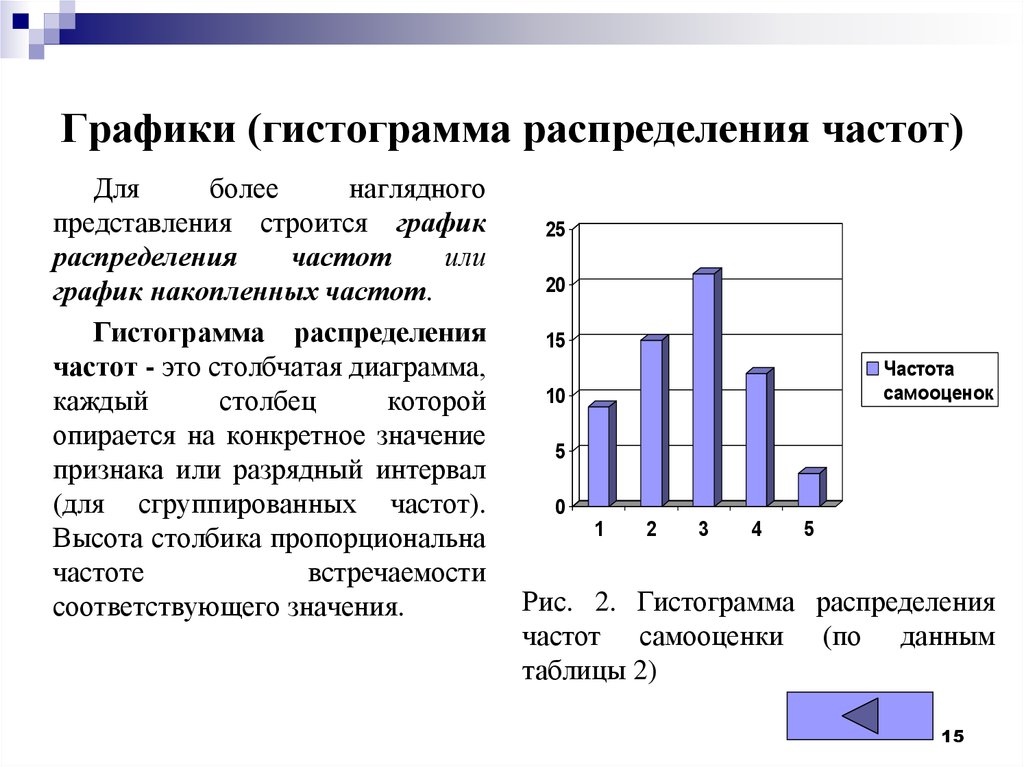
 04.2021, 12:16
04.2021, 12:16 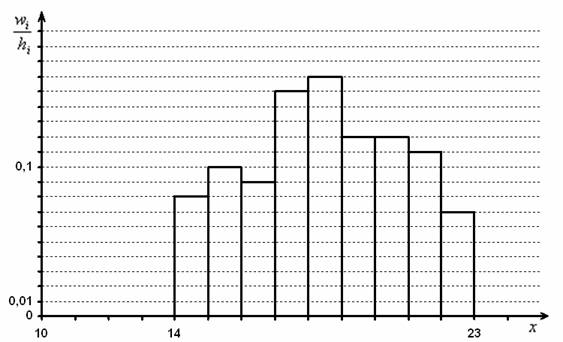 Можно додумать, что интервалы все одинаковые, найти ширину интервалов и восстановить их границы. И построить гистограммы обычным образом.
Можно додумать, что интервалы все одинаковые, найти ширину интервалов и восстановить их границы. И построить гистограммы обычным образом.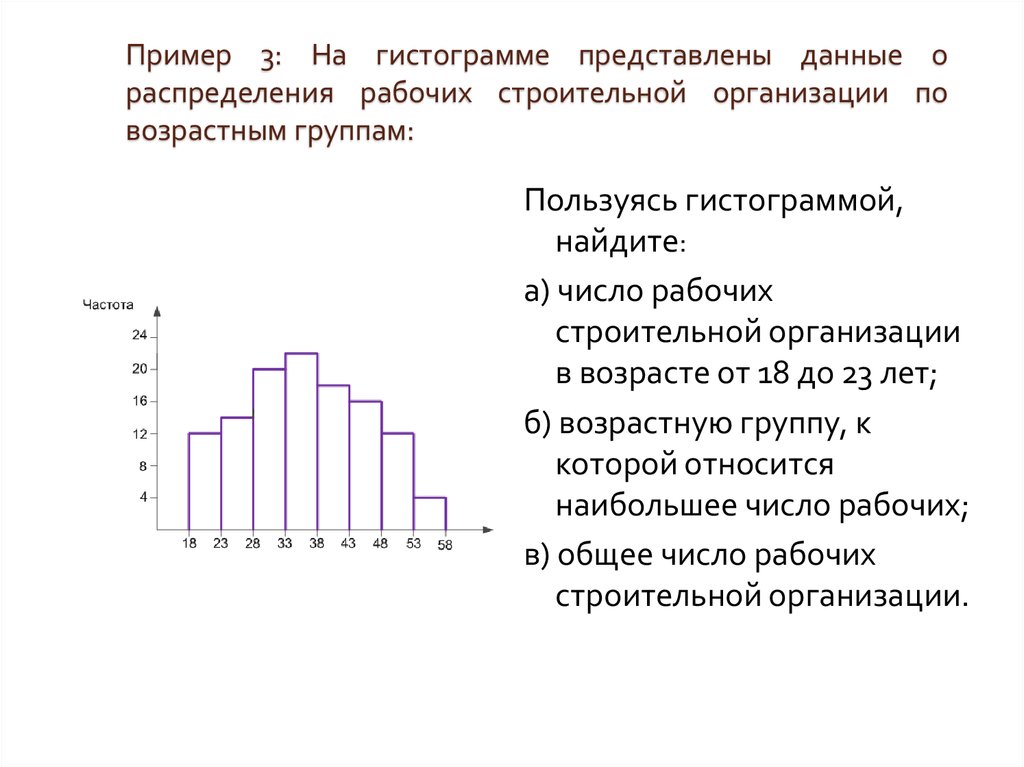
 Что там придумал автор задания — не вем.
Что там придумал автор задания — не вем.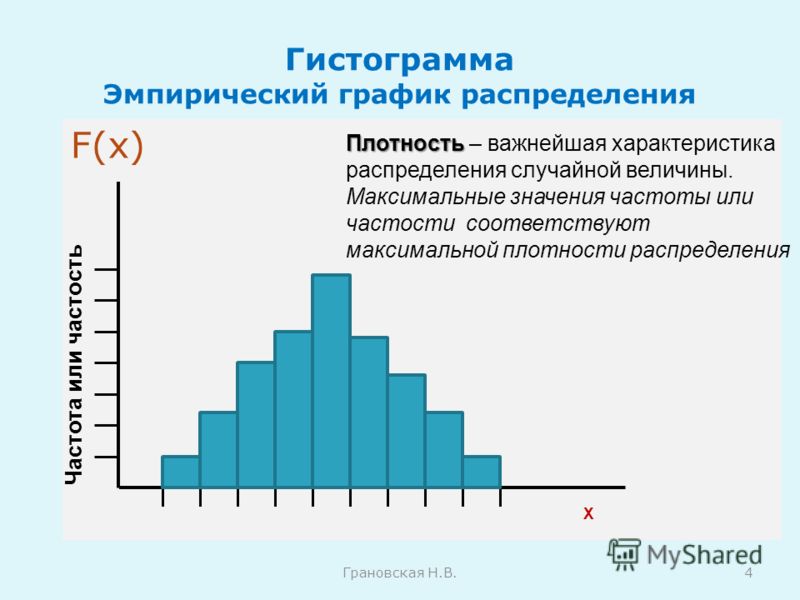 Вы можете добавить столбцы несколькими способами.
Вы можете добавить столбцы несколькими способами.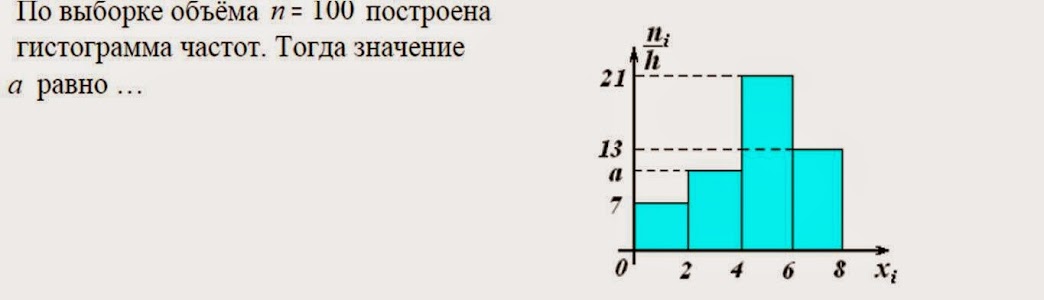
 Теперь выберите диапазон ячеек E5:E9 и нажмите OK .
Теперь выберите диапазон ячеек E5:E9 и нажмите OK .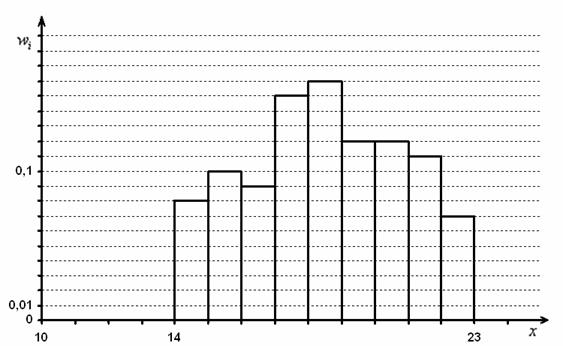
 Мы используем функция СРЗНАЧ для оценки среднего клапана.
Мы используем функция СРЗНАЧ для оценки среднего клапана. Убедитесь, что вы вводите абсолютную ссылку на ячейку 9Подпишите 0004 с ячейкой F12 перед использованием значка Fill Handle .
Убедитесь, что вы вводите абсолютную ссылку на ячейку 9Подпишите 0004 с ячейкой F12 перед использованием значка Fill Handle .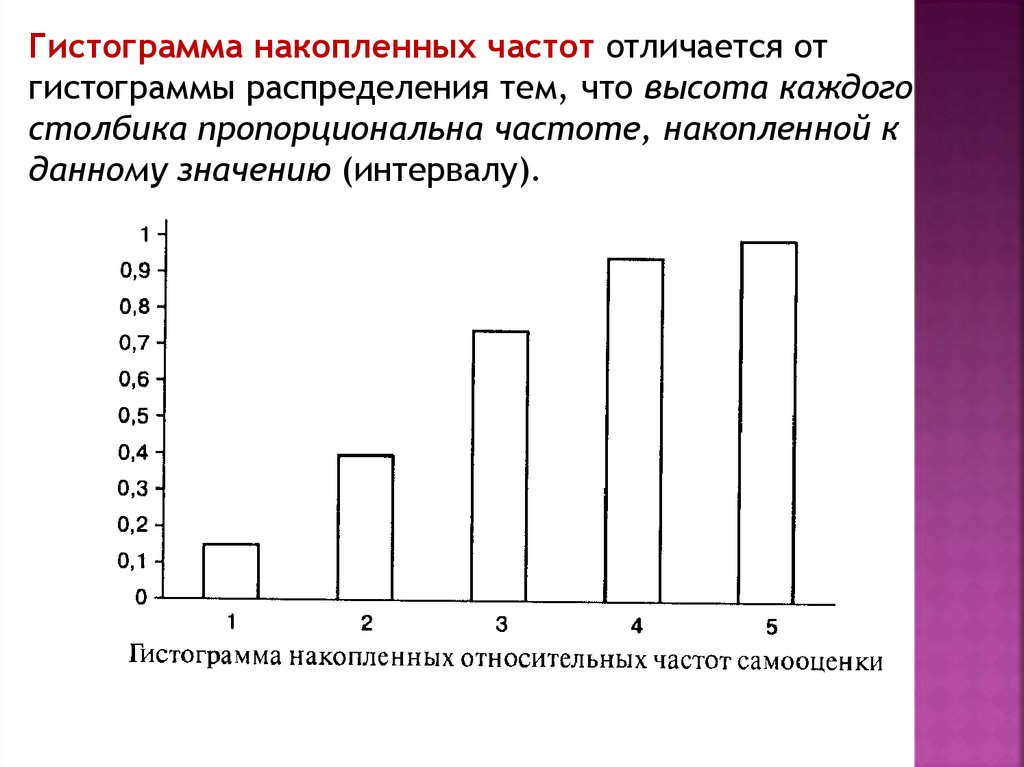

 Для этого запишите следующую формулу в ячейку C15 .
Для этого запишите следующую формулу в ячейку C15 .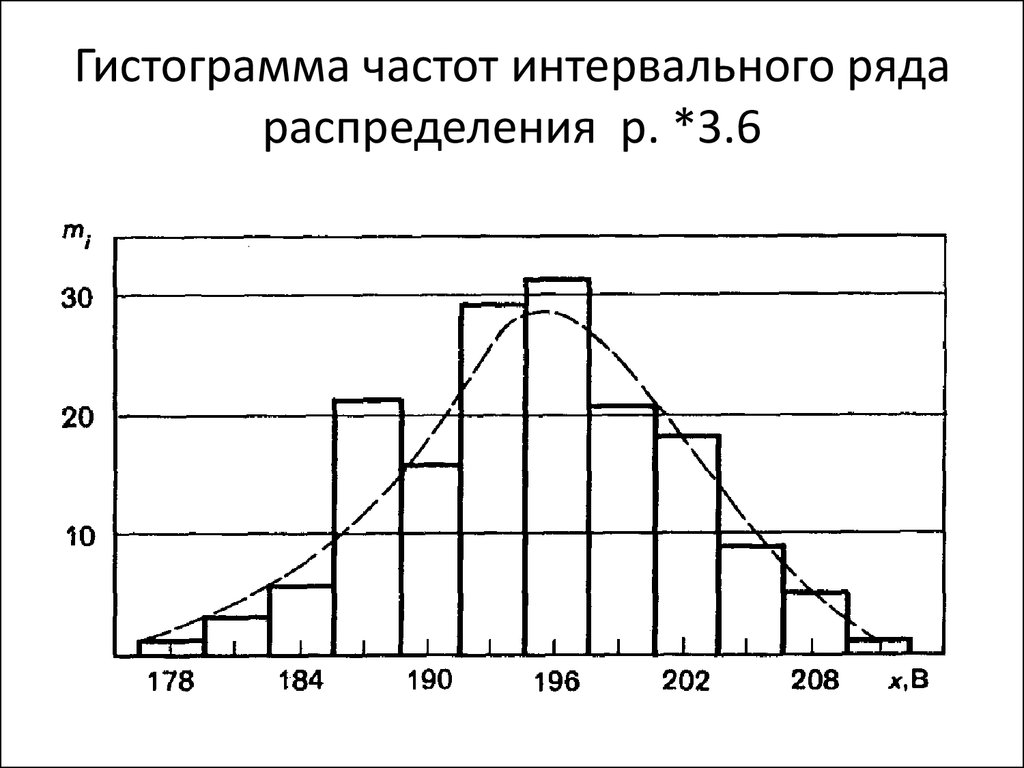
 Теперь выберите диапазон ячеек B5:B14 и нажмите OK .
Теперь выберите диапазон ячеек B5:B14 и нажмите OK .