Найти градиент функции онлайн в точке: Градиент функции онлайн

Производная функции в точке в направлении вектора

Пример №1. Дана функция z=z(x,y), точка A(x₀,y₀) и вектор a. Найти:
1) grad z в точке A; 2) производную данной функции в точке A в направлении вектора a.
z=5x²*y+3xy²

Решение получаем, решая через калькулятор.
Градиентом функции z = f(x,y) называется вектор, координатами которого являются частные производные данной функции, т.е.:

Находим частные производные:


Тогда величина градиента равна:
grad(z)=(10xy+3y²)i+(5x²+6xy)j
Найдем градиент в точке А(1;1): grad(z)A=(10·1·1+3·1²)i+(5·1²+6·1·1)j или grad(z)A=13i+11j
Модуль grad(z):


Направление вектора-градиента задаётся его направляющими косинусами:


Найдем производную в точке А по направлению вектора а(6;-8).

x

Решение.
Градиентом функции z = f(x,y) называется вектор, координатами которого являются частные производные данной функции, т.е.:

Находим частные производные:


Тогда величина градиента равна:

Найдем производную в точке А по направлению вектора а(1;2).

Найти направление вектора — значит найти его направляющие косинусы:

Модуль вектора |a| равен:

тогда направляющие косинусы:

Для вектора a имеем:

Если ∂z/∂a > 0, то заданная функция в направлении вектора a возрастает.
Если ∂z/∂a Пример №4. Дана функция . Найти:
1) gradu в точке A(5; 3; 0);
2) производную в точке А в направлении вектора a=i-2j+k.
Решение.
1. .
Найдем частные производные функции u в точке А.
;;
, .
Тогда
2. Производную по направлению вектора a в точке

А находим по формуле

Частные производные в точке А нами уже найдены. Для того чтобы найти cos α, cos β, cos γ, найдем единичный вектор a₀ вектора a.
, где .

Отсюда

Пример №5. Даны функция z=f(x), точка А(х0, у0) и вектор a. Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора a.
Решение.
Находим частные производные:


Тогда величина градиента равна:

Найдем градиент в точке А(1;1)

или

Модуль grad(z):


Направление вектора-градиента задаётся его направляющими косинусами:


Найдем производную в точке А по направлению вектора а(2;-5).

Найти направление вектора — значит найти его направляющие косинусы:

Модуль вектора |a| равен:

тогда направляющие косинусы:

Для вектора a имеем:

Поскольку ∂z/∂a , то заданная функция в направлении вектора a убывает.

Перейти к онлайн решению своей задачи

3.2. Градиент функции

При изучении скалярных полей наряду с функций рассматривается некоторый вектор, тесно связанный с этой функцией, — градиент скалярного поля.

Градиентом в точке скалярного поля, заданного дифференцируемой функцией , называется вектор, равный

.

Таким образом, каждой точке скалярного поля, заданного дифференцируемой функцией , соответствует не только значение этой функции, но и вполне определенный вектор .

Между градиентом функции в данной точке и производной по направлению в той же точке имеется связь, которая устанавливается следующей теоремой.

Теорема. Проекция вектора На единичный вектор равна производной функции по направлению :

.

Доказательство. Пусть . Из векторной алгебры известно, что проекция какого-либо вектора на другой вектор равна скалярному произведению этих векторов.

Так как , , то

.

Учитывая, что производная по направлению выражает скорость изменения скалярного поля в этом направлении, можно сказать, что проекция на вектор равна скорости изменения поля в направлении вектора .

Обозначим через угол между единичным вектором и . Тогда .

Поэтому .

Если направления векторов и совпадают (), то производная по направлению имеет, очевидно, наибольшее значение, равное .

Таким образом, есть вектор, указывающий Направление наибольшего возрастания

поля в данной точке и имеющий Модуль равный скорости этого возрастания.

Рассмотрим кривую , лежащую на поверхности уровня и проходящую через точку . Градиент функции в точке обладает следующими свойствами: перпендикулярен к вектору , направленному по касательной к кривой в точке .

В случае плоского скалярного поля, заданного дифференцируемой функцией двух переменных , градиент определяется формулой

.

Его связь с производной по направлению выражается равенством

,

Где — угол между единичным вектором и . Вектор перпендикулярен к касательной, проведенной к линии уровня в точке .

Пример 16. Найти наибольшую скорость возрастания функции

в точке .

Решение. Наибольшая скорость возрастания функции равна модулю градиента этой функции. Найдем градиент функции :

,

.

В точке имеем .

Тогда наибольшая скорость возрастания функции равна

.

Пример 17. Найти скорость изменения скалярного поля, определяемого функцией в точке в направлении касательной, проведенной к параболе в этой точке в сторону возрастания координаты , и наибольшую скорость изменения поля в этой точке.

Решение. Скорость изменения скалярного поля в заданном направлении есть производная скалярного поля по направлению вектора , задающего направление.

,

Где ; — направляющие косинусы вектора , . Вектор возьмем на касательной к параболе в , для чего составим уравнение касательной

,

,

— уравнение касательной.

На найденной касательной возьмем точку с любой координатой (), например . Тогда

.

Найдем значения производной по направлению в точке :

,

.

Тогда .

Наибольшая скорость изменения поля в точке есть .

Так как , то

.

Величина наибольшей скорости

.

< Предыдущая		Следующая >

Калькулятор градиента

Чтобы найти градиент, введите многомерную функцию, точки линии и нажмите кнопку рассчитать с помощью калькулятора градиента

РЕКЛАМА

Калькулятор градиента с шагами три точки векторной прямой, взяв частную производную функции. Этот калькулятор предоставляет решение с шагами.

Что такое градиент?

В исчислении градиент — это оператор дифференциала, который применяется к вектор-функции для получения вектора, компоненты которого являются частными производными функции многих переменных по ее переменным.

Градиент похож на склон. Обозначается символом «∇». Применяется к многомерным функциям.

Формула градиента

Формула градиента:

∇ f(x, y, z) = [∂f/∂x ∂f/∂y ∂f/∂z]

Как рассчитать градиент?

Вот несколько решенных примеров градиента, чтобы узнать, как его вычислить.

Пример 1: Для двух точек

Найдите градиент 2x ² – 3y ³ для точек (4, 5).

Решение 

Шаг 1: Запишите данную функцию вместе с обозначением градиента.

∇ f(x, y) = ∇ (2x ² – 3y ³ )

Шаг 2: Теперь возьмите формулу градиента и решите приведенную выше функцию.

∇ f(x, y) = [∂f/∂x, ∂f/∂y]

∇ (2x ² – 3y ³ ) = [∂(2x ²

4 – 3y 34 90 )/∂x, ∂(2x ² – 3y ³ ) /∂y]

∇ (2x ² – 3y ³ ) = [(4x ^{3-4 – 900), (0x 3-4 – 900), – 9y 3-1 )]}

∇ (2x ² – 3y ³ ) = [4x, – 9y ² ]

Теперь замените данные 900 точками.

∇ (2x ² – 3 года ³ ) | _{(x, y)} = [4x, – 9y ² ]

∇ (2x ² – 3y ³ ) | _{(x, y) = (4, 5)} = [4(4), – 9(5) ² ]

∇ (2x ² – 3y ³ ) | _{(x, y) = (4, 5)} = [16, – 9(25)]

∇ (2x ² – 3y ³ ) | _{(x, y) = (4, 5)} = [16, – 225]

Пример 2: Для трех точек

Найдите градиент 3x ³ + 4y ² + 3z 3

34 для точек (2, 3, 4).

Решение 

Шаг 1: Запишите данную функцию вместе с обозначением градиента.

∇ f(x, y, z) = ∇ (3x ³ + 4y ² + 3z ³ )

Шаг 2: Теперь возьмите формулу градиента и решите приведенную выше функцию.

∇ f(x, y, z) = [∂f/∂x, ∂f/∂y, ∂f/∂z]

∇ (3x ³ + 4y ² + 3z ^{3 3 3 3) = [∂(3x 3 + 4y 2 + 3z 3 )/∂x, ∂(3x 3 + 4y 2 + 3z 3 ) /∂y, ∂(3x 3 + 4y 2 + 3z 3 ) /∂z]}

∇ (3x ³ + 4y ² + 3z ³ ) = [(9x ^3-1 + 0 + 0), (0 + 8y ^{3-4 + 90 ), (0 + 0 + 9Z 3-1 )]}

∇ (3x ³ + 4y ² + 3Z ³ ) = [9x ² , 8y, 9z ² ]

Шаг 3: Теперь замените заданные точки.

∇ (3x ³ + 4 года ² + 3z ³ ) | _{(x, y, z)} = [9x ² , 8y, 9z ² ]

∇ (3x ³ + 4y ² + 3z ^{3 4) | _{(x, y, z) = (2, 3, 4)} = [9(2) 2 , 8(3), 9(4) 2 ]}

∇ (3x ³ + 4y ² + 3z ³ ) | _{(x, y, z) = (2, 3, 4)} = [9(4), 8(3), 9(16)]

∇ (3x ³ + 4y ² + 3z ³ ) | _{(x, y, z) = (2, 3, 4)} = [36, 24, 144]

РЕКЛАМА

Найти калькулятор уклона + онлайн-решатель с бесплатными шагами

наклон или градиент двумерной линии, соединяющей две точки, от координат точек. Координаты должны быть двумерными (плоскими).

Калькулятор поддерживает декартову систему координат , которая может представлять как комплексные, так и действительные числа. Используйте «i», чтобы изобразить воображаемую часть, если ваши координаты сложные. Кроме того, обратите внимание, что если вы введете такие переменные, как x или y, калькулятор упростит и представит наклон с точки зрения этих переменных.  

Что такое калькулятор поиска уклона?

Калькулятор поиска уклона — это онлайн-инструмент, который находит наклон/градиент линии, соединяющей любые две точки (координаты которых заданы) на двумерной плоскости.

Интерфейс калькулятора состоит из описания работы калькулятора и четырех текстовых полей ввода. Для удобства рассмотрим координаты двух точек:

p1 = (x1, y1)

p2 = (x2, y2) 

Где xk — абсцисса, а yk — ордината k-й координаты. Калькулятор требует значения абсциссы и ординаты для обеих точек отдельно, и текстовые поля помечены соответствующим образом:

1. $\mathbf{y}$ местоположение для второй координаты: Значение y2.
2. $\mathbf{y}$ местоположение первой координаты: Значение y1.
3. $\mathbf{x}$ местоположение второй координаты: Значение x2.
4. $\mathbf{x}$ местоположение первой координаты:   Значение x1.

В вашем случае использования у вас будут такие значения для x1, x2, y1 и y2, что:

\[ x_1,\,  x_2 ,\, y_1,\, y_2 \, \in \, \mathbb{ {C,\, R}} \]

Где $\mathbb{C}$ представляет набор комплексных чисел, а $\mathbb{R}$ представляет набор действительных чисел. Далее, точки должны быть двухмерными: 92}} \]

Как использовать калькулятор поиска уклона?

Вы можете использовать калькулятор Find the Slope Calculator , чтобы найти наклон линии между двумя точками, просто введя значения координат x и y точек. Например, предположим, что у вас есть следующие точки:

p1 = (10, 5) 

p2 = (20, 8)

Затем вы можете использовать калькулятор, чтобы найти наклон линии, соединяющей две точки.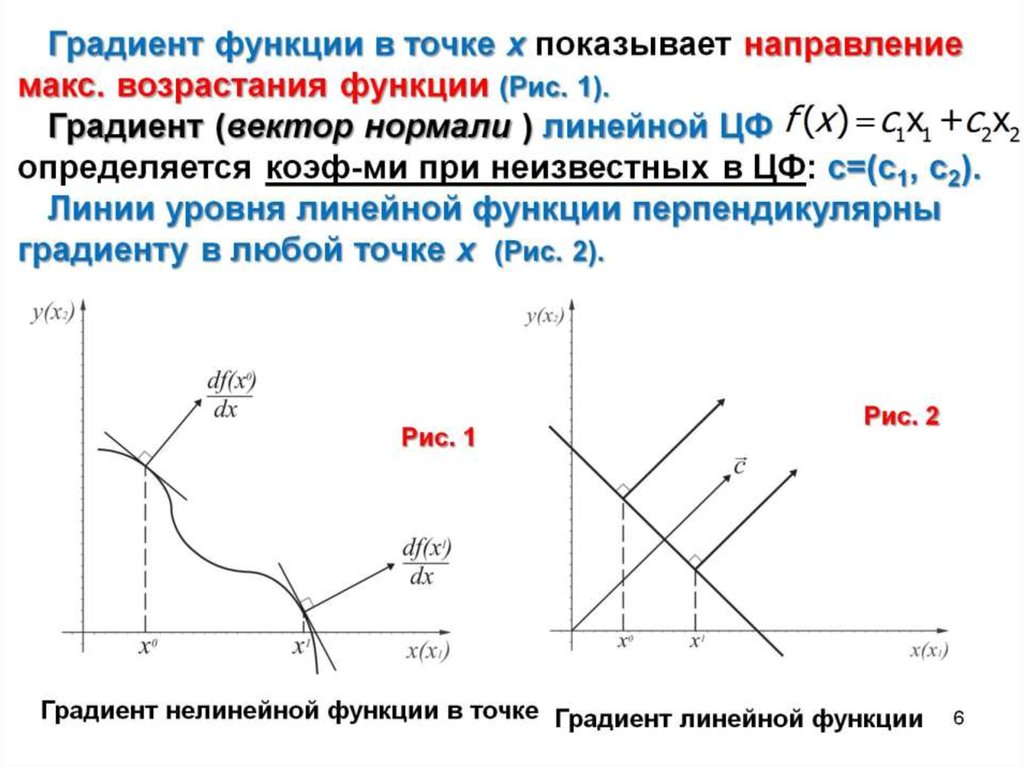 баллов, используя следующие рекомендации:

Шаг 1

Введите значение вертикальной координаты второй точки y2. В приведенном выше примере это 8, поэтому мы вводим «8» без кавычек.

Шаг 2

Введите значение вертикальной координаты первой точки y1. В приведенном выше примере введите «5» без кавычек.

Шаг 3

Введите значение горизонтальной координаты второй точки x2. 20 в примере, поэтому мы вводим «20» без кавычек.

Шаг 4

Введите значение горизонтальной координаты первой точки x1. Например, введите «10» без кавычек.

Шаг 5

Нажмите кнопку Отправить , чтобы получить результаты.

Результаты

Результаты содержат два раздела: «Ввод», , который отображает ввод в форме отношения (формула наклона) для ручной проверки, и «Результат», , который отображает значение самого результата.

В нашем примере калькулятор выводит ввод (8-5)/(20-10) и результат 3/10 $\приблизительно $ 0,3.

Как работает калькулятор поиска уклона?

Калькулятор для поиска уклона работает путем решения следующего уравнения: {\text{run}} = \frac{y_2-y_1}{x_2-x_1} = \frac{\Delta y}{\Delta x} \tag*{$(1)$} \]

Где m равно наклон, (x1, y1) представляет собой координаты первой точки, и (x2, y2) являются координатами второй точки.

Определение

Наклон или градиент 2D-линии, соединяющей две точки или, что то же самое, две точки на линии, представляет собой отношение разности между их координатами y (вертикальная) и x (горизонтальная). Это определение наклона применимо и к линиям.

Иногда определение сокращают до «отношение подъема к пробегу» или просто «подъем к пробегу», где «подъем» — разность по вертикальной координате, а «подъем» — разность по горизонтальная координата. Все эти сокращения находятся в уравнении (1).

Наклон можно использовать для восстановления угла линии, соединяющей две точки. Поскольку угол зависит только от отношения, а наклон включает отношение разницы между координатами y и x, угол равен:

\[ \tan(\theta) = \frac{\Delta y}{\Delta x} = m \]

\[ \theta = \arctan{m} \]

Градиенты линий и кривых

Когда мы говорим о наклоне функции, если это линия, то наклон между любыми двумя точками функции (линии) — это наклон линии между этими двумя точками.

Однако на кривой наклон между любыми двумя точками изменяется с разными интервалами вдоль кривой. Следовательно, наклон кривой, по сути, является оценкой градиента кривой на интервале. Чем меньше этот интервал, тем точнее значение.

Визуально, если интервал на кривой очень мал, линия представляет собой касательную к кривой. Таким образом, в исчислении градиенты или наклоны кривых в различных точках находятся с использованием определения производных . Математически, если f(x) = y, то:

\[ m = \frac{dy}{dx} = \lim_{x \, \to \, 0} \frac{\Delta y}{\Delta x }  \]

Физическое значение и значение уклона

Термин «уклон» буквально означает поднимающуюся или опускающуюся поверхность, один конец которой находится на меньшей высоте, а второй — на большей. Проще говоря, значение уклона относится к крутизне этой наклонной поверхности. Дорога, идущая в гору, является простым примером такой наклонной поверхности.

Понятие наклона встречается в различных разделах математики и физики, особенно в исчислении.

No related posts.