Презентация к уроку геометрии в 9 классе «Синус, косинус, тангенс , котангенс угла» | Презентация к уроку по геометрии (9 класс):
Слайд 1
Синус, косинус, тангенс, котангенс угла. 9 класс Подготовлено учителем математики ГАПОУ СО «БПТ» кадетская(казачья) школа-интернат Коробицыной Е.Л.
Слайд 2
Повторим! А В с С b a
Слайд 3
Задача 1. Найдите тангенс угла B треугольника ABC , изображённого на рисунке. Решение: Ответ. 3,5
Слайд 4
Задача 2. В треугольнике АВС угол А равен 90˚. Найти АВ, если известно, что ВС = 12 см, а А В С Решение: 12 ? = 15(см) Ответ. АВ = 12 см
Слайд 5
Новый материал!
Слайд 6
Определение Полуокружность называется единичной , если ее центр находится в начале координат, а радиус равен 1. M (x; y) C (0; 1) B (-1; 0) A(1; 0) x y O x y D h
Слайд 7
M (x; y) C (0; 1) B (-1; 0) A(1; 0) x y 0 x y D h sin = ∆OMD — прямоугольный MD = y O M = 1 sin = y Синус угла – ордината у точки М cos = OD = x O M = 1 cos = x Косинус угла – абсцисса х точки М Синус, косинус, тангенс угла tg = MD = y = sin OD = x = cos
Слайд 8
M (x; y) C (0; 1) B (-1; 0) A(1; 0) x y 0 x y D h Значения с инуса, косинуса Так как координаты ( х ; у) заключены в промежутках 0 ≤ у ≤ 1, — 1 ≤ х ≤ 1 , то для любого из промежутка 0 ≤ ≤ 180 справедливы неравенства: 0 ≤ sin ≤ 1, — 1≤ cos ≤ 1
Слайд 9
M (x; y) C (0; 1) B (-1; 0) A(1; 0) x y 0 x y D h Значения с инуса, косинуса и тангенса для углов 0 0 , 90 0 и 180 0 0 0 90 0 180 0 sin 0 1 0 cos 1 0 -1 tg 0 — 0 Так как точки А, С и B имеют координаты А (1; 0), С (0; 1), В (-1; 0), то
Слайд 10
M (x; y) C (0; 1) B (-1; 0) A(1; 0) x y 0 x y D h Основное тригонометрическое тождество х 2 + у 2 = 1 — уравнение окружности sin = y , cos = x sin 2 α + cos 2 α = 1 для любого из промежутка 0 ≤ ≤ 180
Слайд 11
Формулы приведения при 0 ≤ ≤ 90 sin (90 — ) = cos cos (90 — ) = sin sin (180 — )= sin cos (180 — ) = — cos при 0 ≤ ≤ 180
Слайд 12
Формулы приведения при 0 ≤ ≤ 90 sin (90 — ) = cos cos (90 — ) = sin C (0; 1) B (-1; 0) A(1; 0) x y 0 D h
Слайд 13
Формулы приведения sin (180 — )= sin cos (180 — ) = — cos при 0 ≤ ≤ 180 C (0; 1) B (-1; 0) A(1; 0) x y 0 D
Слайд 14
Задача 3.
Принадлежат ли единичной окружности точки: М(-1;0), Р , К ? Решение: х 2 + у 2 = 1 — уравнение окружности М(-1;0 ): Р : К : (-1) 2 + 0 2 = 1 1 + 0 = 1 1 = 1 М принадлежит окружности. 2 + 2 = 1 + = 1 1 Р не принадлежит окружности.
Слайд 15
Задача 4. . Найдите Решение: sin 2 α + cos 2 α = 1 cos 2 α = 1 — sin 2 α cos α = cos α = = = =
Слайд 16
Задача 4. . Найдите Решение: sin 2 α + cos 2 α = 1
Слайд 17
Вспомним значения синуса, косинуса и тангенса некоторых углов. 90° 30° x y 0 45° 60° 1 0° 30° 45° 60° 90° 0 1 1 0 tg α 0 1 — ctg α — 1 0 0° 30° 45° 60° 90° 0 1 1 0 tg α 0 1 — ctg α — 1 0
Слайд 18
Задача 5. Решение: sin (180 — )= sin cos (180 — ) = — cos
Слайд 19
Вычисление координат точки 1 М (cos α ; sin α ) x y 0 A cos α sin α
Слайд 20
Задача 6 . Найти координаты точки А, если отрезок ОА = 3, а угол между лучом ОА, пересекающим единичную полуокружность, и положительной полуосью Ох равен 60°. Решение: x y 0 A α = 60° Находим координату х точки А: Находим координату у точки А:
9 класс.
Геометрия. Соотношения между сторонами и углами треугольника. Синус, косинус и тангенс угла. — Синус, косинус и тангенс угла. Основное тригонометрическое тождество.Комментарии преподавателяКак измерить высоту дерева ? Как найти расстояние до недоступной точки , вершины дерева (рис. 1)?
Рис. 1. Наглядный пример из 8 класса о введении тригонометрических функций острого угла
Рис. 2. Прямоугольный треугольник АВС
Пусть задан треугольник (рис. 2), a; – катеты, – гипотенуза, – угол.
Поместим единичную полуокружность в координатную плоскость (рис. 3).
1. Рассмотрим , в нем , где , т. е. это прямоугольный треугольник, угол – острый.
Рис. 3. Единичная окружность в координатной плоскости
Синусом угла называется отношение противолежащего катета гипотенузе :
Но гипотенуза , поэтому:
– ордината точки :
но , значит:
– абсцисса точки единичной полуокружности.
Синус острого угла – это ордината, а косинус – это абсцисса точки первой четверти.
Точка имеет единственную пару координат , – это косинус , – синус .
Но абсциссу и ординату имеют все точки полуокружности.
2. Рассмотрим любой (рисунок 4), из отрезка .
Рис. 4. единичной окружности в координатной плоскости
Его луч определяет единственную точку на полуокружности, ординату назовем синусом , а абсциссу – его косинусом.
примем, что – это отношение к :
Дано:
Найти:
Решение
Рис. 5. Единичная окружность в координатной плоскости
(рис. 5)
По определению, точка с координатами (0;1) есть точка с координатами :
Примечание: т. к. есть 0, то не существует:
Ответ:.
Задача решена.
Дано:
Найти:
Решение
Рис.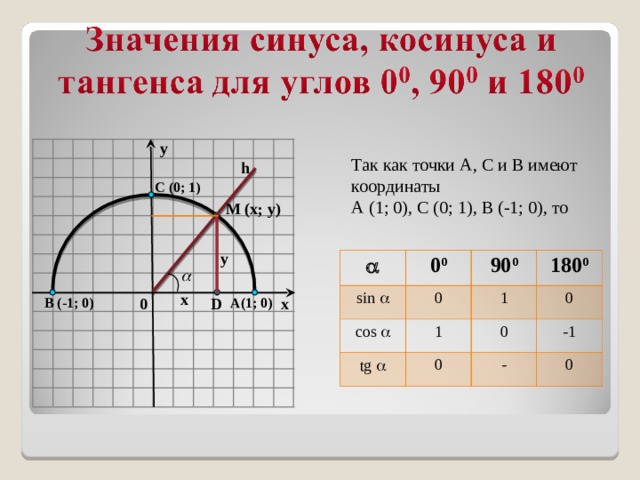
6. Единичная окружность в координатной плоскости
(рис. 6)
Ответ: ; ; .
Задача решена.
Рассмотрим некоторые свойства единичной полуокружности (рис. 7).
Она проецируется на ось в отрезок , а на ось в отрезок , отсюда вывод:
Рис. 7. Единичная полуокружность в координатной плоскости
В частности, косинус тупого угла отрицателен.
Уравнение единичной окружности с центром в точке и :
Для
Именно это соотношение называют основным тригонометрическим тождеством.
Рассмотрим связь тангенса и косинуса.
Если , то из основного тригонометрического тождества имеем:
Такова связь между косинусом и тангенсом.
Пусть .
Тогда из основного тригонометрического тождества найдем связь между котангенсом и синусом:
Проверьте самостоятельно их справедливость с помощью единичной полуокружности.
Вывод
Мы вспомнили, что такое синус, косинус и тангенс для острых углов, узнали, что такое для углов от до , рассмотрели простейшие свойства введённых функций и основные формулы, которые связывают между собой синус, косинус, тангенс и котангенс, причем для всех углов от до .
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/9-klass/sinus-kosinus-i-tangens-ugla/sinus-kosinus-i-tangens-ugla-osnovnoe-trigonometricheskoe-tozhdestvo
http://nsportal.ru/sites/default/files/2015/01/06/sinus_kosinus_i_tangens.pptx
http://dok.opredelim.com/pars_docs/refs/16/15413/img2.jpg
http://5klass.net/datas/algebra/Trigonometricheskie-funktsii/0007-007-Svojstva-sinusa-kosinusa-tangensa-i-kotangensa.jpg
http://math-box.
net/wp-content/plugins/download-form/force_download.php?id=186&token=0b3565eedfb35781a1d4c4e15805a63f
http://www.azdekor.ru/Spektr/SREDN_SKOOL/MATEM/N109/images/geom_9_5.jpg
http://www.cleverstudents.ru/trigonometry/basic_trigonometric_identities.html
http://onlinegdz.net/test-sinus-kosinus-tangens-kotangens-ugla-geometriya-9-klass-atanasyan/
геометрия — Значение синуса, косинуса, тангенса
спросил
Изменено 8 лет, 3 месяца назад
Просмотрено 111 раз
$\begingroup$
Всякий раз, когда у меня возникает вопрос, касающийся синуса, косинуса и тангенса, мой учитель всегда говорит использовать калькулятор. Я хотел бы знать, как бы вы решали их, не используя только калькулятор, чтобы я понимал, что на самом деле делается.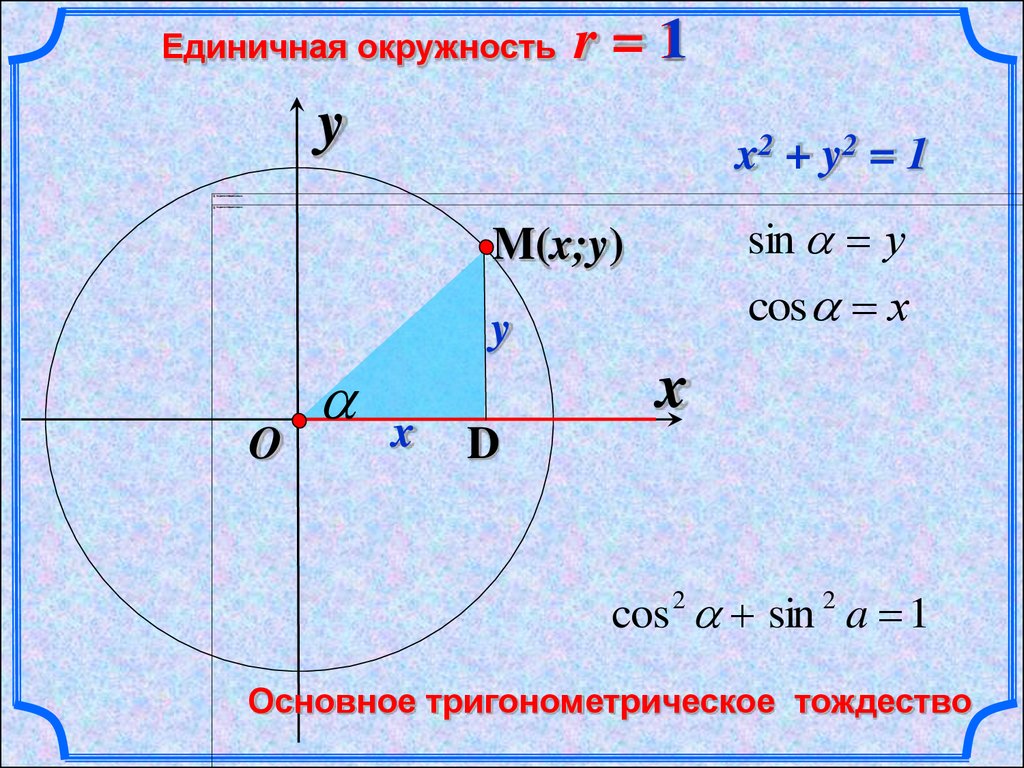
Может ли кто-нибудь объяснить мне, как это сделать и что представляют собой синус, косинус и тангенс?
- геометрия
$\endgroup$
$\begingroup$
$\sin(x)$, $\cos(x)$ и $\tan(x)$ определяются отношениями конкретных сторон прямоугольных треугольников.
$$\sin(A)=\frac{\text{напротив}}{\text{гипотенуза}},\quad\cos(A)=\frac{\text{смежный}}{\text{ гипотенуза}}, \ quad \ tan (A) = \ frac {\ text {напротив}} {\ text {смежно}} $ $ 90)=\frac{1}{\sqrt{2}}$, но с другими нет четкого представления, если вообще есть какое-либо другое представление.
Когда калькулятор выдает строку чисел для $\sin$ угла, он использует определенные алгоритмы, которые были закодированы. Одним из таких алгоритмов является ряд Тейлора. Когда калькуляторы используют эти алгоритмы, они делают это только в радианах (насколько мне известно).
5}{1\cdot2\cdot3\cdot4\cdot5}+\ldots$$
Этот ряд имеет бесконечно много терминов и будет приближаться к значению, чем больше терминов вы используете. Если бы калькулятор выполнял эту серию, он нашел бы первую загрузку терминов, затем остановился и выдал бы то, что нашел (что близко к реальному значению, но является приблизительным). Вы $могли$ сделать это вручную, если бы у вас было много свободного времени или если бы вы были луддитом. Я полагаю, что это будет довольно скучно.
Надеюсь помог!
$\endgroup$
$\begingroup$
Тригонометрические функции — это функции специального вида. Как, например, $2x+4$, за исключением того, что их сложнее вычислить численно.
Определены для всех действительных чисел; определение, с которым вы, вероятно, знакомы (отношения сторон прямоугольных треугольников), используется для их определения для небольших аргументов ($[0;\pi/2]$), которые затем расширяются для других значений.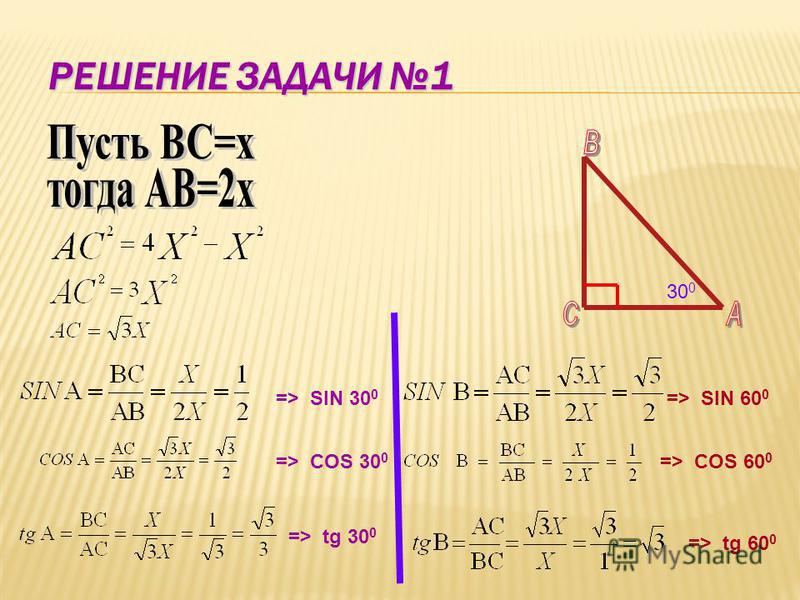
У триггерных функций есть много хороших свойств, а это значит, что они всплывают повсюду в математике, поэтому важно знать, как с ними обращаться.
Насчет того, как их вычислить — ну никак, это сложно. До появления калькуляторов были таблицы, и вы использовали их. Таблицы были составлены вручную очень преданными своему делу людьми с использованием различных формул приближения.
И математика на этом не заканчивается. Специальные функции — это целый класс сложных для вычисления, но важных функций, а триггеры — лишь небольшой их пример.
$\endgroup$
$\begingroup$
До того, как появились калькуляторы (да, я достаточно взрослый, чтобы помнить…), люди использовали логарифмические линейки для грубых вычислений (возможно, три значащих цифры, если повезет) и таблицы триггерных функций для большей точности.
Поверьте мне: вы не хотите использовать ни один из этих методов.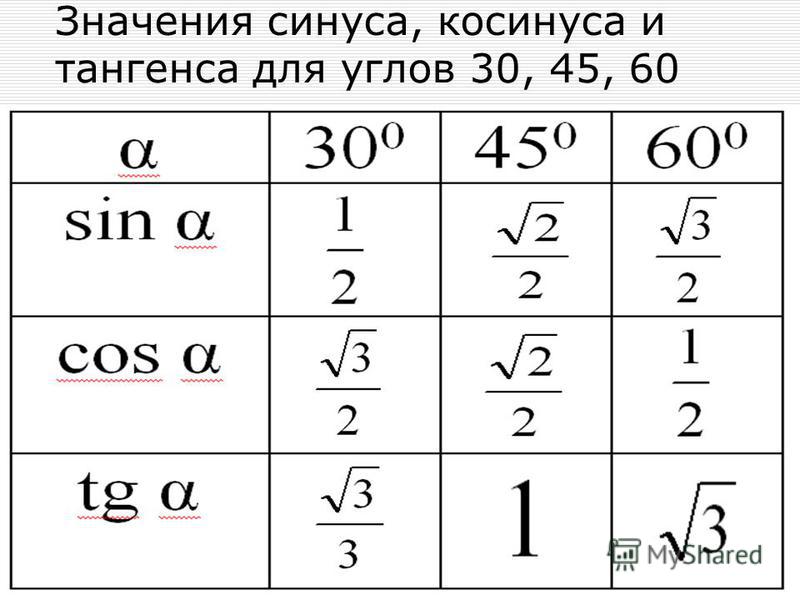
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Действительно ли дети понимают тригонометрию после введения синуса/косинуса/тангенса?
В этом году я много работал со своими детьми, занимающимися геометрией, чтобы у них сформировалось глубокое концептуальное понимание тригонометрии. Прямо сейчас мы все еще находимся в той части модуля, где термины синус/косинус/тангенс не были введены, и дети строят свое понимание, думая о соотношениях в определенных треугольниках. Но скоро мы собираемся ввести термины, и я боюсь, что они пойдут к своему калькулятору и будут использовать его вслепую, и забудут, что на самом деле означают синус, косинус и тангенс.
Для моих детей на этом уровне я хочу, чтобы каждый член был отношением, порождающим класс подобных треугольников, которые все выглядят одинаково, но имеют разные размеры. И я хочу, чтобы дети вызывали это в воображении, когда думают о… Но я боюсь, что 0,6428 перестанет терять смысл как отношение сторон… что 0,6428 ничего не будет значить для них ни геометрическое , ни визуальное .
Итак, вот подготовка к тому, что мы собираемся сделать.
Дети будут размещены парами. Им дадут следующую оценочную карту:
Им также дадут следующий лист с умным заголовком (платоническая часть относится к чему-то, о чем мы говорили раньше… не беспокойтесь об этом) ( .docx форма). На этом листе есть набор прямоугольных треугольников с углами 10, 20, 30, …, 80 градусов.
Затем со своим первым партнером на передней доске я проецирую:
У детей будет 3 минуты, чтобы обсудить, как они собираются выяснить, какие два треугольника/угла лучше всего «соответствуют» этим тригонометрическим уравнениям. (Я надеюсь, что в конце концов они скажут что-то вроде «Ну, гипотенуза должна быть примерно в два раза длиннее противоположного катета, так что это очень похоже на треугольник C на нашей салфетке» для первого уравнения.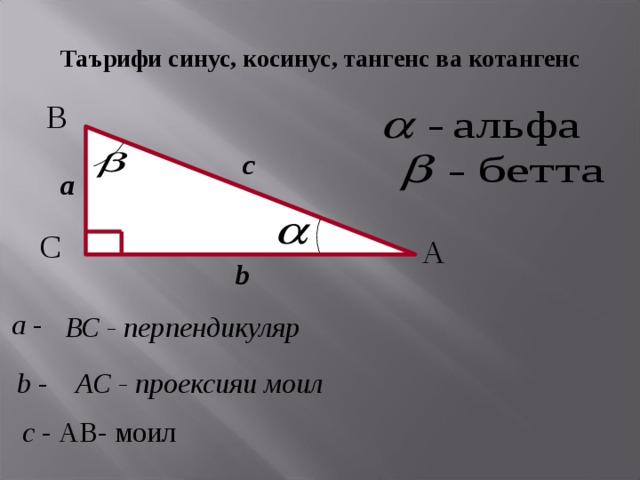
Они записывают свои ответы. Если они закончат раньше, у меня есть дополнительные контрольные вопросы с начала года, которые будут стоить некоторого количества баллов — над ними нужно работать индивидуально.
Когда время истекло, они пересаживаются на новый стул (особым образом), чтобы у каждого был новый партнер. Я подбрасываю некоторые другие уравнения. И попросите их обсудить и ответить. Затем они снова перемещаются и составляют новые уравнения.
Я построил уравнения, которые я составляю, определенным образом, поэтому я надеюсь, что они приведут к хорошим обсуждениям. И я надеюсь, что как только несколько человек поймут весь подход «давайте сравним длины сторон», переключение позволит продолжить обсуждение — так что скоро все это поймут.
В конце игры у нас будет обсуждение, и в ходе этих обсуждений мы найдем ответы. И, конечно же, учащийся, давший наибольшее количество правильных ответов, получит какой-нибудь сказочный приз.
Вопросы, которые я собираюсь задать, находятся здесь:
Просмотреть этот документ на Scribd
Вопросы для обсуждения находятся здесь:
Просмотреть этот документ на Scribd
Фин.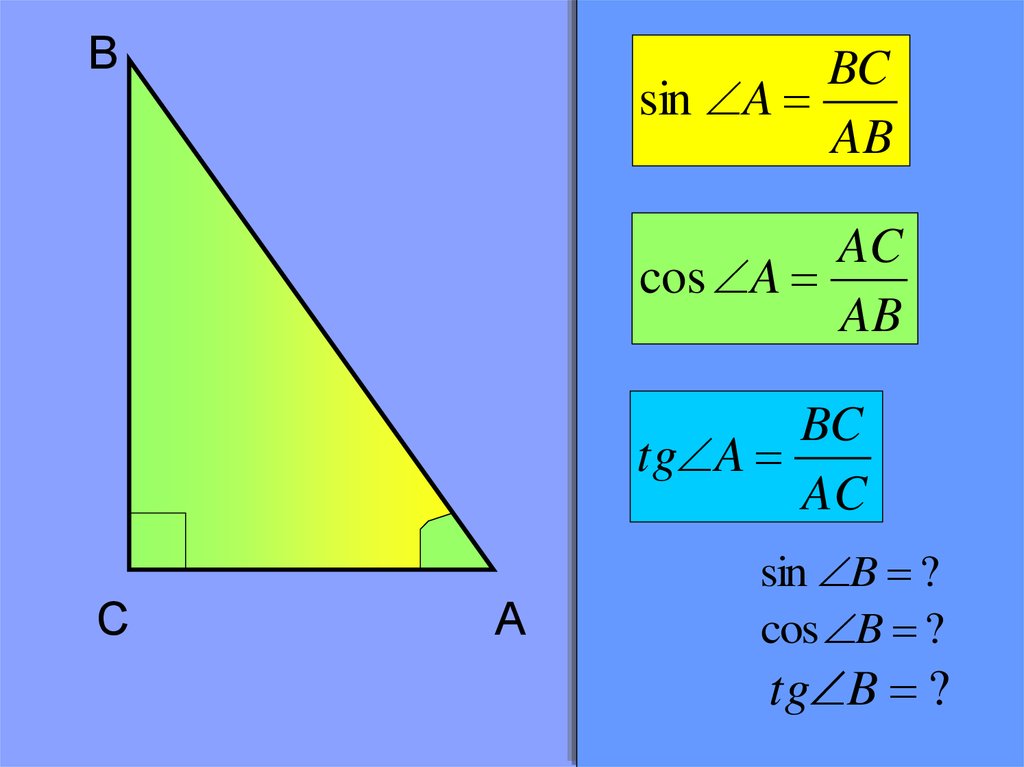
Я очень рад испытать это на своих детях на следующей неделе.
Нравится:
Нравится Загрузка…
Опубликовано 30 апреля 2015 г. автором samjshah в рубрике Без рубрики с тегами Геометрия. 16 комментариевМое резюме по визуальному обучению
Теги
Теги созданы благодаря усилиям @crstn85. Благодарю вас!
Геометрия
Алгебра II
Предварительное исчисление
Исчисление
Многомерное исчисление
Оценка на основе стандартов
Общие идеи для классной комнаты
Большие учебные вопросы
Хорошие математические задачи
Математическая связь
Другое
Архив блога
Архив блога Выберите месяц Август 2022 (3) Июль 2022 (3) Март 2022 (1) Ноябрь 2021 (1) Октябрь 2021 (1) Сентябрь 2021 (2) Октябрь 2020 (1) Август 2020 (1) Июль 2020 (1) Июнь 2020 ( 2) май 2020 г. (2) март 2020 г. (1) январь 2020 г. (2) октябрь 2019 г. (1) сентябрь 2019 г.
(3) июль 2019 г. (2) июнь 2019 г.(1) май 2019 г. (1) апрель 2019 г. (3) март 2019 г. (1) февраль 2019 г. (3) декабрь 2018 г. (1) ноябрь 2018 г. (1) сентябрь 2018 г. (1) август 2018 г. (4) июль 2018 г. (1) июнь 2018 г. (2) май 2018 г. (3) апрель 2018 г. (2) март 2018 г. (3) февраль 2018 г. (7) декабрь 2017 г. (1) октябрь 2017 г. (2) сентябрь 2017 г. (2) август 2017 г. (4) июль 2017 г. (1) июнь 2017 г. (2) май 2017 г. (1) апрель 2017 г. (5) март 2017 г. (1) февраль 2017 г. (2) январь 2017 г. (5) декабрь 2016 г. (1) ноябрь 2016 г. (2) октябрь 2016 г. (3) сентябрь 2016 г. (5) август 2016 г. (1) июль 2016 г. (3) июнь 2016 г. (3) май 2016 г. (4) апрель 2016 г. (4) март 2016 г. (2) февраль 2016 г. (1) январь 2016 г. (1) декабрь 2015 г. (1) ноябрь 2015 г. (2) октябрь 2015 г. (1) сентябрь 2015 г. (3) август 2015 г. (3) июль 2015 г. (1) июнь 2015 г. (1) май 2015 г. (3) апрель 2015 г. (2) март 2015 г. (4) февраль 2015 г. (2) январь 2015 г. (1) декабрь 2014 г. (1) октябрь 2014 г. (6) сентябрь 2014 г.
