6.2. Найти единичный вектор того же направления что и .
Единичный вектор находится: , где– модуль вектора.
Находим
тогда
Ответ: .
Примечание. Координаты единичного вектора должны быть не больше единицы.
6.3. Найти длину и направляющие косинусы вектора . Сравните с ответом в предыдущем пункте. Сделайте выводы.
Длина вектора – это есть его модуль:
, а направляющие косинусы мы можем найти по формуле одного из способов задания векторов:
Из полученного мы видим, что направляющие косинусы это и есть координаты единичного вектора.
Ответ: ,,,.
6.4. Найти .
Необходимо выполнить действия умножения вектора на число, сложения и модуль.
Почленно перемножаем координаты векторов на число.
Почленно складываем координаты векторов.
Находим модуль
вектора.
Ответ:
6.5. Определить координаты вектора , коллинеарного вектору, зная, чтои он направлен в сторону, противоположную вектору.
Вектор коллинеарен вектору, значит, его единичный вектор равен единичному векторутолько со знаком минус, т.к. направлен в противоположную сторону.
Единичный вектор имеет длину равную 1, значит, если его умножить на 5, то его длинна будет равна пяти.
Находим
Ответ:
6.6. Вычислить скалярные произведения и. Перпендикулярны ли векторыи,имежду собой?
Выполним скалярное произведение векторов.
Если вектора перпендикулярны, их скалярное произведение равно нулю.
Мы видим, что в нашем случае вектораиперпендикулярны.
Ответ: ,, векторы не перпендикулярны.
Примечание. Геометрический смысл скалярного
произведения малоприменим на практике,
но все-таки существует.
6.7. Найти работу, совершённую материальной точкой к которой приложена сила , при перемещении её из точки B в точку С.
Физический смысл скалярного произведения – это работа. Вектор силы здесь , вектор перемещения – это. А произведение этих векторов и будет искомой работой.
Находим работу
Ответ: -3.
6.8. Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC.
Из определения, скалярного произведения векторов получим формулу нахождения угла: .
Далее, нам нужно определить вектора, между которыми будем искать угол.
Внутренний угол будем искать как угол между векторами, выходящими из одной точки.
Для нахождения
внешнего угла нужно совмещать вектора,
таким образом, чтоб они выходили из
одной точки. Рисунок это поясняет.
Рисунок это поясняет.
Стоит заметить, что , только имеют разные начальные координаты.
Находим необходимые вектора и углы
Ответ: внутренний угол при вершине А = , внешний угол при вершине В =.
Вспомним вектора-орты: ,,.
Проекция находится также из скалярного произведения
–проекция b на a.
Ранее полученные нами вектора
, ,
Находим проекцию
Находим вторую проекцию
Ответ: ,
Примечание. Знак минуса при нахождении проекции означает то, что проекция опускается не на сам вектор, а в противоположную сторону, на линию на которой лежит этот вектор.
6.10. Вычислить .
Выполним векторное произведение векторов
Найдем модуль
Синус угла между векторами найдём из определения векторного произведения векторов
Ответ:
,,.
6.11. Найти площадь треугольника ABC и длину высоты, опушенной из точки С.
Геометрический смысл модуля векторного произведения состоит в том, что это площадь параллелограмма, образованного этими векторами. А площадь треугольника равна половине площади параллелограмма.
Площадь треугольника также можно найти как произведение высоты, на основание, делённое на два, из этого можно вывести формулу нахождения высоты.
Таким образом, найдём высоту
Ответ: ,.
6.12. Найти единичный вектор, перпендикулярный векторам и.
Результатом скалярного произведения есть вектор, который перпендикулярный двум исходным. А единичный вектор – это вектор, делённый на его длину.
Ранее, нами было найдено:
,
Ответ: .
6.13. Определить
величину и направляющие косинусы момента
силы
,
приложенной к А относительно точки С.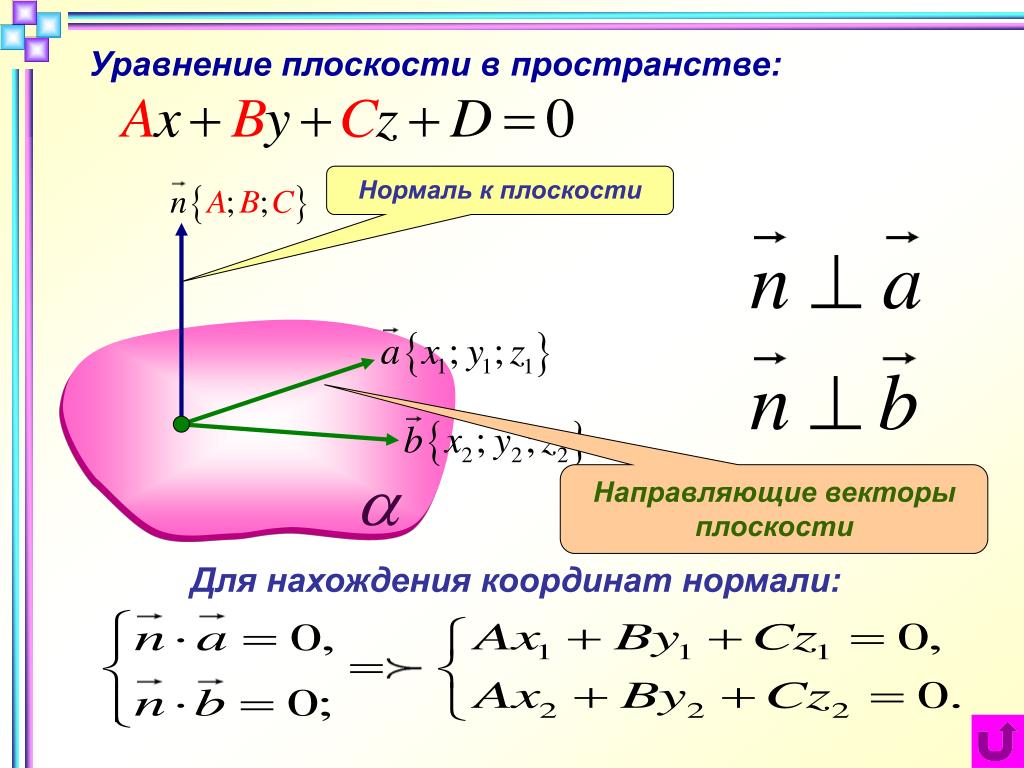
Физический смысл векторного произведения – это момент силы. Приведём иллюстрацию к данному заданию.
Находим момент силы
Ответ: .
6.14. Лежат ли векторы ,ив одной плоскости? Могут ли эти векторы образовывать базис пространства? Почему? Если могут, разложите по этому базису вектор.
Чтобы проверить лежат ли вектора в одной плоскости необходимо выполнить смешанное произведение этих векторов.
Смешанное произведение не равно нулю, следовательно, вектора не лежат в одной плоскости (не компланарные) и могут образовывать базис. Разложим по этому базису.
Разложим по базису, решив уравнение
Ответ: Векторы ,ине лежат в одной плоскости..
6.15. Найти . Чему равен объём пирамиды с вершинами A, B, C, D и её высота, опущенная из точки A на основание BCD.
Геометрический
смысл смешанного произведения в том,
что это объём параллелепипеда образованного
этими векторами.
Объём пирамиды, ещё можно найти так:
Получим формулу нахождения высоты
Находим
Находим высоту
Ответ: объём = 2.5, высота =.
6.16. Вычислить и.
–над этим заданием предлагаем вам подумать самим.
–выполним произведение.
Ранее было получено
Ответ: .
6.17. Вычислить
Выполним действия по частям
1)
2)
3)
4)
5)
Суммируем полученные значения
Ответ: .
6.18. Найти вектор , зная, что он перпендикулярен векторами, а его проекция на векторравна 5.
Разобьем данную задачу на две подзадачи
1) Найдём вектор, перпендикулярный векторам ипроизвольной длинны.
Перпендикулярный вектор мы получим в результате векторного произведения
Ранее, нами было найдено:
Искомый вектор отличается лишь длинной, от полученного
2) Найдем через уравнение
Ответ:
6. 19. Найти вектор
,
удовлетворяющий условиям,,.
19. Найти вектор
,
удовлетворяющий условиям,,.
Рассмотрим более детально данные условия.
Это система линейных уравнений. Составим и решим данную систему.
Ответ:
6.20. Определить координаты какого-либо вектора , компланарного с векторамии, и перпендикулярного вектору.
В данном задании два условия: компланарность векторов и перпендикулярность, выполним сначала первое условие, а потом второе.
1) Если вектора компланарны, значит их смешанное произведение равно нулю.
Отсюда получим некоторую зависимость координат вектора
Найдем вектор .
2) Если вектора перпендикулярны, значит их скалярное произведение равно нулю
Мы получили вторую зависимость координат искомого вектора
Для любого значения вектор будет удовлетворять условиям. Подставим.
Ответ: .
Аналитическая геометрия
Алгебра векторов, страница 21
Математика \ Аналитическая геометрия и линейная алгебра
Задачи
для самостоятельной работы.
1. Упростить выражение (a – b)xc – (a + с)xb – (b + с)xa.
2. Найти площадь треугольника, построенного на векторах 2m + n и 3m – n, если |m | = 4, , .
3. Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах
a = i – 2j + 2k и b = i – 3j + k.
4. Точки A(-2, 1, 3), B(-1, 3, 0), C(-4, 2, -1) являются вершинами ΔABC. Вычислить площадь треугольника и длину его высоты, опущенной из вершины С на сторону АВ.
5. Вектор a ортогонален оси Oz и вектору c = 2i – j + 3k,
образует с осью Oy острый угол и . Найти координаты вектора a.
6. Найти координаты вектора p, который ортогонален векторам a = (5, -2, 3) и c = (-1, 4, -3) и удовлетворяет условию , где b = 2
6. Сила F = 2i + j – 3k приложена к точке N(2, -5, 3). Найти момент этой силы относительно точки P(1, -3, -1).
7. Векторы a, b, c удовлетворяют условию a + b + c = 0. Доказать, что axb = bxc = cxa.
8. Найти координаты единичных векторов, перпендикулярных к плоскости ΔABC, построенного на векторах и .
9. Найти |(a – 3c)x(2a + c)|, если
векторы a и c ортогональны и |a| = 4, |c| = 3.
10. Найти площадь параллелограмма, диагоналями которого являются векторы 3m + 2n и
-5m + 4n, если , |n| = 2, .
11. Найти координаты единичного вектора p, перпендикулярного векторам a = i – 2j и
c = 2j + 3k и образующего с осью Oz тупой угол.
12. Даны векторы a = 2i + 6j – 3k, b = i + 5j – k, c = –i – 3j + 2k. Найти координаты вектора p, ортогонального векторам b и c, если .
13. Вычислить площадь треугольника с вершинами в точках A(2, -2, 3), B(3, -3, 4), C(1, 0, 1) и длину его высоты, опущенной из вершины B на сторону AC.
14. Найти площадь
параллелограмма, построенного на векторах m = 2a — c и
Найти площадь
параллелограмма, построенного на векторах m = 2a — c и
n = a + 3c, если .
15. Сила f = (1, -2, 3) приложена к точке P(3, 1, 1). Найти момент этой силы относительно точки A(2, 0, 2).
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Найдите единичный вектор, перпендикулярный плоскости треугольника ABC, где координаты его вершин равны A(3, –1,2), B(1, –1, –3) и C(4, –3, 1) . — Sarthaks eConnect
← Предыдущий вопрос Следующий вопрос →
спросил в векторах по Рупа01 (32,5 тыс. баллов)закрыто от Rupa01
Найдите единичный вектор, перпендикулярный плоскости треугольника ABC, где координаты его вершин равны A(3, –1, 2), B(1, –1, –3) и C(4, –3, 1) .
- векторная алгебра
- класс-12
1 ответ
+1 голос
← Предыдущий вопрос Следующий вопрос →
Похожие вопросы
Если вектор a, вектор b, вектор c являются векторами положения вершин A, B и C соответственно треугольника ABC, запишите значение вектора (AB)
спросил 16 мая 2021 г. в векторах по Лакхи (29,5 тыс. баллов)
- векторная алгебра
- класс-12
Вершины A, B, C треугольника ABC имеют соответственно векторы положения вектор a, вектор b, вектор c относительно данного начала координат O.
спросил 13 мая 2021 г. в векторах по Каина (30,5 тыс. баллов)
- векторная алгебра
- класс-12
Если вершины A, B, C треугольника ABC являются точками с векторами положения a1 i+a2 j + a3 k, b1i + b2 j + b3k, c2j +c3k
спросил
14 мая 2021 г. в векторах
по
Лакхи
(29,5 тыс. баллов)
в векторах
по
Лакхи
(29,5 тыс. баллов)
- векторная алгебра
- класс-12
Если вершины A, B, C треугольника ABC равны (1, 2, 3), (-1, 0, 0), (0, 1, 2) соответственно,
спросил 26 февр. 2020 г. в векторах по Звуковой сигнал (59,1 тыс. баллов)
- векторная алгебра
- класс-12
Напишите единичный вектор, образующий равные острые углы с осями координат.
спросил 16 мая 2021 г. в векторах по Лакхи (29,5 тыс. баллов)
- векторная алгебра
- класс-12
Категории
- Все категории
- JEE (28,1к)
- NEET (8,5к)
- Наука (748к)
- Математика
(242к)
- Система счисления (9,8к)
- Множества, отношения и функции (5,5к)
- Алгебра (35,9к)
- Коммерческая математика (7,4к)
- Координатная геометрия (10,4к)
- Геометрия (11,7к)
- Тригонометрия (11,0 к)
- Измерение (6,8к)
- Статистика (4,9к)
- Вероятность (5,3к)
- Векторы (2,8к)
- Исчисление (19,7к)
- Линейное программирование (909)
- Статистика (2,8к)
- Наука об окружающей среде (3,8к)
- Биотехнология (579)
- коммерция (62,4к)
- Электроника (3,7к)
- Компьютер (16,3к)
- Искусственный интеллект (ИИ) (1,4к)
- Информационные технологии (13,2к)
- Программирование
(8.
 7к)
7к) - Политическая наука (6,5к)
- Домашняя наука (4,9к)
- Психология (3,4к)
- Социология (5,6к)
- Английский (58,3к)
- хинди (23,6к)
- Способность (23,7к)
- Рассуждение (14,6к)
- ГК (25,7к)
- Олимпиада (527)
- Советы по навыкам (75)
- CBSE (722)
- РБСЭ (49,1к)
- Общий (58,5к)
- МСБШСЭ (1,8к)
- Совет Тамилнаду (59,3к)
- Совет Кералы (24,5к)
математика — Как найти координаты трехмерных точек в плоскости, перпендикулярной заданному вектору
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 531 раз
У меня есть две точки в трехмерном пространстве, одна точка (x,0,z), а другая — начало координат (0,0,0), через эти точки проходит линия длиной L, которая начинается от первой точки и продолжая за исходной точкой, в конце этой линии находится перпендикулярная (к линии) плоская доска размерами Ш х В, линия заканчивается посередине этой доски.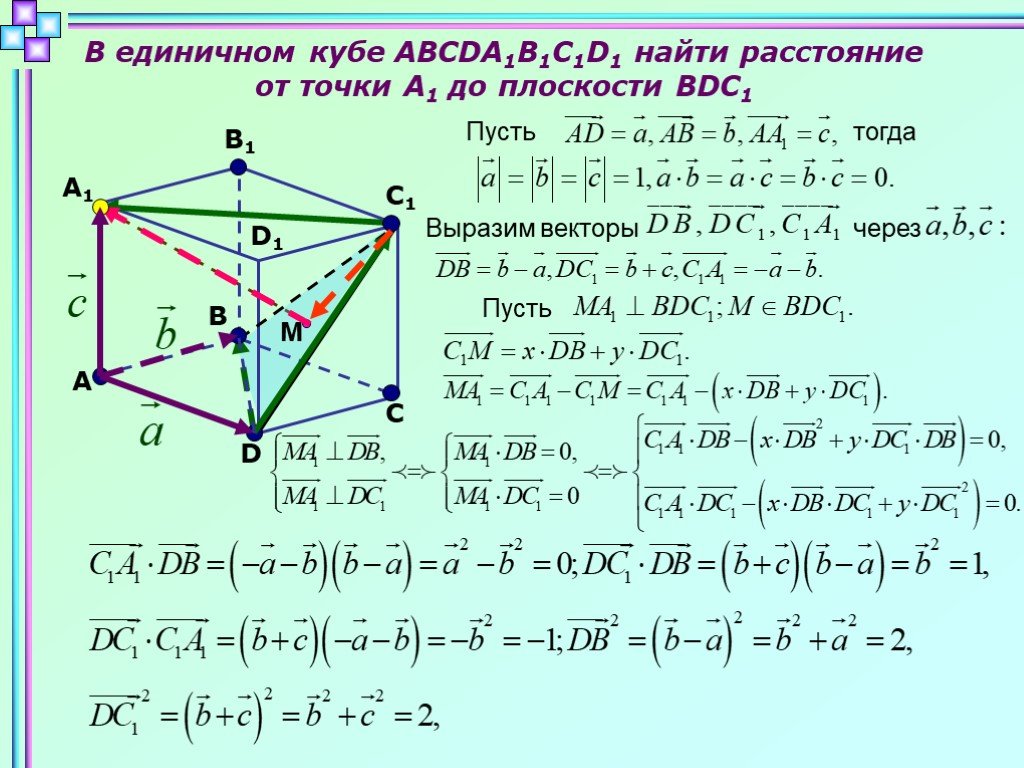
Предположим, что x, z, L, H, W заданы. Мне нужен способ найти все координаты трехмерных точек, где эти точки образуют изображение в пикселях на доске (это означает, что каждая точка имеет расстояние 1 слева от нее, правая, верхняя, нижняя соседние точки).
Прикрепил довольно некрасивый рисунок 🙂 Сделал, пытаясь проиллюстрировать проблему (точки пикселей отметил двумя вопросительными знаками, а мне нужны они все).
Спасибо.
- математика
- вектор
- геометрия
- вычислительная геометрия
- векторная графика
0
Можно определить эту плоскость. Но нет выбранного направления для однозначного построения сетки.
В качестве основы выберем направление OY (потому что нормаль имеет нулевую Y-компоненту).
Итак, мы имеем:
Вектор нормали N = (xx, 0, zz) //Я переименовал значения, чтобы не путать с координатой
переменные
Единичный вектор нормали n = (nx, 0, nz) , где
nx = xx / Sqrt(xx*xx+zz*zz) nz = zz / Sqrt(xx*xx+zz*zz)
Базовая точка
B = (bx, 0, bz) = (xx - nx * L, 0, zz - nz * L)
Базовый вектор единицы измерения в плоскости
dy = (0, 1, 0)
Другой базовый вектор
dc = dy x n // векторное произведение = (-бз, 0, бх)
Теперь можно генерировать сетку, используя целочисленные индексы i, j в диапазонах (-W/2.

 Даля 166
Даля 166 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123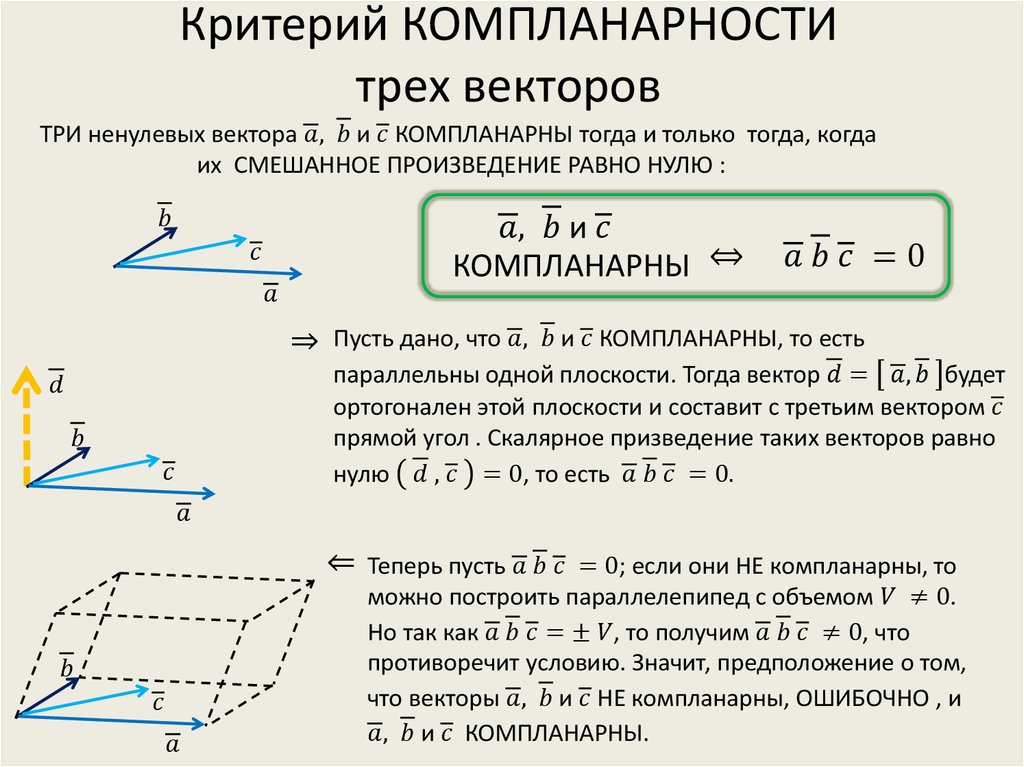 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305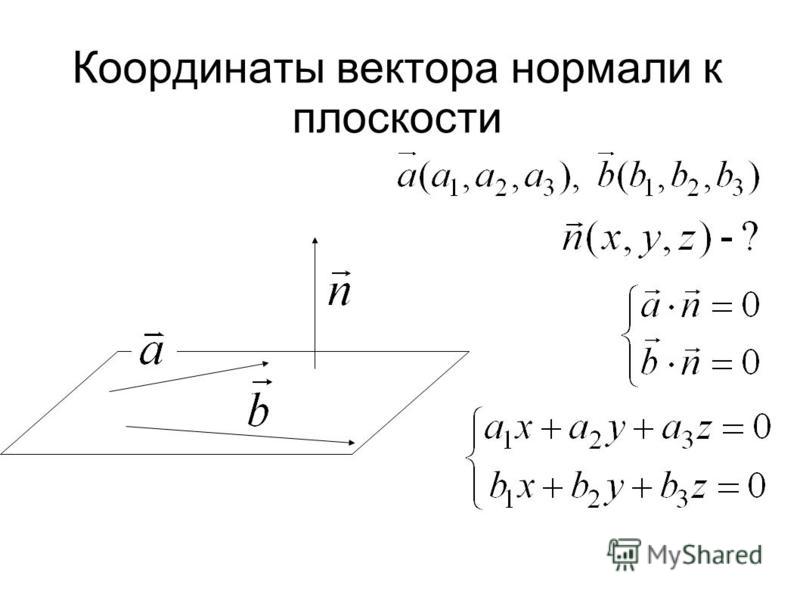 7к)
7к)