Кубический корень числа Калькулятор | Вычислить Кубический корень числа
✖Число X — это действительное число, которое можно использовать для вычисления общих формул чисел.ⓘ Номер Х [X] | +10% -10% |
|
✖Кубический корень числа — это значение, которое при трехкратном или трехкратном умножении само на себя дает исходное число.ⓘ Кубический корень числа [X1/3] |
⎘ копия |
👎
Формула
сбросить
👍
Кубический корень числа Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
(1/3) 4 = 0, что может быть легче решить. 3) Кубический корень можно использовать в различных приложениях в науке, технике и других областях. Например, в физике кубический корень из объема используется для вычисления объема куба с заданной длиной стороны. В финансах кубический корень из цены акции используется для расчета отношения цены акции к прибыли.
Share
Copied!
Алгебра. Учебник для 6-8 классов
Алгебра. Учебник для 6-8 классов
ОглавлениеГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.§ 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14.  Законы сложения.§ 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень.  § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ.  § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. § 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 79. Равносильные системы.  (1/3)§ 130. Примеры графического решения уравнений и систем уравнений. |
Переработка учебника и изложение вопросов, вновь включенных в программу восьмилетней школы, выполнены С.И. Новоселовым.
Видео-урок: Кубические корни рациональных чисел
Стенограмма видео
В этом видео мы научимся найти кубические корни рациональных чисел.
Начнем с того, что вспомним, что мы знать о кубическом корне из совершенного куба. Кубический корень из совершенного куба 𝑛, записанное, как показано, является целым числом 𝑎 таким, что 𝑎 в кубе равно 𝑛. В частности, у нас есть куб корень из 𝑛 равен кубическому корню из 𝑎 в кубе, который равен 𝑎.
Теперь рассмотрим полезный
свойство кубического корня числа, рассматривая произведение двух совершенных
кубики. Это утверждает, что если 𝑎 и 𝑏 равны
целые числа, то кубический корень из 𝑎 в кубе 𝑏 в кубе равен 𝑎𝑏. Мы можем доказать это следующим образом.
Когда мы возьмем 𝑎 в куб, умноженный на 𝑏,
мы получаем 𝑎 в кубе 𝑏 в кубе. А это значит, что 𝑎𝑏 — это
кубический корень из 𝑎 в кубе 𝑏 в кубе. Мы можем использовать аналогичную идею для расширения
это определение кубического корня, чтобы взять кубические корни из частных
целые числа. Если 𝑎 и 𝑏 — целые числа, а 𝑏 —
не равен нулю, то кубический корень из 𝑎 в кубе над 𝑏 в кубе равен кубу
корень из 𝑎 в кубе над кубическим корнем из 𝑏 в кубе, который равен 𝑎 над 𝑏. Сейчас мы рассмотрим пример
где нам нужно использовать это свойство для определения кубического корня рационального
количество.
Вычислите кубический корень из 64 по 343.
В этом вопросе мы пытаемся
найти кубический корень из рационального числа. Напомним, что если 𝑎 и 𝑏 равны
целые числа и 𝑏 не равно нулю, то кубический корень из 𝑎 над 𝑏 равен кубическому
корень из 𝑎 над кубическим корнем из 𝑏.
В нашем следующем примере мы определить кубический корень из рационального числа, заданного в десятичной форме.
Найдите значение кубического корня из
0,027.
Чтобы ответить на этот вопрос,
мы рассмотрим два метода. В первом мы начнем с
преобразование десятичной дроби в дробь. Используя наши знания о значении места,
мы знаем, что 0,027 — это то же самое, что и двадцать семь тысячных. Это означает, что мы пытаемся
вычислить кубический корень из двадцати семи тысячных. Далее напомним, что если 𝑎 и 𝑏
являются целыми числами и 𝑏 не равно нулю, то кубический корень из 𝑎 над 𝑏 равен
кубический корень из 𝑎 над кубическим корнем из 𝑏. Таким образом, мы можем вычислить куб
корень из 27 и кубический корень из 1000 отдельно. Так как три в кубе равно 27,
кубический корень из 27 равен трем. Аналогично, поскольку 10 в кубе равно 1000,
кубический корень из 1000 равен 10. Кубический корень из 27, деленный на
поэтому кубический корень из 1000 равен трем десяти или трем десятым. И это значение куба
корень из 0,027.
Теперь рассмотрим второй метод, который мы могли бы использовать для решения этой проблемы. Начнем с того, что запишем 0,027 как 27. умножить на 0,001. Как уже упоминалось, 27 равно до трех куб. Точно так же 0,001 равно 0,1 куб. Поэтому мы можем переписать исходное выражение, как показано. Используя тот факт, что кубический корень 𝑎 в кубе 𝑏 в кубе равно 𝑎𝑏, мы можем переписать правую часть нашего уравнение как три, умноженные на 0,1, что еще раз дает нам окончательный ответ 0,3.
В нашем следующем примере мы определить длину стороны куба по его объему.
Найдите длину стороны куба при том, что его объем составляет 27 на восемь кубических сантиметров.
Начнем с того, что вспомним, что куб
со стороной 𝑙 сантиметров будет иметь объем 𝑙 кубических сантиметров.
Это означает, что в этом вопросе
𝑙 в кубе равно 27 на восемь или двадцать семь восьмых. Заметим, что и 27, и восемь
совершенные кубы, так как три в кубе равно 27, а два в кубе равно восьми. Поэтому мы можем переписать наш
уравнение как 𝑙 в кубе равно трем в кубе на два в кубе. Для ее решения возьмем
кубический корень из обеих сторон. Напоминая, что если 𝑎 и 𝑏 равны
целые числа и 𝑏 не равно нулю, то кубический корень из 𝑎 в кубе над 𝑏 в кубе равен
𝑎 над 𝑏. Затем правая часть нашего
уравнение упрощается до трех вместо двух. И поэтому мы можем сделать вывод, что
длина стороны куба объемом 27 больше восьми кубических сантиметров равна трем
более двух сантиметров. Также стоит отметить, что мы могли
запишите это в десятичной форме 1,5 сантиметра.
В последнем примере этого видео
мы будем определять радиус сферы по ее объему.
Предположим, что значение 𝜋 равно 22 больше семи, найдите радиус сферы, если ее объем равен 179,6 куб. сантиметры.
Начнем с того, что вспомним формулу
для объема шара. Равно четырем третям 𝜋𝑟
в кубе. В этом вопросе нам говорят, что
объем равен 179.6 повторяющихся кубических сантиметров. Мы знаем, что повторение 0,6 равно
до дроби две трети. Это означает, что объем
сферу можно переписать как 179 и две трети кубических сантиметров. Мы можем преобразовать это смешанное число
в неправильную или тяжелую дробь. Мы делаем это, умножая все
числа по знаменателю, а затем прибавить числитель. 179 умножить на три плюс два равно
равно 539. Объем сферы
поэтому равно 539 на три кубических сантиметра. Подставив это значение в наш
формула вместе со значением 𝜋 22 на семь, мы имеем 539 на три
равно четырем третям, умноженным на 22 на семь, умноженным на 𝑟 в кубе.
Упрощение правой части
дает нам 88 на 21 𝑟 в кубе.
Далее мы можем умножить на три таких, что 539равно 88 на семь 𝑟 в кубе. Деление на 88 на семь а затем деление числителя и знаменателя на 11 дает нам 𝑟 в кубе равно 343 больше восьми. Тогда мы можем извлечь кубический корень из обе части этого уравнения. Отметив, что 343 и восемь совершенных кубов, так как два в кубе равно восьми, а семь в кубе равно 343, мы 𝑟 равно кубическому корню из семи в кубе над двумя в кубе. Напомним одно из свойств кубические корни, что если 𝑎 и 𝑏 целые числа, а 𝑏 не равно нулю, кубический корень из 𝑎 в кубе над 𝑏 в кубе равно 𝑎 над 𝑏, это означает, что 𝑟 равно семи более двух, что в десятичной форме равно 3,5. Если объем шара 179.6 повторяющихся кубических сантиметров, то его радиус равен 3,5 сантиметра.
Сейчас мы закончим это видео,
повторение ключевых моментов.
Мы видели в этом видео, что если 𝑎 и
𝑏 — целые числа, то кубический корень из 𝑎 в кубе 𝑏 в кубе равен 𝑎𝑏. Точно так же, если 𝑎 и 𝑏 равны
целые числа и 𝑏 не равно нулю, то кубический корень из 𝑎 в кубе над 𝑏 в кубе
равно 𝑎 над 𝑏. Мы также видели, что в некоторых вопросах
нам может понадобиться факторизовать числитель и знаменатель, чтобы определить их куб
корни. В последних двух примерах мы использовали
кубические корни для геометрических приложений, чтобы вычислить длину стороны
куб и радиус сферы.
Как найти кубические корни и совершенные кубики
Как найти кубические корни и совершенные кубики
Jana Russick
13 мая 2021
Онлайн -репетитор чтобы найти кубические корни, вы должны просмотреть квадратные корни. Нахождение квадратного корня числа означает определение того, какое другое число нужно умножить само на себя, чтобы получить исходное число.
Например:
√81 = 9
Что такое кубические корни?
Нахождение кубических корней делает еще один шаг вперед. Ниже приведен пример числа, возводимого в куб:
4³ = 64
4 x 4 x 4 = 64
пример 64 снова. Чтобы найти его кубический корень, вам нужно знать, что 4 нужно умножить само на себя три раза, чтобы получить окончательный результат 64.
Если вы хотите вычислить кубический корень, вы должны указать маленькую 3 вне символа корня:
³√8 = 2
Нахождение кубического корня из отрицательных чисел
В отличие от квадратных корней, вы можете извлечь кубический корень из отрицательного числа. Это потому, что отрицательное число, умноженное само на себя 3 раза, всегда будет равно отрицательному. Из-за этого результат кубирования числа не обязательно должен быть целым числом, это может быть отрицательное или положительное число:
³√-216 = 6
Что такое идеальный куб?
Теперь, когда мы узнали, как находить кубический корень числа, давайте рассмотрим совершенные кубы.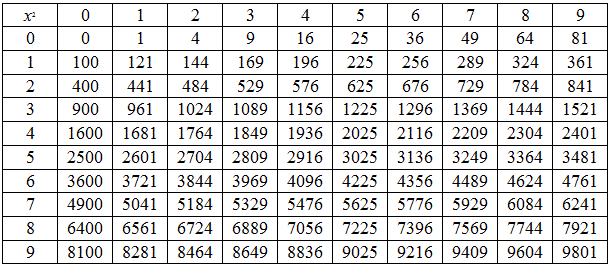
Используя калькулятор кубического корня, вы технически можете извлечь кубический корень из любого числа. Тем не менее, иногда вы будете получать ответ, содержащий множество десятичных знаков. Но этого не происходит, когда вы берете кубический корень из совершенного куба.
Совершенный куб — это целое число, которое получится, если возвести другое целое число в третью степень. Целое число в виде совершенного куба не может быть десятичной дробью или дробью. То же самое касается числа, которое возводится в третью степень.
Вот список идеальных кубиков:
1³ = 1
2³ = 4
3³ = 27
4³ = 64
5³ = 125
6³ = 216
73 = 343
. удобно, когда у вас нет калькулятора кубического корня.
Как находить кубические корни
Нахождение кубических корней — это просто применение того, что вы узнали о квадратных корнях, и продвижение вперед. Таким образом, вместо двукратного умножения числа само на себя кубирование — это процесс трехкратного умножения числа на самого себя.