Найти наибольшее и наименьшее значение функции на отрезке
Онлайн калькулятор поможет найти наибольшее и наименьшее значение функции на отрезке.
Наибольшее значение функции y=f(x) – это значение maxx∈X y=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Наименьшее значение функции y=f(x) – это значение minx∈X y=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(x)≥f(x0).
Наибольшее и наименьшее значение непрерывной функции f(x) на промежутке a,b достигаются в критических точках, то есть в точках в которых производная функции равна нулю f′(x)=0, бесконечности f′(x)=±∞, не существует, либо на концах отрезка a,b.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
Смотрите также
Как найти наибольшее и наименьшее значения функции на отрезке.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции 
 , то функция
, то функция  возрастает на этом промежутке.
возрастает на этом промежутке.
Если на промежутке I производная функции 
 , то функция
, то функция  убывает на этом промежутке.
убывает на этом промежутке.
5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с «+» на «-«.
В точке минимума функции производная меняет знак с «-» на «+».
6. Находим значение функции в концах отрезка,
- затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
- или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию  . График этой функции выглядит так:
. График этой функции выглядит так:
 В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;0}{]} {x}{in}delim{[}{-1;0}{]}](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_8d4ac2719ab1423f162f9779293da981.png)
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка:  , а наименьшее — в левом:
, а наименьшее — в левом:  .
.
2. Рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;1}{]} {x}{in}delim{[}{-1;1}{]}](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_fbae2bb0d6eaada0859d11280c8d6a23.png)
Очевидно, что наибольшее значение функция принимает в точке максимума  , а наименьшее — в одном из концов отрезка, то есть надо найти значения
, а наименьшее — в одном из концов отрезка, то есть надо найти значения  и
и  и выбрать из них наименьшее.
и выбрать из них наименьшее.
3. Если мы рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;2}{]} {x}{in}delim{[}{-1;2}{]}](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_3bae536560f42bd0f0875793dd5a92e2.png)
 и
и  .
.Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть  и
и 
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции  — множество действительных чисел.
— множество действительных чисел.
2. 
3.  , если
, если  или
или 
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
1. Задание B15 (№ 26695)
Найдите наибольшее значение функции  на отрезке
на отрезке ![[-{pi}/2;0] [-{pi}/2;0]](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_9a7375f1961203c68e53ad122ab84a77.png) .
.
1. Функция  определена при всех действительных значениях х
определена при всех действительных значениях х
2. 
3. 
 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция  возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
y(0)=5
Ответ: 5.
2. Задание B15 (№ 26702)
Найдите наибольшее значение функции  на отрезке [
на отрезке [ ].
].
1. ОДЗ функции 

2. 
Производная равна нулю при  , однако, в этих точках она не меняет знак:
, однако, в этих точках она не меняет знак:

 , следовательно,
, следовательно, 
 , значит,
, значит, 
 , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция
, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция  возрастает и принимает наибольшее значение в правом конце промежутка, при
возрастает и принимает наибольшее значение в правом конце промежутка, при  .
.
Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

у(0)=5
Ответ: 5.
3. Задание B15 (№ 26708)
Найдите наименьшее значение функции  на отрезке [
на отрезке [ ].
].
1. ОДЗ функции  :
: 

2. 
3. 
 ,
, 
Расположим корни этого уравнения на тригонометрической окружности.

Промежутку ![delim{[}{-{pi}/3;{pi}/3}{]} delim{[}{-{pi}/3;{pi}/3}{]}](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_e5f186d35c95dd888150972e98bd371a.png) принадлежат два числа:
принадлежат два числа:  и
и 
Расставим знаки. Для этого определим знак производной в точке х=0: 
 . При переходе через точки
. При переходе через точки  и
и  производная меняет знак.
производная меняет знак.

Изобразим смену знаков производной функции  на координатной прямой:
на координатной прямой:

Очевидно, что точка  является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции
является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции  на отрезке
на отрезке ![delim{[}{-{pi}/3;{pi}/3}{]} delim{[}{-{pi}/3;{pi}/3}{]}](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_e5f186d35c95dd888150972e98bd371a.png) , нужно сравнить значения функции в точке минимума и в левом конце отрезка,
, нужно сравнить значения функции в точке минимума и в левом конце отрезка,  .
.
Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а  таковым на является, следовательно подставим в уравнение функции
таковым на является, следовательно подставим в уравнение функции 

Ответ: -1
Вероятно, Ваш браузер не поддерживается. Попробуйте скачатьFirefox
И.В. Фельдман, репетитор по математике.



Наименьшее значение функции онлайн · Как пользоваться Контрольная Работа РУ
Чтобы найти наименьшее значение заданной функции, то стоит воспользоваться сервисом на сайте «Контрольная работа РУ».
На примере функции 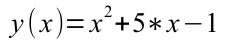
как можно найти наименьшее значение онлайн.
Итак:
1. Вам нужно перейти на страницу сервиса по исследованию функций онлайн и построения графиков.
2. Для указанного примера вбиваем функцию x^2 + 5*x — 1 в форму:

3. После того как вбили функцию, для которой надо найти наименьшее значение, то нажимаем кнопку «Найти наименьшее значение!»
4. Ждём, когда сервер произведёт исследование функции (1-2 сек) и вы увидите результат данного исследования. В том числе там будет подробное решение по нахождению наименьшего значения функции. Я скопировал часть результата исследования для моего примера, которая связана с вычислением минимального значения функции:
- Экстремумы функции:
- Для того, чтобы найти экстремумы, нужно решить уравнение y’=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y'=2*x + 5=0
Решаем это уравнение и его корни будут экстремумами:- x=-5/2. Точка: (-5/2, -29/4)
- Интервалы возрастания и убывания функции:
- Найдем интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим на ведет себя функция в экстремумах при малейшем отклонении от экстремума:
- Минимумы функции в точках:
- Максимумов у функции нету
- Возрастает на промежутках: [-5/2, oo)
- Убывает на промежутках: (-oo, -5/2]
Видим, что наименьшее значение функции для моего примера найдено и равно y min = -5/2 = — 2.5
Решаем задачи B14 из ЕГЭ
Автор Сергей Валерьевич
Воскресенье, 18 декабря, 2011
В задании B14 из ЕГЭ по математике требуется найти наименьшее или наибольшее значение функции одной переменной. Это достаточно тривиальная задача из математического анализа, и именно по этой причине научиться решать её в норме может и должен каждый выпускник средней школы. Разберём несколько примеров, которые школьники решали на диагностической работе по математике, прошедшей в Москве 7 декабря 2011 года.
В зависимости от промежутка, на котором требуется найти максимальное или минимальное значение функции, для решения этой задачи используется один из следующих стандартных алгоритмов.
I. Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Выбрать из точек, подозрительных на экстремум, те, которые принадлежат данному отрезку и области определения функции.
- Вычислить значения функции (не производной!) в этих точках.
- Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 1. Найдите наименьшее значение функции
y = x3 – 18x2 + 81x + 23 на отрезке [8; 13].
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
- Область определения функции не ограничена: D(y) = R.
- Производная функции равна: y’ = 3x2 – 36x + 81. Область определения производной функции также не ограничена: D(y’) = R.
- Нули производной: y’ = 3x2 – 36x + 81 = 0, значит x2 – 12x + 27 = 0, откуда x = 3 и x = 9, в наш промежуток входит только x = 9 (одна точка, подозрительная на экстремум).
- Находим значение функции в точке, подозрительной на экстремум и на краях промежутка. Для удобства вычислений представим функцию в виде: y = x3 – 18x2 + 81x + 23 = x(x-9)2+23:
- y(8) = 8 · (8-9)2+23 = 31;
- y(9) = 9 · (9-9)2+23 = 23;
- y(13) = 13 · (13-9)2+23 = 231.
Итак, из полученных значений наименьшим является 23. Ответ: 23.
II. Алгоритм нахождения наибольшего или наименьшего значения функции:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Отметить эти точки и область определения функции на числовой прямой и определить знаки производной (не функции!) на получившихся промежутках.
- Определить значения функции (не производной!) в точках минимума (те точки, в которых знак производной меняется с минуса на плюс), наименьшее из этих значений будет наименьшим значением функции. Если точек минимума нет, то у функции нет наименьшего значения.
- Определить значения функции (не производной!) в точках максимума (те точки, в которых знак производной меняется с плюса на минус), наибольшее из этих значений будет наибольшим значением функции. Если точек максимума нет, то у функции нет наибольшего значения.
Пример 2. Найдите наибольшее значение функции: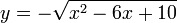 .
.
Решение: действуем по алгоритму нахождения наибольшего значения функции:
- Область определения функции задается неравенством:
 , которое выполняется при любом x, поскольку ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратного трехчлена отрицателен: D(y) = R.
, которое выполняется при любом x, поскольку ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратного трехчлена отрицателен: D(y) = R. - Производная функции равна:
 ,
,
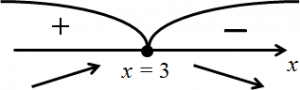
область определения которой также не ограничена, поскольку по указанной выше причине x2 – 6x + 10 > 0, и знаменатель дроби нигде не обращается в ноль: D(y’) = R. - Нули производной: 2x — 6 = 0, откуда x = 3 (одна точка, подозрительная на экстремум).
- Отмечаем область определения функции и точки, подозрительные на экстремум, на числовой прямой, определяем знаки производной в получившихся промежутках:
 x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.
x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке. - Находим это значение:
 .
.
Итак, наибольшее значение функции равно -1. Ответ: -1.
Репетитор по математике
Сергей Валерьевич
Найдите наименьшее из двух чисел с помощью Java —
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Найдите наименьшее число в списке Python и распечатайте позицию
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
нахождение наименьшего и второго наименьшего значения массива в C ++
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
— как найти наименьшее число, состоящее только из 0 и 1, которое делится на заданное число?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании

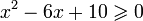 , которое выполняется при любом x, поскольку ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратного трехчлена отрицателен: D(y) = R.
, которое выполняется при любом x, поскольку ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратного трехчлена отрицателен: D(y) = R.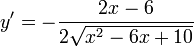 ,
, x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.
x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.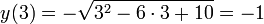 .
.