Найти объем пирамиды по векторам: Объем пирамиды, построенной на векторах онлайн

Алгебра векторов, страница 24

Математика \ Аналитическая геометрия и линейная алгебра

= 5|(2a, a x c) + (b, a x c) – (c, (a x c)|. Так как смешанное произведение, в котором два одинаковых вектора, равно нулю, то V = 5|(b, a x c)|. Поскольку a x c  a, a x c  c, то a x c || b и  векторы a x c и b сонаправлены (тройка векторов — правая), угол между ними равен нулю, и . Но . Окончательно получим .

Пример 2. Найти объём треугольной пирамиды SABC, образованной векторами , ,  и длину её высоты, опущенной на грань ABS.

Решение. Объём треугольной пирамиды

. Находим площадь ΔABC: .

Найдём векторное произведение , следовательно .

С другой стороны объём треугольной пирамиды находим по формуле:

.

Пример 3. Доказать, что точки А(2, 3, -1), B(1, 2, 5), C(4, 3, -3), D(3, 2, 3) принадлежат одной плоскости.

Решение. Найдем векторы , , . Точки принадлежат одной плоскости тогда и только тогда, когда векторы ,  и  компланарные. Вычислим смешанное произведение этих векторов:

. Следовательно, векторы ,  и   компланарны, то есть точки A, B, C, D принадлежат одной плоскости.

Задачи для самостоятельной работы.

1. Найти объём параллелепипеда, построенного на векторах a = m + n, b = 2p — n,

 c = p + 2n + 3m, если взаимно ортогональные векторы m, n, p

  образуют левую тройку векторов и |m| = 2, |n| = 3, |p| = 2.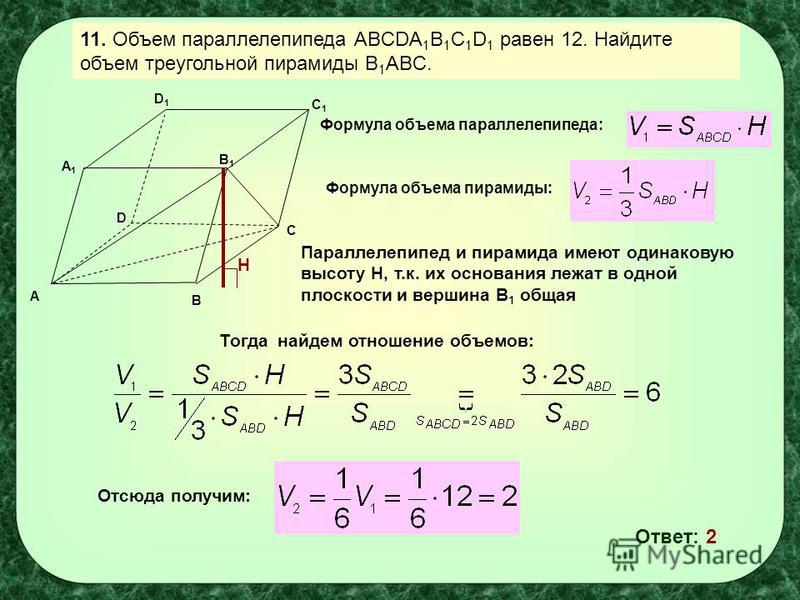

2. Треугольная пирамида задана радиусами- векторами своих вершин r_A= (0, 1, 2),

r_B= (1, 3, 1), r_C= (2, -2, 0) и r_S= (-4, -1, 3). Определить объём пирамиды и длину высоты, опущенной на грань ASB.

3. Показать, что точки А(1, -3, 2), B(-1, -2, 3), C(2, -5, 5), D(15, -16, 9) лежат в одной плоскости.

4. В основании четырёхугольной пирамиды SABCD лежит параллелограмм ABCD, построенный на векторах  и . Задано боковое ребро  и точка F делит сторону BS в отношении 1:2. Вычислить объём пирамиды ABDF.

Скачать файл

Выбери свой ВУЗ

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им.
  Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Векторное произведение векторов и его свойства (Лекция №18)

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ И ЕГО СВОЙСТВА

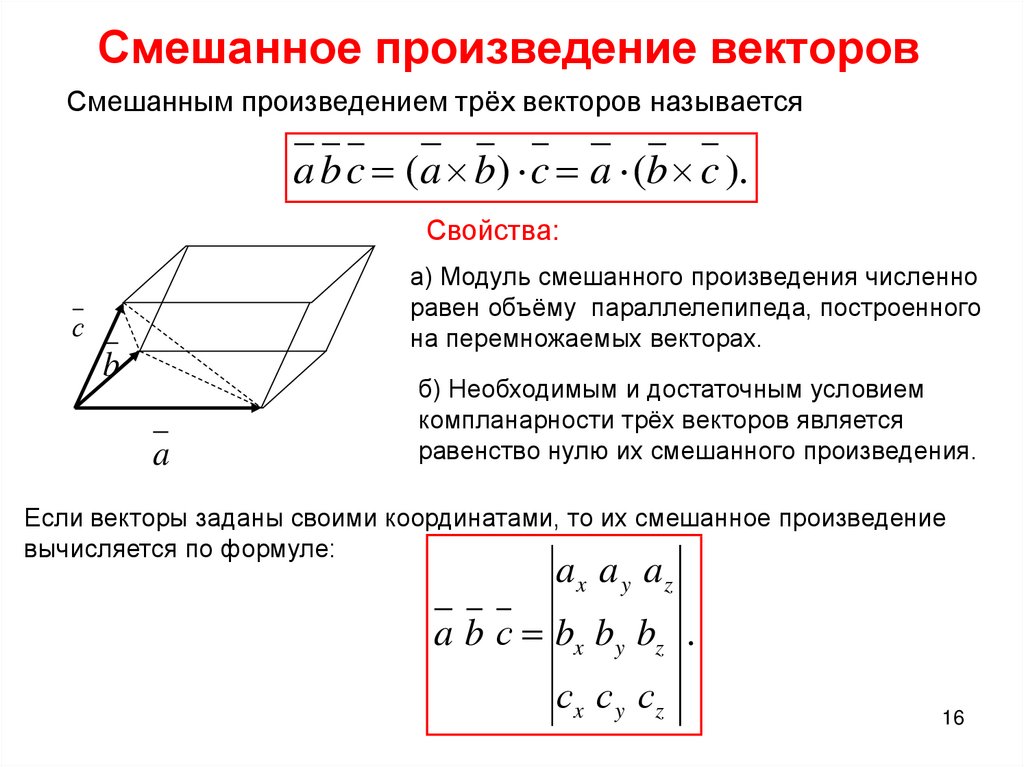
Смешанным произведением трёх векторов называют число, равное . Обозначается . Здесь первые два вектора умножаются векторно и затем полученный вектор умножается скалярно на третий вектор . Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

1. Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т. е. .

   Таким образом, и .

   Доказательство. Отложим векторы от общего начала и построим на них параллелепипед. Обозначим и заметим, что . По определению скалярного произведения

   . Предполагая, что и обозначив через h высоту параллелепипеда, находим .

   Таким образом, при

   Если же , то и . Следовательно, .

   Объединяя оба эти случая, получаем или .

   Из доказательства этого свойства в частности следует, что если тройка векторов правая, то смешанное произведение , а если – левая, то .

2. Для любых векторов , , справедливо равенство

   .

   Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что и . Причём знаки «+» и «–» берутся одновременно, т.к. углы между векторами и и и одновременно острые или тупые.

3. При перестановке любых двух сомножителей смешанное произведение меняет знак.

   Действительно, если рассмотрим смешанное произведение , то, например, или

   .

4. Смешанное произведение тогда и только тогда, когда один из сомножителей равен нулю или векторы – компланарны.

   Доказательство.

   1. Предположим, что , т.е. , тогда или или .

      Если , то или или . Поэтому – компланарны.

      Если , то , , — компланарны.

   2. Пусть векторы – компланарны и α – плоскость, которой они параллельны , т. е. и . Тогда , а значит , поэтому или .

   Т.о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора образуют базис в пространстве, если .

   Если векторы заданы в координатной форме , то можно показать, что их смешанное произведение находится по формуле:

   .

   Т. о., смешанное произведение равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.

   Примеры.

   1. Показать, что векторы образуют базис в пространстве.

      , т.е. векторы – базис.

   2. Найти объём пирамиды с вершинами в точках A(2; -2; 0), B(-1; 4; -4), C(4; -8; 5), D(1; -7; 0). Правую или левую тройку образуют векторы и ?

      Т. к. , то тройка векторов левая.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Уравнение F(x, y, z) = 0 определяет в пространстве Oxyz некоторую поверхность, т.е. геометрическое место точек, координаты которых x, y, z удовлетворяют этому уравнению. Это уравнение называется уравнением поверхности, а x, y, z – текущими координатами.

Однако, часто поверхность задаётся не уравнением, а как множество точек пространства, обладающих тем или иным свойством. В этом случае требуется найти уравнение поверхности, исходя из её геометрических свойств.

ПЛОСКОСТЬ.

НОРМАЛЬНЫЙ ВЕКТОР ПЛОСКОСТИ.

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ

Рассмотрим в пространстве произвольную плоскостьσ. Её положение определяется заданием вектора , перпендикулярного этой плоскости, и некоторой фиксированной точки M₀(x₀, y₀, z₀), лежащей в плоскости σ.

Вектор перпендикулярный плоскости σ, называется нормальным вектором этой плоскости. Пусть вектор имеет координаты .

Выведем уравнение плоскости σ, проходящей через данную точку M₀ и имеющей нормальный вектор . Для этого возьмём на плоскости σ произвольную точку M(x, y, z) и рассмотрим вектор .

Для любой точки MÎ σ вектор .Поэтому их скалярное произведение равно нулю . Это равенство – условие того, что точка MÎ σ. Оно справедливо для всех точек этой плоскости и нарушается, как только точка M окажется вне плоскости σ.

Если обозначить через радиус-вектор точки M, – радиус-вектор точкиM₀, то и уравнение можно записать в виде

.

Это уравнение называется векторным уравнением плоскости. Запишем его в координатной форме. Так как , то

.

Итак, мы получили уравнение плоскости, проходящей через данную точку. Таким образом, для того чтобы составить уравнение плоскости, нужно знать координаты нормального вектора и координаты некоторой точки, лежащей на плоскости.

Заметим, что уравнение плоскости является уравнением 1-ой степени относительно текущих координат x, y и z.

Примеры.

1. Составить уравнение плоскости, проходящей через точку М(1;-2;3) перпендикулярно вектору .

   Используя выведенное уравнение, получим 2(x-1)+0(y+2)+4(z-3)=0 или x+2z-7=0.

2. Составить уравнение плоскости, проходящей через точки A(1;2;3), B(-1;0;0), C(3;0;1).

   Чтобы составить требуемое уравнение, нужно найти вектор перпендикулярный плоскости. Заметим, что таким вектором будет вектор . Найдем это вектор. . Тогда

   .

   Взяв в качестве точки, через которую проходит плоскость точку A, получим уравнение –2(x-1)-10(y-2)+8(z-3)=0 или x+5y-4z+1=0.

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ

Можно показать, что любое уравнение первой степени относительно декартовых координат x, y, z представляет собой уравнение некоторой плоскости. Это уравнение записывается в виде:

Ax+By+Cz+D=0

и называется общим уравнением плоскости, причём координаты A, B, C здесь являются координатами нормального вектора плоскости.

Рассмотрим частные случаи общего уравнения. Выясним, как располагается плоскость относительно системы координат, если один или несколько коэффициентов уравнения обращаются в ноль.

1. Свободный член равен нулю D= 0.

   В этом случае уравнение плоскости принимает вид Ax+Cy+Bz=0. Т.к. числа x=0, y=0, z=0 удовлетворяют уравнению плоскости, то она проходит через начало координат.

2. Один из коэффициентов при текущих координатах равен нулю. Пусть например A =0. В этом случае уравнение плоскости имеет вид By+Cz+D=0. Нормальный вектор плоскости имеет координаты и перпендикулярен оси Ox. Следовательно, плоскость параллельна оси Ox.

   Аналогично, если B= 0, то плоскость параллельна оси Oy и C= 0 – плоскость параллельна оси Oz.

   Т.о., если в уравнении плоскости один из коэффициентов при текущей координате равен нулю, то плоскость параллельна соответствующей координатной оси.

3. Коэффициент при текущей координате и свободный член равны нулю. Например, A = D = 0. В этом случае уравнению By + Cz = 0 соответствует плоскость, проходящая через начало координат (согласно п.1). Кроме того, учитывая п.2, данная плоскость должна быть параллельна оси Ox. Следовательно, плоскость проходит через ось Ox.

   Аналогично, при B=D=0 плоскость Ax+Cz=0 проходит через ось Oy. При C=D=0 плоскость проходит через ось Oz.

4. Два коэффициента при текущих координатах раны нулю. Пусть, например, A=B=0. Тогда плоскость Cz+D=0 в силу п.2 будет параллельна осям Ox и Oy, а следовательно параллельна координатной плоскости xOy.
   Аналогично, уравнениям Ax+D=0 и By+D=0 соответствуют плоскости, параллельные координатным плоскостям yOz и xOz.
5. Два коэффициента при текущих координатах и свободный член равны нулю. Пусть, например, A=B=D=0. Тогда уравнение плоскости имеет вид Cz=0 или z=0. Эта плоскость проходит через начало координат и параллельна осям Ox и Oy, т. е. уравнение определяет координатнуюплоскость xOy. Аналогично, x=0 – уравнение координатной плоскости yOz и y=0 – плоскость xOz.

Примеры.

1. Составить уравнение плоскости, проходящей параллельно оси Oy, через точки M₁(1; 0; -1), M₂(-1; 2;0).

   Так как ось Oy параллельна , то уравнение плоскости Ax+Cy+D=0. Учитывая, что M₁Î α, M₂Î α, подставим координаты этих точек в уравнение и получим систему из двух линейных уравнений с тремя неизвестными

   Положив D=1, найдем A= 1 и C= 2. Следовательно, уравнение плоскости имеет видx+2z+1=0.

2. Составить уравнение плоскости, проходящей через точку M(2;3;-4) параллельно плоскости yOz (перпендикулярно оси Ox).

   Так как yOz||α, то уравнениеплоскости будет Ax+D=0. С другой стороны MÎ α, поэтому 2A+D=0, D=-2A. Поэтому плоскость имеет уравнениеx-2=0.

УРАВНЕНИЕ ПЛОСКОСТИ В ОТРЕЗКАХ.

ПОСТРОЕНИЕ ПЛОСКОСТЕЙ

Рассмотрим плоскость, пересекающую все три координатные оси и не проходящую через начало координат. Пусть плоскость задана своим общим уравнением Ax+By+Cz+D=0, где ни один из коэффициентов не равен нулю.

Преобразуем это уравнение.

Ax+By+Cz=-D. Поделим полученное равенство на –D и запишем его в виде:

.

Тогда, обозначив , приходим к уравнению . Это уравнение и называется уравнением плоскости в отрезках.

Выясним геометрический смысл чисел a, b и c. Если положим y=z=0, то изуравнения x=a. Т.е. данному уравнению удовлетворяет точка с координатами (0; 0; 0). Следовательно, a – это длина отрезка, отсекаемого плоскостью на оси Ox. Аналогично, можно показать, что b и c – длины отрезков, отсекаемых рассматриваемой плоскостью на осях Oy и Oz.

Уравнением плоскости в отрезках удобно пользоваться для построения плоскостей.

Примеры.

1. Построить плоскость 2x+3y+6z-6=0. Приведём это уравнение к уравнению плоскости в отрезках: .

2. 2x—y-4z-4=0. Рассмотрим еще один способ построения плоскостей. Для построения плоскости достаточно найти три какие-либо её точки, не лежащие на одной прямой. Удобнее всего определять точки пересечения плоскости с осями координат.

3. 2x+5z-10=0. Плоскость параллельна оси Oy. Найдём точки пересечения с осями Ox и Oz.
4. Плоскость 3x+2y=0 проходит через ось Oz.
5. 2z+5=0, z=-5/2.

Значение, формула, примеры и уравнение

Знаете ли вы, что Великая пирамида в Гизе имеет высоту около 146,7 м и длину основания 230,6 м? Вы представляете, сколько кубов сахара размером 1 м ³ понадобилось бы, чтобы заполнить Великую пирамиду Гизы? Здесь вы узнаете, как это можно рассчитать, зная объем пирамид.

Что такое пирамида?

Пирамиды представляют собой трехмерные объекты с треугольными сторонами или поверхностями, которые сходятся на вершине, называемой вершиной. Название «пирамида» часто напоминает египетские пирамиды, одно из семи чудес света.

В геометрии пирамида представляет собой многогранник, полученный при соединении многоугольного основания с точкой, называемой вершиной .

Типы пирамид

Пирамиды бывают различных типов в зависимости от формы их основания. Пирамида с треугольным основанием называется треугольной пирамидой , , а пирамида с прямоугольным основанием известна как прямоугольная пирамида . Стороны пирамиды треугольные и выходят из ее основания. Все они встречаются в точке, называемой вершиной.

Изображение, показывающее различные типы пирамид, Нджоку — StudySmarter Originals

Каков объем пирамиды?

Вам может быть интересно, сколько блоков песка может составить египетские пирамиды. Объем пирамиды – это пространство, ограниченное ее гранями. Как правило, объем пирамиды составляет треть соответствующей призмы. Соответствующая ему призма имеет такую ​​же форму основания, размеры основания и высоту. Таким образом, общая формула для расчета объема пирамиды:

V=13×bh ​​

где,

V – объем пирамиды

b – площадь основания пирамиды

h – высота пирамиды

Обратите внимание, что это общая формула для объема все пирамиды. Различия в формулах основаны на форме основания пирамиды.

Объем прямоугольных пирамид

Объем прямоугольных пирамид можно найти, умножив треть площади прямоугольного основания на высоту пирамиды. Следовательно:

Объем прямоугольной пирамиды=13×Площадь основания×высотаПлощадь основания=длина×ширинаОбъем=13×Д×Ш×В

где;

l — длина основания

b — ширина основания

h — высота пирамиды

Иллюстрация сторон прямоугольной пирамиды, Нджоку — StudySmarter Originals

прямоугольной пирамиды составляет треть соответствующей прямоугольной призмы.

Объем пирамид с квадратным основанием

Пирамида с квадратным основанием — это пирамида, основание которой — квадрат. Объем пирамиды с квадратным основанием можно получить, умножив одну треть площади квадратного основания на высоту пирамиды. Следовательно:

Объем квадратного основанияпирамиды=13×Площадь основания×высотаПлощадь основания=длина3Объем=13×l2×h

где;

l — длина квадратного основания

h — высота пирамиды

Иллюстрация сторон пирамиды с квадратным основанием, Нджоку — StudySmarter Originals

Объем пирамид с треугольным основанием

Объем пирамид с треугольным основанием можно получить, умножив одну треть площади треугольного основания на высоту пирамиды. Следовательно:

Объемтреугольнойоснованияпирамиды=13×Площадьоснования×высотаОснованиеплощадь=12×длинаоснования×высотатреугольникаОбъем=13×12×b×hтреугольник×hпирамидаV=16×b×hтреугольник×hпирамида

где;

l – длина основания

b – длина треугольного основания

h _{треугольник} высота треугольного основания

h _{пирамида} высота пирамиды

Иллюстрация сторон треугольной пирамиды, Нджоку — StudySmarter Originals Базовые пирамиды можно получить, умножив одну треть площади шестиугольного основания на высоту пирамиды. Следовательно:

Объем треугольной основанияпирамиды=13×Площадь основания×высотаПлощадь основания=332×длина3Объем=13×332×l2×hОбъем=32×l2×h

Иллюстрация сторон шестиугольной пирамиды, Нджоку — StudySmarter Originals

Пирамида высотой 15 футов имеет квадратное основание 12 футов. Определите объем пирамиды.

Solution

Volumeofsquarebasepyramid=13×l2×hl=12fth=15ftV=13×122×15V=5×144V=720ft3

Calculate the volume of the figure below:

Solution

Thevolumeofthefigure =volumeofrectangularpyramid+volumeofrectangularprismVolumeofrectanglarpyramid=13×l×b×hl=45cmb=20cmh=50cmVolumeofrectanglarpyramid=13×45×20×50Volumeofrectanglarpyramid=15000cm3Volumeofrectangularprism=l×b×hl=45cmb=20cmh=40cmVolumeofrectangularprism=45×20×40Volumeofrectangularprism=36000cm3Thevolumeofthefigure=volumeofrectangularpyramid +объем прямоугольной призмыОбъем фигуры=15000+36000Объем фигуры=51000см3

Шестиугольная пирамида и треугольная пирамида имеют одинаковую емкость. Если его треугольное основание имеет длину 6 см и высоту 10 см, вычислите длину каждой стороны шестиугольника, когда обе пирамиды имеют одинаковую высоту.

Решение

Первым шагом является выражение отношения в уравнении.

Согласно задаче объем треугольной пирамиды равен объему шестиугольной пирамиды.

Лет б _т обозначает площадь основания треугольного основания, а b _h обозначает площадь основания шестиугольного основания.

Тогда:

Объем треугольной пирамиды=Объем шестиугольной пирамидыbth4=bhh4

Умножьте обе части уравнения на 3 и разделите на h.

bth4=bhh4bth4×3h=bhh4×3hbt=bh

Это означает, что треугольное основание и шестиугольное основание имеют одинаковую площадь.

Напомним, что от нас требуется найти длину каждой стороны шестиугольника.

bt=12×длина основания×высотадлина основаниятреугольника=6смвысотатреугольника=10смh=332×l2

Где l — длина стороны шестиугольника.

Напомним, что b _t = b _h , тогда;

12×6×10=332×l212×6×10×233=332×l2×233203=l2

Возьмите корни обеих частей уравнения.

l2=11,547l=3,398 см

Таким образом, каждая сторона шестиугольного основания составляет примерно 3,4 см.

Объем пирамиды — основные выводы

• Пирамида — это трехмерный объект с треугольными сторонами или поверхностями, которые встречаются на вершине, называемой вершиной
• Различные типы пирамид основаны на форме их основания
• Объем пирамиды равен одной трети площади основания × высоты

Как найти объем квадратной пирамиды?

Квадратная пирамида представляет собой трехмерную геометрическую форму с квадратным основанием и четырьмя треугольными сторонами, соединенными в вершине. Он имеет пять сторон и называется многогранником или, точнее, пятигранником. Треугольные стороны пирамиды называются ее гранями, а точка, лежащая над ее основанием, называется вершиной. Всего у него 8 ребер, 5 вершин и 4 грани. Она становится прямоугольной пирамидой, если вершина лежит перпендикулярно центру квадрата. Равносторонняя квадратная пирамида образуется, если все длины ребер равны.

 

Формула объема квадратной пирамиды

Объем квадратной пирамиды определяется как пространство, заключенное между ее пятью гранями. Для расчета объема необходимы значения площади основания и высоты квадратной пирамиды. Его формула равна произведению площади основания и высоты на 3. Стандартная единица измерения – кубические метры (м ³ ).

V = 1/3 × A × h

где

V – объем,

A – площадь основания,

h — высота квадратной пирамиды.

С точки зрения длины основания и высоты квадратной пирамиды, формула для объема определяется следующим образом: ,

a — длина основания,

h — высота квадратной пирамиды.

Как найти объем квадратной пирамиды?

Давайте рассмотрим пример, чтобы понять, как мы можем рассчитать объем квадратной пирамиды.

Пример: Рассчитайте объем квадратной пирамиды с площадью основания 90 кв. м и высотой 5 м.

Шаг 1: Обратите внимание на площадь основания и высоту квадратной пирамиды. В этом примере площадь основания пирамиды составляет 90 кв. м, а высота — 5 м.

Шаг 2: Мы знаем, что объем квадратной пирамиды равен 1/3 × A × h. Подставьте в формулу заданные значения площади основания и высоты.

Шаг 3: Итак, объем треугольной призмы рассчитывается как V = 1/3 × 90 × 5 = 150 куб. м.

Примеры задач

Задача 1. Вычислите объем квадратной пирамиды с площадью основания 60 кв. м и высотой 10 м.

Решение:

Имеем,

A = 60

h = 10

Используя формулу получаем, × 10

= 200 куб. м

Задача 2. Вычислить объем квадратной пирамиды с площадью основания 150 кв. м и высотой 20 м.

Решение:

Мы имеем,

A = 150

H = 20

Используем формулу, которую мы получаем,

В = 1/3 × a × h

= 1/3 × 150 × 20

= 1000 куб. м

Задача 3. Вычислить площадь основания квадратной пирамиды, если ее объем 300 куб. м, а высота 10 м.

Решение:

Имеем,

V = 300

h = 10

Используя формулу получаем,

V = 1/3 × A × h

=> A = 3 В/ч

=> A = 3 (300)/10

=> A = 90 кв. м

Задача 4. Вычислить площадь основания квадратной пирамиды, если ее объем 120 куб. м, а высота 5 м.

Решение:

Имеем,

V = 120

h = 5

Используя формулу получаем, h

=> A = 3 (120)/5

=> A = 72 кв. м

Задача 5.