Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его . .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
.. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
Решено
В математическом тесте школьникам предлагалось 30 задач. За каждый верный ответ начислялось 7 баллов, а за каждый неверный — снималось 3 балла. Костя
В математическом тесте школьникам предлагалось 20 задач. За каждый верный ответ начислялось 5 баллов, а за каждый неверный — снималось 2 балла. Костя получил 65.
Найдите количество различных вариантов раскраски сторон правильного семиугольника в пять цветов (каждая сторона целиком красится в какой-то цвет;
Решено
Листая старый календарь, Вася обнаружил, что в каком-то из месяцев сразу три вторника попали на четные даты. Какой день недели будет в 12-й день
Пользуйтесь нашим приложением
4.4. Объемы и поверхности тел вращения
I. Объемы тел вращения.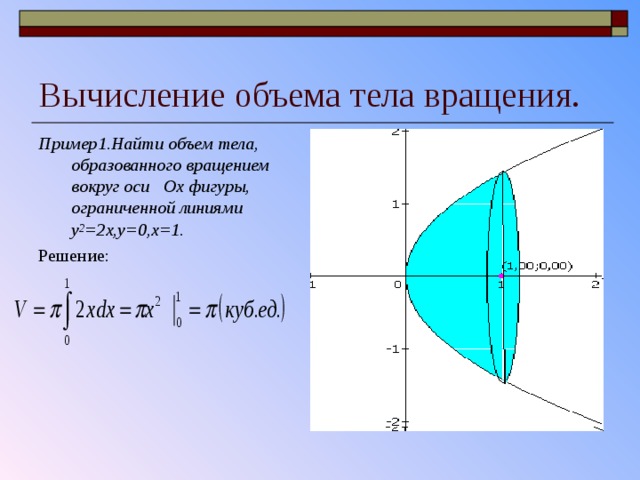 Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п°п° 197, 198* Разберите подробно примеры, приведенные в п° 198.
Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п°п° 197, 198* Разберите подробно примеры, приведенные в п° 198.
508. Вычислить объем тела, образуемого вращением эллипсаВокруг оси Ох.
Решение. При вращении эллипса вокруг оси Ox образуется тело, называемое эллипсоидом вращении. Как известно, объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху кривой у = f{x), ординатами х = а, х = Ь и осью Ох, вычисляется по формуле:
Из уравнения эллипса видно, что большая его полуось равна 2, следовательно,. Разрешив уравнение
эллипса относительно, получимОбъем
эллипсоида вращения равен:
509. Найти объем тора, образованного вращением круга
Вокруг оси Ox (рис. 18). Решение. Искомый объем тора равен разности объемов, полученных от вращения верхнего и нижнего полукругов. Так как для верхнего полукруга
, а для нижнего, то
(см. задачу 388).
Б10. Вычислить объем прямого конуса, высота которого h и радиус основания г, рассматривая конус как тело вращения прямоугольного треугольника около одного из катетов.
Решение. Выберем систему координат так, чтобы ось Ox совпала с высотой h (рис. 19), а вершину конуса
примем за начало координат. Тогда уравнение прямой OA
Следовательно, объем конуса
запишется так: будет равен:
511. Вычислить объемы тел, образованных вращением около осей Ox и Oy сегмента AOB параболы, от
секаемого хордой AFB, проходящей через фокус параболы перпендикулярно к оси Ox (рис. 20, а, б).
Решение I. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Ох, пользуясь формулой:
Найдем пределы интегрирования. Прямая AB параллельна оси Oy. Ее уравнение. Для того чтобы
найти точки пересечения этой прямой с параболой, решим совместно систему уравнений:
мя я AB проходит через фокус параболы, то координаты точки F будутСледовательно,
Получим точки. Так Kaw пря
2. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Oy. Учитывая симметрию сегмента относительно оси Oxi найдем сначала половину искомого объема. Она равна разности объемов тел, получаемых от вращения вокруг оси Oy прямоугольника OFBD и криволинейного тоеугольника OBD. Так как объем цилиндра равен, а объемТела, полученного от вращения криволинейного треугольника OBD вокруг оси Oy, будет:
Она равна разности объемов тел, получаемых от вращения вокруг оси Oy прямоугольника OFBD и криволинейного тоеугольника OBD. Так как объем цилиндра равен, а объемТела, полученного от вращения криволинейного треугольника OBD вокруг оси Oy, будет:
512. Фигура, ограниченная гиперболойИ
то половина искомого объема равна:
Следовательно, весь искомый объем
прямыми, вращается вокруг оси
Ох. Найти объем тела вращения.
Решение. В результате вращения данной фигуры вокруг оси Ox образуются два тела вращения, имеющие равные объемыТогда
Найдем объем V1 тела (рис. 21), сбразованного вращением площади, ограниченной правей ветвью гиперболы И прямейПределы интегрирова
ния найдем из геометрических соображений:
. Таким образом,
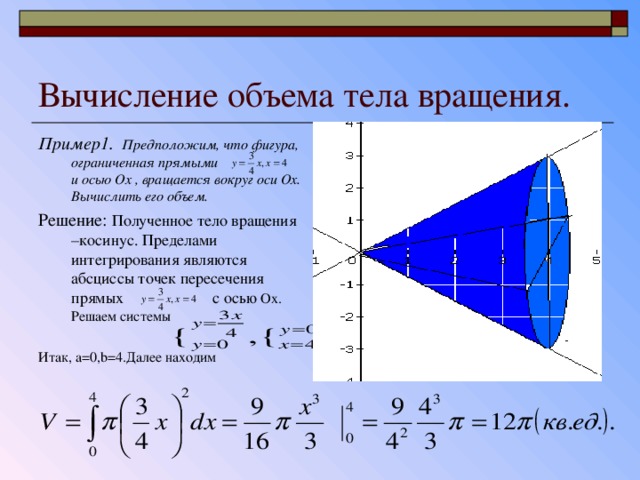
513. Вычислить объем тела, образованного вращением вокруг оси Ox одной полуволны синусоиды у = sin х.
514. Найти объем конуса, производимого вращением вокруг оси Ox части прямой _, содержащейся между осями координат.
515. Криволинейная трапеция, ограниченная срерху параболой,с боков—ординатами х = — I и х—\, снизу — осью Ох, вращается вокруг оси Ох. Найти объем полученного тела вращения.
516. Вычислить объем тела, образованного вращением вокруг оси Ox площади, ограниченной цепной линией
, ординатами X = — а, х = а и осью Ох.
517. Прямой параболический сегмент, основание которого а, а высота R, вращается вокруг основания. Определить объем полученного тела вращения.
518. Найти объем цирка, осевое сечение которого — парабола. Высота цирка 30 м. Диаметр основания 50 м.
519. Найти объем тела, образованного вращением кривойВокруг оси абсцисс.
520. Вычислить объем тела, полученного вращением
астроидыВокруг оси Oy.
521. На кривойВзяты две точки А и В, абсциссы которых соответственно а = I и Ь = 2. Найти объем тела, полученного вращением криволинейной трапеции аАВЬ вокруг оси Ох.
522. Найти объем тела, производимого вращением площади, ограниченной дугой циклоиды,
И осью Ox вокруг ее основания.
523. Вычислить объем тела, образованного вращением вокруг оси ординат дуги OM циклоиды,
, ограниченной точками О (0, 0) и M (та*, 2а).
524. Найти объем тела, ограниченного поверхностью, полученной при вращении линии
вокруг оси абсцисс.
2. Площадь поверхности тела вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 205. В теоретическом курсе показано, что площадь поверхности тела вращения определяется по формуле:
52$. Определить площадь поверхности параболоида, образованного вращением дуги параболы у2 = 2х вокруг оси Ox от х = 0 до х = 2.
Решение. В нашем случае . Поэтому
526. Найти площадь поверхности шара радиуса R. Решение. Поместим начало координат в центре шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружностиВокруг оси Ох. Тогда площадь поверхности шара найдется по формуле:
T ак как
И, следовательно,
527. Найти площадь поверхности эллипсоида, образованного вращением эллипсаВокруг оси Ох.
Найти площадь поверхности эллипсоида, образованного вращением эллипсаВокруг оси Ох.
Решение. Из уравнения эллипса имеем:
. Найдем производную:
Тогда. Так как полуось эллипса
И, следовательно,
Если кривая задана параметрически, то, заменяя переменную под знаком определенного интеграла, получим для площади поверхности следующую формулу:
528 Вычислить площадь поверхности, сбразованной вращением одной арки циклоиды
Вокруг оси Ox (см. рис. 13).
Решение. Найдем:
Тогда. Искомая по
верхность равна:
Решение. Построим данную кривую. Найдем точки пересечения ее с осями координат.
нием петли кривой х = /2, у
(/2— 3) вокруг оси Ох.
При у — 0 находим t = 0 и t = ±}/ 3 . Следовательно, X1 = 0 и X2 -= 3* т. е. кривая пересекает ось Ox в двух точках О (0, 0) и А (3, 0).
При х = 0 находим / = 0, следовательно, у = 0. Мы получили ту же точку О (0, 0).
При люб dx вещественных значениях параметра / будут вещественны х и у Так как х — четная функция параметра /, у — нечетная функция параметра /, то график расположен симметрично относительно оси Ох. з
з
3 Ik 2 2 2 /
530. Найти площадь поверхности, образованной вращением вокруг оси Ox дуги синусоиды у = sin х от точки X = 0 до точки X = It.
531. Вычислить площадь поверхности конуса с высотой h и радиусом г.
532. Вычислить площадь поверхности, образованной
2_ 2_ 2_
вращением астроиды х3 -)- у* — а3 вокруг оси Ох.
533. Вычислить площадь поверхности, образованной цращением петли кривой 18 уг — х (6 — х)г вокруг оси Ох.
534. Найти поверхность тора, производимого вращением круга X2 — j — (у—З)2 = 4 вокруг оси Ох.
535. Вычислить площадь поверхности, образованной вращением окружности X = a cost, y = asint вокруг оси Ох.
536. Вычислить площадь поверхности, образованной вращением петли кривой х = 9t2, у = St — 9t3 вокруг оси Ох.
537. Найти площадь поверхности, образованной вращением дуги кривой х = е*sint, у = el cost вокруг оси Ox
от t = 0 до t = —.
2
538. Показать, что поверхность, производимая вращением дуги циклоиды х = a (q> —sin ф), у = а (I — cos ф) вокруг оси Oy, равна 16 и2 о2.
Показать, что поверхность, производимая вращением дуги циклоиды х = a (q> —sin ф), у = а (I — cos ф) вокруг оси Oy, равна 16 и2 о2.
539. Найти поверхность, полученную вращением кардиоидыВокруг полярной оси.
540. Найти площадь поверхности, образованной вращением лемнискатыВокруг полярной оси.
Дополнительные задачи к главе IV
Площади плоских фигур
541. Найтивсю площадь области, ограниченной кривойИ осью Ох.
542. Найти площадь области, ограниченной кривой
И осью Ох.
543. Найти часть площади области, расположенной в первом квадранте и ограниченной кривой
л осями координат.
544. Найти площадь области, содержащейся внутри
петли:
545. Найти площадь области, ограниченной одной петлей кривой:
546. Найти площадь области, содержащейся внутри петли:
547. Найти площадь области, ограниченной кривой
И осью Ох.
548. Найти площадь области, ограниченной кривой
И осью Ох.
549. Найти площадь области, ограниченной осью Oxr
прямойИ кривой
550. Найти площадь области, ограниченной кривыми.
Найти площадь области, ограниченной кривыми.
И осью Oy.
Вычисление длины дуги
551. Найти длину дуги кривойОт точки А(0: до точки В (I: 6).
552. Найти длину дуги CD кривой, где
Дать геометрическую иллюстрацию.
553. Найти длину дуги OA кривойГде
554. Найти длину дуги AB кривой у = еху где А (0; I), В (I; 2)
555. Нгйти длину дуги AB кривой, где
556. Нгйти длину дуги кривой, отсеченной прямей X = — I.
557. Нгйти длину дуги кривойОт
До
Объем тела вращения
558. Нгйти объем тела, полученного вращением вокруг юси Ox п/ощоди, сграниченной крквой
559. Нййти объем тела, полученного от вращения рокруг сси Ox площади, ограниченной кривой
560. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченной кривой
ц прямыми
561. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченней эллипсом
562. Нгйти объем тела, полученного вращением вокруг оси Oy плещади, ограниченной кривой
И отрезком оси Oy.
563. Найти объем тела, полученного вращением вокруг оси Ox площади, ограниченной кривой
564. Круг радиуса 2 с центром в точке (7; 0) вращается вокруг оси Oy. Определить объем полученного тела вращения.
565. Нлйти объем тела, полученного вращением вокруг оси Ox площади, расположенной в первом квадранте и
ограниченной кривой(эволюта
эллипса).
Площадь поверхности вращения
566. Найти площадь поверхности, образованной вращением дуги кривой, отсеченной прямой
567. Найти площадь поверхности шаоовой чаши, полученной при вращении кругаВокруг оси Ox в пределах от 0 до h.
568. Найти площадь поверхности катеноида, образованного вращением вокруг оси абсцисс цепной линии
От точкиДо точки
569. Найти площадь поверхности эллипсоида, образованного вращением эллипсаВокруг оси Oy.
570. Найти площадь поверхности, образованной вращением вокруг оси Ox петли кривой
571. Найти площадь поверхности, образованной вращением вокруг оси Ox кривой
572. Найти площадь поверхности, образованной вращениемВокруг полярной оси.
Найти площадь поверхности, образованной вращениемВокруг полярной оси.
ПРИЛОЖЕНИЯ К ВОПРОСАМ ФИЗИКИ
| < Предыдущая | Следующая > |
|---|
6.3: Объемы революции — цилиндрические оболочки
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2521
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Вычислить объем тела вращения, используя метод цилиндрических оболочек.
- Сравните различные методы расчета объема вращения.
В этом разделе мы рассмотрим метод цилиндрических оболочек, последний метод нахождения объема тела вращения. Мы можем использовать этот метод для тех же типов твердых тел, что и метод диска или метод шайбы; однако при использовании метода диска и шайбы мы интегрируем по оси координат, параллельной оси вращения. Методом цилиндрических оболочек интегрируем по координате ось перпендикулярна оси вращения. Возможность выбирать, какую переменную интегрирования мы хотим использовать, может быть значительным преимуществом для более сложных функций. Кроме того, специфическая геометрия твердого тела иногда делает метод использования цилиндрических оболочек более привлекательным, чем метод шайбы. В последней части этого раздела мы рассмотрим все методы определения объема, которые мы изучили, и изложим некоторые рекомендации, которые помогут вам определить, какой метод использовать в той или иной ситуации.
Мы можем использовать этот метод для тех же типов твердых тел, что и метод диска или метод шайбы; однако при использовании метода диска и шайбы мы интегрируем по оси координат, параллельной оси вращения. Методом цилиндрических оболочек интегрируем по координате ось перпендикулярна оси вращения. Возможность выбирать, какую переменную интегрирования мы хотим использовать, может быть значительным преимуществом для более сложных функций. Кроме того, специфическая геометрия твердого тела иногда делает метод использования цилиндрических оболочек более привлекательным, чем метод шайбы. В последней части этого раздела мы рассмотрим все методы определения объема, которые мы изучили, и изложим некоторые рекомендации, которые помогут вам определить, какой метод использовать в той или иной ситуации.
Метод цилиндрических оболочек
Опять же, мы работаем с телом вращения. Как и прежде, определим область \(R\), ограниченную сверху графиком функции \(y=f(x)\), снизу \(x\)-осью , а слева и справа от линий \(x=a\) и \(x=b\) соответственно, как показано на рисунке \(\PageIndex{1a}\). Затем мы вращаем эту область вокруг оси \(y\), как показано на рисунке \(\PageIndex{1b}\). Обратите внимание, что это отличается от того, что мы делали раньше. Ранее области, определяемые в терминах функций \(x\), вращались вокруг 9∗_i)\) и ширину \(Δx\). Репрезентативный прямоугольник показан на рисунке \(\PageIndex{2a}\). Когда этот прямоугольник вращается вокруг оси \(y\), вместо диска или шайбы мы получаем цилиндрическую оболочку, как показано на рисунке \(\PageIndex{2}\).
Затем мы вращаем эту область вокруг оси \(y\), как показано на рисунке \(\PageIndex{1b}\). Обратите внимание, что это отличается от того, что мы делали раньше. Ранее области, определяемые в терминах функций \(x\), вращались вокруг 9∗_i)\) и ширину \(Δx\). Репрезентативный прямоугольник показан на рисунке \(\PageIndex{2a}\). Когда этот прямоугольник вращается вокруг оси \(y\), вместо диска или шайбы мы получаем цилиндрическую оболочку, как показано на рисунке \(\PageIndex{2}\).
Другой способ представить это — сделать вертикальный надрез в оболочке, а затем открыть ее, чтобы сформировать плоскую пластину (рис. \(\PageIndex{4}\)).
Рисунок \(\PageIndex{4}\): (a) Сделайте вертикальный разрез в репрезентативной оболочке. ∗_i\) и толщиной \(Δx\) (рисунок). Таким образом, объем оболочки примерно равен объему плоской пластины. Умножая высоту, ширину и глубину тарелки, получаем 9.b_a(2π\,x\,f(x))\,dx. \nonumber \]
∗_i\) и толщиной \(Δx\) (рисунок). Таким образом, объем оболочки примерно равен объему плоской пластины. Умножая высоту, ширину и глубину тарелки, получаем 9.b_a(2π\,x\,f(x))\,dx. \nonumber \]Это приводит к следующему правилу для метода цилиндрических оболочек .
Правило: метод цилиндрических оболочек
Пусть \(f(x)\) непрерывна и неотрицательна. Определим \(R\) как область, ограниченную сверху графиком \(f(x)\), снизу осью \(x\), слева линией \(x=a\) , а справа линией \(x=b\). Тогда объем тела вращения, образованного вращением \(R\) вокруг оси \(y\), равен 9b_a(2π\,x\,f(x))\,dx. \nonumber \]
Теперь рассмотрим пример.
Пример \(\PageIndex{1}\): Метод цилиндрических оболочек I
Определить \(R\) как область, ограниченную сверху графиком \(f(x)=1/x\) и снизу по оси \(x\) на интервале \([1,3]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг оси \(y\).
Решение
Сначала мы должны построить область \(R\) и связанное с ней тело вращения, как показано на рисунке \(\PageIndex{5}\). 93\)
93\)
Как и в случае метода диска и метода шайбы, мы можем использовать метод цилиндрических оболочек с телами вращения, вращающимися вокруг оси \(x\), когда мы хотим проинтегрировать по \(y\). Аналогичное правило для этого типа твердого тела приведено здесь.
Правило: Метод цилиндрических оболочек для тел вращения вокруг оси \(x\)
Пусть \(g(y)\) непрерывна и неотрицательна. Определим \(Q\) как область, ограниченную справа графиком \(g(y)\), слева — осью \(y\), снизу линией \(y=c\) , а выше строкой \(y=d\). Тогда объем тела вращения, образованного вращением \(Q\) вокруг оси \(x\), равен 9d_c(2π\,y\,g(y))\,dy. \nonumber \]
Пример \(\PageIndex{3}\): Метод цилиндрических оболочек для твердого тела, вращающегося вокруг оси \(x\)
Определить \(Q\) как область, ограниченную справа по графику \(g(y)=2\sqrt{y}\) и слева по оси \(y\) для \(y∈[0,4]\). Найдите объем тела вращения, образованного вращением \(Q\) вокруг оси \(х\).
Решение
Во-первых, нам нужно изобразить область \(Q\) и связанное с ней тело вращения, как показано на рисунке \(\PageIndex{7}\). 93 \end{align*}\]
93 \end{align*}\]
Упражнение \(\PageIndex{3}\)
Определить \(Q\) как область, ограниченную справа графиком \(g(y)=3/y \) и слева по оси \(y\) для \(y∈[1,3]\). Найдите объем тела вращения, образованного вращением \(Q\) вокруг оси \(х\).
- Подсказка
Используйте процесс из примера \(\PageIndex{3}\).
- Ответить
\(12π\) единиц 9*_i)\left(\dfrac {x_i+x_{i-1}}{2}\right)(x_i-x_{i-1}).\end{align*}\]
Это было основано на оболочка с внешним радиусом \(x_i\) и внутренним радиусом \(x_{i−1}\). Однако если мы повернем область вокруг линии, отличной от оси \(y\), мы получим другой внешний и внутренний радиусы. Предположим, например, что мы вращаем область вокруг линии \(x=−k,\), где \(k\) — некоторая положительная константа. Тогда внешний радиус оболочки равен \(x_i+k\), а внутренний радиус оболочки равен \(x_{i−1}+k\). Подставляя эти члены в выражение для объема, мы видим, что при вращении плоской области вокруг линии \(x=−k,\) объем оболочки равен 9b_a(2π(x+k)f(x))dx.
 \nonumber \]
\nonumber \]Мы также можем вращать область вокруг других горизонтальных или вертикальных линий, таких как вертикальная линия в правой полуплоскости. В каждом случае формула объема должна быть скорректирована соответствующим образом. В частности, член \(х\) в интеграле должен быть заменен выражением, представляющим радиус оболочки. Чтобы увидеть, как это работает, рассмотрим следующий пример.
Пример \(\PageIndex{4}\): область вращения, вращающаяся вокруг линии
Определим \(R\) как область, ограниченную сверху графиком \(f(x)=x\) и снизу по оси \(x\) на интервале \([1,2]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг линии \(x=−1.\)
Решение
Сначала начертите область \(R\) и связанное с ней тело оборот, как показано на рисунке \(\PageIndex{8}\).
Рисунок \(\PageIndex{8}\): (a) Область \(R\) между графиком \(f(x)\) и осью \(x\) на интервале \([1 ,2]\). (b) Тело вращения, образованное вращением \(R\) вокруг линии \(x=−1. \) 92\) и ниже по оси \(x\) на интервале \([0,1]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг линии \(x=−2\).
\) 92\) и ниже по оси \(x\) на интервале \([0,1]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг линии \(x=−2\).- Подсказка
Используйте процесс из примера \(\PageIndex{4}\).
- Ответить
\(\dfrac {11π}{6}\) единиц 3
В качестве последнего примера в этом разделе рассмотрим объем тела вращения, область вращения которого ограничена графиками двух функций.
Пример \(\PageIndex{5}\): область вращения, ограниченная графиками двух функций
Определим \(R\) как область, ограниченную сверху графиком функции \(f(x)= \sqrt{x}\) и ниже по графику функции \(g(x)=1/x\) на интервале \([1,4]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг оси \(y\).
Решение
Сначала начертите область \(R\) и соответствующее тело вращения, как показано на рисунке \(\PageIndex{9}\).
Рисунок \(\PageIndex{9}\): (a) Область \(R\) между графиком \(f(x)\) и графиком \(g(x)\) на интервале \ ([1,4]\). (b) Тело вращения, образованное вращением \(R\) вокруг оси \(y\).
Обратите внимание, что осью вращения является ось \(y\), поэтому радиус оболочки задается просто \(x\). Нам не нужно вносить какие-либо коррективы в x-член нашего подынтегрального выражения. Однако высота оболочки определяется выражением \(f(x)−g(x)\), поэтому в этом случае нам нужно скорректировать член \(f(x)\) подынтегральной функции. Тогда объем твердого тела равен 92\) на интервале \([0,1]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг оси \(y\).
- Подсказка
Подсказка: используйте процесс из примера \(\PageIndex{5}\).
- Ответить
\(\dfrac {π}{6}\) единиц 3
Какой метод следует использовать?
Мы изучили несколько методов нахождения объема тела вращения, но как узнать, какой метод использовать? Часто все сводится к выбору того, какой интеграл проще всего вычислить.
Рисунок \(\PageIndex{10}\) Рисунок \(\PageIndex{10}\) описывает различные подходы для тел вращения вокруг оси \(x\). Вам предстоит разработать аналогичную таблицу для тел вращения вокруг оси \(y\).
Рисунок \(\PageIndex{10}\) описывает различные подходы для тел вращения вокруг оси \(x\). Вам предстоит разработать аналогичную таблицу для тел вращения вокруг оси \(y\).Давайте рассмотрим пару дополнительных задач и выберем наилучший подход к их решению.
Пример \(\PageIndex{6}\): выбор наилучшего метода
Для каждой из следующих задач выберите наилучший метод нахождения объема тела вращения, образованного вращением заданной области вокруг \(x \)-ось и настройте интеграл, чтобы найти объем (интеграл не оценивайте).
- Область, ограниченная графиками \(y=x, y=2−x,\) и осью \(x\). 92\) и оси \(х\).
Раствор
а.
Сначала нарисуйте область и тело вращения, как показано.
Рисунок \(\PageIndex{11}\): (a) Область \(R\), ограниченная двумя линиями и осью \(x\). (b) Тело вращения, образованное вращением \(R\) вокруг оси \(x\).Глядя на область, если мы хотим интегрировать по \(x\), нам придется разбить интеграл на две части, потому что у нас есть разные функции, ограничивающие область по \([0,1]\) и \([1,2]\).
 В этом случае, используя дисковый метод, мы получили бы 91_0 2π\,y[2−2y]\,dy. \nonumber \]
В этом случае, используя дисковый метод, мы получили бы 91_0 2π\,y[2−2y]\,dy. \nonumber \]Ни один из этих интегралов не является особенно обременительным, но поскольку метод оболочки требует только одного интеграла, а подынтегральная функция требует меньшего упрощения, в данном случае нам, вероятно, следует использовать метод оболочки.
б.
Сначала нарисуйте область и тело вращения, как показано.
Рисунок \(\PageIndex{12}\): (a) Область \(R\) между кривой и осью \(x\). (b) Тело вращения, образованное вращением \(R\) вокруг оси \(x\). 92\справа]\,dx\номер\]
Ключевые понятия
- Метод цилиндрических оболочек — еще один метод использования определенного интеграла для вычисления объема тела вращения. Этот метод иногда предпочтительнее либо метода дисков, либо метода шайб, потому что мы интегрируем по другой переменной. В некоторых случаях один интеграл существенно сложнее другого.
- Геометрия функций и сложность интегрирования являются основными факторами при принятии решения о том, какой метод интегрирования использовать.
 9b_a\left(2π\,x\,f(x)\right)\,dx\)
9b_a\left(2π\,x\,f(x)\right)\,dx\)Глоссарий
- метод цилиндрических оболочек
- метод расчета объема тела вращения путем деления тела на вложенные друг в друга цилиндрические оболочки; этот метод отличается от методов дисков или шайб тем, что мы интегрируем по противоположной переменной
Эта страница под названием 6.3: Volumes of Revolution — цилиндрические оболочки распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент. это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- метод цилиндрических оболочек
- тело вращения
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 - Объем по Shells
Объяснение урока: Объемы тел вращения
В этом объяснении мы узнаем, как найти объем сгенерированного твердого тела путем вращения области вокруг горизонтальной или вертикальной линии с помощью интеграция.
Предположим, у нас есть кривая 𝑦=𝑓(𝑥) в некотором интервале [𝑎,𝑏], как показано на диаграмме.
Если мы возьмем часть кривой между 𝑥=𝑎 и 𝑥=𝑏 и повернем ее вокруг оси 𝑥 на полный оборот (т.е. на 360∘ или 2𝜋), кривая отобразит поверхность твердого тела как он вращался; это называется телом вращения, как показано на диаграмме.
Если бы кривая, определяемая 𝑓, описывала бы прямую линию, мы бы получили конус. Если бы он описывал круг, мы бы получили сферу. Так как же определить объем таких тел вращения?
Определение: Объем тел вращения
Предположим, что между вертикальными линиями 𝑥=𝑎 и 𝑥=𝑏 лежит твердое тело, площадь поперечного сечения которого в плоскости, проходящей через 𝑥 и перпендикулярной оси 𝑥, равна 𝐴(𝑥).
 Если 𝐴(𝑥) непрерывно на интервале [𝑎,𝑏], мы можем разделить интервал на 𝑛 подынтервалов одинаковой ширины, Δ𝑥, и выбрать точку, 𝑥, в каждом интервале.
Если 𝐴(𝑥) непрерывно на интервале [𝑎,𝑏], мы можем разделить интервал на 𝑛 подынтервалов одинаковой ширины, Δ𝑥, и выбрать точку, 𝑥, в каждом интервале.Объем твердого тела, образованного вращением области, ограниченной кривой и осью 𝑥 между 𝑥=𝑎 и 𝑥=𝑏 вокруг оси 𝑥, определяется выражением 𝑉=𝐴(𝑥)Δ𝑥=𝐴(𝑥)𝑥,limd→∞ куда 𝑥=𝑎+𝑖Δ𝑥,Δ𝑥=𝑏−𝑎𝑛=𝑥−𝑥.
Аналогично, объем твердого тела, образованного вращением области, ограниченной кривой и осью 𝑦 между 𝑦=𝑐 и 𝑦=𝑑 вокруг оси 𝑦, определяется выражением 𝑉=𝐴(𝑦)𝑦.d
Это также можно изобразить на диаграмме.
Для кривой 𝑦=𝑓(𝑥) форма поперечного сечения представляет собой сплошной диск или круг, площадь которого равна 𝐴=𝜋𝑅, где 𝑅 — радиус. Радиус каждого круга будет значением функции в этой точке. Таким образом, поперечное сечение, перпендикулярное оси вращения, представляет собой диск радиуса 𝑅=𝑓(𝑥), и мы имеем 𝐴(𝑥)=𝜋[𝑓(𝑥)].
Следовательно, объем твердого тела, образованного вращением области, ограниченной кривой 𝑦=𝑓(𝑥) и осью 𝑥 между 𝑥=𝑎 и 𝑥=𝑏, вокруг оси 𝑥, можно альтернативно записать как 𝑉=𝜋[𝑓(𝑥)]𝑥.
 d
dМы можем визуализировать это на графике следующим образом:
Мы также можем использовать аналогичный процесс для вычисления объема твердого тела, вращающегося вокруг оси 𝑦 . Объем твердого тела, образованного вращением области, ограниченной кривой 𝑥=𝑓(𝑦) и осью 𝑦 между 𝑦=𝑐 и 𝑦=𝑑, вокруг оси 𝑦 определяется выражением 𝑉=𝜋[𝑓(𝑦)]𝑦.d
Это можно представить следующим образом:
В качестве примера выведем формулы для объема сферы. Уравнение окружности с центром в начале координат и радиусом 𝑟 задается как 𝑥+𝑦=𝑟 или, что то же самое, записывается как функция от 𝑥 как 𝑦=±√𝑟−𝑥.
Фактически, нам нужно только рассмотреть полуокружность в верхнем полуквадранте, описанную 𝑦=√𝑟−𝑥, как показано на графике:
Мы можем вращать эту кривую между 𝑥=−𝑟 и 𝑥=𝑟 вокруг этой оси 𝑥 на полный оборот, чтобы сформировать сферу радиуса 𝑟 с центром в начале координат.
Площадь поперечного сечения этого твердого тела определяется выражением 𝐴(𝑥)=𝜋𝑦=𝜋𝑟−𝑥.

Следовательно, объем тела вращения равен 𝑉 = 𝐴 (𝑥) 𝑥 = 𝜋𝑟 — 𝑥𝑥 = 𝜋𝑟𝑥 — 𝑥3 = 𝜋𝑟 — 𝑟3 — — 𝑟+𝑟3 = 43𝜋𝑟. dd
Это стандартный результат для объема сферы, как и ожидалось. Мы получили бы тот же результат, если бы рассмотрели полуокружность в области ниже оси 𝑥, описываемую 𝑦=−√𝑟−𝑥.
Теперь давайте проделаем то же самое для объема конуса. Рассмотрим уравнение прямой линии, проходящей через начало координат, 𝑦=𝑟ℎ𝑥, как показано на графике.
Мы можем повернуть эту линию между 𝑥=0 и 𝑥=ℎ, сделав полный оборот вокруг оси 𝑥, чтобы сформировать конус радиуса 𝑟 и высоты по вертикали ℎ, как показано на диаграмме.
Площадь поперечного сечения этого твердого тела определяется выражением 𝐴(𝑥)=𝜋𝑦=𝜋𝑟ℎ𝑥=𝜋𝑟ℎ𝑥.
Следовательно, объем тела вращения определяется выражением 𝑉 = 𝐴 (𝑥) 𝑥 = 𝜋𝑟ℎ𝑥𝑥 = 𝜋𝑟ℎ𝑥𝑥 = 𝜋𝑟ℎ𝑥3 = 𝜋𝑟ℎℎ3−0 = 13𝜋𝑟ℎ. ddd
Это стандартный результат для объема конуса, как и ожидалось.

Теперь давайте рассмотрим несколько примеров, чтобы попрактиковаться и углубить наше понимание как вычислить объемы тел вращения с помощью интегрирования. В первом примере определим объем твердого тела порожденные полной революцией того или иного региона относительно 𝑥-ось. Это будет определено с помощью интегрирования.
Пример 1. Нахождение объема твердого тела, образованного вращением области, ограниченной заданной линией вокруг оси 𝑥
Рассмотрим область, ограниченную кривыми 𝑦=𝑥+4, 𝑦=0, 𝑥=0 и 𝑥=3. Определите объем тела вращения, созданного вращением этой области вокруг оси 𝑥.
Ответ
В этом примере мы хотим вычислить объем твердого тела, образованного вращением определенной области вокруг оси 𝑥.
Мы можем визуализировать область, ограниченную кривыми 𝑦=𝑥+4, 𝑦=0, 𝑥=0 и 𝑥=3, следующим образом:
Тело вращения, образованное вращением этой области вокруг оси 𝑥, представляет собой усеченный конус, имеющий вид обрезанного на конце конуса.

Поскольку мы вращали область вокруг оси 𝑥, объем определяется выражением 𝑉=𝐴(𝑥)𝑥.d
Форма вертикального поперечного сечения нашего тела будет диском, а радиус 𝑅 каждого диска будет значением функции в этой точке, 𝑅= 𝑥+4. Таким образом, площадь поперечного сечения определяется выражением 𝐴(𝑥)=𝜋𝑅=𝜋(𝑥+4).
Пределы интеграла 𝑎 и 𝑏 определяются вертикальными границами 𝑥 в области, ограниченной кривыми 0≤𝑥≤3; это также можно визуализировать из графика области, ограниченной кривыми. Таким образом, имеем 𝑎=0 и 𝑏=3, а объем тела вращения определяется выражением 𝑉=𝐴(𝑥)𝑥=𝜋(𝑥+4)𝑥=𝜋𝑥+8𝑥+16𝑥=𝜋𝑥3+8𝑥2+16𝑥=93𝜋.ddd
Таким образом, объем тела вращения равен 93𝜋.кубических единиц
В следующем примере мы определим объем, создаваемый оборотом области, ограниченной радикальной функцией и другими прямыми, о 𝑥-ось. Это будет определено с помощью интегрирования.
Пример 2. Нахождение объема тела, образованного вращением области под кривой корневой функции относительно оси 𝑥
Найдите объем тела, полученного вращением области, ограниченной кривой 𝑦=√ 𝑥+1 и линии 𝑦=0 и 𝑥=4 относительно оси 𝑥.

Ответ
В этом примере мы хотим вычислить объем твердого тела, образованного вращением определенной области вокруг оси 𝑥.
Мы можем визуализировать область, ограниченную кривой 𝑦=√𝑥+1 и линиями 𝑦=0 и 𝑥=4, следующим образом:
Тело вращения, образованное вращением этой области вокруг оси 𝑥, выглядит следующим образом:
Поскольку мы вращаем эту область вокруг оси 𝑥, объем определяется выражением 𝑉=𝐴(𝑥)𝑥.d
Форма вертикального поперечного сечения нашего тела будет диском, а радиус каждого диска будет значением функции в этой точке, 𝑅=√𝑥+ 1. Таким образом, площадь поперечного сечения определяется выражением 𝐴(𝑥)=𝜋𝑅=𝜋√𝑥+1=𝜋(𝑥+1).
Пределы интеграла 𝑎 и 𝑏 определяются вертикальными границами 𝑥 в области. Верхняя граница равна 𝑥=4, а нижняя граница определяется пересечением кривых 𝑦=√𝑥+1 и 𝑦=0, что равно 𝑥=−1; это также можно визуализировать из графика области, ограниченной кривыми. Таким образом, имеем 𝑎=−1 и 𝑏=4, а объем тела вращения определяется выражением 𝑉=𝐴(𝑥)𝑥=𝜋(𝑥+1)𝑥=𝜋𝑥2+𝑥=25𝜋2.
 dd
dd25𝜋2.кубических единиц
Теперь давайте рассмотрим пример, где нам нужно найти объем твердое тело, порожденное вращением области, ограниченной параболой вокруг 𝑥-ось. Это будет определено с помощью интегрирования.
Пример 3. Нахождение объема тела, образованного вращением области, ограниченной параболой, вокруг оси 𝑥
Найдите объем тела, образованного вращением области, ограниченной кривой 𝑦=−𝑥+2𝑥 и ось 𝑥 совершают полный оборот вокруг оси 𝑥.
Ответ
В этом примере мы хотим вычислить объем твердого тела, образованного вращением определенной области вокруг оси 𝑥.
Мы можем представить область, ограниченную кривой 𝑦=−𝑥+2𝑥 и осью 𝑥, следующим образом:
Тело вращения, образованное вращением этой области вокруг оси 𝑥, выглядит следующим образом:
Поскольку мы вращают эту область вокруг оси 𝑥, объем определяется выражением 𝑉=𝐴(𝑥)𝑥.d
Форма поперечного сечения нашего тела будет диском, а радиус каждого диска будет значением функции в этой точке, 𝑅=−𝑥+2𝑥 .
 Таким образом, площадь поперечного сечения определяется выражением
𝐴(𝑥)=𝜋𝑅=𝜋−𝑥+2𝑥=𝜋𝑥−4𝑥+4𝑥.
Таким образом, площадь поперечного сечения определяется выражением
𝐴(𝑥)=𝜋𝑅=𝜋−𝑥+2𝑥=𝜋𝑥−4𝑥+4𝑥.Пределы интеграла 𝑎 и 𝑏 определяются вертикальными границами 𝑥 в области, которая в данном случае возникает, когда кривая 𝑦=−𝑥+2𝑥 пересекает ось 𝑥 или когда 𝑦=0: −𝑥+2𝑥=−𝑥(𝑥−2)=0,
Решения задаются формулами 𝑥=0 и 𝑥=2, которые также можно визуализировать из графика области, ограниченной кривыми. Таким образом, имеем 𝑎=0 и 𝑏=2, а объем тела вращения определяется выражением Таким образом, генерируемого твердого тела 16𝜋15.кубических единиц
Теперь давайте рассмотрим пример, в котором мы определяем объем твердого тела. вращения, но на этот раз вращался вокруг оси 𝑦. Этот будет определяться с помощью интегрирования.
Пример 4. Нахождение объема твердого тела, образованного вращением области, ограниченной заданными линиями, вокруг оси 𝑦
Найдите объем тела, образованного путем полного оборота вокруг оси 𝑦, область, ограниченная кривой 9𝑥−𝑦=0 и линиями 𝑥=0, 𝑦=−9и 𝑦=0.

Ответ
В этом примере мы хотим рассчитать объем твердого тела, образованного вращением определенной области вокруг оси 𝑦.
Мы можем визуализировать область, ограниченную кривыми 9𝑥−𝑦=0 и линиями 𝑥=0, 𝑦=−9 и 𝑦=0, следующим образом:
Тело вращения, образованное вращением этой области вокруг 𝑦- ось имеет вид конуса.
Поскольку мы вращали эту область вокруг оси 𝑦, объем определяется выражением 𝑉=𝐴(𝑦)𝑦.d
Форма горизонтального поперечного сечения нашего твердого тела будет диском, а радиус каждого диска будет значением функции в этой точке, 𝑅=𝑦9. Таким образом, площадь поперечного сечения определяется выражением 𝐴(𝑦)=𝜋𝑅=𝜋𝑦9=𝜋𝑦81.
Пределы интеграла 𝑐 и 𝑑 определяются горизонтальными границами 𝑦 в области −9≤𝑦≤0; это также можно визуализировать из графика области, ограниченной кривыми. Таким образом, имеем 𝑐=−9 и 𝑑=0, а объем тела вращения определяется выражением 𝑉=𝐴(𝑦)𝑦=𝜋81𝑦𝑦=𝜋81𝑦3=3𝜋.dd
Таким образом, объем образовавшегося твердого тела равен 3𝜋.
 cubicunits
cubicunitsОбъем 𝑉 твердого тела, образованного вращением области, ограниченной 𝑦=𝑓(𝑥) и 𝑦=𝑔(𝑥) на интервале [𝑎,𝑏], где 𝑓(𝑥)≥𝑔(𝑥) , относительно оси 𝑥 𝑉=𝜋[𝑓(𝑥)]−[𝑔(𝑥)]𝑥,d который мы также можем изобразить на диаграмме:
Аналогично, объем 𝑉 твердого тела, образованного вращением области, ограниченной 𝑥=𝑓(𝑦) и 𝑥=𝑔(𝑦) на интервале [𝑐,𝑑], где 𝑓 (𝑦)≥𝑔(𝑦), относительно оси 𝑦 𝑉=𝜋[𝑓(𝑦)]−[𝑔(𝑦)]𝑥,d что можно представить как:
Теперь давайте рассмотрим несколько примеров о кривых двух функций, вращающихся вокруг оси, где форма поперечного сечения каждого сгенерированного твердого тела представляет собой диск.
Мы начнем с определения объема твердого тела, образованного вращением вокруг оси 𝑦 области, ограниченной двумя функциями от 𝑦, парой многочленов степени 2 и 4.
Пример 5. Нахождение объема твердого тела, образованного вращением области, ограниченной параболой, и кривой степенной функции относительно оси 𝑦
Найдите объем тела, полученного вращением области, ограниченной кривыми 𝑥=6−5𝑦 и 𝑥=𝑦, вокруг оси 𝑦.

Ответ
В этом примере мы хотим рассчитать объем твердого тела, образованного вращением определенного область вокруг оси 𝑦.
Область, ограниченную кривыми 𝑥=6−5𝑦 и 𝑥=𝑦, можно представить следующим образом:
Тело вращения, образованное вращением 𝑥=6−5𝑦 вокруг оси 𝑦, выглядит так:
А тело, образованное 𝑥=𝑦, выглядит так:
Таким образом, тело вращения, образованное вращением области, ограниченной этими кривыми, вокруг оси 𝑦, выглядит так:
Поскольку мы вращали эту область вокруг 𝑦 -ось, объем определяется выражением 𝑉=𝐴(𝑦)𝑦.d
Форма поперечного сечения каждого тела будет кольцом, а радиус каждого диска будет значением функции в этой точке, 𝑅=6−5𝑦 и 𝑟=𝑦. Таким образом, разница между площадями большего и меньшего дисков определяется выражением 𝐴(𝑦)=𝜋𝑅−𝜋𝑟=𝜋6−5𝑦−𝜋𝑦=𝜋36−60𝑦+25𝑦−𝑦.
Пределы интеграла 𝑐 и 𝑑 определяются горизонтальными границами 𝑦 в области, которая в данном случае задается значениями 𝑦 в точках пересечения двух кривых: 6−5𝑦=𝑦.

Решение дается формулой 𝑦=1 и 𝑦=−1, и две кривые пересекаются в точках (1,−1) и (1,1); это также можно визуализировать из графика области, ограниченной кривыми. Таким образом, имеем 𝑐=−1 и 𝑑=1, а объем тела вращения определяется выражением 𝑉=𝐴(𝑦)𝑦=𝜋36−60𝑦+25𝑦−𝑦𝑦=𝜋36𝑦−20𝑦+5𝑦−𝑦9=376𝜋9.дд
Таким образом, объем образовавшегося твердого тела равен 376𝜋9.cubicunits
Теперь давайте рассмотрим пример, где нам нужно найти объем твердое тело, порожденное вращением области, ограниченной двумя кривыми, a парабола и линия вокруг оси 𝑦. Это будет определяется с помощью интегрирования.
Пример 6. Нахождение объема твердого тела, образованного вращением области, ограниченной параболой и линией вокруг оси 𝑦
Найдите объем твердого тела, полученного вращением области, ограниченной кривой 𝑦=𝑥 и линией 𝑥=3𝑦, вокруг оси 𝑦.
Ответ
В этом примере мы хотим вычислить объем твердого тела, образованного вращением определенной области вокруг оси 𝑦.

Мы можем визуализировать область, ограниченную кривой 𝑥=𝑦 и линией 𝑥=3𝑦, следующим образом:
Тело вращения, образованное вращением 𝑥=𝑦 вокруг оси 𝑦, выглядит следующим образом:
А тело, образованное 𝑥=3𝑦, выглядит так:
Таким образом, тело вращения, образованное вращением области, ограниченной этими кривыми, вокруг оси 𝑦, выглядит так:
Поскольку мы вращали область вокруг 𝑦- оси, объем определяется выражением 𝑉=𝐴(𝑦)𝑦.d
Форма горизонтального поперечного сечения нашего тела будет кольцом, а радиус каждого диска будет значением функции в этой точке, 𝑅=3𝑦 и 𝑟 =𝑦. Таким образом, площадь поперечного сечения определяется выражением 𝐴(𝑦)=𝜋𝑅−𝜋𝑟=𝜋(3𝑦)−𝜋𝑦=𝜋9𝑦−𝑦.
Пределы интеграла 𝑐 и 𝑑 определяются горизонтальными границами 𝑦 в области, которая в данном случае находится в месте пересечения двух кривых: 𝑦=3𝑦.
Решения задаются формулами 𝑦=0 и 𝑦=3, а две кривые пересекаются в точках (0,0) и (9,3); это также можно визуализировать из графика области, ограниченной кривыми.
 Таким образом, имеем 𝑐=0 и 𝑑=3, а объем тела вращения определяется выражением
𝑉=𝐴(𝑦)𝑦=𝜋9𝑦−𝑦𝑦=𝜋3𝑦−𝑦5=162𝜋5.dd
Таким образом, имеем 𝑐=0 и 𝑑=3, а объем тела вращения определяется выражением
𝑉=𝐴(𝑦)𝑦=𝜋9𝑦−𝑦𝑦=𝜋3𝑦−𝑦5=162𝜋5.ddТаким образом, объем образовавшегося твердого тела равен 162𝜋5.cubicunits
Ключевые точки
- Первый метод : Когда кривая одной функции вращается вокруг оси, форма поперечного сечения твердого тела будет диском, а радиус, 𝑅, каждого disk будет значением функции в этой точке. Площадь поперечного сечения определяется по формуле 𝐴=𝜋𝑅.
Объем твердого тела, образованного вращением области, ограниченной кривой 𝑦=𝑓(𝑥) и осью 𝑥 между 𝑥=𝑎 и 𝑥=𝑏, вокруг оси 𝑥 определяется выражением 𝑉=𝜋[𝑓(𝑥)]𝑥.d Точно так же объем твердого тела, образованного вращением области, ограниченной кривой 𝑥=𝑓(𝑦) и осью 𝑦 между 𝑦=𝑐 и 𝑦=𝑑 вокруг оси 𝑦, определяется выражением 𝑉=𝜋[𝑓(𝑦)]𝑦.d - Второй метод : когда кривые двух функций вращаются вокруг оси, форма поперечного сечения каждого сгенерированного тела будет кольцом, а радиусы 𝑅 и 𝑟 будут значением каждой из функции в этот момент.

