Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально определить ее ОДЗ.
Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.
При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю.
Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn . Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Для нахождения области определения произведения функций необходимо применять правило:
Определение 2Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Пример 2Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1является постоянной функцией, f2является арктангенсом, f3– логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞) . Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x)– произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x)является -∞, +∞D(f)=D(f).
Получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x — [0, +∞).
Области определения y=f(x) и y=−f(x)совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Пример 3Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Пример 4Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)).
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Пример 5Найти область определения y=ln x2.
Решение
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Пример 6Найти область определения функции y=(arcsin x)-12.
Решение
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Пример 7Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3– логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1) . Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x)
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Пример 8Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел.
Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3–это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4– это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Область определения логарифма с переменной в основании
Определение 3Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1.
После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Пример 9Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Пример 10Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2имеет вид D(f2)=[−3, 0]∪[3, +∞).
После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
| Функция | Ее область определения |
Сумма, разность, произведение функций f1, f2,…, fn | Пересечение множеств D(f1), D(f2), . |
Сложная функция y=f1(f2(f3(…fn(x))))
В частности, y=f1(f2(x)) | Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1)
x∈D(f2),f2(x)∈D(f1) |
.., D(fn)Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y=k·x | R |
| Линейная y=k·x+b | R |
Обратная пропорциональность y=kx | -∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C — число | D(f) |
Дробная y=f1(x)f2(x)
В частности, если f1(x), f2(x) — многочлены | Множество всех x, которые одновременно удовлетворяют условиям
f2(x)≠0 |
| y=f(x)n, где n — четное | x∈D(f1), f(x)≥0 |
y=logf2(x)f1(x)
В частности, y=logaf1(x)
В частности, y=logf2(x)a | x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1
x∈D(f1), f1(x)>0
x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения.
Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Функции одной переменной и многое другое.
.. Пошаговое решение математических задач7.7 Функции одной переменной
уникальный номер в другом, возможно, другом наборе. Первый набор называется областью определения функции, а второй набор называется диапазоном. Если f обозначает функцию, а a обозначает число в домене, то f(a) обозначает число в диапазоне, который f присваивает a. Число f(a) называется значением f в точке a. Если x — переменная над областью определения f, мы говорим, что f — функция переменной x или просто функция x.
Правило соответствия многих функций определяется алгебраическими выражениями. Например, уравнение
f(x)=2x+3
определяет функцию f. Чтобы использовать это уравнение для нахождения числа, которое f присваивает 4, мы просто заменяем каждое вхождение x на 4. У нас есть
f(4)=2(4)+3
=11
и, таким образом, значение f at 4 равно 11.
Когда функция f определяется уравнением, ее область определения понимается как множество всех действительных чисел, для которых определена правая часть уравнения.
Для приведенной выше функции f, поскольку 2x+3 определено для всех действительных чисел x, областью определения является множество всех действительных чисел.
Пример 1.
Пусть g и h – функции, определяемые формулой g(x)=(x+1)/(x-1) и h(x)=root(x+2) find (a)g (0), (b)g(1/2), (c)h(-1) и (d)h(1/4).
(а) g(0)=(0+1)/(0-1)
=-1
(б) g(1/2)=(1/2+1)/(1/2 -1)
=(3/2)/(-1/2)
=-3
(c) h(-1)=корень((-1)+2)
1
=1
(d) h(1/4)=корень((1/4)+2)
=корень(9/4)
1 93 1=81810 Пример 2.
Найдите области определения функций g и h, определенных в примере 1. Поскольку (x+l)/(x-1) определено для всех x, кроме x=1, областью определения g является набор всех действительных чисел, кроме 1. Выражение root(x+2) определено только тогда, когда x+2 неотрицательно. Мы видим, что x+2 неотрицательно тогда и только тогда, когда x больше или равно -2.
Таким образом, доменом h является множество всех действительных чисел, больших или равных -2.
Под графиком функции f понимается график уравнения
y=f(x)
Таким образом, график функции f, определяемой выражением f(x)=2x+3, является графиком уравнения y=2x+3. Этот график представляет собой прямую линию с наклоном 2 и пересечением Y 3. Чтобы построить график f, мы находим точки на графике, первые координаты которых равны 0 и 2.
= 2 (0) +3
= 3
при x = 2,
y = f (2)
= 2 (2) +3
= 7
Таким2-4
Это парабола с вершиной (0,-4), осью симметрии осью Y и раскрытием вверх.
| х | у=ч(х) |
| -3 | 5 |
| -1 | -3 |
| -2 | 0 |
| 0 | -4 |
| 1 | -3 |
| 2 | 0 |
| 3 | 5 |
Давайте посмотрим, как наш математический решатель строит графики для этой и подобных функций.
Пожалуйста, нажмите «Решить похожее», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
Функция f также может быть определена графиком, а не уравнением. Поскольку точки на графике точно совпадают с координатами (a,f(a)), мы можем найти f(a), измерив направленное расстояние от точки (a,0) по оси X до точки (a, f(a)) на графике.
Пример 4.
Найдите f(3), где функция f представлена на графике ниже.
Для оценки f(3) измеряем направленное расстояние от точки
(3,0) до точки (3,f(3)). Это можно сделать, проведя горизонтальную линию от (3,f(3)) к оси Y и оценив координату Y точки пересечения. Мы видим, что f(3) приблизительно равно -0,8. Мы пишем
f(3)≈-0,8
Где «-0,8» означает «приблизительно равно».1813
Функция иногда определяется уравнением с двумя переменными
Если у нас есть уравнение относительно x и y, которое определяет не более одного значения y для каждого значения x, то мы говорим, что уравнение определяет y как функцию Икс.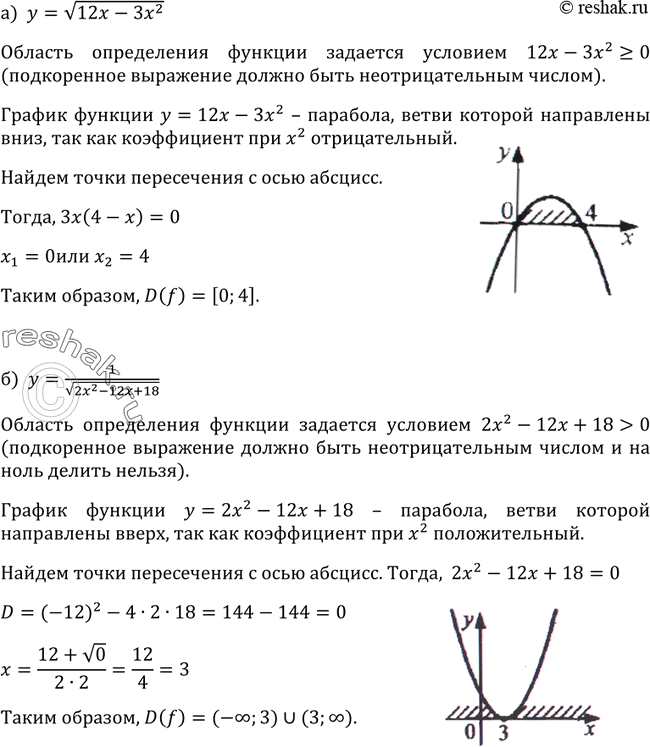
Конечно, не все уравнения относительно x и y определяют y как функцию от x.
Пример 5.
Определяет ли 2x+4y-3=0 y как функцию x?
Решим это уравнение относительно y через x.
2x+4y-3=0
4y=-2x+3
y=-1/2x+3/4
Ясно, что для каждого значения x уравнение действительно определяет уникальное значение y, следовательно, оно определяет y как функцию x.
Рассмотрите график этого уравнения:
2x+4y-3=0
Интерпретируя геометрически условие, что каждый x определяет уникальный y, мы видим, что уравнение определяет y как функцию x, если для каждого значения x вертикальная линия на (x,0) пересекает график не более одного раза. Приведенный выше график, безусловно, обладает этим свойством. 92
Мы видим, что график представляет собой параболу с вершиной (1, 0), осью симметрии — осью X и раскрытием вправо.
| х | г |
| 1 | 0 |
| 2 | +-1 |
Каждая вертикальная линия на (x, 0), где x больше 1, дважды пересекает график.
Это говорит нам геометрически, что это уравнение не определяет у как функцию от х. 92)/((x+1) (x-1))
=-(4/(x+1) (x-1))
7,8 Функции более одной переменной
Иногда это необходимо использовать функцию, область определения которой представляет собой набор пар чисел. Пусть f обозначает такую функцию, а (x, y) – пару переменных над областью определения f. Тогда f(x,y) обозначает значение off в паре (x, y), а f является функцией двух переменных x и y.
Пример 1.
Пусть f определяется уравнением f(x,y)=x+y+xy . Оцените f, когда (x,y) имеет следующие значения: (a)(1,2), (b)(-3,1/2), (c)(a+1,b-3).92-14
Функции одной или нескольких переменных возникают, когда мы решаем уравнение с двумя или более переменными для одной переменной через другие. Полученное уравнение выражает одну переменную как функцию других переменных.
Пример 4.
Рассмотрим xy+x-yz=z Выразите y как функцию x и z.