Обратная матрица. Ранг матрицы — презентация онлайн
Похожие презентации:
Определители матриц. Обратная матрица, ранг матрицы
Матрицы. Элементарные преобразования и действия над матрицами
Обратная матрица
Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения
Матрицы и определители
Матрицы. Свойства операций над матрицами. Теорема о ранге матрицы
Матрицы и определители
Матрицы и их виды. Действия над матрицами. Тема 2
Матрицы. Обозначение матриц
Матрицы и определители
Тема 4. «Обратная матрица. Ранг матрицы.»
Основные понятия:
1. Определение обратной матрицы
2. Способы нахождения обратной матрицы
3. Ранг матрицы, способы нахождения ранга
матрицы
1. Определение обратной матрицы
Необходимо: матрица должна быть квадратной.
A 1 называется обратной по отношению к
матрице А, если A A 1 A 1 A E
Матрица
Теорема. Для невырожденной матрицы А существует
1
A
единственная обратная матрица
 Способы нахождения обратной матрицы
Способы нахождения обратной матрицыАлгоритм нахождения обратной матрицы:
1)
Вычисление определителя матрицы А,
2)
Построение матрицы алгебраических дополнений Aij
(присоединенная матрица)
3)
4)
Нахождение
A
T
ij
Нахождение обратной матрицы
T
1
A Aij
1
Обращение матрицы можно осуществить
по следующему правилу.
1. Вычислить определитель исходной матрицы
Δ = det A.
2. Сформировать матрицу из алгебраических
дополнений всех элементов исходной матрицы
Aij ( 1)i j M ij .
3. Транспонировать матрицу алгебраических
дополнений, что дает присоединенную матрицу
по отношению к исходной матрице A.
4. Каждый элемент присоединенной матрицы
разделить на определитель исходной матрицы Δ.
Пример 1.10. Произвести обращение матрицы
2
4
A
1 4
и доказать, что она обратная.
Решение
1. det A 2 4 1 4 4
2.
3.
4.
4 4
1 2
4 1
4 2
– определитель.

– матрица из алгебраических
дополнений.
– транспонированная матрица
из алгебраических дополнений.
1 4 4
1
1
0.25 0.5
4 1 2
– обратная матрица.
Доказательство: Если A-1 – обратная матрица,
то справедливо выражение AA-1 = E.
2 4
1
1 2 1 4 0.25 2 1 4 0.5 1 0
1 4 0.25 0.5 1 1 4 0.25 1 1 4 0.5 0 1
7. Действия над матрицами
Нахождение обратной матрицыОбратной матрицей по отношению к данной невырожденной
квадратной матрице A n — ного порядка, называется матрица,
которая, будучи умноженной как слева, так и справа на данную
матрицу, дает единичную матрицу.
Обратная матрица обозначается символом А-1. Таким образом,
согласно определению: АА-1=А-1А=Е.
1
A
A A
A det A 0 A
det A
T
1
Транспонированная матрица
Присоединенная матрица
получается из матрицы А Если определитель матрицы
получается путем замены каждого
путем замены строк т
равен нулю, то обратная
элемента матрицы А на его
соответствующими
матрица не существует
алгебраическое дополнение
столбцами
8.
 Действия над матрицами0 3 1
Действия над матрицами0 3 10 3 1
0 3 1
2 1
4
(
1
)
2
2
1
0
det
A
2
4
1
A 2 4 1
2 2
2 2 0
2 2 0
2 2 0
0 2 2 Из второй -2
T
A 2
A 3 4 строки
2 вычтем
строку
1 1 первую
0
-4
2 -1
Разложим
-2 2 определитель
по элементам
3 столбца
6 -6
4 2
A 11 3 2
( 1)2 3 2
2 320 42 3 5
A 12 0
1 20 ( 1) 2
2 23
2 2 ( 4 1( 4) (
A 21 A
)14)2 1
0
A
2
1 0( 1)5 6
1
A
13
0
2
AA
(
1
)
4
1 320.5
11) 1 62 1
12 101 (21
31 22
A
(
1
)
6
3 2
1 4331 2 03 4
1
1
A 2 2
2 1 1
2
2
3
3
4
6
6
Алгоритм нахождения обратной матрицы (Метод Гаусса):
1)
К матрице А справа приписывается Е,
2)
Проделывая преобразования над строками расширенной
матрицей (А|Е), матрицу А приводят к Е,
3)
Справа на месте приписанной матрицы Е будет
получена обратная матрица.

Примеры. Найдем обратные матрицы к матрицам
2 4
,
1 2
1 2 4
0 2 4
3 1 2
10. 3. Ранг матрицы
11. Ранг матрицы (1)
Рассмотрим матрицуa11
a 21
A
….
a
m1
a12
a 22
….
am2
a 1n
…. a 2 n
….. …..
….. a mn
….
Минором к – го порядка матрицы А
называется определитель к – го порядка
с элементами, стоящими на пересечении
любых к строк и к столбцов.
(k min m, n )
12. Ранг матрицы (2)
Рангом матрицы r(A)называется наибольший
из порядков миноров данной
матрицы, отличных от нуля.
13. Элементарные преобразования матриц
Элементарныепреобразования матриц
Вычеркивание
нулевой строки
Прибавление к
одной из строк другой
строки, умноженной
на любое число
Перестановка
двух строк
14. Элементарные преобразования матриц (1)
Теорема 1.Любую матрицу с помощью
элементарных преобразований
можно привести к
ступенчатому виду.

15. Элементарные преобразования матриц (2)
Теорема 2.При элементарных
преобразованиях ранг
матрицы не меняется.
Ранг ступенчатой матрицы равен числу
(ненулевых) строк.
16. Пример 6 (1)
Найти ранг матрицы:1 -3 -1
A= 2 1 4 .
3 -2 3
17. Пример 6 (2)
Решение. Приведем матрицу к ступенчатому виду:1 -3 -1
2 1 4
3 -2 3
·(-2)
↓
←
18. Пример 6 (3)
Решение.1 -3 -1
2 1 4
3 -2 3
·(-2)
↓
←
1 -3 -1
0 7 6
3 -2 3
19. Пример 6 (4)
Решение.1 -3 -1
2 1 4
3 -2 3
·(-2)
↓
←
1 -3 -1
0 7 6
3 -2 3
·(-3)
↓
←
20. Пример 6 (5)
Решение.1 -3 -1
2 1 4
3 -2 3
·(-2)
↓
←
1 -3 -1
0 7 6
3 -2 3
·(-3)
↓
←
1 -3 -1
0 7 6
0 7 6
21. Пример 6 (6)
Решение.1 -3 -1
0
7
6
0 7 6
1 -3 -1
·(-1) 0 7 6
↓
0 0 0
←
22.
 Пример 6 (7) Решение.
Пример 6 (7) Решение.1 -3 -1
0
7
6
0 7 6
1 -3 -1
1 -3 -1
·(-1) 0 7 6
0
7
6
↓
0 0 0
←
r(A)=2
3. Ранг матрицы, способы нахождения ранга матрицы
Рангом матрицы называют наибольший из порядков ее
миноров, отличных от нуля (обозначается r).
Способ нахождения ранга матрицы (по свойству миноров):
Свойство миноров. Если все миноры порядка k данной
матрицы равны нулю, то все миноры более высокого
Следовательно, если среди миноров порядка k данной
матрицы есть отличные от нуля, а все миноры порядка
(k+1) равны нулю или не существуют, ранг матрицы
равен k.
Способ нахождения ранга матрицы (сведение матрицы к
квазитреугольной форме).
Пример. Найти ранг матрицы
6
9
3
0
0 2 1 3
5 7 6 6
,
0 1 2 1
5 4 3 2
r 3
English Русский Правила
Калькулятор сопряженных матриц — MathCracker.com
Инструкции:
Используйте этот калькулятор, чтобы найти сопряженную матрицу, которую вы предоставляете, показывая все шаги. Сначала нажмите на одну из кнопок ниже, чтобы указать размерность матрицы.
Сначала нажмите на одну из кнопок ниже, чтобы указать размерность матрицы.
Затем щелкните первую ячейку и введите значение и перемещайтесь по матрице, нажимая «TAB» или щелкая соответствующие ячейки, чтобы определить ВСЕ значения матрицы.
Так же, как и кофакторы, присоединенная матрица тесно связана с обратной матрицей. Действительно, обратная матрица и присоединенная матрица очень похожи.
Справедливости ради стоит отметить, что понятие сопряжения матрицы играет очень важную роль в высшей математике (где вместо матриц мы имеем дело с линейными операторами). Но в математике в колледже единственный раз, когда вы, вероятно, наткнетесь на сопряженное, это когда вы
вычислить обратную матрицу
используя формулу сопряжения.
Пример расчета сопряженной матрицы
Вопрос: Рассмотрим следующую матрицу
\[ \begin{bmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 4&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{bmatrix}\]
Вычислите соответствующую сопряженную матрицу \(adj A\).
Решение:
Нам нужно вычислить сопряженную матрицу предоставленной матрицы \(3 \times 3\):
Шаг 1: вычислить матрицу кофакторов
Сначала мы вычисляем матрицу миноров. { 3 3} = \begin{vmatrix}
\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 2&\displaystyle 4
\end{vmatrix}
= 2 \cdot \left( 4 \right) — 2 \cdot \left(3 \right) = 2\]
{ 3 3} = \begin{vmatrix}
\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 2&\displaystyle 4
\end{vmatrix}
= 2 \cdot \left( 4 \right) — 2 \cdot \left(3 \right) = 2\]
Подводя итог, матрица несовершеннолетних выглядит следующим образом:
\[M = \begin{bmatrix} \displaystyle 3&\displaystyle 1&\displaystyle -2\\[0.6em]\displaystyle 2&\displaystyle 1&\displaystyle -1\\[0.6em]\displaystyle -1&\displaystyle 0&\displaystyle 2 \end{bmatrix} \]
Теперь мы можем вычислить элементы матрицы кофакторов \(C\), используя формулу
\[ C_{ij} = (-1)^{i+j}M_{ij}\]
Приведенную выше формулу можно использовать напрямую, поскольку миноры уже известны. T = \begin{bmatrix}
\displaystyle 3&\displaystyle -2&\displaystyle 1\\[0.6em]\displaystyle -1&\displaystyle -1&\displaystyle 0\\[0.6em]\displaystyle -2&\displaystyle 1&\displaystyle -2
\end{bmatrix}
\]
T = \begin{bmatrix}
\displaystyle 3&\displaystyle -2&\displaystyle 1\\[0.6em]\displaystyle -1&\displaystyle -1&\displaystyle 0\\[0.6em]\displaystyle -2&\displaystyle 1&\displaystyle -2
\end{bmatrix}
\]
что завершает вычисление сопряженной матрицы.
Калькулятор сопряженных матриц — MathCracker.com
Инструкции: Используйте этот калькулятор, чтобы найти сопряженную матрицу, которую вы предоставляете, показывая все шаги. Сначала нажмите на одну из кнопок ниже, чтобы указать размерность матрицы.
Затем нажмите на первую ячейку и введите значение, и перемещайтесь по матрице, нажимая «TAB» или щелкая соответствующие ячейки, чтобы
определить ВСЕ значения матрицы.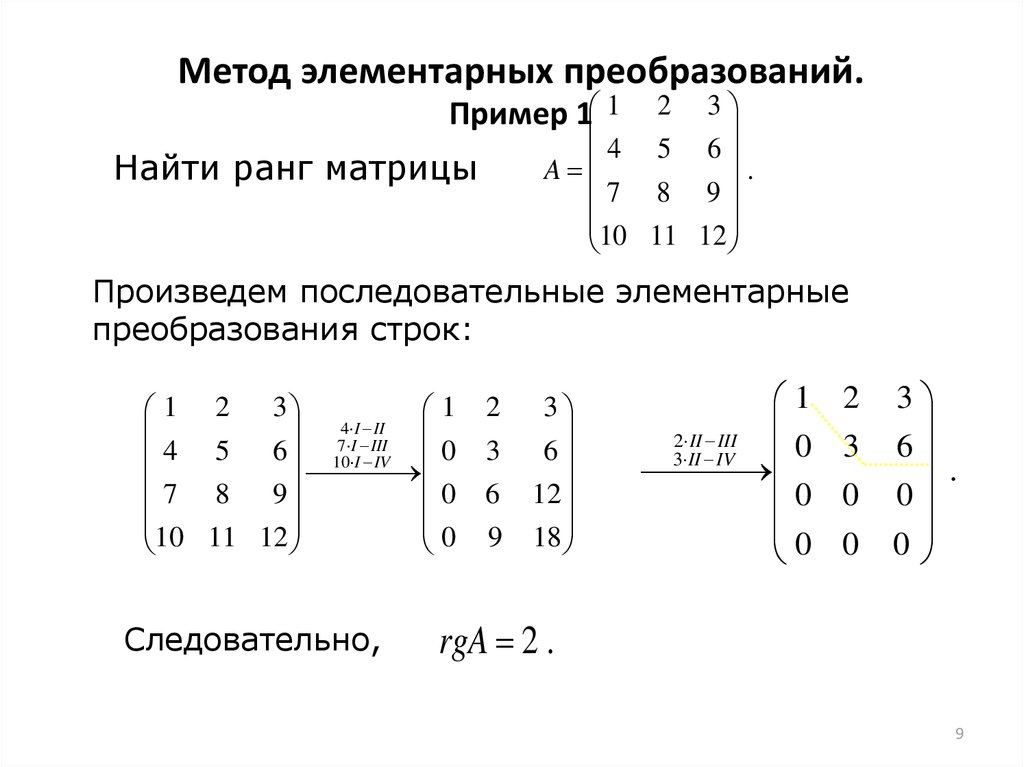
Так же, как и кофакторы, присоединенная матрица тесно связана с обратной матрицей. Действительно, обратная матрица и сопряженная матрицы очень похожи.
Справедливости ради следует отметить, что понятие сопряжения матрицы играет очень важную роль в высшей математике (где вместо матриц мы имеем дело с линейными операторы). Но в математике колледжа единственный раз, когда вы, вероятно, наткнетесь на сопряженное, это когда вы вычисляете обратную матрицу, используя сопряженное формула.
Как найти сопряженную матрицу?
Во-первых, с точки зрения того, как вычисляется сопряженная матрица, давайте вспомним матрицу миноров, которая вычисляется путем вычисления определителя подматриц, образованных удалением i-й строки и j-го столбца заданной
матрица \(А\). {i,j}\]
9{i+j} M_{ij}\]
{i,j}\]
9{i+j} M_{ij}\]
Наконец, как добраться до сопряженной матрицы? Что такое формула сопряжения?
Просто! После того, как вы уже рассчитали матрицу кофакторов, вам нужно транспонировать матрица чтобы получить сопряженное. Конкретно: 9Т \]
Итак, чтобы облегчить запоминание, мы разбили сопряженную формулу на 3 шага: сначала вы вычисляете матрицу миноров, затем вы вычисляете кофакторы, а затем переставляете кофакторы, чтобы получить сопряженное.
Сопряженное и транспонированное одно и то же?
Хотя сопряженная включает транспонирование матрицы, в общем случае сопряженная и транспонированная матрицы отличаются друг от друга. 92\) субдетерминанты, которые могут
быстро расти с \(n \ge 4\).
92\) субдетерминанты, которые могут
быстро расти с \(n \ge 4\).
Пример расчета сопряженной матрицы
Вопрос: Рассмотрим следующую матрицу
\[ \begin{bmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 4&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \конец{bmatrix}\] 9{ 3 3} = \begin{vmatrix} \displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 2&\displaystyle 4 \end{vmatrix} = 2 \cdot \left( 4 \right) — 2 \cdot \left(3 \right) = 2\]
Подводя итоги, матрица миноров:
\[M = \begin{bmatrix} \displaystyle 3&\displaystyle 1&\displaystyle -2\\[0.6em]\displaystyle 2&\displaystyle 1&\displaystyle -1\\[0.6em]\displaystyle -1&\displaystyle 0&\displaystyle 2 \end{bmatrix} \] 9{ 6} \cdot 2 = -2\]
Подводя итог, матрица кофакторов:
\[C = \begin{bmatrix}
\displaystyle 3&\displaystyle -1&\displaystyle -2\\[0. 6em]\displaystyle -2&\displaystyle -1&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 0&\displaystyle -2
\end{bmatrix}
\]
6em]\displaystyle -2&\displaystyle -1&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 0&\displaystyle -2
\end{bmatrix}
\]
Шаг 2: Вычисление сопряженной матрицы из матрицы кофакторов
Теперь нам нужно транспонировать найденную матрицу кофакторов для вычисления сопряженной матрицы. Получаем: 9Т = \begin{bmatrix} \displaystyle 3&\displaystyle -2&\displaystyle 1\\[0.6em]\displaystyle -1&\displaystyle -1&\displaystyle 0\\[0.6em]\displaystyle -2&\displaystyle 1&\displaystyle -2 \end{bmatrix} \]
, что завершает вычисление сопряженной матрицы.
Калькулятор сопряженных матриц (Adjugate Matrix)
Создано Анной Щепанек, доктором философии
Отзыв написан Войцехом Сас, доктором философии, и Джеком Боутером
Последнее обновление: 15 февраля 2022 г.
Содержание:- Что такое сопряженная матрица (сопряженная матрица)?
- Сопряжение матрицы 2×2
- Как использовать этот калькулятор сопряженных матриц?
- Формула сопряженной матрицы для обращения матрицы
- Часто задаваемые вопросы
Добро пожаловать в калькулятор сопряженных матриц Omni! Здесь вы можете быстро и легко определить сопряженную (а. к.а. сопряженную) квадратную матрицу. Не знаете, что такое сопряжение матрицы? Нужно быстро напомнить как найти сопряженную матрицу ? В статье ниже мы научим вас всему, что вам нужно знать о сопряженной/сопряженной матрице! Мы даем формулу сопряженной матрицы и объясняем, как найти по этой формуле сопряженную матрицу размера 2×2.
к.а. сопряженную) квадратную матрицу. Не знаете, что такое сопряжение матрицы? Нужно быстро напомнить как найти сопряженную матрицу ? В статье ниже мы научим вас всему, что вам нужно знать о сопряженной/сопряженной матрице! Мы даем формулу сопряженной матрицы и объясняем, как найти по этой формуле сопряженную матрицу размера 2×2.
Что такое сопряженная матрица (сопряженная матрица)?
Прежде всего, имейте в виду, что то, что мы здесь называем сопряженной матрицей, иногда называют сопряженной матрицей. Вы также можете встретить термин классическая сопряженная матрица. Эта путаница происходит из-за того, что в некоторых контекстах термин , присоединенный к , может означать сопряженное транспонирование матрицы, что полностью отличается от того, что мы здесь рассматриваем. Мы будем свободно смешивать термины примыкающий и прилежащий , чтобы вы могли быстро привыкнуть к ним обоим.
Как найти сопряжение матрицы?
Предположим, A — это n × n -матрица с действительными или комплексными элементами. Чтобы найти адъюгат A , выполните следующие действия:
- Удалите
i-ю строку иj-й столбецA. Вы получаете(n - 1) × (n - 1)подматрицуA. - Вычислите определитель этой подматрицы. То, что вы получите, называется
(i, j)-минор изA. - Умножьте
(i, j)-минор числаAна знаковый коэффициент(-1) i+j. То, что вы получаете, называется(i, j)-кофактор изA. - Повторить шаги 1, 2 и 3 для всех
i,j = 1,...,n. - Сопряженный матрицы
Aпредставляет собой матрицуn × n, запись(i, j)которой является кофактором(j, i)матрицыA. Обратите внимание, индексы перевернуты!
Обратите внимание, индексы перевернуты!
👉 Сопряженная матрица A часто обозначается как adj(A) .
👉 Если вы уже знакомы с понятием матрица кофакторов , то вы, возможно, поняли, что adj(A) на самом деле является транспонированием матрицы кофакторов из A .
Сопряжение матрицы 2×2
Давайте посмотрим, как работает описанная выше формула сопряженной матрицы в простейшем случае. А именно, мы будем использовать его, чтобы найти сопряжение матрицы 2×2. Рассмотрим следующую матрицу:
| ⌈ | a | b | ⌉ |
| ⌊ | c | d | ⌋ |
Коэффициентов четыре, поэтому мы повторим шаги 1, 2 и 3 из предыдущего раздела четыре раза.
Пусть
i=1иj=1.Удаление первой строки и первого столбца оставляет нам матрицу
1 x 1. Его единственный коэффициент равенd. Следовательно, его определитель также равенd. Знаковый фактор равен(-1) 1+1 = 1(1, 1)-кофактор нашей исходной матрицы равенd.Пусть
i=1иj=2.Удаление первой строки и второго столбца оставляет нам матрицу
1 x 1, содержащуюc. Коэффициент знака задается как(-1) 1+2 = -1, поэтому(1, 2)-кофактор нашей исходной матрицы равен-c.Пусть
i=2иj=1.Аналогично, здесь у нас есть матрица
1 x 1, содержащаяb, и коэффициент знака равен(-1) 2+1 = -1, поэтому(2, 1)-кофактор нашей исходной матрицы равно-b.
Пусть
i=2иj=2.Наконец, мы имеем дело с матрицей
1 x 1, содержащейa, коэффициент знака равен(-1) 2+2 = 1, поэтому(2, 2)-кофактор исходной матрицы равенa.
Далее, чтобы найти сопряжение нашей матрицы, подставляем (i, j) -кофактор в j -ю строку и i -й столбец:
-
(1, 1)-кофактор, который равенd, идет в первую строку и первый столбец :
| ⌈ | d | ⌉ | |
| ⌊ | ⌋ |
- The
(1, 2)-cofactor, which is equal to-c, goes to the вторая строка и первый столбец :
| ⌈ | D | ⌉ | |||||||||||||
| ⌊ | -C | -C | 0 ⌊-C | 0 ⌊-C | |||||||||||
| ⌊ | -C | ||||||||||||||
| ⌊ | -C | ||||||||||||||
| ⌊ | -C | ||||||||||||||
| ⌈ | d | -b | ⌉ |
| ⌊ | -c | ⌋ |
- The
(2, 2)-cofactor, which равноa, идет к второй строке и второму столбцу :
| ⌈ | d | -b | ⌉ |
| ⌊ | -c | a | ⌋ |
That’s it! Мы вывели простую формулу для адъюгата матрицы 2x2 !
Как пользоваться этим калькулятором сопряженных матриц?
Пусть случай 2 x 2 не вводит вас в заблуждение: вычисление вспомогательных матриц вручную может занять очень много времени ⌛⌛, особенно если нам приходится иметь дело с большими матрицами. К счастью, наш калькулятор сопряженных матриц может сделать всю эту работу за вас! Вот шаги, которые вы должны выполнить, чтобы эффективно использовать калькулятор сопряженных матриц:
К счастью, наш калькулятор сопряженных матриц может сделать всю эту работу за вас! Вот шаги, которые вы должны выполнить, чтобы эффективно использовать калькулятор сопряженных матриц:
Укажите размер матрицы , для которой нужно найти адъюгат.
Введите коэффициенты вашей матрицы.
Совет: Наш калькулятор сопряженных матриц вводит коэффициенты в матрицу по мере их ввода, поэтому вы можете быстро проверить, все ли в порядке.
Сопряженная матрица отображается в нижней части сопряженной матрицы
калькулятор.
Формула сопряженной матрицы для обращения матрицы
Теперь мы знаем, как найти сопряженную матрицу как вручную, так и с помощью калькулятора сопряженной матрицы, но зачем нам вообще сопряженная матрица ? По одной причине, потому что это очень удобно, когда нам нужно вычислить , обратную матрице .
А именно, когда мы умножаем матрицу на сопряженную, мы получаем диагональную матрицу, диагональные элементы которой равны определителю нашей матрицы:
A * adj(A) = det(A) * I,
, где I — единичная матрица того же размера, что и A . Теперь мы можем вычислить обратное значение как:
A -1 = (1 / det(A)) * adj(A).
То есть, чтобы найти обратную матрицу, нужно умножить ее сопряженную на обратную ее определитель .
Часто задаваемые вопросы
Как рассчитать вспомогательную матрицу?
- Найдите кофактор каждой записи.
- Соберите эти кофакторы в матрицу.
- Транспонировать эту матрицу.
- Наслаждайтесь недавно найденной матрицей сопряженных элементов.
Как найти сопряжение матрицы 2×2?
- Возьмите исходную матрицу.
- Поменять местами элемент по диагонали .

- Изменить знаки антидиагональных элементов, т.е. правого верхнего и левого нижнего элемента.
- Поздравьте себя с нахождением адъюгата!
Как вычислить адъюгат транспонированной матрицы?
Адъюгат транспонированной матрицы, A T , является просто транспонированием адъюгата A :
adj(A T ) = adj(A) T 14 Я вычисляю адъюгат произведения матриц?
Адъюгат произведения двух матриц A и B равен произведению их соответствующих адъюгатов:
adj(AB) = adj(A)adj(B)
Как вычислить адъюгат степени матрицы?
Примыкание матричной мощности Имейте в виду, что в номенклатуре есть некоторая двусмысленность. Сопряжение матрицы может относиться либо к ее сопряженному , то есть транспонирование кофакторной матрицы, или сопряженное транспонирование . A K — K -6 мощности примыкания A :
прил. Как вычислить сопряжение матрицы?

 Обратите внимание, индексы перевернуты!
Обратите внимание, индексы перевернуты! 
 0139
0139 