Первый производный тест — изучите и поймите его онлайн
Американские горки — это одна из первых вещей, которая может привлечь ваше внимание в парке развлечений. Удивительно видеть, как люди кричат от волнения, когда тележка переезжает с одного места на другое! Вы когда-нибудь катались на американских горках?
Типичные американские горки
Есть моменты, когда тележка поднимается, и моменты, когда она опускается. Между ними есть небольшой момент, когда тележка будет выровнена по горизонтали, где вы сможете перевести дыхание.
Точки, в которых это происходит, имеют специальные названия и являются важным объектом изучения в исчислении. Кто сказал, что расчет и веселье несовместимы?
Значение теста первой производной
С тестом первой производной тесно связана концепция стационарной точки . Начнем с его определения.
Пусть \( f \) — дифференцируемая функция. Стационарная точка или критическая точка \(c\) — это значение x, для которого производная \(f\) равна 0. То есть
То есть
\[f'(c)=0.\]
Поскольку производная функции в критической точке равна 0, касательная к функции в этой точке будет иметь наклон 0, т. е. будет горизонтальная линия.
Линии, касающиеся кубической функции в ее критических точках
Функция может иметь более одной критической точки, и Первый тест производной является методом их нахождения. Теперь мы рассмотрим, как выполнить Первый тест на производную 9.0014 .
Первый тест производной — это метод нахождения критических точек дифференцируемой функции \(f.\). Он состоит из следующего:
- Найдите производную функции.
- Вычислите производную функции в критической точке и приравняйте ее к 0, то есть напишите уравнение, утверждающее, что \( f'(c)=0. \)
- Решите уравнение предыдущего шага, чтобы найти значение (я) \ ( c \) внутри области \ ( f \), которые являются критическими точками. 92+6х+10. \]
Используйте тест первой производной, чтобы найти его критические точки.

Ответ:
Прежде всего заметим, что, поскольку ничего другого не указано, можно предположить, что область определения функции состоит из всех действительных чисел. Теперь о шагах:
1. Найдите производную функции.
Данная функция является полиномиальной функцией, поэтому вы можете найти ее производную с помощью степенного правила, то есть
\[f'(x)=2x+6.\]
2. Вычислите производную в критической точке и приравняйте ее к 0.
Сначала вы вычислите производную в критической точке \( c, \), поэтому
\[f'(c)=2c+ 6,\]
и затем вы устанавливаете его равным 0, в результате чего уравнение Полученное уравнение представляет собой линейное уравнение, которое можно решить, выделив \( c, \), то есть
\[\begin{align}2c &= -6 \\ c &= -3.\end{align}\] 92+2x+2, \quad \text{for}\quad x\geq 0.\]
Используйте критерий первой производной, чтобы найти критические точки.
Ответ:
Теперь область определения функции состоит из всех неотрицательных чисел.
 Вы должны следить за этим при решении уравнения на третьем шаге!
Вы должны следить за этим при решении уравнения на третьем шаге!1. Найдите производную функции.
Эту полиномиальную функцию можно дифференцировать по степенному правилу, поэтому
\[h'(x)=2x+2.\]
2. Вычислить производную в критической точке и приравнять ее к 0.
Вычислить \(h'(x)\) в \(x=c,\)
\[h'(c)=2c+2 ,\]
и приравнять его к 0
\[2c+2=0.\]
3. Решить полученное уравнение относительно \( c.\)
Решить полученное уравнение можно в шаг выше, изолируя \(c,\), поэтому
\[\begin{align} 2c &= -2 \\ c &= -1.\end{align}\]
Это значение равно , а не внутри область определения функции, следовательно, функция не имеет критических точек!
Первый производный тест и локальные экстремумы
Критические точки тесно связаны с относительными экстремумами, поэтому, прежде чем продолжить, напомним, что означает экстремум.
Экстремум функции относится либо к максимуму, либо к минимуму.
 2 + 6x + 10\) имеет критическую точку в точке \(-3.\). Теперь взгляните на ее график.
2 + 6x + 10\) имеет критическую точку в точке \(-3.\). Теперь взгляните на ее график.График линии, касательной к функции в ее критической точке
Похоже, что критическими точками являются также точки, в которых функция имеет локальные экстремумы. Это не всегда так, но есть теорема, которая устанавливает эту связь.
Теорема Ферма утверждает, что если функция \(f\) имеет локальный максимум или локальный минимум в точке \(x=c,\) и функция дифференцируема в этой точке, то \(f'(c) =0.\)
Другими словами, теорема Ферма говорит вам, что если функция имеет локальный максимум или локальный минимум в точке, где она дифференцируема, то это критическая точка. Будьте осторожны, чтобы не истолковать эту теорему неправильно, так как есть несколько распространенных ошибок при построении моста между локальными экстремумами и критическими точками. 92=0.\]
3. Решить полученное уравнение относительно \( c.\)
Уравнение, полученное на предыдущем шаге, верно только тогда, когда \(c=0,\), что означает, что существует есть только одна критическая точка в точке \(x=0.
 \)
\)Теперь у вас может возникнуть соблазн предположить, что функция имеет локальный экстремум в точке 0, но это не так. Взгляните на его график.
График кубической функции без локальных экстремумов
Эта кубическая функция не имеет локальных экстремумов , но тем не менее критическая точка находится в \(x=0.\) Обратите внимание, что наклон в критической точке равен 0.
График кубической функции с линией, касательной к критической точке
Вы нашли что не все критические точки являются локальными экстремумами в приведенном выше примере . Давайте теперь рассмотрим еще одну распространенную ошибку.
Рассмотрим функцию
\[g(x)=|x-2|+1.\]
Теперь посмотрим на ее график.
График функции абсолютного значения
Функция имеет относительный минимум в точке \(x=2,\), поэтому у вас может возникнуть соблазн предположить, что это также критическая точка. Однако функция не дифференцируема в точке \(x=2,\), поэтому она является , а не критической точкой.

Теперь вы обнаружили, что не все локальные экстремумы являются критическими точками . Вам нужно, чтобы функция была дифференцируемой в своих относительных экстремумах, чтобы быть критической точкой.
Первый производный тест для функций многих переменных
При поиске информации о тесте первой производной вы можете встретить функции с несколькими переменными. Этот предмет обычно зарезервирован для более высоких уровней, поэтому, если вам достаточно любопытно, погрузитесь в него!
Когда вам дается функция многих переменных, тест первой производной слегка модифицируется. Вам нужно сделать следующее:
- Найти каждую частичную производную функции по всем ее переменным.
- Вычислите каждую частную производную в критической точке и установите их все равными 0. То есть напишите систему уравнений, утверждающую, что каждая частная производная, оцененная в критической точке, равна 0. 92-xy+2y.\]
Найдите его критические точки.

Ответ:
Поскольку его входами являются точки на плоскости, его критические точки будут упорядоченными парами вида \( (a,b). \)
1. Найдите каждую частную производную функции с относительно всех его переменных.
Обе частные производные этой функции можно найти с помощью степенного правила, поэтому
\[\frac{\partial f}{\partial x}=2x-y,\]
и
\[\frac{\partial f}{\partial y}=-x+2.\]
2. Оценить каждую частную производную в критической точке и приравнять их все к 0.
Поскольку критические точки имеют вид \( (a,b),\) оценивают обе частные производные, используя \(x=a\) и \(y=b,\), поэтому
\[\left. \frac{\partial f}{\partial x}\right|_{(a,b)}=2a-b,\]
и
\[\left. \frac{\partial f}{\partial y}\right|_{(a,b)}=-a+2.\]
Приравняв приведенные выше выражения к 0, вы получите систему уравнений
\[\begin{cases}2a-b &= 0 \\ -a+2 &= 0.\end{cases}\]
3.
 S Рассмотрите Систему Уравнений, чтобы найти критические точки .
S Рассмотрите Систему Уравнений, чтобы найти критические точки . Теперь вы можете решить приведенную выше систему уравнений, используя метод по вашему выбору, получив
\[\begin{cases}a &= 2 \\ b &= 4.\end{cases}\]
Это означает, что существует только одна стационарная точка, которая находится в \( (2,4).\)
Обратите внимание, что если функция имеет три переменные, вам придется вычислить все три частные производные и написать три уравнения. В общем, если функция имеет \(n\) переменных, вам понадобятся \(n\) частные производные и \(n\) уравнения. 93-4c=4c(c-1)(c+1).\]
Подставив это обратно в уравнение, вы получите
\[4c(c-1)(c+1)=0,\]
что означает, что
\[4c=0,\]
\[c-1=0,\]
и
\[c+1=0.\]
Решив приведенные выше уравнения, вы можете найти что \( c=0,\) \(c=1,\) и \(c=-1.\) Следовательно, эта функция имеет три критические точки!
Давайте теперь рассмотрим пример с тригонометрической функцией.

Рассмотрим функцию
\[g(x)=\sin{x}.\]
Используйте тест первой производной, чтобы найти критические точки.
Ответ:
1. F инд производная функции.
Производная функции синуса есть функция косинуса, т.е. оно равно 0.
Вычисляя приведенную выше функцию в \(x=c\) 9\pi / _2, \), то есть
\[\pm\frac{\pi}{2},\, \pm\frac{3\pi}{2},\, \pm\frac{5\ pi}{2},\]
и так далее. Вы можете выразить эти нечетные кратные, используя коэффициент \( 2n-1\), потому что вычитание 1 из четного числа дает нечетное число, поэтому
\[c = \left( 2n-1 \right)\frac{ \pi}{2}, \quad \text{ for }\, n=1, 2, 3, \dots .\]
Функция синуса имеет бесконечное количество критических точек!
Тест первой производной и вогнутость
Несмотря на то, что он связан с формой графика, тест первой производной является тестом для нахождения критических точек, но не тестом для нахождения вогнутости графа.
 В этом случае вам следует взглянуть на нашу статью о тесте второй производной.
В этом случае вам следует взглянуть на нашу статью о тесте второй производной.Первый тест производной – ключевые выводы
- стационарная точка или критическая точка – это значение x, для которого производная функции равна 0.
- Первый тест производной состоит в нахождении критической точки функции.
- Вы можете выполнить первый тест производной, выполнив следующие действия:
- Найдите производную функции.
- Вычислите производную функции в критической точке \(c\) и приравняйте ее к 0. То есть запишите уравнение \( f'(c)=0.\)
- Решите приведенное выше уравнение, чтобы найти критические точки. Не забудьте включить только значения внутри домена функции!
- Первый критерий производной связан с локальными экстремумами посредством теоремы Ферма о стационарных точках.
- То, что что-то является критической точкой, не означает, что это локальный экстремум!
Калькулятор n-й производной | Найти производную высшего порядка онлайн
Введение в калькулятор производных высшего порядка
Калькулятор производных n-го порядка — это бесплатный онлайн-инструмент для расчета производных высокого порядка.
 Калькулятор производных высших порядков со ступенями предназначен для поиска нескольких производных функции.
Калькулятор производных высших порядков со ступенями предназначен для поиска нескольких производных функции.Калькулятор производной более высокого порядка — это инструмент, который вычисляет производную в соответствии с пожеланиями пользователя. Он вычисляет высшие производные точно и быстро. Калькулятор производной n-го порядка находит безошибочные результаты.
Что такое n-й калькулятор производных?
Калькулятор высших производных — это онлайн-инструмент, который вычисляет производную любой функции n-й раз. Здесь n-й означает любое число более высокого порядка, т. е. 1,2,3,…
Калькулятор производной n-го порядка — это инструмент, который вычисляет производные более высокого порядка, т. е. когда производная берется в первый раз, он называется 1-м. производная порядка. Когда производная берется во второй раз, она называется второй производной и так далее. Итак, калькулятор n-й производной вычисляет все последовательные производные функции. 9{мн} $$
Как работает n-й решатель производных формул?
Калькулятор производной n-го порядка основан на правилах дифференцирования для нахождения n-й производной функции.

Вот функция [f(x) = xn], у которой взяты первые три последовательные производные.
Первые три производные этой функции:
- f′′(x) = n (n – 1) x n – 2
- f′′′(x) = n (n – 1) (n – 2) x n – 3
Шаги для работы с этим калькулятором:
- Ниже приведены шаги, которые необходимо выполнить для калькулятора n-й производной.
- Откройте страницу калькулятора и загрузите функцию здесь в нужное поле.
- Затем выберите порядок производных из раскрывающегося списка.
- Прежде всего, введите все значения в необходимые поля ввода. Как переменные, так и другие дополнительные значения.
- После ввода всех значений в обязательные поля теперь выберите любое число в поле «ВРЕМЯ», которое спросит вас, сколько раз вы хотите различать функцию.
- Теперь просто нажмите кнопку «Вычислить». Калькулятор энной производной оценит наклон тангенса заданной функции.

- Наконец, результаты заданных вами дифференциальных результатов отображаются на вашем экране.
- После оценки дифференциальной функции обновите страницу для новых вычислений.
Как найти калькулятор высших производных с шагами?
Ниже приведены шаги, которые необходимо выполнить для поиска калькулятора производных высших порядков:
Шаг 1: Введите ключевые слова в строку поиска поисковой системы, такой как Google, Yahoo, Bing или Yandex.
Шаг 2: Вы можете увидеть некоторые из лучших результатов вашего соответствующего запроса «Калькулятор производной n-й степени» или «Калькулятор производной более высокого порядка».
Шаг 3: Надеюсь, мы будем в топе поисковой выдачи, вы можете узнать нас по https://derivative-calculators.com/.
Вот он, откройте инструмент, то есть калькулятор производных высших порядков, поставьте нужную функцию и используйте ее для оценки ваших сложных задач.

Важность калькулятора производных n-го порядка
В математических расчетах использование онлайн-инструмента упрощает расчеты. Перед этими инструментами пользователю приходится выполнять ручные вычисления, что кажется довольно лихорадочным. Таким образом, эти инструменты заменяют это сложное упражнение несколькими умными кликами.
Сегодня пользователи хотят работать не усерднее, а умнее. Итак, этот калькулятор формулы n-й производной специально разработан для вычисления сложных функций.
Ниже приведен список некоторых преимуществ при использовании этого калькулятора производных n-го порядка:
- Калькулятор производных n-го порядка значительно облегчает пользователям расчеты одним щелчком мыши.
- Пользовательский интерфейс калькулятора высокой производной очень удобен.
- Этот калькулятор производных высших порядков дает результаты за доли секунды.
- Улучшает аналитические способности пользователя.


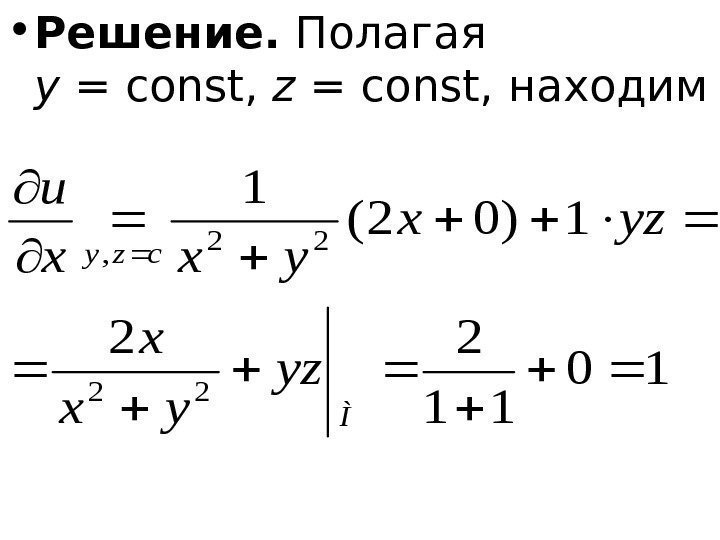
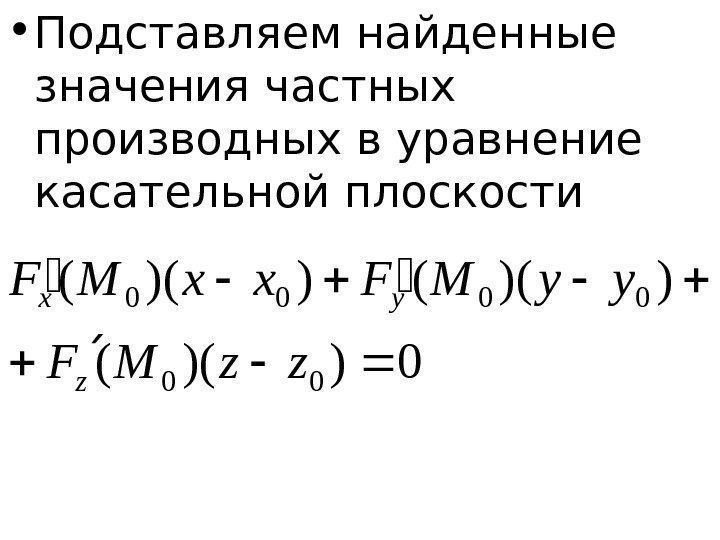 Вы должны следить за этим при решении уравнения на третьем шаге!
Вы должны следить за этим при решении уравнения на третьем шаге! 2 + 6x + 10\) имеет критическую точку в точке \(-3.\). Теперь взгляните на ее график.
2 + 6x + 10\) имеет критическую точку в точке \(-3.\). Теперь взгляните на ее график. \)
\)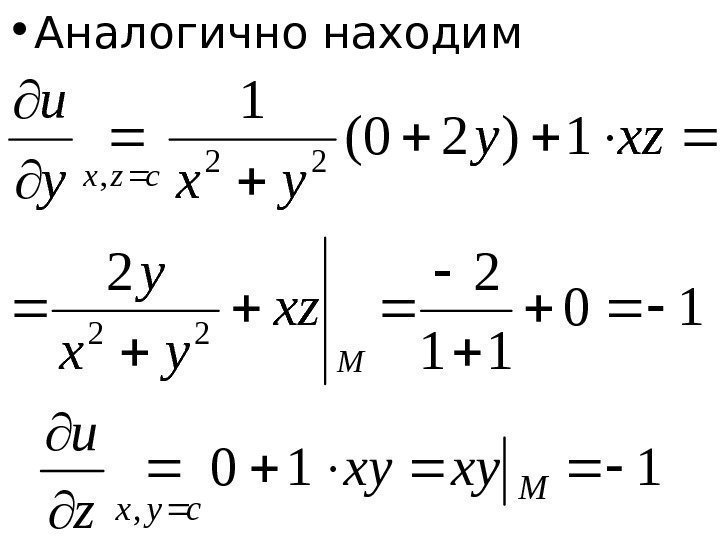

 S Рассмотрите Систему Уравнений, чтобы найти критические точки .
S Рассмотрите Систему Уравнений, чтобы найти критические точки . 
 В этом случае вам следует взглянуть на нашу статью о тесте второй производной.
В этом случае вам следует взглянуть на нашу статью о тесте второй производной. Калькулятор производных высших порядков со ступенями предназначен для поиска нескольких производных функции.
Калькулятор производных высших порядков со ступенями предназначен для поиска нескольких производных функции.


