Определитель 4 порядка. Калькулятор
Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка.
Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.
Пример 1. Вычислить определитель методом разложения.
Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются — выделено красным)
В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников
Найденные значения подставляем в выходной детерминант
Результат легко проверить с помощью матричного калькулятора YukhymCALC .
Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.
Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных
Результаты совпадают, следовательно вычисления проведены верно.
Пример 2. Вычислить определитель матрицы четвертого порядка.
Решение.
Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде
Далее переходим к отысканию определителей по правилу треугольников
Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем
Результат проверяем матричным калькулятором YukhymCALC .
Правильность расчетов подтверждается следующим рисунком
Метод возведения определителя к треугольному виду
Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.
Пример 3. Найти определитель матрицы сведением к треугольному виду
Решение.
Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим
Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем
Дальше целесообразнее от четвертой отнять удвоенную вторую строчку.
В результате элементарных преобразований определитель примет вид
Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе
По свойству, определитель треугольной матрицы равен произведению диагональных элементов.
По желанию можно проверить результат матричным калькулятором.
В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось.
Рассмотрим более сложный.
Пример 4.
Найти определитель матрицы 4-го порядка
Решение.
Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант
Для удобства вычислений, меняем третью строчку со вторым местами..
По свойству определителей любая замена строк местами ведет к изменению знака определителя.
Учитываем это в некотором множителе k=-1.
От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим
Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2.
Результат будет следующим
От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.
Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления
Проверка матричным калькулятором подтверждает правильность производимых вычислений.
Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений.
В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.
Определение четвертого порядка. Определитель матрицы
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!
Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет.
Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .
Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.
Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!
(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)
Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!
Обозначения : Если дана матрица , то ее определитель обозначают .
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.
2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два» :
ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.
Сразу рассмотрим пример:
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Формула длинная и допустить ошибку по невнимательности проще простого.
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Пример:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим шесть нормальных способов для вычисления определителя
Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.
Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.
Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.
В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.
Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.
Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ .
Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)
Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:
Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:
Ну и третий элемент первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:
В следующем примере я раскрыл определитель по четвертому столбцу :
А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя.
БУДЬТЕ ВНИМАТЕЛЬНЫ!
Второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя: ; ; ; detA (детерминант).
.
Пример:
.
Определителем матрицы третьего порядка называется число или математическое выражение, вычисляемое по следующему правилу
Наиболее простым способом вычисления определителя третьего порядка является дописывание снизу определителя двух первых строк.
В образованной таблице чисел перемножаются элементы, стоящие на главной диагонали и на диагоналях параллельных главной, знак результата произведения не изменяется. Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.
Пример:
Разложение определителя по элементам некоторой строки (столбца).
Минором М ij элемента а ij квадратной матрицы А называется определитель, составленный из элементов матрицы А , оставшихся после вычеркивания i- ой строки и j -го столбца.
Например, минором к элементу а 21 матрицы третьего порядка
будет определитель
.
Будем говорить, что элемент а ij занимает четное место, если i+j (сумма номеров строки и столбца на пересечении которых находится данный элемент) — четное число, нечетное место, если i+j — нечетное число.
Алгебраическим дополнением А ij
элемента а ij квадратной матрицы А называется выражение (или величина соответствующего минора, взятого со знаком «+», если элемент матрицы занимает четное место, и со знаком «-», если элемент занимает нечетное место).Пример:
а 23 = 4;
— алгебраическое дополнение элемента а 22 = 1.
Теорема Лапласа . Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.
Проиллюстрируем на примере определителя третьего порядка. Вычислить определитель третьего порядка разложением по первой строке можно следующим образом
Аналогично можно вычислить определитель третьего порядка, разложив по любой строке или столбцу. Удобно раскладывать определитель по той строке (или столбцу), в которой содержится больше нулей.
Пример :
Таким образом, вычисление определителя 3-го порядка сводится к вычислению 3-х определителей второго порядка. В общем случае можно вычислить определитель квадратной матрицы n -го порядка, сводя его к вычислению n определителей (n-1 )-го порядка
Замечание. Не существует простых способов для вычисления определителей более высокого порядка, аналогичных способам вычисления определителей 2-го и 3-го порядка. Поэтому для вычисления определителей выше третьего порядка может использоваться только метод разложения.
Пример . Вычислить определитель четвертого порядка.
Разложим определитель по элементам третьей строки
Свойства определителей:
1. Определитель не изменится, если его строки заменить столбцами и наоборот.
2. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный.
3. Определитель с двумя одинаковыми строками (столбцами) равен 0.
4. Общий множитель всех элементов некоторой строки (столбца) определителя можно вынести за знак определителя.
5. Определитель не изменится, если к элементам одного из его столбцов (строки) прибавить соответствующие элементы любого другого столбца (строки), умноженные на некоторое число.
Пусть имеется квадратная матрица A размером n x n .
Определение. Определителем называется алгебраическая сумма всевозможных произведений элементов, взятых по одному из каждого столбца и каждой строки матрицы A . Если в каждом таком произведении (члене определителя) множители расположены в порядке следования столбцов (т.
е. вторые индексы элементов a ij в произведении расположены в порядке возрастания), то со знаком (+) берутся те произведения, у которых перестановка первых индексов чётная, а со знаком (-) – те, у которых она нечетная.
.
Здесь — число инверсий в перестановке индексов i 1 , i 2 , …, i n .
Методы нахождения определителей
- Определитель матрицы разложением по строкам и столбцам через миноры.
- Определитель методом приведения к треугольному виду (методом Гаусса)
Свойство определителей
- При транспонировании матрицы её определитель не меняется.
- Если поменять местами две строки или два столбца определителя, то определитель изменит знак, а по абсолютной величине не изменится.
- Пусть C = AB где A и B квадратные матрицы. Тогда detC = detA ∙ detB .
- Определитель с двумя одинаковыми строками или с двумя одинаковыми столбцами равен 0. Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.
- Определитель с двумя пропорциональными строками или столбцами равен 0.
- Определитель треугольной матрицы равен произведению диагональных элементов. Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали.
- Если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число.
- Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
- Теорема Якоби: Если к элементам некоторого столбца определителя прибавить соответствующие элементы другого столбца, умноженные на произвольный множитель λ, то величина определителя не изменится.
Таким образом, определитель матрицы остается без изменения, если:
- транспонировать матрицу;
- прибавить к какой-либо строке другую строку, умноженную на любое число.
Задание 1 . Вычислить определитель, разлагая его по строке или столбцу.
Решение :xml :xls
Пример 1 :xml :xls
Задание 2 . Вычислить определитель двумя способами: а) по правилу «треугольников»; б) разложением по строке.
Решение .
а) Слагаемые, входящие в со знаком «минус», строятся таким же образом относительно побочной диагонали.
| = |
= 2 0 0 — 2 4 2 — (-1) 2 0 + (-1) 1 2 + (-2) 2 4 — (-2) 1 0 = -34
б) Запишем матрицу в виде:
| A = |
|
Главный определитель:
∆ = 2 (0 0-2 4)-(-1 (2 0-2 1))+(-2 (2 4-0 1)) = -34
Задание 3 .
Укажите, чему равен определитель квадратной матрицы A четвертого порядка, если ее ранг r(A)=1.
Ответ: det(A) = 0.
«Если Вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи ,
то решайте их .»
Д. Пойа (1887-1985 г.)
(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
С каждой квадратной матрицей связывают число . Это число называется определителем матрицы. Определитель вычисляется по особым правилам и обозначается |A|, det A , ΔA.
Число строк (столбцов) определителя называется его порядком .
Определитель первого порядка матрицы равен элементу a 11: |A|=a 11
Не путать определитель первого порядка с модулем.
Определитель второго порядка обозначается символом
и равен |A|=a 11 a 22 -a 12 a 21
Определитель 3-го порядка обозначается символом
Для запоминания этой формулы используют схематические правила (правило треугольника или Саррюса )
Правило Саррюса.
Правило треугольника.
Посмотрим на примере, как используются эти правила.
ПРИМЕР:
Правило Саррюса
Допишем к определителю два первых столбца.
Правило треугольника
Такой способ вычисления определителей не подходит для определителей 4-го порядка и выше. Прежде чем указать правило, которое позволяет находить определители любого порядка, рассмотрим понятие алгебраического дополнения элемента матрицы.
Алгебраическим дополнением (А ij ) элемента а ij определителя матрицы А называется число, равное произведению (-1) i+j (в степени номер строки плюс номер столбца этого элемента) на определитель, который получается из данного в результате вычеркивания строки и столбца, где стоит этот элемент.
ПРИМЕР:
Вычислить алгебраическое дополнение А 21 элемента а 21 .
РЕШЕНИЕ:
По определению алгебраического дополнения
Вычисление определителя произвольного порядка.
Определитель равен сумме произведений элементов любой его строки (или столбца) на соответствующие алгебраические дополнения.
, разложение определителя 4-го порядка по первой строке выглядит следующим образом:
линейная алгебра — Помогите найти определитель матрицы 4×4?
Извините за отсутствие обозначений, но работать будет легко, если вы знаете, что делаете. Хорошо, моя проблема в том, что в книге говорится, что это можно сделать, расширив любой столбец или строку, но единственный способ получить то, что делает книга в их практическом примере, — это выбрать строку, которую они выбрали. Это беспокоит меня. Поскольку я должен быть в состоянии сделать это так, как я считаю нужным. Я опубликую свою работу, и кто-нибудь укажет на проблему в моей работе. Матрица выглядит следующим образом:
$$А = \влево( \begin{матрица} 5&-7&2&2\\ 0&3&0&-4\\ -5&-8&0&3\\ 0&5&0&-6\\ \end{матрица} \right) $$
Я решил расширить первую строку и вычеркнуть столбцы, чтобы найти второстепенные.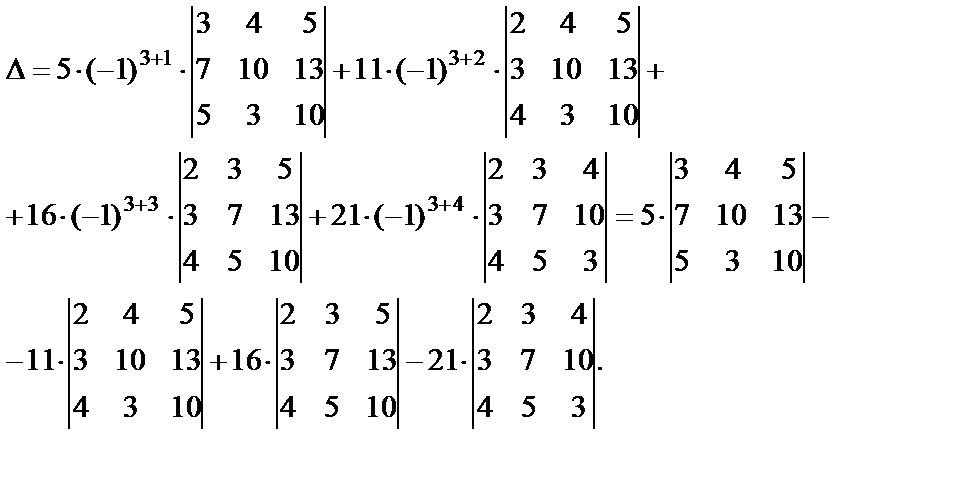
2 = 1$. Это должно быть умножено на определитель минора. Теперь, найдя определитель, я сделал:
3 раза $$ \begin{pматрица} 0 и 3 \\ 0 и -6 \\ \end{pматрица} $$ давая $ 3 (0-0) = 0 $ затем:
0 раз $$ \begin{pматрица} -8 и 3\\ 5 и -6\\ \end{pматрица} $$
дает 0(48-15)=0
Тогда: 4 раза $$ \begin{pматрица} -8 и 0 \\ 5 и 0 \\ \end{pматрица} $$ давая $ 4 (0-0) = 0 $ складывая определители получаем $0+0+0=0$ Итак, det M1 $= 0(1) = 0$
93 = -1$$$ \begin{pматрица} 0 & 0 & -4 \\ -5 & 0 & 3 \\ 0 & 0 & -6 \\ \end{pматрица} $$
о* $$ \begin{pматрица} 0 и 3 \\ 0 и -6 \\ \end{pматрица} $$ давая $ 0 (0-0) = 0 $
, очевидно, что следующая матрица будет выглядеть так же, как верхний член во втором столбце равен нулю, поэтому определитель для этого будет равен $ 0 $. Теперь, наконец,
4 раза $$ \begin{pматрица} -8 и 0 \\ 5 и 0 \\ \end{pматрица} $$ давая 4 (0-0) = 0 94 = 1$
$$ \begin{pматрица} 0 и 3 и -4 \\ -5&-8&3\ 0 и 5 и -6 \\ \end{pматрица} $$
для определителя:
0 раз $$ \begin{pматрица} -8 и 3\ 5 и -6 \\ \end{pматрица} $$ что дает $0(48-15)=0$
-3 раза $$ \begin{pматрица} -5&3\\ 0 и -6 \\ \end{pматрица} $$
, что дает $-3(30-0)= -90$
отсюда продолжать избыточно, потому что после окончательного вычисления для этого минора я получаю -100 и в результате получаю det M3 = -190 и получаю определитель нулей для следующего определителя M4.
что дает: $ 0 (5) + 0 (-7) + (-90) (2) + (0) (2) $ дает
Det Ax $= -380.$ В книге написано, что это 20$, и когда я сделал это на калькуляторе, получилось 20, но проблема в том, что и книга, и калькулятор расширяются по строке с наибольшим количеством нулей, но теоретически говоря, НЕЗАВИСИМО КАКАЯ строка или столбце, который вы решили расширить, вы должны получить тот же ответ. Так что же это? Мои вычисления неверны или мое предположение о том, что вы можете расширяться по любой строке или столбцу, неверно? Разве это не важно, только если определитель не равен нулю? или точное значение имеет значение в более сложных случаях?
линейная алгебра — определитель Вандермонда для порядка 4
спросил
Изменено 9 лет, 1 месяц назад
Просмотрено 2к раз
$\begingroup$
Я хочу показать случай $n=4$ для определителя Вандермонда.