Таким образом, искомый орт вектора $\bar{a}$ имеет координаты $\bar{e}=\left(-\frac{1}{\sqrt{2}} ; \frac{1}{\sqrt{2}}\right)$
Ответ. $\bar{e}=\left(-\frac{1}{\sqrt{2}} ; \frac{1}{\sqrt{2}}\right)$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны точки $A(3 ;-1 ; 4)$ и $B(2 ; 0 ; 2)$ . Найти орт вектора $\overline{A B}$
Решение. Найдем координаты вектора $\overline{A B}$, для этого из координат конца вектора (точки $B$ ) вычтем соответствующие координаты начала (точки $A$ ):
$$\overline{A B}=(2-3 ; 0-(-1) ; 2-4)=(-1 ; 1 ;-2)$$
Для нахождения орта полученного вектора воспользуемся формулой
$$\bar{e}=\frac{a_{x} \cdot \bar{i}+a_{y} \cdot \bar{j}+a_{z} \cdot \bar{k}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$$
Подставим в неё координаты вектора $\overline{A B}$, будем иметь:
$$\bar{e}=\frac{-1 \cdot \bar{i}+1 \cdot \bar{j}-2 \cdot \bar{k}}{\sqrt{(-1)^{2}+1^{2}+(-2)^{2}}}=\frac{-1 \cdot \bar{i}+1 \cdot \bar{j}-2 \cdot \bar{k}}{\sqrt{1+1+4}}=$$ $$=\frac{-1 \cdot \bar{i}+1 \cdot \bar{j}-2 \cdot \bar{k}}{\sqrt{6}}=-\frac{1}{\sqrt{6}} \cdot \bar{i}+\frac{1}{\sqrt{6}} \cdot \bar{j}-\frac{2}{\sqrt{6}} \cdot \bar{k}$$
Таким образом, орт вектора $\overline{A B}$ имеет координаты $\bar{e}=\left(-\frac{1}{\sqrt{6}} ; \frac{1}{\sqrt{6}} ;-\frac{2}{\sqrt{6}}\right)$
Ответ. $\bar{e}=\left(-\frac{1}{\sqrt{6}} ; \frac{1}{\sqrt{6}} ;-\frac{2}{\sqrt{6}}\right)$
$\bar{e}=\left(-\frac{1}{\sqrt{6}} ; \frac{1}{\sqrt{6}} ;-\frac{2}{\sqrt{6}}\right)$
Читать дальше: как найти вектор по точкам.
Поток векторного поля: теория и примеры
- Понятие потока векторного поля и его вычисление как поверхностного интеграла
- Направление и интенсивность потока векторного поля
- Вычисление потока векторного поля: примеры
Своим названием поток векторного поля обязан задачам
гидродинамики о потоке жидкости. Поток векторного поля может быть вычислен в виде поверхностного
интеграла, который выражает общее количество жидкости, протекающей в единицу времени через некоторую
поверхность в направлении вектора скорости течения жидкости в данной точке. Понятие потока векторного поля
обобщается также на магнетический поток, поток электричества, поток тепла через заданную поверхность и
другие. Поток векторного поля может быть
вычислен в виде поверхностного интеграла как первого, так и
второго рода и далее мы дадим его вывод через эти интегралы.
Пусть в некоторой области пространства задано векторное поле
и поверхность σ, в каждой точке M которой определён единичный вектор нормали . Пусть также направляющие косинусы этого вектора — непрерывные функции координат x, y
, z точки M.Определение потока векторного поля. Потоком W поля вектора через поверхность σ называется поверхностный интеграл
или
.
Обозначим как an проекцию вектора на на единичный вектор . Тогда поток можем записать как поверхностный интеграл первого рода
.
По формуле скалярного произведения векторов
.
Учитывая, что
поток векторного поля можно вычислить и как поверхностный интеграл второго рода
.
Поток векторного поля зависит от местоположения поверхности σ. Если
поверхность размещена так, что во всех её точках вектор поля
образует с вектором нормали поверхности острый угол, то проекции вектора
Через каждую точку поверхности проходит одна векторная линия, поэтому поверхность σ пересекает бесконечное множество векторных линий. Однако условно можно принять, что поверхность σ пересекает некоторое конечное число векторных линий. Поэтому можно считать, что поток векторного
поля — это число векторных линий, пересекающих поверхность σ. Чем интенсивнее поток векторного
поля, тем более плотно расположены векторные линии и в результате получается бОльший поток жидкости.
Если поток векторного поля — поле скорости
частиц текущей жидкости через поверхность σ, то поверхностный интеграл
равен количеству жидкости,
протекающей в единицу времени через поверхность σ. Если рассматривать магнетическое поле, которое
характеризуется вектором магнетической индукции ,
то поверхностный интеграл
называется магнетическим потоком через поверхность σ и равен общему количеству линий магнетической
индукции, пересекающих поверхность σ. В случае электростатического поля интеграл
выражает число линий
электрической силы, пересекающих поверхность σ. Этот интеграл называется потоком вектора
интенсивности электростатического поля
через поверхнсть σ. В теории теплопроводности рассматривается стационарный поток тепла через
поверхность σ. Если k — коэффициент теплопроводности, а u(M) —
температура в данной области, то поток тепла, протекающего через поверхность σ в единицу времени,
определяет интеграл .
Пример 1. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
Решение.
1) Поверхностью σ является треугольник ABC, а её проекцией на ось xOy — треугольник AOB.
Координатами вектора нормали данной поверхности являются коэффициенты при переменных в уравнении плоскости:
.
Длина вектора нормали:
.
Единичный вектор нормали:
.
Таким образом,
Из выражения единичного вектора нормали следует, что направляющий косинус . Тогда .Теперь можем выразить поток векторного поля в виде поверхностного интеграла первого рода и начать решать его:
Выразим переменную «зет»:
Продолжаем вычислять интеграл и, таким образом, поток векторного поля:
Получили ответ: поток векторного поля равен 64.
2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем
.
Представим этот интеграл в виде суммы трёх интегралов и каждый вычислим отдельно.
Учитывая, что проекция поверхности на ось yOz является треугольник OCB, который ограничивают прямые
Проекцией поверхности на ось xOz является треугольник OAC, который ограничен прямыми x = 0, z = 0, 2x + 3z = 6 или . По этим данным получаем второй интеграл, который сразу решаем:
Проекцией поверхности на ось xOy является треугольник OAB, который ограничен прямыми x = 0, y = 0,
2x + y = 6. Получаем третий интеграл и
решаем его:
Получаем третий интеграл и
решаем его:
Осталось только сложить все три интеграла:
.
Получили ответ: поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.
Нет времени вникать в решение? Можно заказать работу!
Пример 2. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
Решение. Данная поверхность представляет собой треугольник ABC, изображённый на рисунке ниже.
1) Коэффициенты при x, y и z из уравнения плоскости являются координатами вектора нормали
плоскости, которые нужно взять с противоположным знаком (так как вектор нормали верхней стороны
треугольника образует с осью Oz острый угол, так что третья координата
вектора нормали плоскости должна быть положительной).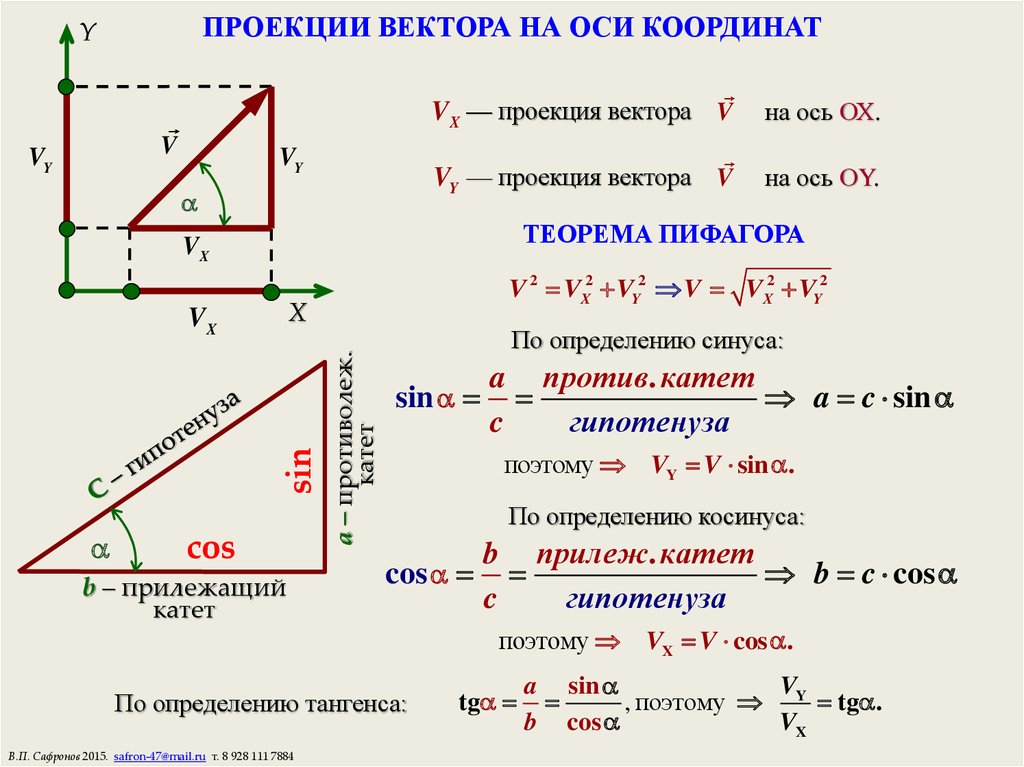
.
Длина этого вектора:
,
единичный вектор нормали (орт):
.
Скалярное произведение векторного поля и единичного нормального вектора:
Поток векторного поля, таким образом, представим в виде поверхностного интеграла первого рода
.
Выразим «зет» и продифференцируем то, что уже можно продифференцировать:
Вычисляем интеграл:
2) Представим поток векторного поля в виде поверхностного интеграла второго рода:
.
Первый и второй интегралы берём со знаком «минус», так как вектор нормали поверхности образует с осями Ox и Oy тупой угол.
Вычисляем первый интеграл:
Вычисляем второй интеграл:
Вычисляем третий интеграл:
Складываем три интеграла и получаем тот же самый результат:
.
Пример 3. Вычислить поток векторного поля через внешнюю сторону параболоида в первом октанте, отсечённую плоскостью z = 9.
Поток векторного поля представим в виде поверхностного интеграла второго рода:
Второй интеграл берём со знаком минус, так как нормальный вектор поверхности образует с осью Oz тупой угол. Вычисляем первый интеграл:
Вычисляем второй интеграл:
В сумме получаем искомый поток векторного поля:
.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Поделиться с друзьями
Векторный калькулятор онлайн — Solumaths
Векторный калькулятор, расчет онлайн
Сводка:
Векторный калькулятор позволяет выполнять вычисления с векторами, используя координаты.
vector_calculator онлайн
Описание:
Векторный калькулятор позволяет вычислить векторов из декартовых координат.
Векторный онлайн-калькулятор позволяет выполнять арифметические операции над векторами, он позволяет суммировать, разность или умножать вектор на скаляр. Векторный калькулятор позволяет использовать как буквальные координаты , так и числовые координаты . Векторный калькулятор определяет различные этапы расчета Векторный калькулятор — это инструмент, особенно подходящий для аналитической геометрии.
- Арифметические операции с использованием векторов координат
- Расчет векторов и буквенных координат
Чтобы выполнить следующий расчет `((3),(4),(5))+((1),(2),(3))-((2),(4),(5))` с использованием координат векторы
входить
vector_calculator(`[3;4;5]+[1;2;3]-[2;4;5]`),
после расчета возвращается результат.
Изюминкой векторного калькулятора является его способность выполнять буквальные вычисления, т. е. символьные вычисления. по координатам векторов.
Чтобы выполнить следующий расчет `((a),(2a),(5a))+((0),(-a),(c))-((1+a),(4+c),(5 ))` включая векторы координат, содержащие буквы, входить vector_calculator(`[a;2a;5a]+[0;-a;c]-[1+a;4+c;5]`), после расчета возвращается результат.
Синтаксис:
vector_calculator(выражение)
Примеры:
- vector_calculator(`[1;1;1]+[5;5;6]`), возвращает [6;6;7]
- vector_calculator(`[1;1;1]-[5;5;6]`), возвращает [-4;-5;-5]
- vector_calculator(`6*[1;1;1]-[5;5;6]`), возвращает [1;1;0]
Расчет онлайн с помощью vector_calculator (векторный калькулятор)
См. также
также
Список связанных калькуляторов:
- Векторный калькулятор : vector_calculator.
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты. - Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
- Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
- Вычисление разности двух векторов : vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- Вычисление нормы вектора: vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
- Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.

- Произведение вектора на число: product_vector_number. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
- Калькулятор перекрестного произведения: перекрестное_произведение. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
- Вычисление суммы двух векторов: vector_sum. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Напоминания о курсах, калькуляторы, упражнения и игры: Векторы
Калькулятор величины вектора — Найдите величину вектора
Онлайн-калькулятор величины вектора поможет вам определить величину векторов 2D, 3D, 4D и 5D по заданным координатам или точкам представления вектора. Кроме того, этот калькулятор длины вектора вычисляет вектор по начальной и конечной точкам, используя свою формулу. Читайте дальше, чтобы узнать, как найти величину вектора. Начнем с основ!
Начнем с основ!
Вектор имеет величину (длину) и направление. Чтобы найти величину вектора, нам нужно вычислить длину вектора. Такие величины, как перемещение, скорость, импульс, сила и т. д., являются векторными величинами. Но Масса, объем, расстояние, температура и т. д. являются скалярными величинами. Скаляр имеет только величину, и он имеет то же направление и величину. Величина векторной формулы используется для определения длины этого вектора и используется для представления | v |, так что это значение в основном представляет собой длину между начальной и конечной точкой вектора. 92)} в 5-мерном пространстве и так далее…
Это некоторые формулы для различных измерений, которые используются калькулятором векторной величины.
Однако онлайн-калькулятор угла между двумя векторами позволяет найти угол, величину и скалярное произведение между двумя векторами.
Как найти модуль вектора? Количество компонентов вектора зависит от размеров пространства. Обычно мы имеем дело с 2D- и 3D-векторами с тремя разными компонентами. В декартовых координатах мы можем использовать значения компонентов a, b и c. Для получения сферических координат удобно использовать значения двух углов θ и φ и длину вектора в прямом смысле. Другими словами, трехмерное расстояние между началом и концом вектора.
Обычно мы имеем дело с 2D- и 3D-векторами с тремя разными компонентами. В декартовых координатах мы можем использовать значения компонентов a, b и c. Для получения сферических координат удобно использовать значения двух углов θ и φ и длину вектора в прямом смысле. Другими словами, трехмерное расстояние между началом и концом вектора.
Однако используйте калькулятор формулы расстояния, который поможет вам рассчитать расстояние между любыми двумя точками.
Как работает калькулятор векторной величины?Онлайн-величина векторного калькулятора находит длину векторов для введенных координат или начальной и конечной точек, следуя этим инструкциям: вниз список.
- Калькулятор векторной величины вычисляет длину вектора.

- Отображает величину вектора по формуле для расчета его длины с пошаговыми вычислениями.
Список типов векторов
- Нулевой вектор
- Единичный вектор
- Первоначальный вектор
- Вектор положения
- Коллинеарный вектор
- Копланарный вектор
- Нравится и не нравится векторам
- Равный вектор
Вектор — это величина с двумя независимыми свойствами: величиной и направлением. Примерами векторов в природе являются импульс, скорость, сила, вес и электромагнитные поля.
Есть указания по размерам? Величина, не зависящая от направления, называется скалярной величиной. Векторные величины имеют два атрибута: направление и величину. Скалярные величины имеют только величину.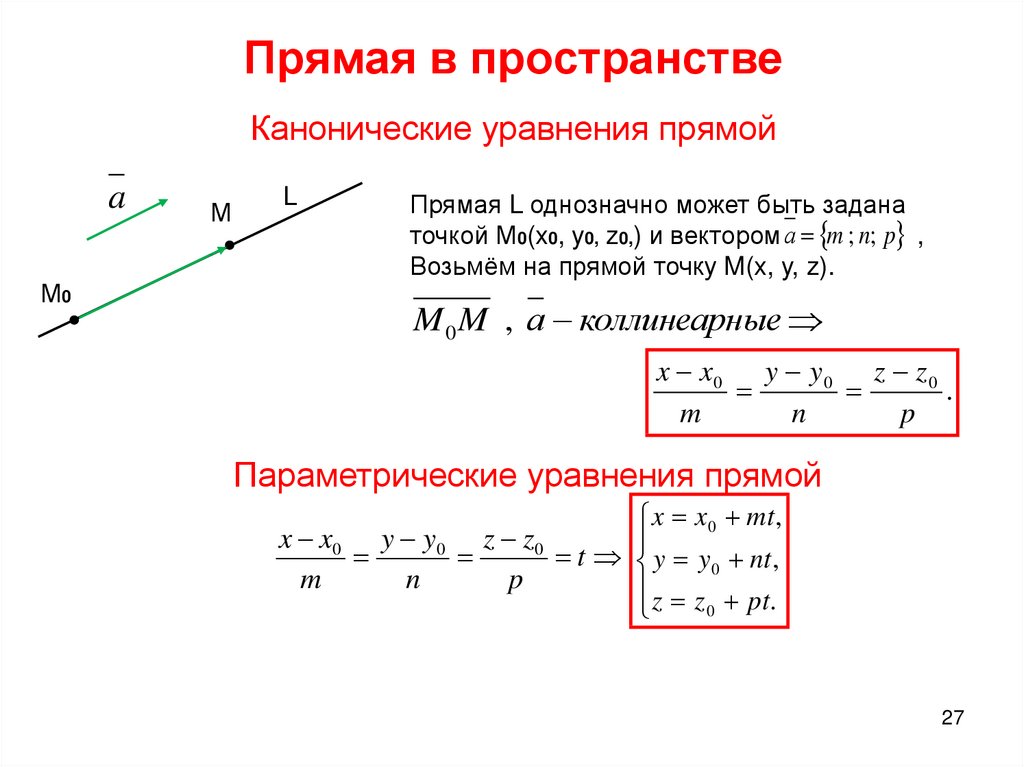

 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
