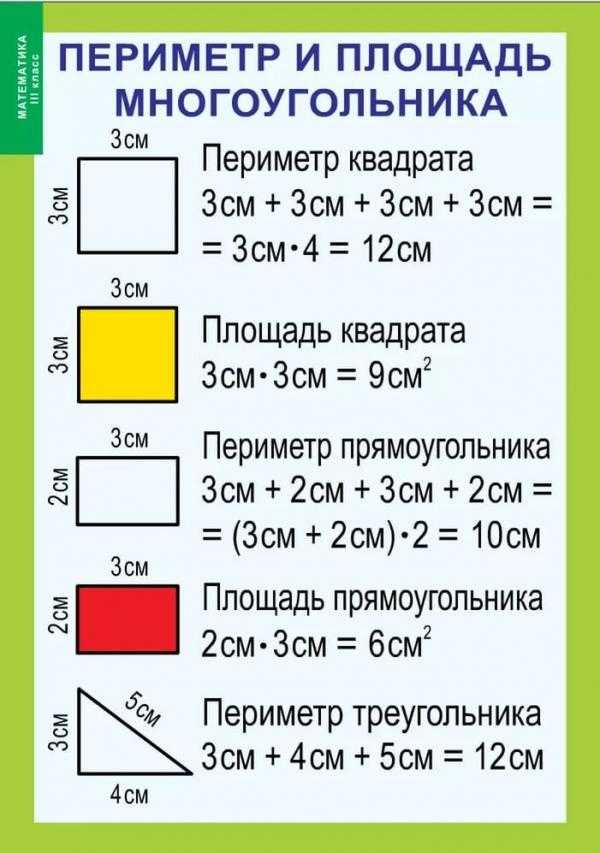
Периметр квадрата формула и калькулятор онлайн
{P = 4 \cdot a}
Найти периметр квадрата
через сторонучерез диагональчерез площадьчерез радиус описанной окружностичерез радиус вписанной окружности
Сторона a
ммсмдммкмдюймы (in)футы (ft)
Результат в
ммсмдммкмдюймы (in)футы (ft)
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат — четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны
{P = 4 \cdot a}
a — сторона квадрата
Формула периметра квадрата через диагональ
{P = 2 \sqrt{2} \cdot d}
d
— диагональ квадратаФормула периметра квадрата через площадь
{P = 4\sqrt{S}}
S — площадь квадрата
Формула периметра квадрата через радиус описанной окружности
{P = 4\sqrt{2} \cdot R}
R — радиус описанной около квадрата окружности
Формула периметра квадрата через радиус вписанной окружности
{P = 8r}
r — радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2. 2} = 16 \cdot 2 = 32 \: см
2} = 16 \cdot 2 = 32 \: см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем — 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде — 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 \cdot a = 4 \cdot 13 = 52 \: см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 \cdot a = 4 \cdot 5 = 20 \: см
Ответ: 20 см
Проверить ответ поможет калькулятор . 2 = 4 \cdot 2 = 8 \: см
2 = 4 \cdot 2 = 8 \: см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор — 2 * sqrt(2).
формула по длине стороны, диагонали
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение периметра квадрата: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.
- Формула вычисления периметра
- По длине стороны
- По длине диагонали
- Примеры задач
Формула вычисления периметра
По длине стороны
Периметр (P) квадрата равняется сумме длин его сторон.
P = a + a + a + a
Так как все стороны квадрата равны, формулу можно представить в виде произведения:
P = 4 ⋅ a
По длине диагонали
Периметр (P) квадрата равен произведению длины его диагонали на число 2√2:
P = d ⋅ 2√2
Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√2.
Примеры задач
Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.
Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.
Задание 2
Найдите периметр квадрата, диагональ которого равняется √2 см.
Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √2 см ⋅ 2√2 = 4 см.
Решение 2:
Выразим длину стороны через диагональ:
a = d / √2 = √2 см / √2 = 1 см.
Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Периметр квадрата – определение, формула, примеры, факты
Периметр квадрата – введение
В геометрии периметр фигуры определяется как общая длина ее границы.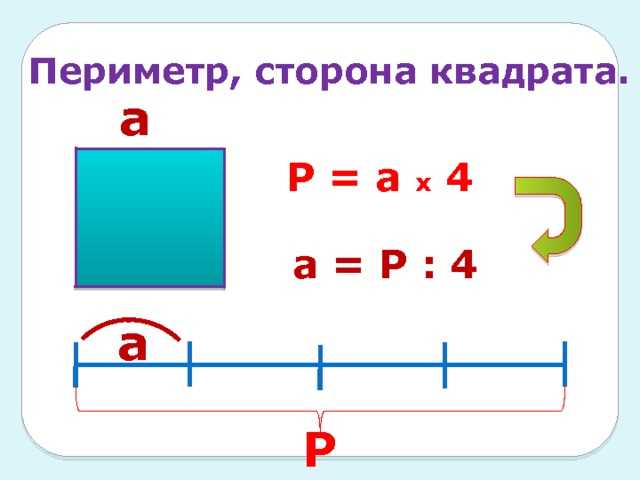 Периметр квадрата определяется сложением длин всех его сторон. Он измеряется в линейных единицах измерения, таких как сантиметры, метры, дюймы или футы.
Периметр квадрата определяется сложением длин всех его сторон. Он измеряется в линейных единицах измерения, таких как сантиметры, метры, дюймы или футы.
Родственные игры
Что такое периметр квадрата?
Периметр квадрата — это сумма длин всех сторон квадрата. Следовательно, мы можем найти периметр квадрата, сложив все его четыре стороны.
Все стороны квадрата равны. Итак, периметр квадрата вычисляется путем четырехкратного сложения стороны квадрата.
Связанные рабочие листы
Формула периметра квадрата
Чтобы вычислить периметр квадрата, мы используем следующую формулу:
P $= 4 \times$ сторона $=$ 4 Формула квадрата
| Периметр общего четырехугольника | $= $Сумма сторон |
| $= a + b + c + d$, где a, b, c и d – стороны четырехугольника |
Поскольку стороны квадрата равны, значит, $a = b = c = d$
Это означает,
| Периметр квадрата | $= a + a + a + a$ |
| $= 4 х |



 2$. Сколько будет стоить ограждение поля, если 1 фут стоит $\$$2,5? 92$
2$. Сколько будет стоить ограждение поля, если 1 фут стоит $\$$2,5? 92$ 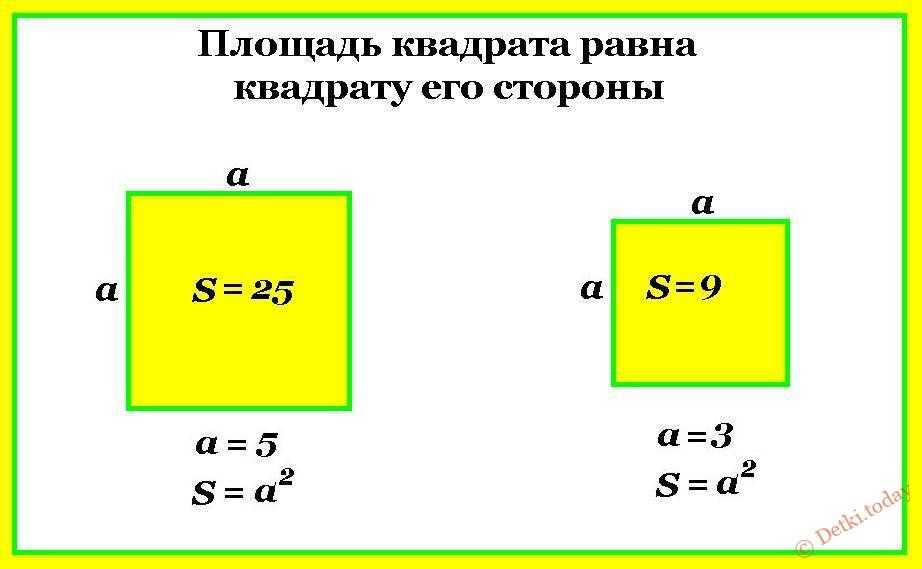
 Длина границы или сторон любой двумерной фигуры называется периметром. Периметр квадрата – это сумма длин всех четырех сторон квадрата.
Длина границы или сторон любой двумерной фигуры называется периметром. Периметр квадрата – это сумма длин всех четырех сторон квадрата. Найдите расстояние, пройденное Шайной.
Найдите расстояние, пройденное Шайной.
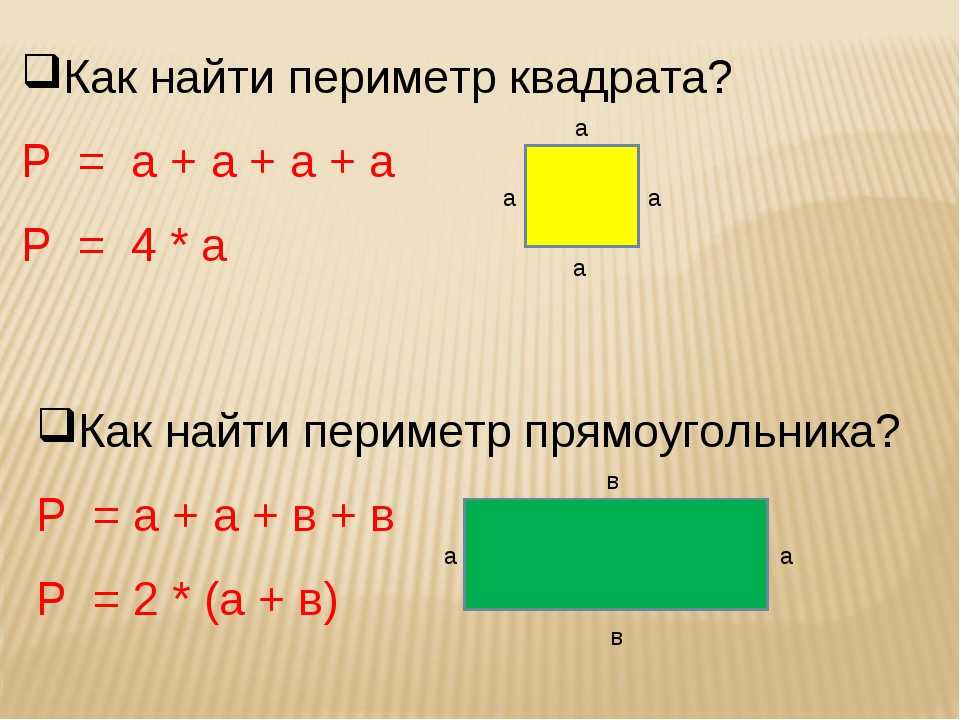 е. 20000.
е. 20000.