| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Найти площадь поверхности цилиндра онлайн
Пример решили: 1516 раз Сегодня решили: 0 раз
Введите длину высоты и радиуса цилиндра
Высота h Радиус r
Вычисление площади поверхности цилиндра
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями.
Цилиндрическая поверхность – поверхность, производимая движением прямой линии AB (образующей),
сохраняющей одно и то же направление и пересекающей данную линию (направляющую).
Часть поверхности, заключенная между параллельными плоскостями, называется боковой поверхностью цилиндра, а части плоскостей, отсекаемые этой поверхностью — основаниями цилиндра. Расстояние между плоскостями называется высотой цилиндра h.
Существуют следующие виды цилиндров:
- Прямой круговой цилиндр – тело, ограниченное круговой цилиндрической поверхностью и двумя параллельными поверхностями, перпендикулярными к образующей. Его основаниями являются круги радиусом r. У такого цилиндра есть ось симметрий.
- Равносторонний цилиндр — цилиндр, осевое сечение которого – квадрат.
- Косой или наклонный цилиндр – если образующая касается основания не под прямым углом.
- Эллиптический цилиндр – если осевое сечение является эллипсом.
2$$ Найти площадь треугольника
Найти площадь поверхности параллелепипеда
Найти площадь поверхности куба
Найти площадь ромба
Найти площадь кругового сектора
- Нахождение объема и площади поверхности цилиндра
2$$Попробуйте другие сервисы
Нахождение объема и площади поверхности цилиндра
Результаты обучения
Если вы когда-нибудь видели банку газировки, то знаете, как выглядит цилиндр. Цилиндр — это объемная фигура с двумя параллельными окружностями одинакового размера вверху и внизу. Верх и низ цилиндра называются основаниями. Высота [латекс]h[/латекс] цилиндра — это расстояние между двумя основаниями. Для всех цилиндров, с которыми мы будем здесь работать, стороны и высота [latex]h[/latex] будут перпендикулярны основаниям.
Цилиндр имеет два круглых основания одинакового размера.
{2}[/латекс]. На изображении ниже показано, как формула [латекс]V=Bh[/латекс] используется для прямоугольных тел и цилиндров.
Увидев, как цилиндр похож на прямоугольное твердое тело, вы сможете легче понять формулу объема цилиндра.
Чтобы понять формулу площади поверхности цилиндра, представьте себе банку с овощами. У него три поверхности: верхняя, нижняя и часть, образующая стенки банки. Если вы аккуратно отрежете этикетку сбоку от банки и развернете ее, то увидите, что это прямоугольник. См. изображение ниже.
Разрезав и развернув этикетку банки с овощами, мы видим, что поверхность цилиндра представляет собой прямоугольник. Длина прямоугольника — это окружность основания цилиндра, а ширина — высота цилиндра.
Расстояние вокруг края банки — это окружность основания цилиндра, а также длина [латекс]L[/латекс] прямоугольной этикетки. Высота цилиндра равна ширине [латекс]W[/латекс] прямоугольной этикетки. Таким образом, площадь этикетки может быть представлена как
.
Чтобы найти общую площадь поверхности цилиндра, мы добавляем площади двух кругов к площади прямоугольника.
Площадь поверхности цилиндра с радиусом [латекс]r[/латекс] и высотой [латекс]h[/латекс] равна 9{2}+2\pi rh[/latex]
Объем и площадь поверхности цилиндра
Для цилиндра с радиусом [латекс]r[/латекс] и высотой [латекс]h:[/латекс]
пример
Цилиндр имеет высоту [латекс]5[/латекс] сантиметров и радиус [латекс]3[/латекс] сантиметров. Найдите 1. объем и 2. площадь поверхности.
Решение
| Шаг 1. Прочтите проблему. Нарисуй рисунок и подпиши это с данной информацией. |
| 1. | |
| Шаг 2. Определите , что вы ищете. | объем цилиндра |
Шаг 3. Имя. Выберите переменную для ее представления. | пусть В = объем |
| Шаг 4. Перевести. Напишите соответствующую формулу. Заменитель. (Используйте [латекс]3.14[/латекс] вместо [латекс]\pi [/латекс] ) 9{2}\cdot 5[/латекс] | |
| Шаг 5. Решить. | [латекс]В\ок. 141,3[/латекс] |
| Шаг 6. Проверка: Мы оставляем вам возможность проверить свои расчеты. | |
| Шаг 7. Ответьте на вопрос. | Объем приблизительно равен [латекс]141,3[/латекс] кубических дюймов. |
| 2. | |
| Шаг 2. Определите 9{2}+2\влево(3.14\вправо)\влево(3\вправо)5[/латекс] | |
| Шаг 5. Решить. | [латекс]S\ок. 150,72[/латекс] |
Шаг 6. Проверка: Мы оставляем вам возможность проверить свои расчеты. | |
| Шаг 7. Ответьте на вопрос. | Площадь поверхности составляет приблизительно [латекс]150,72[/латекс] квадратных дюймов. |
попробовать
пример
Найдите 1. объем и 2. площадь поверхности банки газировки. Радиус основания составляет [латекс]4[/латекс] сантиметра, а высота [латекс]13[/латекс] сантиметров. Предположим, что банка имеет форму цилиндра.
Показать решение
попробуйте
В следующем видео показан пример поиска объема цилиндра.
В следующем примере видео мы покажем, как найти площадь поверхности цилиндра.
Нахождение сеток, объема и площади поверхности цилиндров — Krista King Math
Формулы для объема и площади поверхности прямоугольных цилиндров
В этом уроке мы рассмотрим сети, объем и площадь поверхности цилиндров.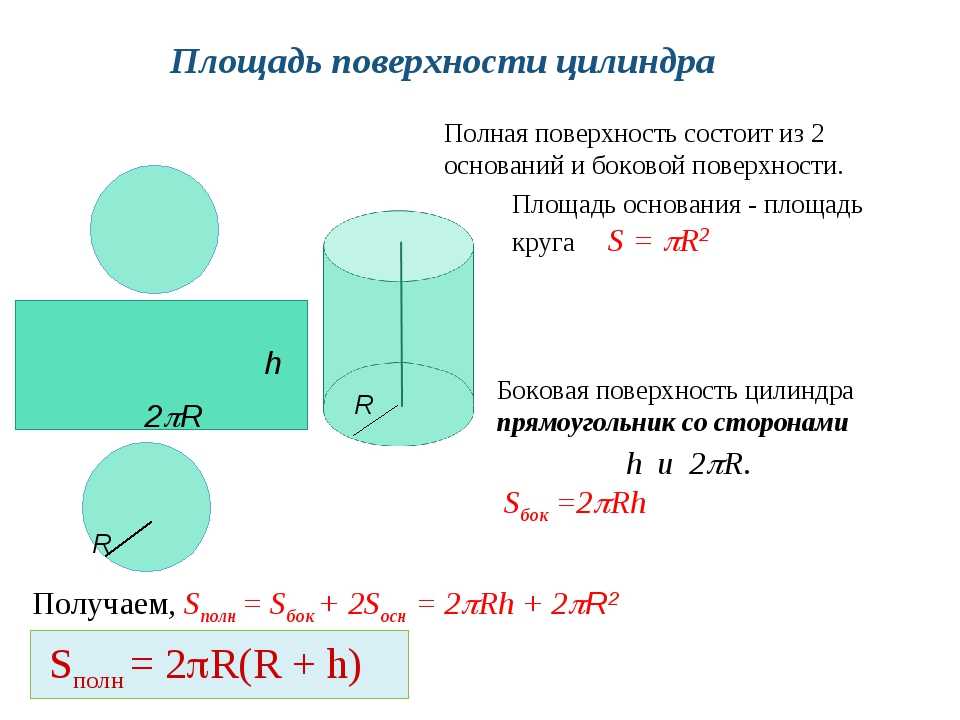
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Цилиндры
Правильный круглый цилиндр (единственный тип цилиндра, с которым мы имеем дело в этом уроке) имеет пару параллельных конгруэнтных круглых оснований.
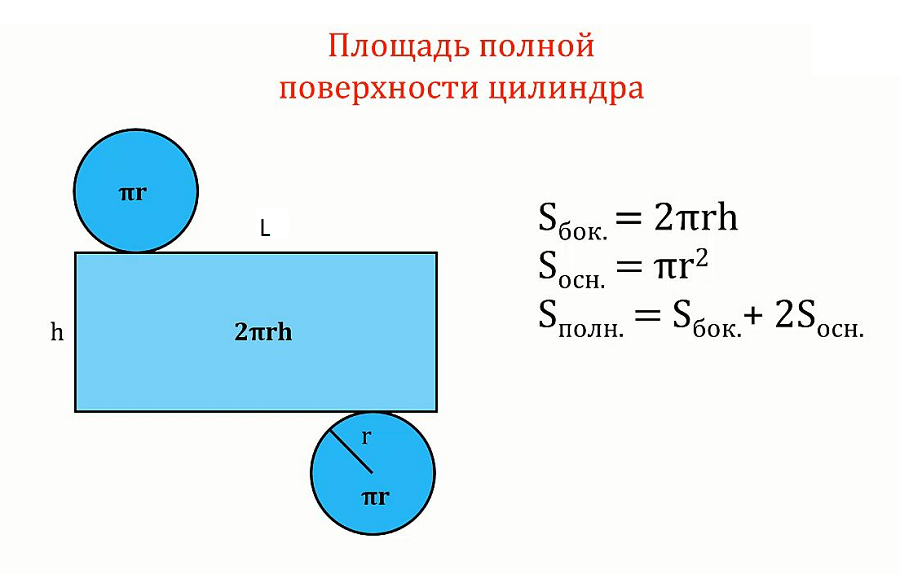
Сеть цилиндра выглядит как прямоугольник с двумя окружностями, прикрепленными к противоположным концам.
Мы также определяем радиус основания цилиндра как радиус основания, а высоту цилиндра как расстояние между основаниями. 9{2}}???
где ???r??? радиус цилиндра и ???h??? это высота цилиндра.
Как найти площадь поверхности цилиндров
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого.
🙂Учить больше
Площадь поверхности боковой стороны цилиндра с учетом нетто
Пример
Какова площадь прямоугольника, изображенного на сетке?
Площадь прямоугольника в сетке цилиндра равна произведению длины окружности (длина горизонтального размера прямоугольника в этой сетке) на высоту цилиндра (длина вертикальный размер прямоугольника в этой сети). Длина окружности равна ???C=2\pi r???, поэтому площадь прямоугольника ???A=2\pi rh???. Вы заметите, что это отображается в первой части формулы площади поверхности цилиндра. 9{2}}???
Теперь мы можем найти высоту.
???1356,48=75,36ч+904,32???
???452.16=75.36ч???
???\frac{452.16}{75.36}=h???
???ч=6\текст{ футов}???
Получить доступ к полному курсу геометрии
Начать
Изучайте математикуКриста Кинг