Найти площадь плоской фигуры ограниченной линиями: Вычислить площадь фигуры, ограниченной линиями

Вычислить площадь фигуры, ограниченную линиями. решение задачи Интегралы с ответом

Пример 1

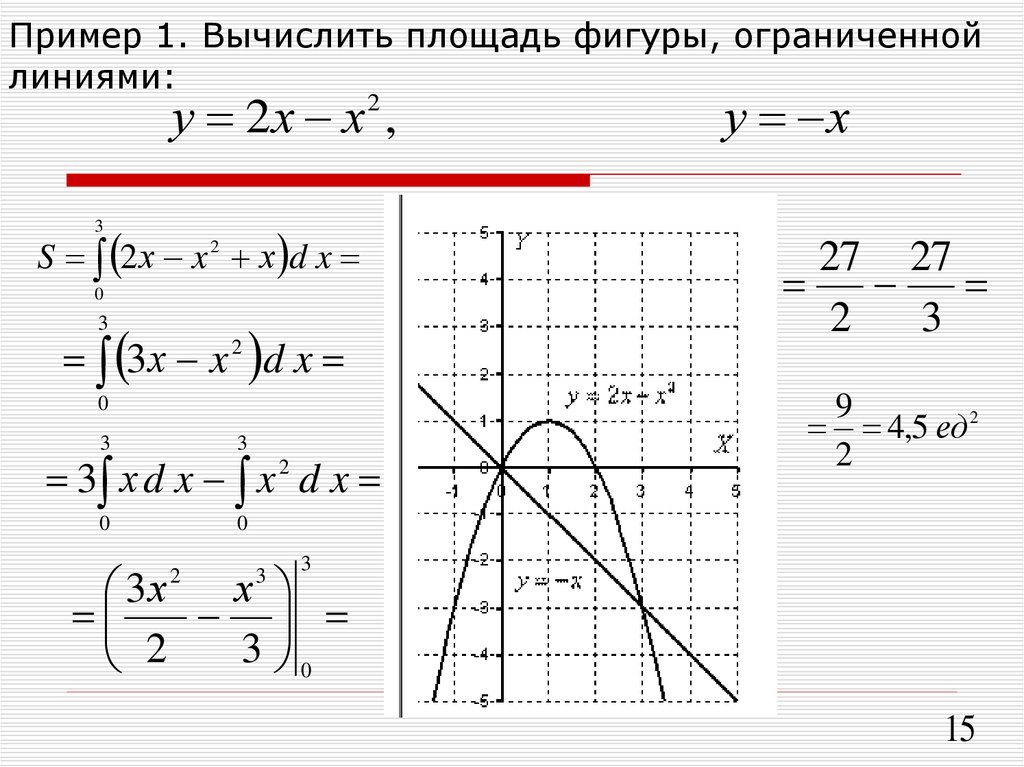
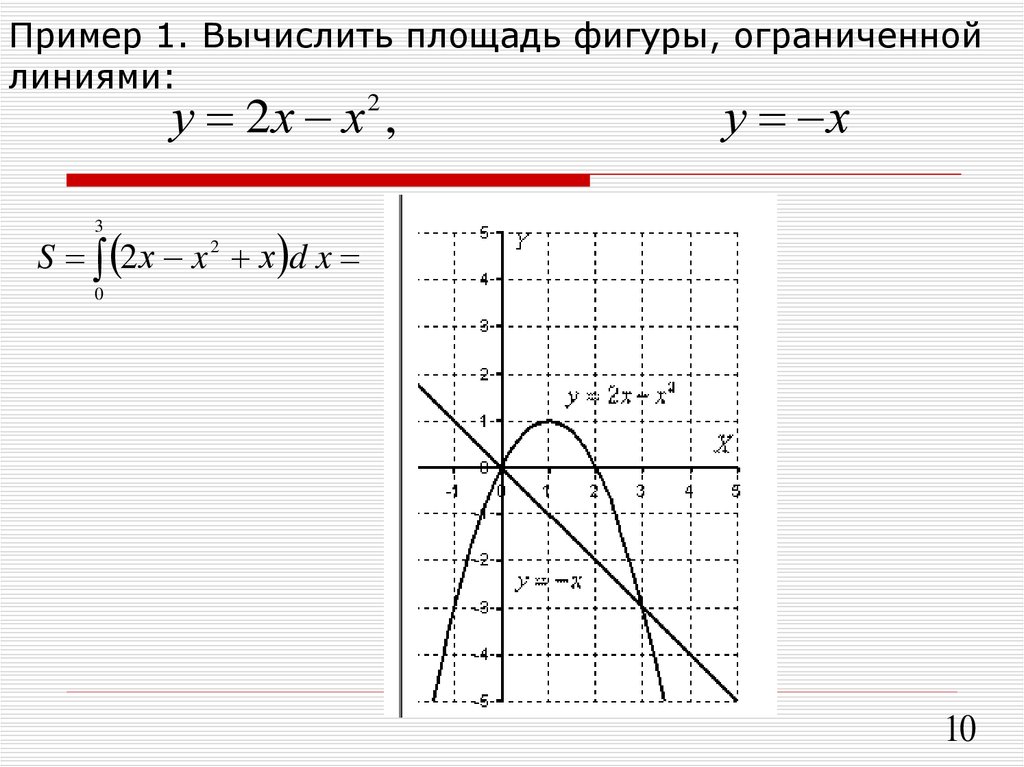
Вычислить площадь фигуры ограниченную линиями:

y=sinx, y = cosx, x = 0.

Пример 2

Найти площадь плоской фигуры с помощью двойного интеграла:

Пример 3

Сделать чертеж области, ограниченной заданными линиями. Вычислить площадь полученной фигуры

Пример 4

Вычислить площадь фигуры, ограниченной параболой , прямой .

Пример 5

Вычислить площадь фигуры, ограниченной графиками функций

Пример 6

Пример 7

Вычислить (с точностью до двух знаков после запятой) площадь фигуры, ограниченной указанными линиями.

Пример 8

Вычислить площадь фигуры, ограниченной осями координат и графиком функции:

Пример 9

Найти площадь фигуры, ограниченной линиями

построить схематический чертеж в декартовых координатах.

Пример 10

Вычислить площадь фигуры, ограниченной линиями:

используя двойной интеграл.

Пример 11

Вычислить площадь фигуры, ограниченной осями координат играфиком функции

Пример 12

Вычислить площадь фигуры, ограниченной линиями

Пример 13

Вычислить площадь фигуры, ограниченной линиями:

Пример 14

Вычислить площади фигур, ограниченных графиками функций.

Пример 15

Вычислить площади фигур, ограниченных графиками функций.

Пример 16

Найти площадь фигуры, ограниченной линиями

построить схематический чертеж в декартовых координатах.

Пример 17

Вычислить площадь фигуры, ограниченной линиями  используя двойной интеграл.

Пример 18

Вычислить площадь фигуры, ограниченной линиями и расположенной в первой четверти координатной плоскости. Сделать чертеж.

Пример 19

С помощью определённого интеграла вычислить площадь области D, ограниченной заданными линиями.

Пример 20

Вычислить площадь фигуры, ограниченной графиками функций:

Пример 21

Вычислите площадь фигуры, ограниченной линиями:

y=4x-x² ;  y=0

Пример 22

Найти площадь фигуры, ограниченной линиями:

Пример 23

Найти площадь фигуры, ограниченной линиями:

Пример 24

Найти площадь фигуры, ограниченной линией:

Пример 25

Найти площадь фигуры, ограниченной линиями:

Пример 26

Найти площадь фигуры, ограниченной графиком функции прямыми .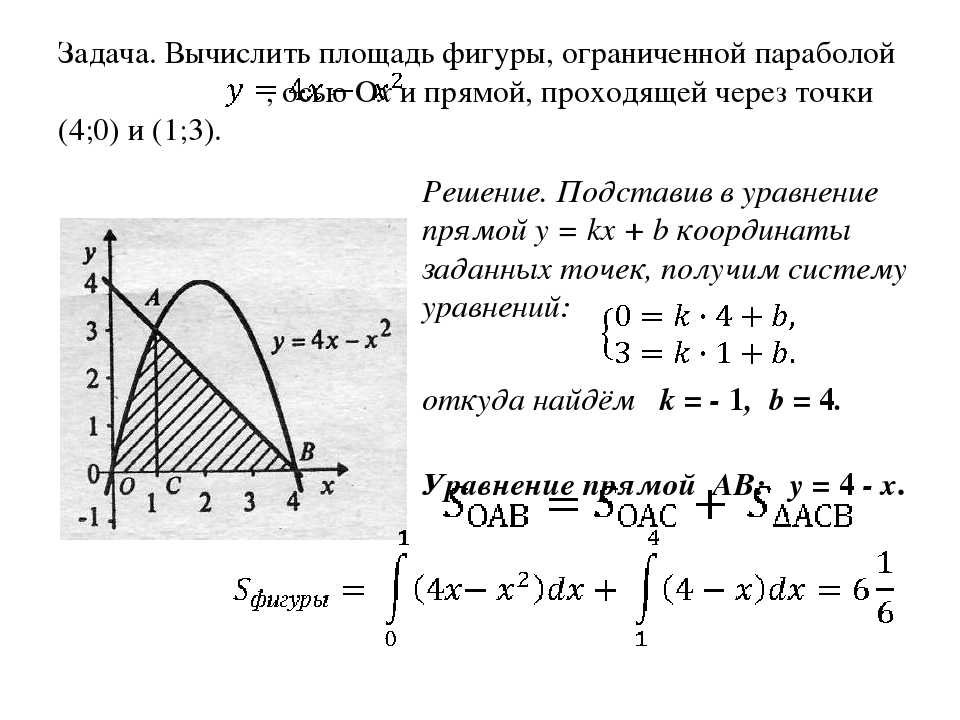

Пример 27

Вычислить площадь фигуры, ограниченной линиями.

Пример 28

Вычислить площадь фигуры, ограниченной линиями.

Пример 29

Найти площадь фигуры, ограниченной линиями: 

Пример 30

Вычислить площадь фигуры, ограниченной линиями:

Пример 31

Вычислить площадь фигуры, ограниченной линиями x²  =  y +2 и y =-x.

Пример 32

Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж области.

Пример 33

Найти площадь фигуры, ограниченной линиями

Из данной статьи вы узнаете, как найти площадь фигуры, ограниченной линиями, используя вычисления с помощью интегралов. Впервые с постановкой такой задачи мы сталкиваемся в старших классах, когда только-только пройдено изучение определенных интегралов и пора приступить к геометрической интерпретации полученных знаний на практике.

Итак, что потребуется для успешного решения задачи по поиску площади фигуры с помощью интегралов:

• Умение грамотно строить чертежи;
• Умение решать определенный интеграл с помощью известной формулы Ньютона-Лейбница;
• Умение «увидеть» более выгодный вариант решения — т. е. понять, как в том или ином случае будет удобнее проводить интегрирование? Вдоль оси икс (OX) или оси игрек (OY)?
• Ну и куда без корректных вычислений? ) Сюда входит понимание как решать тот иной тип интегралов и правильные численные вычисления.

Алгоритм решения задачи по вычислению площади фигуры, ограниченной линиями:

1. Строим чертеж. Желательно это делать на листке в клетку, с большим масштабом. Подписываем карандашом над каждым графиком название этой функции. Подпись графиков делается исключительно ради удобства дальнейших вычислений. Получив график искомой фигуры, в большинстве случаев будет видно сразу, какие пределы интегрирования будут использованы. Таким образом мы решаем задачу графическим методом. Однако бывает так, что значения пределов дробные или иррациональные. Поэтому, можно сделать дополнительные расчеты, переходим в шагу два.

2. Если явно не заданы пределы интегрирования, то находим точки пересечения графиков друг с другом, и смотрим, совпадает ли наше графическое решение с аналитическим.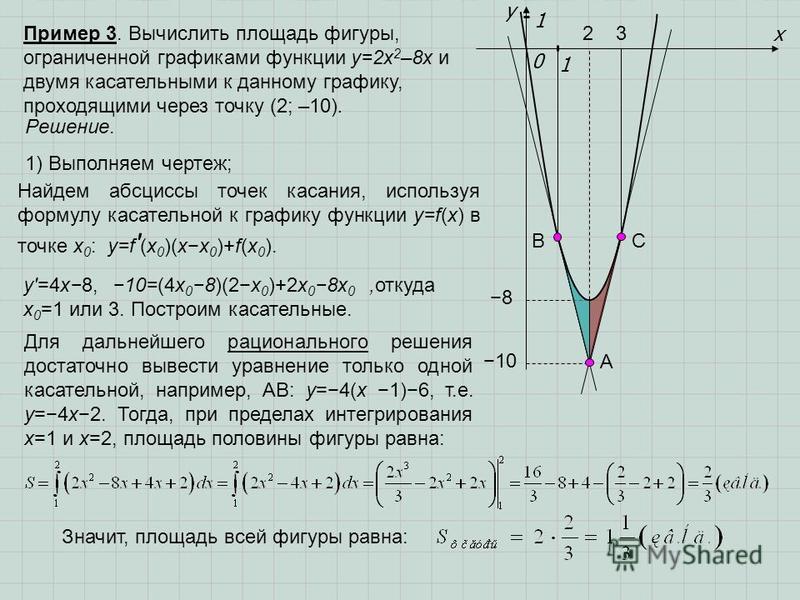

3. Далее, необходимо проанализировать чертеж. В зависимости от того, как располагаются графики функций, существуют разные подходы к нахождению площади фигуры. Рассмотрим разные примеры на нахождение площади фигуры при помощи интегралов.

3.1. Самый классический и простой вариант задачи, это когда нужно найти площадь криволинейной трапеции. Что такое криволинейная трапеция? Это плоская фигура, ограниченная осью икс ( у = 0 ), прямыми х = а, х = b и любой кривой, непрерывной на промежутке от a до b. При этом, данная фигура неотрицательна и располагается не ниже оси абсцисс. В этом случае, площадь криволинейной трапеции численно равна определенному интегралу, вычисляемого по формуле Ньютона-Лейбница:

Пример 1. Вычислить площадь фигуры, ограниченной линиями y = x2 — 3x + 3, x = 1, x = 3, y = 0.

Решение:

Какими линиями ограничена фигура? Имеем параболу y = x2 — 3x + 3

, которая располагается над осью ОХ, она неотрицательна, т. к. все точки этой параболы имеют положительные значения. Далее, заданы прямые х = 1 и х = 3, которые пролегают параллельно оси ОУ, являются ограничительными линиями фигуры слева и справа. Ну и у = 0, она же ось икс, которая ограничивает фигуру снизу. Полученная фигура заштрихована, как видно из рисунка слева. В данном случае, можно сразу приступать к решению задачи. Перед нами простой пример криволинейной трапеции, которую далее решаем с помощью формулы Ньютона-Лейбница.

3.2. В предыдущем пункте 3.1 разобран случай, когда криволинейная трапеция расположена над осью икс. Теперь рассмотрим случай, когда условия задачи такие же, за исключением того, что функция пролегает под осью икс. К стандартной формуле Ньютона-Лейбница добавляется минус. Как решать подобную задачу рассмотрим далее.

Пример 2. Вычислить площадь фигуры, ограниченной линиями y = x2 + 6x + 2, x = -4, x = -1, y = 0.

Решение:

В данном примере имеем параболу y = x2 + 6x + 2, которая берет свое начало из-под оси ОХ, прямые х = -4, х = -1, у = 0. Здесь у = 0 ограничивает искомую фигуру сверху. Прямые х = -4 и х = -1 это границы, в пределах которых будет вычисляться определенный интеграл. Принцип решения задачи на поиск площади фигуры практически полностью совпадает с примером номер 1. Единственное различие в том, что заданная функция не положительная, и все также непрерывная на промежутке [-4; -1]. Что значит не положительная? Как видно из рисунка, фигура, которая заключается в рамках заданных иксов имеет исключительно «отрицательные» координаты, что нам и требуется увидеть и помнить при решении задачи. Площадь фигуры ищем по формуле Ньютона-Лейбница, только со знаком минус в начале.

 

Статья не завершена.

2 + 2x + 4, x ∈ [0, 2].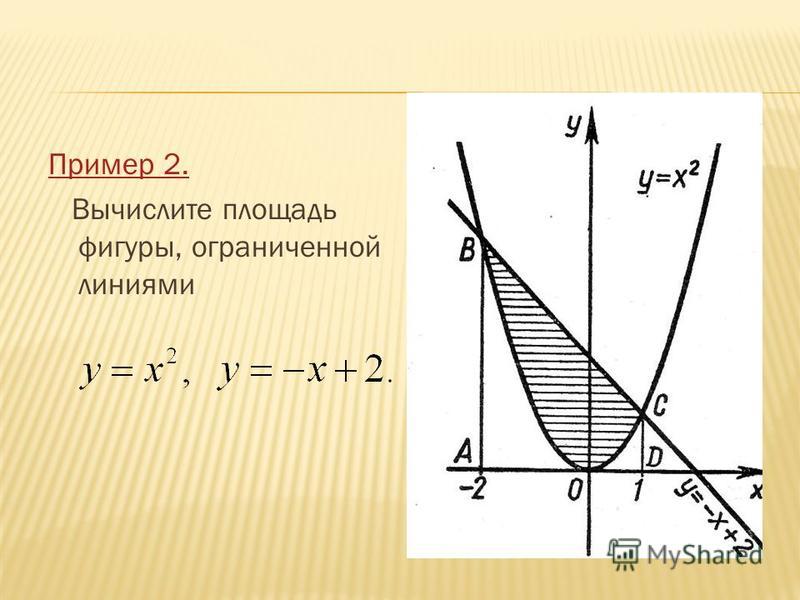 — Sarthaks eConnect

← Предыдущий вопрос Следующий вопрос →

спросил 12 декабря 2019 г. в исчислении интегралов по Абхилаша01 (37,7 тыс. баллов)

Найти площадь плоской фигуры, ограниченной y = √x, x ∈ [0, 1], y = x ² , x ∈ [1, 2] и y = –x ² + 2x + 4, х ∈ [0, 2].

• площадь, ограниченная кривыми
• джи
• электросеть

1 ответ

+1 голос

← Предыдущий вопрос Следующий вопрос →

Похожие вопросы

Площадь, ограниченная кривыми y = √x, 2y + 3 = x и осью x в первом квадранте, равна (a) 9 (b) 27/4 (c) 36 (d) 18

спросил 14 декабря 2019 г. в исчислении интегралов по Джей01 (39,6 тыс. баллов)

• площадь, ограниченная кривыми
• джи
• электросеть

Область, ограниченная кривой y = f(x) и линиями x = 0, y = 0 и x = t, лежит в интервале

спросил 14 декабря 2019 г. в исчислении интегралов по Абхилаша01 (37,7 тыс. баллов) 9х и х = 0 и х = е

спросил 14 декабря 2019 г. в исчислении интегралов по Абхилаша01 (37,7 тыс. баллов)

• площадь, ограниченная кривыми
• джи
• электросеть

Площадь области, ограниченной кривой y = f(x), осью x и линиями x = a и x = b, где – < ∞ < a < b < –2, составляет

спросил 14 декабря 2019 г. в исчислении интегралов по Абхилаша01 (37,7 тыс. баллов)

• площадь, ограниченная кривыми
• джи
• электросеть

Площадь области между кривыми y = √((1 + sin x)/cos x) и y = √((1 – sin x)/cos x), ограниченной линиями x = 0 и x = π /4 это

спросил 14 декабря 2019 г. в исчислении интегралов по Абхилаша01 (37,7 тыс. баллов)

• площадь, ограниченная кривыми
• джи
• электросеть

Категории

• Все категории
• JEE (28,1к)
  • Физика (7,5к)
  • Химия (7,5к)
  • Математика (12,1к)
    • Множества, отношения и функции (968)
    • Комплексное число и квадратные уравнения (378)
    • Матрицы и определители (112)
    • Перестановки и комбинации (139)
    • Математическая индукция (9)
    • Биномиальная теорема (330)
    • Последовательности и серии (31)
    • Предел, непрерывность и дифференцируемость (2,3к)
    • исчисление интегралов (2,1к)
    • Дифференциальные уравнения (706)
    • Координатная геометрия (387)
    • Трехмерная геометрия (412)
    • Векторная алгебра (669)
    • Статистика и вероятность (241)
    • Тригонометрия (670)
    • Математические рассуждения (5)
• NEET (8,5к)
• Наука (743к)
• Математика (241к)
• Статистика (2,8к)
• Наука об окружающей среде (3,6к)
• Биотехнология (540)
• коммерция (62,2к)
• Электроника (3,7к)
• Компьютер (15,8к)
• Искусственный интеллект (ИИ) (1,4к)
• Информационные технологии (13,2к)
• Программирование (8.

  No related posts.