Найти площадь треугольника по координатам его вершин онлайн с решением: Площадь треугольника онлайн

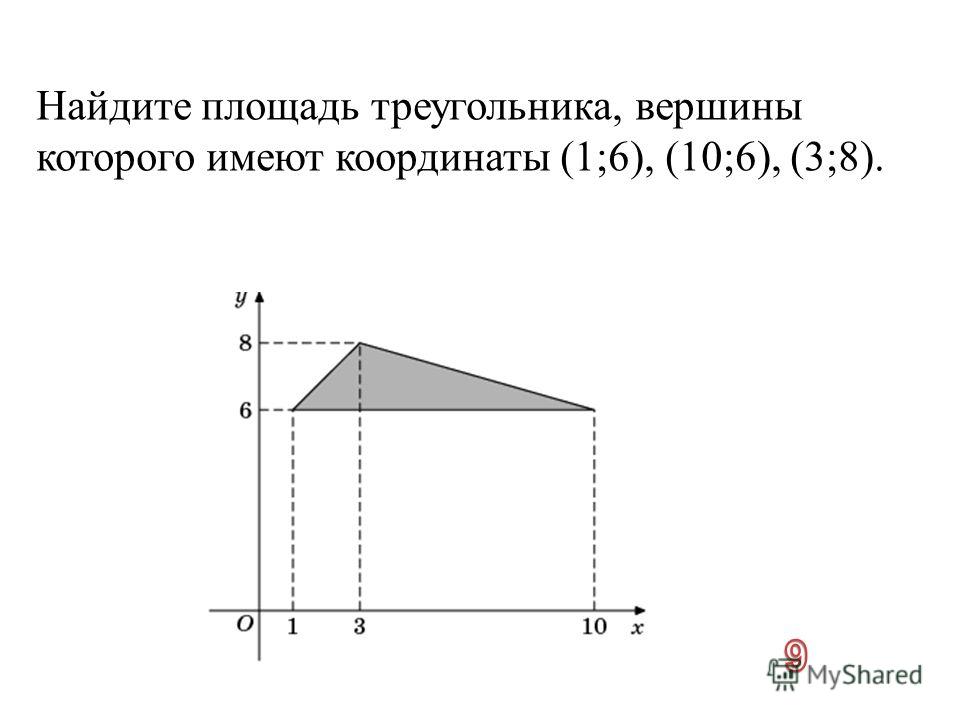
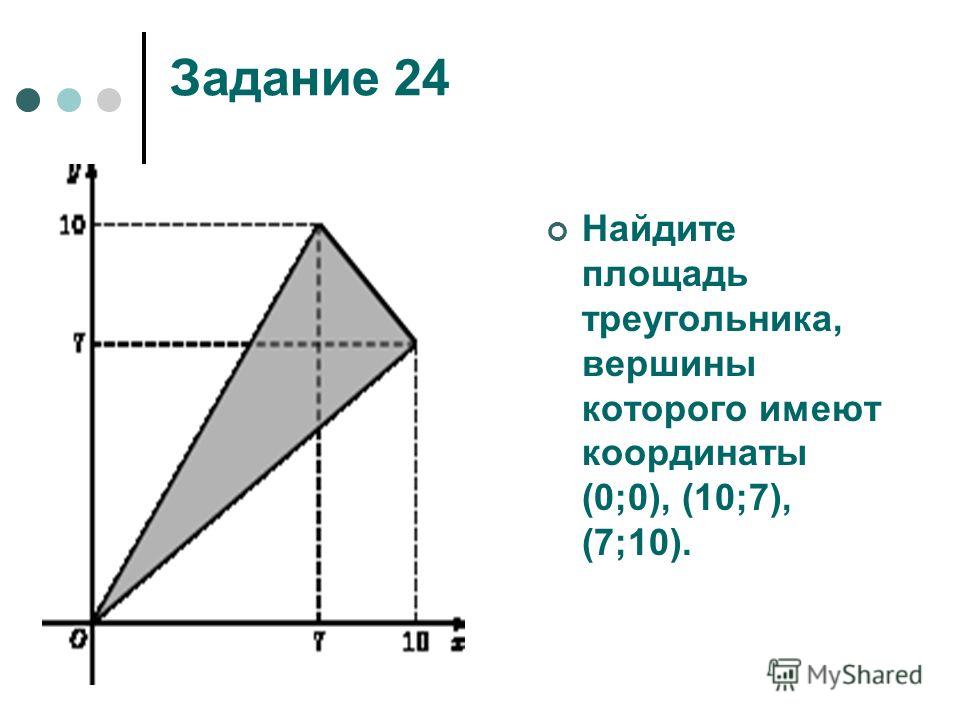
вершины треугольника имеют координаты найти площадь треугольника

Вы искали вершины треугольника имеют координаты найти площадь треугольника? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить площадь треугольника abc если известны координаты его вершин, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вершины треугольника имеют координаты найти площадь треугольника».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает.

Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вершины треугольника имеют координаты найти площадь треугольника,вычислить площадь треугольника abc если известны координаты его вершин,вычислить площадь треугольника с вершинами,даны точки вычислить площадь треугольника,как найти площадь треугольника если известны координаты вершин треугольника,как найти площадь треугольника если известны координаты его вершин,как найти площадь треугольника зная его координаты вершин,как найти площадь треугольника зная координаты его вершин,как найти площадь треугольника по координатам,как найти площадь треугольника по координатам его вершин,как по координатам найти площадь треугольника,найдите площадь треугольника с вершинами в точках,найти площадь треугольника по координатам,найти площадь треугольника по координатам его вершин,найти площадь треугольника по координатам его вершин онлайн с решением,найти площадь треугольника с вершинами,найти площадь треугольника с вершинами в точках,площадь по вершинам треугольника,площадь треугольника в пространстве по координатам вершин,площадь треугольника в пространстве через координаты вершин,площадь треугольника на плоскости,площадь треугольника онлайн по координатам вершин,площадь треугольника по вершинам,площадь треугольника по координатам,площадь треугольника по координатам вершин,площадь треугольника по координатам вершин x y z,площадь треугольника по координатам вершин в пространстве,площадь треугольника по трем точкам,площадь треугольника через координаты,площадь треугольника через координаты вершин,площадь треугольника через координаты вершин в пространстве,по координатам найти площадь треугольника,формула площади треугольника по координатам. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вершины треугольника имеют координаты найти площадь треугольника. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить площадь треугольника с вершинами).

Где можно решить любую задачу по математике, а так же вершины треугольника имеют координаты найти площадь треугольника Онлайн?

Решить задачу вершины треугольника имеют координаты найти площадь треугольника вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Вычисление площади многоугольника — презентация онлайн

1. Вычисление площади многоугольника

Городская научно-практическая конференция юных исследователей
«Будущее Петрозаводска»
Вычисление площади
многоугольника
Качановская Алина Игоревна
МОУ «Гимназия №30 имени Музалева Д.Н.»,
9Б класс, г. Петрозаводск.
Руководитель Орлова Ирина Анатольевна
учитель математики
МОУ «Гимназия №30 имени Музалева Д.Н.»

2. Вычисление площади многоугольника

Гипотеза.
Используя координатный метод и формулу Пика, можно сократить время
для вычисления площади многоугольника.
Объект исследования – площадь многоугольника.
Предмет исследования – способы нахождения площади многоугольника.
Цель исследования: изучить методы вычисления площади по координатам
вершин и с помощью формулы Пика и научиться применять их на практике.
Задачи:
• изучить теоретический материал по данной теме;
• вывести формулы вычисления площади по координатам;
• на практике применить данные способы для вычисления площадей
многоугольников;
• сравнить результаты нахождения площади многоугольников разными
способами.
Методы исследования: изучение литературы и Интернет-ресурсов,
сравнение, обобщение, аналогия.

3. Вычисление площади многоугольника по координатам его вершин

Найти площадь пятиугольника АВСDE с вершинами:
А(5;7), В(1;1), С(- 4; 2), D(- 1; — 4), Е(4; — 3).
х
у
А
5
7
В
1
1
С
-4
2
D
-1
-4
Е
4
-3
А
5
7
1) Абсциссу 1 точки умножаем на
ординату 2 точки, абсциссу 2 точки — на
ординату 3 точки и так далее.
Складываем произведения:
5 ∙ 1 + 1 ∙ 2 + (-4) ∙ (-4) + (-1) ∙ (- 3) + 4∙7 = 54.
2) Ординату 1 точки умножаем на абсциссу
2 точки, ординату 2 точки — на абсциссу 3
точки и так далее.
Складываем произведения:
7 ∙ 1 + 1 ∙ (-4) + 2 ∙ (-1) + (-4) ∙ 4 + (- 3) ∙5 = — 30.
3) Из первой суммы вычитаем вторую: 54 – (- 30) = 84.
4) Полученную сумму делим на 2: 84 : 2 = 42.
SABCDE = 42 кв. ед.

4. Вычисление площади треугольника

х
у
А1
х1
у1
А2
х2
у2
А3
х3
у3
А1
х1
у1
Треугольник А1А2А3 с координатами
вершин (х1, у1), (х2,у2) и (х3, у3).
S 0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 )
Равенство 1

5. Вычисление площади треугольника

.
S A1 A2 A3 S A2 A1B1B2 S A2 A3 B3 B2 S A3 A1B1B3
(равенство 2)
Так как А1А2В2В1 трапеция, то
S = 0,5(А2В2 + А1В1) ∙ В2В1
S A2 A1B1B2 0,5 y2 y1 x1 x2 .
S A2 A3 B3 B2 0,5 y 2 y 3 x3 x 2 и
S A3 A1B1B3 0,5 y3 y1 x1 x3 .
Выполним алгебраические преобразования
S А1 А2 А3 0,5 у 2 у1 х1 х 2 0,5 у 2 у3 х3 х 2 0,5 у1 у 3 х1 х3
0,5 у 2 х1 0,5 у 2 х2 0,5 у1 х1 0,5 у1 х2 0,5 у 2 х3 0,5 у 2 х2 0,5 у3 х3 0,5 у3 х2 0,5 у3 х1
0,5 у3 х3 0,5 у1 х1 0,5х3 у1 0,5 х1 у 2 х2 у3 х3 у1 0,5 у1 х2 у 2 х3 у3 х1
0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 ) .

6. Вычисление площади треугольника

.
S A1 A2 A3 S A2 A3 B3 B2 S A2 A1B1B2 S A1 A3 B3 B1
(равенство 3)
S A2 A3 B3 B2 0,5 y 2 y 3 x3 x 2
S A2 A1B1B2 0,5 y 2 y1 x1 x 2
S A3 A1B1B3 0,5 y 3 y1 x3 x1
Выполним алгебраические преобразования
S А1 А2 А3 0,5 у 2 у3 х3 х 2 0,5 у 2 у1 х1 х 2 0,5 у1 у 3 х3 х1
0,5 у 2 х3 0,5 у 2 х2 0,5 у3 х3 0,5 у3 х2 0,5 у 2 х1 0,5 у 2 х2 0,5 у1 х1 0,5 у1 х2 0,5 у1 х3
0,5 у1 х1 0,5 у3 х3 0,5х1 у3 0,5 х1 у 2 х2 у3 х3 у1 0,5 у1 х2 у 2 х3 у3 х1
0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 ) .

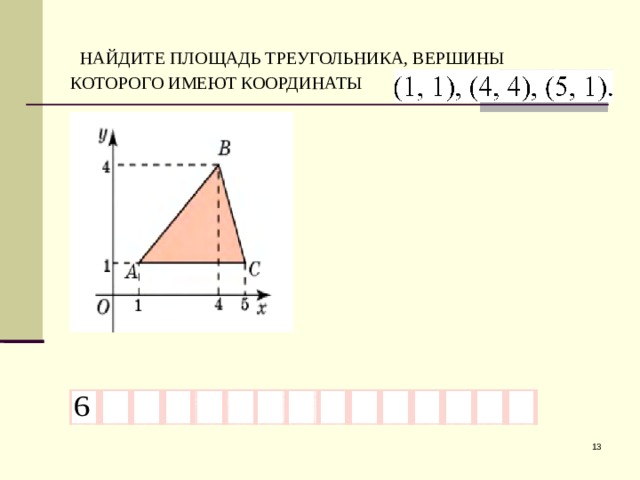
7. Вычисление площади треугольника

Если вершины треугольника взяты против часовой стрелки, то
S 0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 ) .
Если вершины треугольника взяты по часовой стрелке, то
S 0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 ) .
S 0,5 | x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 |

8. ΔАВС, А(- 3; 2), В(4,5; 0,8), С(1,8; -3,5)

А
х
у
А
-3
2
С
4,5
0,8
В
1,8
-3,5
А
-3
2
В
С
S=0,5((-3∙0,8+4,5∙(-3,5)+(1,8∙2)) –
– (2∙4,5+0,8∙1,8+(-3,5) ∙(-3))=17,745

9. Вычисление площади четырехугольника

.
S A1 A2 A3 А4 S A1 A2 А4 S A2 A3 А4
S А1 А2 А4 0,5 ( x1 y 2 x 2 y 4 x 4 y1 y1 x 2 y 2 x 4 y 4 x1 )
S А2 А3 А4 0,5 ( x 2 y3 x3 y 4 x 4 y 2 y 2 x3 y 3 x 4 y 4 x 2 )
Выполним алгебраические преобразования
S A1 A2 A3 А4 0,5 х1 у 2 0,5 х 2 у 4 0,5 х 4 у1 0,5 у1 х 2 0,5 у 2 х 4 0,5 у 4 х1 0,5 х 2 у3 0,5 х3 у 4
0,5х4 у 2 0,5 у 2 х3 0,5 у3 х4 0,5 у 4 х2 0,5( х1 у 2 х2 у3 х3 у 4 х4 у1 ) 0,5( у1 х2 у 2 х3
у3 х4 у 4 х1 )
S 0,5 ( x1 y 2 x2 y3 x3 y 4 х4 у1 y1 x2 y 2 x3 y3 x4 у 4 х1 )

10.

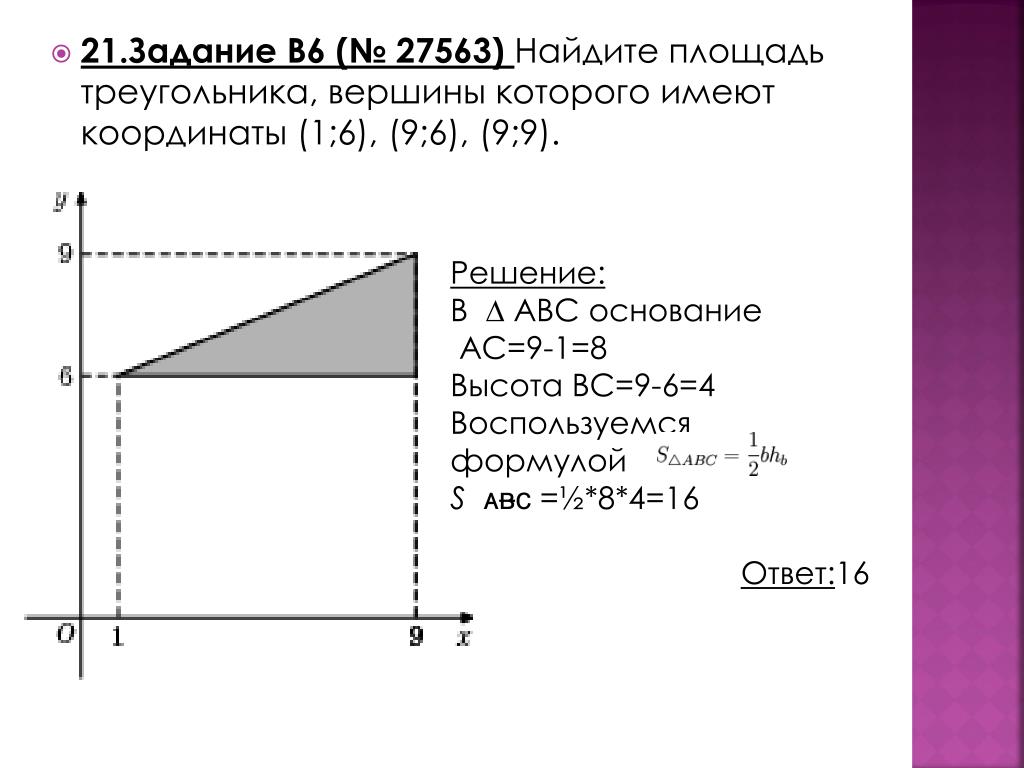МКРN, М(2; 4), К(-2,2; 0),Р(-2; 5,3), N(3;7)М
N
К
Р
S = 0,5((2∙0+(-2,2) ∙5,3+(-2) ∙7+3 ∙4) –
– (4∙(-2,2)+0∙(-2)+5,3 ∙3+7 ∙2) = 17,38
x
y
M
2
4
K
-2,2
0
P
-2
5,3
N
3
7
М
2
4

11. Алгоритм вычисления площади много- угольника по координатам его вершин

Алгоритм вычисления площади многоугольника по координатам его вершин
х
у
А1
х1
у1
1). Составить таблицу (вершины – против часовой
стрелки).
А2
х2
у2
2). Выполнить вычисления по схеме:
…
…
…
Аn
хn
уn
А1
х1
у1
1. Считаем сумму произведений координат,
соединенных стрелками, направленными от
левого верхнего угла к правому нижнему.
2. Считаем сумму произведений координат,
соединенных стрелками, направленными от
правого верхнего угла к левому нижнему.
3. От первой суммы вычитаем вторую сумму
и результат делим пополам.
S 0,5 x1 y2 x2 y3 . .. xn y1 y1 x2 y2 x3 … yn x1 .

12. АВСDE, А(-2,4; 3), В(1,2; 0,4), С(-1,5; -4), D(-5; -4), Е(-6,2; 1,4)

А
Е
В
D
С
S=0,5((-2,4)∙1,4+(-6,2) ∙(-4) ∙(-5) ∙(-4)+
+(-1,5) ∙ 0,4+1,2∙3) – (3 ∙(6,2)+1,4 ∙(-5)+
+(-4) ∙(-1,5)+(-4)∙1,2+0,4 ∙(-2,4)) = 34,9
х
у
А
-2,4
3
Е
-6,2
1,4
D
-5
-4
С
-1,5
-4
В
1,2
0,4
А
-2,4
3

13. Вычисление площади многоугольников по формуле Пика

Площадь многоугольника, изображенного на
клетчатой бумаге:
Г
S В 1
2
Георг Пик
(1859 – 1942)
Г – количество целочисленных точек на границе
многоугольника,
В – количество целочисленных точек внутри
многоугольника.

14. Вычисление площади многоугольников по формуле Пика

1
2
Г = 6, В = 26.
S = 6 : 2 + 26 – 1 = 28 (кв. ед.)
Г = 10,
В = 36.
S = 10 : 2 + 36 – 1 = 40 (кв. ед.)

15. Вычисление площади многоугольников разными способами

Площадь треугольника АВС
• Достраивание
• По формуле Пика
• По координатам вершин
S = 20 кв. ед.

16. Вычисление площади многоугольников разными способами

Площадь выпуклого
четырехугольника АВСD
• Достраивание
• По формуле Пика
• По координатам вершин
• Разбиение
S = 40 кв. ед.

17. Вычисление площади многоугольников разными способами

Площадь невыпуклого
четырехугольника АВСD
• Достраивание
• По формуле Пика
• Разбиение
• По координатам его вершин
S = 15 кв. ед.

18. Вычисление площади многоугольников разными способами

Площадь невыпуклого
семиугольника АВСDЕКМ
• Достраивание
• По формуле Пика
• По координатам его вершин
S = 47,5 кв. ед.

19. Вычисление площади многоугольника

• Представлены два способа вычисления площади многоугольника:
по координатам его вершин и по формуле Пика.
• Выведена формула для вычисления площади треугольника по
координатам его вершин.
• Выведена формула для вычисления площади четырехугольника по
координатам его вершин.
• Приведены примеры вычисления площадей многоугольников по
координатам их вершин.
• Приведены примеры вычисления площадей многоугольников по
формуле Пика.
• Приведены примеры вычисления площади одного и того же
многоугольника разными способами.

20. Вычисление площади многоугольника

Городская научно-практическая конференция юных исследователей
«Будущее Петрозаводска»
Вычисление площади
многоугольника
Качановская Алина Игоревна
МОУ «Гимназия №30 имени Музалева Д.Н.»,
9Б класс, г. Петрозаводск.
Руководитель Орлова Ирина Анатольевна
учитель математики
МОУ «Гимназия №30 имени Музалева Д.Н.»

Исчисление

— Найдите формулу площади треугольника с вершинами (в полярных координатах) $(r_1,\theta_1)$, $(r_2, \theta_2)$ и $(r_3,\theta_3)$.

спросил 1 год, 3 месяца назад

Изменено 1 год, 3 месяца назад

Просмотрено 982 раза

$\begingroup$

Я не знаю, с чего начать эту домашнюю задачу. Если бы кто-нибудь мог помочь мне начать или предоставить решение, это было бы очень признательно.

• исчисление
• полярные координаты

$\endgroup$

2

$\begingroup$

Преобразование в декартовы координаты не требуется.

Пусть вершинами треугольника будут $A,B$ и $C$ с полярными координатами, как показано ниже.

Затем используйте следующую формулу для площади треугольника, длины сторон которого равны $a$ и $b$, а включает угла между ними, равного $\theta$ $$\text{area}=\frac{1}{2}ab \sin \theta .$$

С этим

1. площадь $\треугольника ADB=\frac{1}{2}(|AD |\,|BD|) \sin (\angle ADB)=\frac{1}{2}|r_1r_2| \sin\left(\theta_2-\theta_1\right)$.
2. площадь $\треугольника BDC=\frac{1}{2}|r_2r_3| \sin\left(\theta_3-\theta_2\right)$.
3. площадь $\triangle ADC=\frac{1}{2}|r_1r_3| \sin\left(\theta_3-\theta_1\right)$.

Теперь площадь $\треугольника ABC=\треугольника ADB+\треугольника BDC-\треугольника ADC$. Так $$\text{Площадь} \triangle ABC=\color{пурпурный}{\frac{1}{2}\left[|r_1r_2| \sin\left(\theta_2-\theta_1\right)+|r_2r_3| \sin\left(\theta_3-\theta_2\right)-|r_1r_3| \sin\left(\theta_3-\theta_1\right)\right]}$$

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Нахождение площади треугольника с использованием координат

В геометрии треугольник — это трехсторонний многоугольник, который имеет 3 ребра и 3 вершины.

Площадь треугольника — это мера площади треугольника в двумерной плоскости.

В этой статье вы узнаете, как найти площадь треугольника в координатной геометрии.

Нахождение площади треугольника с использованием координат:

Когда у нас есть вершины треугольника и нам нужно найти площадь треугольника, мы можем использовать следующие шаги.

(i) Нанесите точки на грубую диаграмму.

(ii) Возьмите вершины в направлении против часовой стрелки. В противном случае формула дает отрицательное значение.

(iii) Используйте формулу, приведенную ниже

Также добавьте диагональные продукты x ₂ y ₁ , x ₃ y ₂  и x ₁ y ₃  как показано пунктирными стрелками.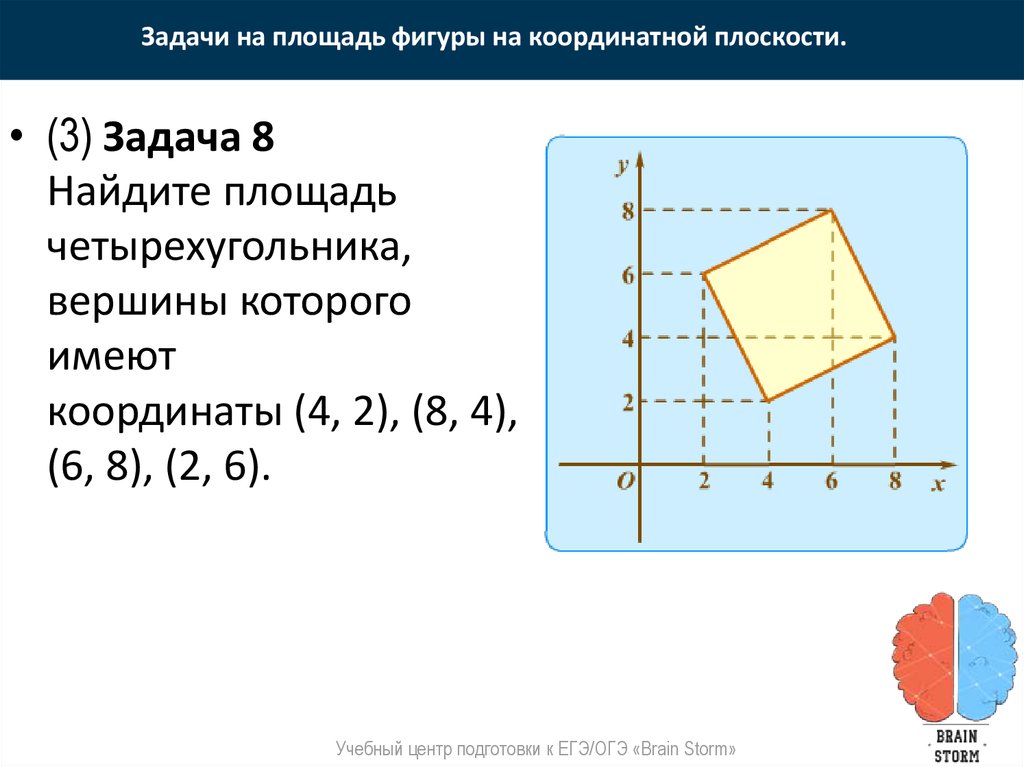

Теперь вычтите второе произведение из первого, чтобы получить площадь треугольника ABC.

Итак, площадь треугольника ABC равна

Пример 1 :

Найдите площадь треугольника с вершинами (-3, -9), (-1, 6) и (3, 9).

Решение:

Сначала мы должны нанести точку на график, как показано ниже.

Теперь нам нужно двигаться против часовой стрелки. Итак, мы должны взять точки в порядке C (3, 9) B (-1, 6) и A (-3, -9)

Площадь треугольника CBA

  =  (1/2) {(18 + 9 — 18) — (-9 — 18 — 27)}

  =  (1/2) {9 — (-54)}

  =  (1/2) {9 + 54}

  =  (1/2) (63)

  =  (63/2) 

  =  31,5 квадратных единиц.

Следовательно, площадь ЗДВ = 31,5 кв.

Пример 2 :

Найдите площадь треугольника с вершинами (-3, -9), (3, 9) и (5, -8).

Решение:

Сначала мы должны нанести точку на график, как показано ниже.

Теперь нам нужно двигаться против часовой стрелки. Таким образом, мы должны взять точки в порядке B (3, 9) A (-3, -9) и C (5, -8)

x ₁   =  3     x ₂   =  -3      x ₃ = 5

Y ₁ = 9 Y ₂ = -9 Y ₃ = -8

Область треугольника BAC

= (1/2) {(-27 -24 + 45) — (-27 — 45 — 24)}

  =  (1/2) {(-51 + 45) — (-96)}

  =  (1/2) {-6 + 96}

  =  (1/2) (90)

  = (90/2)

 =  45 квадратных единиц.

Следовательно, площадь BAC = 45 квадратных единиц.

Пример 3 :

Найдите площадь треугольника с вершинами (4, 5) (4, 2) и (-2, 2).

Решение:

Теперь нам нужно двигаться против часовой стрелки. Итак, мы должны взять точки в порядке A (4, 5) C (-2, 2) и B (4, 2)

x ₁ = 4 x ₂ = -2 x ₃ = 4

y ₁ = 5 Y ₂ = 2 y ₃ = 2

Область Triangle ACB

999 3 = 2

Область Triangle ACB 9000

2 = 2

. = (1/2) {(8 — 4 + 20) — (-10 + 8 + 8)}

  =  (1/2) {(28 — 4) — (-10 + 16)}

  = (1/2) (24 — 6)

  =  (1/2) x 18

  =  (18/2) 

  =  9 кв.

Следовательно, площадь ACB = 9квадратные единицы

Пример 4 :

Найдите площадь треугольника с вершинами (3, 1) (2, 2) и (2, 0).

Решение:

Теперь нам нужно двигаться против часовой стрелки. Таким образом, мы должны взять точки в порядке B (2, 2) C (2, 0) и A (3, 1)

x ₁   =  2       x ₂   = 2       x ₃   = 3

y ₁   =  2       y ₂  = 0       y ₃   =  1

Площадь треугольника BCA 

  =  (1/2) {(0 + 2 + 6) — (4 + 0 + 2)}

  =  (1/2) {8 — 6}

  =  ( 1/2) (2)

  =  (2/2)

  =  1 кв.

Следовательно, площадь ACB = 1 кв.

Пример 5 :

Найдите площадь треугольника с вершинами (3, 1), (0, 4) и (-3, 1).